26.2: Tasas de migración de solutos

Nuestra capacidad para separar dos solutos depende de las interacciones de equilibrio del soluto con la fase estacionaria y la fase móvil, lo que afecta tanto el tiempo que tarda un soluto en viajar por la columna como el ancho del perfil de elución del soluto. En esta sección consideramos la velocidad a la que el soluto se mueve a través de la columna.

Constantes de Distribución

Supongamos que podemos describir la distribución de un soluto entre la fase móvil y la fase estacionaria usando la siguiente reacción de equilibrio

\[S_{\text{m}} \rightleftharpoons S_{\text{s}} \label{mig1} \]

donde S _m es el soluto en la fase móvil y S _s es el soluto en la fase estacionaria. La constante de equilibrio para esta reacción es un coeficiente de partición de equilibrio, K _D.

\[K_{D}=\frac{\left[S_{\mathrm{s}}\right]}{\left[S_\text{m}\right]} \label{mig2} \]

Esto no es una suposición trivial. En esta sección estamos, en efecto, tratando el equilibrio del soluto entre la fase móvil y la fase estacionaria como si fuera idéntico al equilibrio en una extracción líquido-líquido. Podría cuestionarse si se trata de una suposición razonable. Hay una diferencia importante entre los dos experimentos que debemos considerar. En una extracción líquido-líquido, que se realiza en un embudo separador, las dos fases permanecen en contacto entre sí en todo momento, permitiendo un verdadero equilibrio. En cromatografía, sin embargo, la fase móvil está en constante movimiento. Un soluto que se mueve a la fase estacionaria desde la fase móvil se equilibrará de nuevo en una porción diferente de la fase móvil; esto no describe un verdadero equilibrio.

Entonces, preguntamos nuevamente: ¿Podemos tratar la distribución de un soluto entre la fase móvil y la fase estacionaria como un proceso de equilibrio? La respuesta es sí, si la velocidad de la fase móvil es lenta en relación con la cinética del movimiento del soluto de ida y vuelta entre las dos fases. En general, esta es una suposición razonable.

Tiempo de Retención

Podemos caracterizar las propiedades de un pico cromatográfico de varias maneras, dos de las cuales se muestran en la Figura\(\PageIndex{1}\). El tiempo de retención, t _r, es el tiempo entre la inyección de la muestra y la respuesta máxima para el pico del soluto. El ancho basal de un pico cromatográfico, w, como se muestra en la Figura\(\PageIndex{1}\), se determina extendiendo las líneas tangentes desde los puntos de inflexión a ambos lados del pico hasta la línea base. Aunque usualmente reportamos t _r y w usando unidades de tiempo, podemos reportarlos usando unidades de volumen multiplicando cada uno por la velocidad de la fase móvil, o reportarlos en unidades lineales midiendo distancias con una regla.

Por ejemplo, el volumen de retención de un soluto, V _r, es\(t_\text{r} \times u\) donde u es la velocidad de la fase móvil a través de la columna.

Figura\(\PageIndex{1}\). Cromatograma que muestra un tiempo de retención de soluto, t _r, y ancho de línea base, w, y el tiempo de vacío de la columna, t _m, para solutos no retenidos. En esta sección nos enfocamos en el tiempo de retención; consideraremos el ancho del pico del soluto en la Sección 26.3.

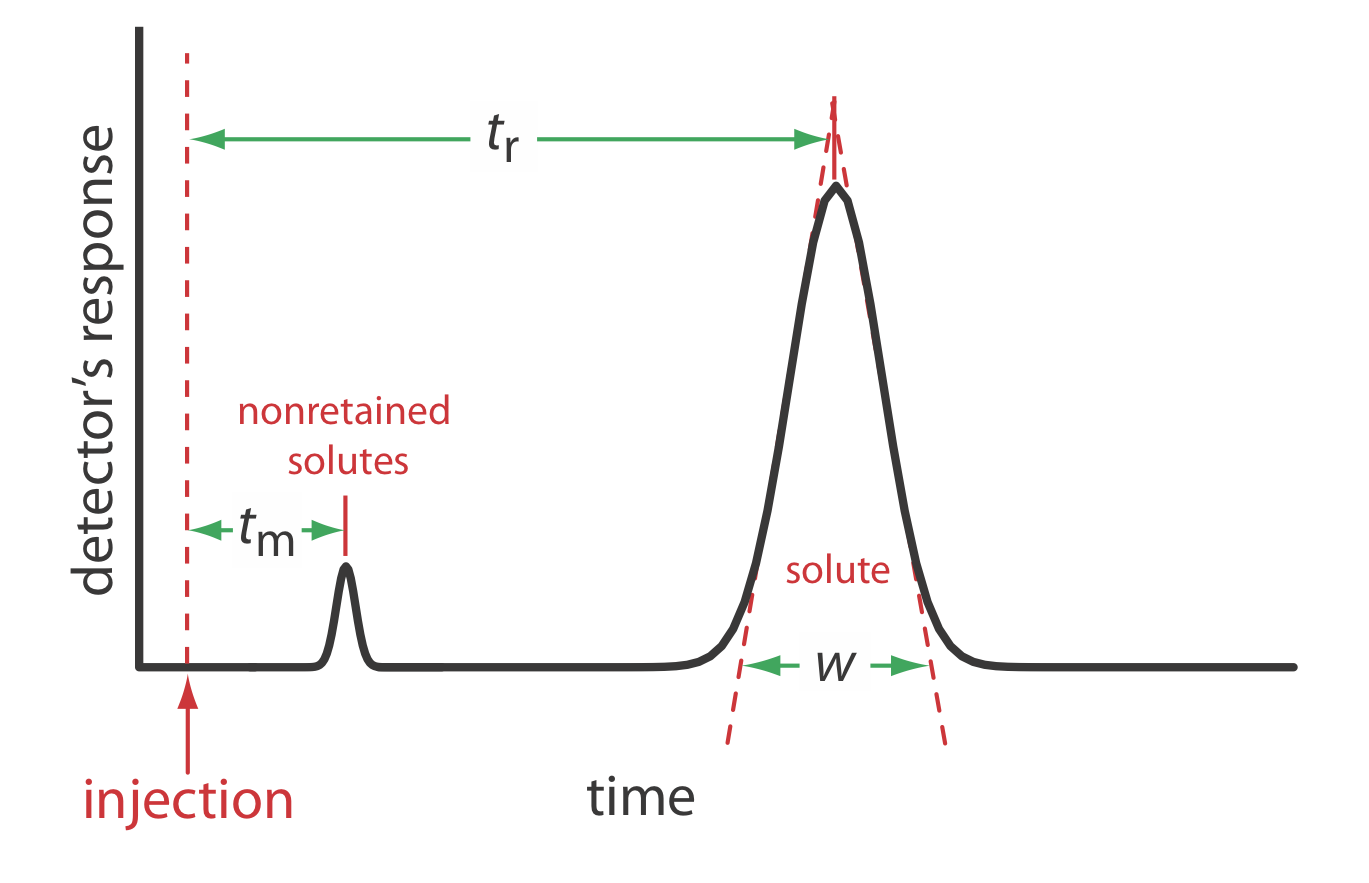
Además del pico del soluto, la Figura\(\PageIndex{1}\) también muestra un pequeño pico que eluye poco después de inyectar la muestra en la fase móvil. Este pico contiene todos los solutos no retenidos, que se mueven a través de la columna a la misma velocidad que la fase móvil. El tiempo requerido para eluir los solutos no retenidos se denomina tiempo vacío de la columna, t _m.

La tasa de migración de solutos: el factor de retención

En ausencia de cualquier reacción de equilibrio adicional en la fase móvil o la fase estacionaria, K _D es equivalente a la relación de distribución, D,

\[D=\frac{\left[S_{0}\right]}{\left[S_\text{m}\right]}=\frac{(\operatorname{mol} \text{S})_\text{s} / V_\text{s}}{(\operatorname{mol} \text{S})_\text{m} / V_\text{m}}=K_{D} \label{mig3} \]

donde V _s y V _m son los volúmenes de la fase estacionaria y la fase móvil, respectivamente.

Una conservación de la masa requiere que los moles totales de soluto permanezcan constantes a lo largo de la separación; así, sabemos que la siguiente ecuación es cierta.

\[(\operatorname{mol} \text{S})_{\operatorname{tot}}=(\operatorname{mol} \text{S})_{\mathrm{m}}+(\operatorname{mol} \text{S})_\text{s} \label{mig4} \]

Resolviendo la Ecuación\ ref {mig4} para los moles de soluto en la fase estacionaria y sustituyendo en la Ecuación\ ref {mig2} nos deja con

\[D = \frac{\left\{(\text{mol S})_{\text{tot}} - (\text{mol S})_\text{m}\right\} / V_{\mathrm{s}}}{(\text{mol S})_{\mathrm{m}} / V_{\mathrm{m}}} \label{mig5} \]

Reordenando esta ecuación y resolviendo para la fracción de soluto en la fase móvil, f _m, da

\[f_\text{m} = \frac {(\text{mol S})_\text{m}} {(\text{mol S})_\text{tot}} = \frac {V_\text{m}} {DV_\text{s} + V_\text{m}} \label{mig6} \]

Debido a que tal vez no sepamos los volúmenes exactos de la fase estacionaria y la fase móvil, simplificamos la Ecuación\ ref {mig6} dividiendo tanto el numerador como el denominador entre V _m; así

\[f_\text{m} = \frac {V_\text{m}/V_\text{m}} {DV_\text{s}/V_\text{m} + V_\text{m}/V_\text{m}} = \frac {1} {DV_\text{s}/V_\text{m} + 1} = \frac {1} {1+k} \label{mig7} \]

donde k

\[k=D \times \frac{V_\text{s}}{V_\text{m}} \label{mig8} \]

es el factor de retención del soluto. Tenga en cuenta que cuanto mayor sea el factor de retención, más favorece la relación de distribución a la fase estacionaria, lo que lleva a un soluto retenido más fuertemente y a un mayor tiempo de retención.

Otros nombres (más antiguos) para el factor de retención son factor de capacidad, relación de capacidad y relación de partición, y a veces se le da el símbolo\(k^{\prime}\). Tenga esto en cuenta si está utilizando otros recursos. El factor de retención es el nombre aprobado del Libro de Oro de la IUPAC.

Podemos determinar un factor de retención de soluto a partir de un cromatograma midiendo el tiempo de vacío de la columna, t _m, y el tiempo de retención del soluto, t _r (ver Figura\(\PageIndex{1}\)). Resolviendo la ecuación\ ref {mig7} para k, encontramos que

\[k=\frac{1-f_\text{m}}{f_\text{m}} \label{mig9} \]

Anteriormente definimos f _m como la fracción de soluto en la fase móvil. Suponiendo una velocidad de fase móvil constante, también podemos definir f _m como

\[f_\text{m}=\frac{\text { time spent in the mobile phase }}{\text { time spent in the stationary phase }}=\frac{t_\text{m}}{t_\text{r}} \label{mig10} \]

Sustituir de nuevo a la Ecuación\ ref {mig9} y reorganizar nos deja con

\[k=\frac{1-\frac{t_{m}}{t_{r}}}{\frac{t_{\mathrm{m}}}{t_{\mathrm{r}}}}=\frac{t_{\mathrm{r}}-t_{\mathrm{m}}}{t_{\mathrm{m}}}=\frac{t_{\mathrm{r}}^{\prime}}{t_{\mathrm{m}}} \label{mig11} \]

donde\(t_\text{r}^{\prime}\) está el tiempo de retención ajustado.

Ejemplo\(\PageIndex{1}\)

En un análisis cromatográfico de ácidos de bajo peso molecular, el ácido butírico eluye con un tiempo de retención de 7.63 min. El tiempo de vacío de la columna es de 0.31 min. Calcular el factor de retención para el ácido butírico.

Solución

\[k_{\mathrm{but}}=\frac{t_{\mathrm{r}}-t_{\mathrm{m}}}{t_{\mathrm{m}}}=\frac{7.63 \text{ min}-0.31 \text{ min}}{0.31 \text{ min}}=23.6 \nonumber \]

Figura\(\PageIndex{2}\). Cromatograma para Ejercicio\(\PageIndex{1}\).

Tasas de migración relativa: El factor de selectividad

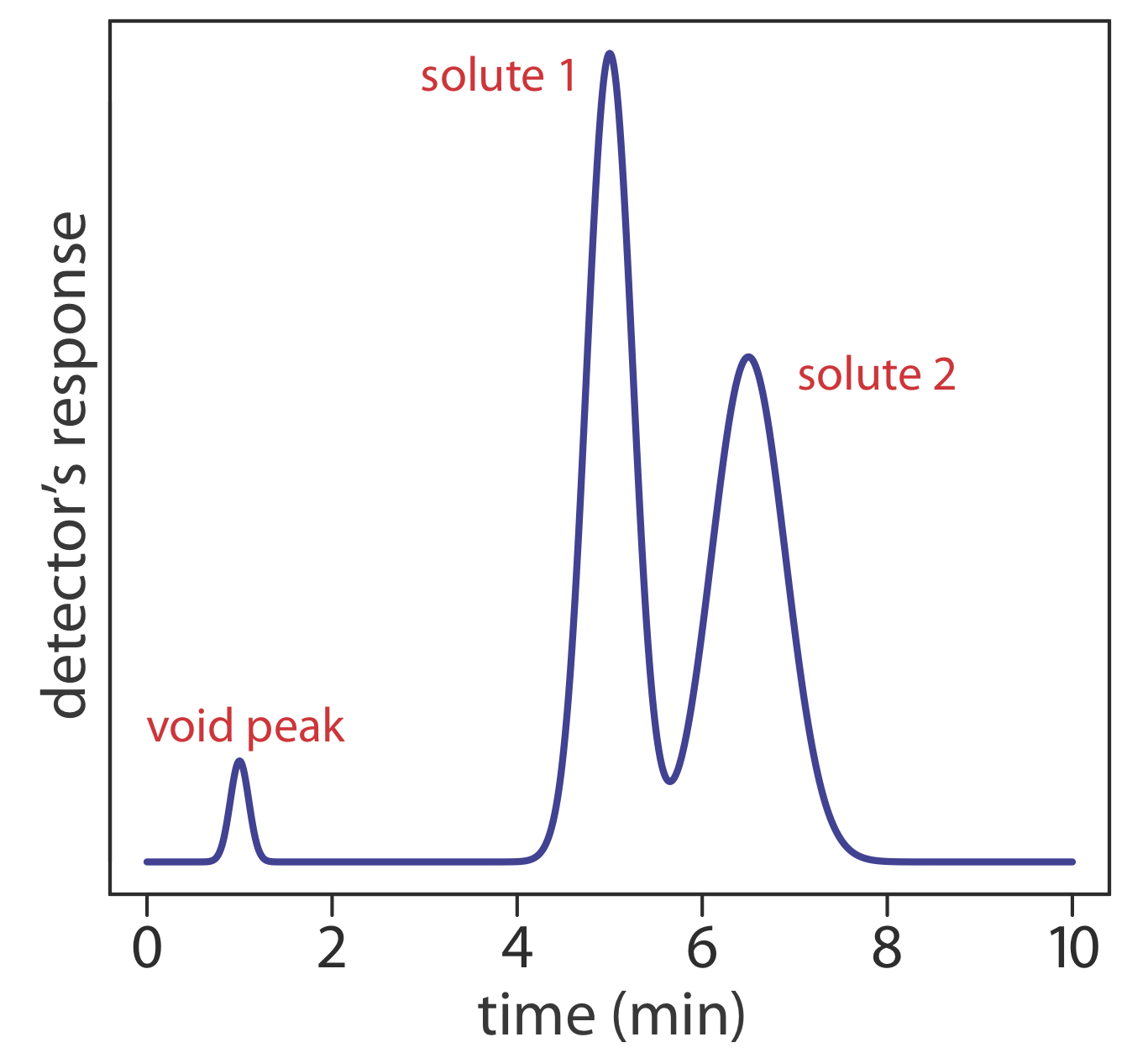
La selectividad es una medida relativa de la retención de dos solutos, que definimos usando un factor de selectividad,\(\alpha\)

\[\alpha=\frac{k_{B}}{k_{A}}=\frac{t_{r, B}-t_{\mathrm{m}}}{t_{r, A}-t_{\mathrm{m}}} \label{mig12} \]

donde el soluto A tiene el menor tiempo de retención. Cuando dos solutos eluyen con idéntico tiempo de retención,\(\alpha = 1.00\); para todas las demás condiciones\(\alpha > 1.00\).

Ejemplo\(\PageIndex{2}\)

En el análisis cromatográfico para ácidos de bajo peso molecular descrito en el Ejemplo\(\PageIndex{1}\), el tiempo de retención para el ácido isobutírico es de 5.98 min. ¿Cuál es el factor de selectividad para el ácido isobutírico y el ácido butírico?

Solución

Primero debemos calcular el factor de retención para el ácido isobutírico. Usando el tiempo vacío del Ejemplo\(\PageIndex{1}\) tenemos

\[k_{\mathrm{iso}}=\frac{t_{\mathrm{r}}-t_{\mathrm{m}}}{t_{\mathrm{m}}}=\frac{5.98 \text{ min}-0.31 \text{ min}}{0.31 \text{ min}}=18.3 \nonumber \]

El factor de selectividad, por lo tanto, es

\[\alpha=\frac{k_{\text {but }}}{k_{\text {iso }}}=\frac{23.6}{18.3}=1.29 \nonumber \]