4.6: Métodos Estadísticos para Distribuciones Normales
- Page ID
- 75495
La distribución más común para nuestros resultados es una distribución normal. Debido a que el área entre dos límites cualesquiera de una curva de distribución normal está bien definida, construir y evaluar pruebas de significancia es sencillo.
Comparando\(\overline{X}\) con\(\mu\)
Una forma de validar un nuevo método analítico es analizar una muestra que contiene una cantidad conocida de analito,\(\mu\). Para juzgar la precisión del método analizamos varias porciones de la muestra, determinamos la cantidad promedio de analito en la muestra y usamos una prueba de significancia\(\overline{X}\) para compararla\(\mu\).\(\overline{X}\) Nuestra hipótesis nula es que la diferencia entre\(\overline{X}\) y\(\mu\) se explica por errores indeterminados que afectan la determinación de\(\overline{X}\). La hipótesis alternativa es que la diferencia entre\(\overline{X}\) y\(\mu\) es demasiado grande para ser explicada por error indeterminado.
\[H_0 \text{: } \overline{X} = \mu \nonumber\]
\[H_A \text{: } \overline{X} \neq \mu \nonumber\]
El estadístico de prueba es t exp, que sustituimos en el intervalo de confianza\(\mu\) dado por la Ecuación 4.4.5
\[\mu = \overline{X} \pm \frac {t_\text{exp} s} {\sqrt{n}} \label{4.1}\]
Reordenando esta ecuación y resolviendo\(t_\text{exp}\)
\[t_\text{exp} = \frac {|\mu - \overline{X}| \sqrt{n}} {s} \label{4.2}\]
da el valor para\(t_\text{exp}\) cuando\(\mu\) está en el borde derecho o en el borde izquierdo del intervalo de confianza de la muestra (Figura 4.6.1 a)
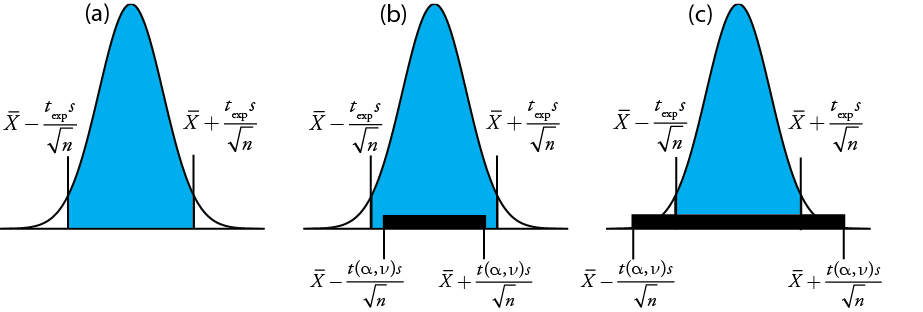
Para determinar si debemos retener o rechazar la hipótesis nula, comparamos el valor de t exp con un valor crítico,\(t(\alpha, \nu)\), donde\(\alpha\) está el nivel de confianza y\(\nu\) es los grados de libertad para la muestra. El valor crítico\(t(\alpha, \nu)\) define el mayor intervalo de confianza explicado por error indeterminado. Si\(t_\text{exp} > t(\alpha, \nu)\), entonces el intervalo de confianza de nuestra muestra es mayor que el explicado por errores indeterminados (Figura 4.6.1 b). En este caso, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Si\(t_\text{exp} \leq t(\alpha, \nu)\), entonces el intervalo de confianza de nuestra muestra es menor que el explicado por un error indeterminado, y conservamos la hipótesis nula (Figura 4.6.1 c). El ejemplo 4.6.1 proporciona una aplicación típica de esta prueba de significación, que se conoce como prueba t de\(\overline{X}\) a\(\mu\).
Encontrará valores para\(t(\alpha, \nu)\) en el Apéndice 4.
Otro nombre para la prueba t es la prueba t de Student. Estudiante fue el seudónimo de William Gossett (1876-1927) quien desarrolló la prueba t mientras trabajaba como estadístico para la cervecería Guiness en Dublín, Irlanda. Publicó bajo el nombre de Student porque la cervecería no quería que sus competidores supieran que estaban usando estadísticas para ayudar a mejorar la calidad de sus productos.
Antes de determinar la cantidad de Na 2 CO 3 en una muestra, decide verificar su procedimiento analizando una muestra estándar que es 98.76% w/w Na 2 CO 3. Cinco determinaciones replicadas del% p/p de Na 2 CO 3 en el patrón dieron los siguientes resultados
\(98.71 \% \quad 98.59 \% \quad 98.62 \% \quad 98.44 \% \quad 98.58 \%\)
Utilizando\(\alpha = 0.05\), ¿hay alguna evidencia de que el análisis está dando resultados inexactos?
Solución
La media y la desviación estándar para los cinco ensayos son
\[\overline{X} = 98.59 \quad \quad \quad s = 0.0973 \nonumber\]
Debido a que no hay razón para creer que los resultados para el estándar deben ser mayores o menores que\(\mu\), una prueba t de dos colas es apropiada. La hipótesis nula y la hipótesis alternativa son
\[H_0 \text{: } \overline{X} = \mu \quad \quad \quad H_\text{A} \text{: } \overline{X} \neq \mu \nonumber\]
El estadístico de prueba, t exp, es
\[t_\text{exp} = \frac {|\mu - \overline{X}|\sqrt{n}} {2} = \frac {|98.76 - 98.59| \sqrt{5}} {0.0973} = 3.91 \nonumber\]
El valor crítico para t (0.05, 4) del Apéndice 4 es 2.78. Dado que t exp es mayor que t (0.05, 4), rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Al nivel de confianza del 95% la diferencia entre\(\overline{X}\) y\(\mu\) es demasiado grande para ser explicada por fuentes indeterminadas de error, lo que sugiere que existe una fuente determinada de error que afecta el análisis.
Hay otra manera de interpretar el resultado de esta prueba t. Sabiendo que t exp es 3.91 y que hay 4 grados de libertad, utilizamos el Apéndice 4 para estimar el\(\alpha\) valor correspondiente a una t (\(\alpha\), 4) de 3.91. Del Apéndice 4, t (0.02, 4) es 3.75 y t (0.01, 4) es 4.60. Si bien podemos rechazar la hipótesis nula en el nivel de confianza del 98%, no podemos rechazarla en el nivel de confianza del 99%. Para una discusión sobre las ventajas de este enfoque, véase J. A. C. Sterne y G. D. Smith “Tamizar la evidencia, ¿qué hay de malo en las pruebas de significación?” BMJ 2001, 322, 226—231.
Para evaluar la precisión de un nuevo método analítico, un analista determina la pureza de un estándar para el cual\(\mu\) es 100.0%, obteniendo los siguientes resultados.
\(99.28 \% \quad 103.93 \% \quad 99.43 \% \quad 99.84 \% \quad 97.60 \% \quad 96.70 \% \quad 98.02 \%\)
¿Hay alguna evidencia de\(\alpha = 0.05\) que existe un error determinado que afecte los resultados?
- Responder
-
La hipótesis nula es\(H_0 \text{: } \overline{X} = \mu\) y la hipótesis alternativa es\(H_\text{A} \text{: } \overline{X} \neq \mu\). La media y la desviación estándar para los datos son 99.26% y 2.35%, respectivamente. El valor para t exp es
\[t_\text{exp} = \frac {|100.0 - 99.26| \sqrt{7}} {2.35} = 0.833 \nonumber\]
y el valor crítico para t (0.05, 6) es 2.477. Debido a que t exp es menor que t (0.05, 6) conservamos la hipótesis nula y no tenemos evidencia de una diferencia significativa entre\(\overline{X}\) y\(\mu\).
Anteriormente hicimos el punto de que debemos tener precaución cuando interpretamos el resultado de un análisis estadístico. Seguiremos volviendo a este punto porque es importante. Habiendo determinado que un resultado es inexacto, como hicimos en Ejemplo 4.6.1 , el siguiente paso es identificar y corregir el error. Sin embargo, antes de invertir tiempo y dinero en esto, primero debemos examinar críticamente nuestros datos. Por ejemplo, cuanto menor sea el valor de s, mayor será el valor de t exp. Si la desviación estándar para nuestro análisis es poco realista, entonces la probabilidad de un error tipo 2 aumenta. Incluir algunos análisis replicados adicionales del estándar y reevaluar la prueba t puede fortalecer nuestra evidencia de un error determinado, o puede mostrarnos que no hay evidencia de un error determinado.
Comparando\(s^2\) con\(\sigma^2\)
Si analizamos regularmente una muestra en particular, es posible que podamos establecer una varianza esperada,\(\sigma^2\), para el análisis. Este suele ser el caso, por ejemplo, en un laboratorio clínico que analiza cientos de muestras de sangre cada día. Algunos análisis replicados de una sola muestra dan una varianza muestral, s 2, cuyo valor puede o no diferir significativamente de\(\sigma^2\).
Podemos usar una prueba F para evaluar si una diferencia entre s 2 y\(\sigma^2\) es significativa. La hipótesis nula es\(H_0 \text{: } s^2 = \sigma^2\) y la hipótesis alternativa es\(H_\text{A} \text{: } s^2 \neq \sigma^2\). El estadístico de prueba para evaluar la hipótesis nula es F exp, que se da como
dependiendo de si s 2 es mayor o menor que\(\sigma^2\). Esta forma de definir F exp asegura que su valor siempre sea mayor o igual a uno.
Si la hipótesis nula es verdadera, entonces F exp debería ser igual a uno; sin embargo, debido a errores indeterminados F exp suele ser mayor que uno. Un valor crítico,\(F(\alpha, \nu_\text{num}, \nu_\text{den})\), es el mayor valor de F exp que podemos atribuir al error indeterminado dado el nivel de significancia especificado,\(\alpha\), y los grados de libertad para la varianza en el numerador,\(\nu_\text{num}\), y la varianza en el denominador,\(\nu_\text{den}\). Los grados de libertad para s 2 es n — 1, donde n es el número de réplicas utilizadas para determinar la varianza de la muestra, y los grados de libertad para\(\sigma^2\) se define como infinito,\(\infty\). Los valores críticos de F para\(\alpha = 0.05\) se enumeran en el Apéndice 5 para las pruebas F de una cola y dos colas.
El proceso de un fabricante para analizar tabletas de aspirina tiene una varianza conocida de 25. Se selecciona una muestra de 10 comprimidos de aspirina y se analiza la cantidad de aspirina, dando los siguientes resultados en mg de aspirina/comprimido.
\(254 \quad 249 \quad 252 \quad 252 \quad 249 \quad 249 \quad 250 \quad 247 \quad 251 \quad 252\)
Determinar si hay evidencia de una diferencia significativa entre la varianza de la muestra y la varianza esperada en\(\alpha = 0.05\).
Solución
La varianza para la muestra de 10 comprimidos es de 4.3. La hipótesis nula y las hipótesis alternativas son
\[H_0 \text{: } s^2 = \sigma^2 \quad \quad \quad H_\text{A} \text{: } s^2 \neq \sigma^2 \nonumber\]
y el valor para F exp es
\[F_\text{exp} = \frac {\sigma^2} {s^2} = \frac {25} {4.3} = 5.8 \nonumber\]
El valor crítico para F (0.05,\(\infty\), 9) del Apéndice 5 es 3.333. Dado que F exp es mayor que F (0.05,\(\infty\), 9), rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que existe una diferencia significativa entre la varianza de la muestra y la varianza esperada. Una explicación de la diferencia podría ser que las tabletas de aspirina no se seleccionaron al azar.
Comparación de varianzas para dos muestras
Podemos extender la prueba F para comparar las varianzas para dos muestras, A y B, reescribiendo la Ecuación\ ref {4.3} como
\[F_\text{exp} = \frac {s_A^2} {s_B^2} \nonumber\]
definiendo A y B de manera que el valor de F exp sea mayor o igual a 1.
En el Cuadro 4.4.1 se muestran los resultados de dos experimentos para determinar la masa de un centavo circulante de EE.UU. Determinar si existe una diferencia en las varianzas de estos análisis en\(\alpha = 0.05\).
Solución
Las desviaciones estándar para los dos experimentos son 0.051 para el primer experimento (A) y 0.037 para el segundo experimento (B). Las hipótesis nulas y alternativas son
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_\text{A} \text{: } s_A^2 \neq s_B^2 \nonumber\]
y el valor de F exp es
\[F_\text{exp} = \frac {s_A^2} {s_B^2} = \frac {(0.051)^2} {(0.037)^2} = \frac {0.00260} {0.00137} = 1.90 \nonumber\]
Del Apéndice 5, el valor crítico para F (0.05, 6, 4) es 9.197. Debido a que F exp < F (0.05, 6, 4), conservamos la hipótesis nula. No hay evidencia que sugiera\(\alpha = 0.05\) que la diferencia en las varianzas sea significativa.
Para comparar dos lotes de producción de comprimidos de aspirina, recolectamos y analizamos muestras de cada uno, obteniendo los siguientes resultados (en mg de aspirina/tableta).
Lote 1:\(256 \quad 248 \quad 245 \quad 245 \quad 244 \quad 248 \quad 261\)
Lote 2:\(241 \quad 258 \quad 241 \quad 244 \quad 256 \quad 254\)
¿Hay alguna evidencia de\(\alpha = 0.05\) que existe una diferencia significativa en las varianzas para estas dos muestras?
- Responder
-
Las desviaciones estándar son 6.451 mg para el Lote 1 y 7.849 mg para el Lote 2. Las hipótesis nulas y alternativas son
\[H_0 \text{: } s_\text{Lot 1}^2 = s_\text{Lot 2}^2 \quad \quad \quad H_\text{A} \text{: } s_\text{Lot 1}^2 \neq s_\text{Lot 2}^2 \nonumber\]
y el valor de F exp es
\[F_\text{exp} = \frac {(7.849)^2} {(6.451)^2} = 1.480 \nonumber\]
El valor crítico para F (0.05, 5, 6) es 5.988. Debido a que F exp < F (0.05, 5, 6), conservamos la hipótesis nula. No hay evidencia que sugiera\(\alpha = 0.05\) que la diferencia en las varianzas sea significativa.
Comparación de medias para dos muestras
Tres factores influyen en el resultado de un análisis: el método, la muestra y el analista. Podemos estudiar la influencia de estos factores mediante la realización de experimentos en los que cambiamos un factor mientras mantenemos constantes los otros factores. Por ejemplo, para comparar dos métodos analíticos podemos hacer que el mismo analista aplique cada método a la misma muestra y luego examine las medias resultantes. De manera similar, podemos diseñar experimentos para comparar dos analistas o comparar dos muestras.
También es posible diseñar experimentos en los que variemos más de uno de estos factores. Volveremos a este punto en el Capítulo 14.
Antes de considerar las pruebas de significancia para comparar las medias de dos muestras, necesitamos hacer una distinción entre datos desapareados y datos pareados. Esta es una distinción crítica y aprender a distinguir entre estos dos tipos de datos es importante. Aquí hay dos ejemplos simples que resaltan la diferencia entre los datos no emparejados y los datos emparejados. En cada ejemplo el objetivo es comparar dos balanzas pesando centavos.
- Ejemplo 1: Recolectamos 10 centavos y pesamos cada centavo en cada saldo. Este es un ejemplo de datos emparejados porque usamos los mismos 10 centavos para evaluar cada saldo.
- Ejemplo 2: Recolectamos 10 centavos y los dividimos en dos grupos de cinco centavos cada uno. Pesamos los centavos en el primer grupo en una balanza y pesamos el segundo grupo de centavos en la otra balanza. Tenga en cuenta que no se pesa ningún centavo en ambas balanzas. Este es un ejemplo de datos no emparejados porque evaluamos cada saldo usando una muestra diferente de centavos.
En ambos ejemplos se extrajeron muestras de 10 centavos de una misma población; la diferencia es cómo muestreamos esa población. Aprenderemos por qué esta distinción es importante cuando revisamos la prueba de significancia para datos pareados; primero, sin embargo, presentamos la prueba de significancia para datos no apareados.
Una prueba simple para determinar si los datos están emparejados o no emparejados es observar el tamaño de cada muestra. Si las muestras son de diferente tamaño, entonces los datos deben estar desapareados. Lo contrario no es cierto. Si dos muestras son de igual tamaño, pueden estar emparejadas o desapareadas.
Datos no emparejados
Considera dos análisis, A y B con medias de\(\overline{X}_A\) y\(\overline{X}_B\), y desviaciones estándar de s A y s B. Los intervalos de confianza para\(\mu_A\) y para\(\mu_B\) son
\[\mu_A = \overline{X}_A \pm \frac {t s_A} {\sqrt{n_A}} \label{4.4}\]
\[\mu_B = \overline{X}_B \pm \frac {t s_B} {\sqrt{n_B}} \label{4.5}\]
donde n A y n B son los tamaños de muestra para A y para B. Nuestra hipótesis nula,\(H_0 \text{: } \mu_A = \mu_B\), es esa y cualquier diferencia entre\(\mu_A\) y\(\mu_B\) es el resultado de errores indeterminados que afectan los análisis. La hipótesis alternativa,\(H_A \text{: } \mu_A \neq \mu_B\), es que la diferencia entre\(\mu_A\) y\(\mu_B\) es demasiado grande para ser explicada por error indeterminado.
Para derivar una ecuación para t exp, asumimos que\(\mu_A\) es igual\(\mu_B\), y combinamos la ecuación\ ref {4.4} y la ecuación\ ref {4.5}
\[\overline{X}_A \pm \frac {t_\text{exp} s_A} {\sqrt{n_A}} = \overline{X}_B \pm \frac {t_\text{exp} s_B} {\sqrt{n_B}} \nonumber\]
Resolviendo\(|\overline{X}_A - \overline{X}_B|\) y usando una propagación de la incertidumbre, da
Por último, resolvemos para t exp
y compararlo con un valor crítico,\(t(\alpha, \nu)\), donde\(\alpha\) está la probabilidad de un error tipo 1, y\(\nu\) es los grados de libertad.
El problema 9 te pide usar una propagación de incertidumbre para mostrar que la Ecuación\ ref {4.6} es correcta.
Hasta el momento nuestro desarrollo de esta prueba t es similar al de comparar\(\overline{X}\) con\(\mu\), y sin embargo no tenemos suficiente información para evaluar la prueba t. ¿Ves el problema? Con dos conjuntos de datos independientes no está claro cuántos grados de libertad tenemos.
Supongamos que las varianzas\(s_A^2\) y\(s_B^2\) proporcionan estimaciones de las mismas\(\sigma^2\). En este caso podemos sustituir\(s_A^2\) y\(s_B^2\) con una varianza agrupada,\(s_\text{pool}^2\), esa es una mejor estimación para la varianza. Así, la Ecuación\ ref {4.7} se convierte
donde s pool, la desviación estándar agrupada, es
\[s_\text{pool} = \sqrt{\frac {(n_A - 1) s_A^2 + (n_B - 1)s_B^2} {n_A + n_B - 2}} \label{4.9}\]
El denominador de la Ecuación\ ref {4.9} nos muestra que los grados de libertad para una desviación estándar agrupada son\(n_A + n_B - 2\), que también son los grados de libertad para la prueba t. Tenga en cuenta que perdemos dos grados de libertad porque los cálculos para\(s_A^2\) y\(s_B^2\) requieren el cálculo previo de\(\overline{X}_A\) amd\(\overline{X}_B\).
Entonces, ¿cómo se determina si está bien juntar las varianzas? Use una prueba F.
Si\(s_A^2\) y\(s_B^2\) son significativamente diferentes, entonces calculamos t exp usando la Ecuación\ ref {4.7}. En este caso, encontramos los grados de libertad utilizando la siguiente ecuación imponente.
Debido a que los grados de libertad deben ser un entero, redondeamos al entero más cercano el valor\(\nu\) obtenido usando la ecuación\ ref {4.10}.
Ecuación\ ref {4.10}, que es de Miller, J.C.; Miller, J.N. Statistics for Analytical Chemistry, 2nd Ed., Ellis-Horward: Chichester, Reino Unido, 1988. En la 6ª Edición, los autores señalan que se han sugerido varias ecuaciones diferentes para el número de grados de libertad para t cuando s A y s B difieren, reflejando el hecho de que la determinación de grados de libertad es una aproximación. Una ecuación alternativa, que es utilizada por paquetes de software estadístico, como R, Minitab, Excel, es
\[\nu = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {\left( \frac {s_A^2} {n_A} \right)^2} {n_A - 1} + \frac {\left( \frac {s_B^2} {n_B} \right)^2} {n_B - 1}} = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {s_A^4} {n_A^2(n_A - 1)} + \frac {s_B^4} {n_B^2(n_B - 1)}} \nonumber\]
Para problemas típicos de la química analítica, los grados de libertad calculados son razonablemente insensibles a la elección de la ecuación.
Independientemente de si calculamos t exp usando la Ecuación\ ref {4.7} o la Ecuación\ ref {4.8}, rechazamos la hipótesis nula si t exp es mayor que\(t(\alpha, \nu)\) y conservamos la hipótesis nula si t exp es menor o igual a\(t(\alpha, \nu)\).
El Cuadro 4.4.1 proporciona los resultados de dos experimentos para determinar la masa de un centavo circulante de Estados Unidos. Determinar si existe una diferencia en las medias de estos análisis en\(\alpha = 0.05\).
Solución
Primero usamos una prueba F para determinar si podemos agrupar las varianzas. Completamos este análisis en el Ejemplo 4.6.3 , sin encontrar evidencia de una diferencia significativa, lo que significa que podemos juntar las desviaciones estándar, obteniendo
\[s_\text{pool} = \sqrt{\frac {(7 - 1)(0.051)^2 + (5 - 1)(0.037)^2} {7 + 5 - 2}} = 0.0459 \nonumber\]
con 10 grados de libertad. Para comparar las medias utilizamos las siguientes hipótesis nulas e hipótesis alternativas
\[H_0 \text{: } \mu_A = \mu_B \quad \quad \quad H_A \text{: } \mu_A \neq \mu_B \nonumber\]
Debido a que estamos usando la desviación estándar agrupada, calculamos t exp usando la ecuación\ ref {4.8}.
\[t_\text{exp} = \frac {|3.117 - 3.081|} {0.0459} \times \sqrt{\frac {7 \times 5} {7 + 5}} = 1.34 \nonumber\]
El valor crítico para t (0.05, 10), del Apéndice 4, es 2.23. Debido a que t exp es menor que t (0.05, 10) conservamos la hipótesis nula. Porque no\(\alpha = 0.05\) tenemos evidencia de que los dos juegos de centavos sean significativamente diferentes.
Un método para determinar el% w/w de Na 2 CO 3 en la ceniza de sosa es usar una titulación ácido-base. Cuando dos analistas analizan la misma muestra de carbonato de sodio obtienen los resultados que aquí se muestran.
Analista A:\(86.82 \% \quad 87.04 \% \quad 86.93 \% \quad 87.01 \% \quad 86.20 \% \quad 87.00 \%\)
Analista B:\(81.01 \% \quad 86.15 \% \quad 81.73 \% \quad 83.19 \% \quad 80.27 \% \quad 83.93 \% \quad\)
Determinar si la diferencia en los valores medios es significativa en\(\alpha = 0.05\).
Solución
Comenzamos reportando la media y desviación estándar para cada analista.
\[\overline{X}_A = 86.83\% \quad \quad s_A = 0.32\% \nonumber\]
\[\overline{X}_B = 82.71\% \quad \quad s_B = 2.16\% \nonumber\]
Para determinar si podemos usar una desviación estándar agrupada, primero completamos una prueba F usando las siguientes hipótesis nulas y alternativas.
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_A \text{: } s_A^2 \neq s_B^2 \nonumber\]
Calculando F exp, obtenemos un valor de
\[F_\text{exp} = \frac {(2.16)^2} {(0.32)^2} = 45.6 \nonumber\]
Debido a que F exp es mayor que el valor crítico de 7.15 para F (0.05, 5, 5) del Apéndice 5, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que existe una diferencia significativa entre las varianzas; así, no podemos calcular un conjunto desviación estándar.
Para comparar las medias de los dos analistas utilizamos las siguientes hipótesis nulas y alternativas.
\[H_0 \text{: } \overline{X}_A = \overline{X}_B \quad \quad \quad H_A \text{: } \overline{X}_A \neq \overline{X}_B \nonumber\]
Debido a que no podemos juntar las desviaciones estándar, calculamos t exp usando la ecuación\ ref {4.7} en lugar de la ecuación\ ref {4.8}
\[t_\text{exp} = \frac {|86.83 - 82.71|} {\sqrt{\frac {(0.32)^2} {6} + \frac {(2.16)^2} {6}}} = 4.62 \nonumber\]
y calcular los grados de libertad usando la Ecuación\ ref {4.10}.
\[\nu = \frac {\left( \frac {(0.32)^2} {6} + \frac {(2.16)^2} {6} \right)^2} {\frac {\left( \frac {(0.32)^2} {6} \right)^2} {6 + 1} + \frac {\left( \frac {(2.16)^2} {6} \right)^2} {6 + 1}} - 2 = 5.3 \approx 5 \nonumber\]
Del Apéndice 4, el valor crítico para t (0.05, 5) es 2.57. Debido a que t exp es mayor que t (0.05, 5) rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que las medias para los dos analistas son significativamente diferentes en\(\alpha = 0.05\).
Para comparar dos lotes de producción de tabletas de aspirina, se recolectan muestras de cada una y las analizan, obteniendo los siguientes resultados (en mg de aspirina/tableta).
Lote 1:\(256 \quad 248 \quad 245 \quad 245 \quad 244 \quad 248 \quad 261\)
Lote 2:\(241 \quad 258 \quad 241 \quad 244 \quad 256 \quad 254\)
¿Hay alguna evidencia de\(\alpha = 0.05\) que existe una diferencia significativa en la varianza entre los resultados de estas dos muestras? Estos son los mismos datos del Ejercicio 4.6.2 .
- Responder
-
Para comparar las medias de los dos lotes, utilizamos una prueba t desapareada de la hipótesis nula\(H_0 \text{: } \overline{X}_\text{Lot 1} = \overline{X}_\text{Lot 2}\) y la hipótesis alternativa\(H_A \text{: } \overline{X}_\text{Lot 1} \neq \overline{X}_\text{Lot 2}\). Debido a que no hay evidencia que sugiera una diferencia en las varianzas (ver Ejercicio 4.6.2 ) agrupamos las desviaciones estándar, obteniendo un s pool de
\[s_\text{pool} = \sqrt{\frac {(7 - 1) (6.451)^2 + (6 - 1) (7.849)^2} {7 + 6 - 2}} = 7.121 \nonumber\]
Las medias para las dos muestras son 249.57 mg para el Lote 1 y 249.00 mg para el Lote 2. El valor para t exp es
\[t_\text{exp} = \frac {|249.57 - 249.00|} {7.121} \times \sqrt{\frac {7 \times 6} {7 + 6}} = 0.1439 \nonumber\]
El valor crítico para t (0.05, 11) es 2.204. Debido a que t exp es menor que t (0.05, 11), conservamos la hipótesis nula y no encontramos evidencia de\(\alpha = 0.05\) que exista una diferencia significativa entre las medias para los dos lotes de tabletas de aspirina.
Datos emparejados
Supongamos que estamos evaluando un nuevo método para monitorear las concentraciones de glucosa en sangre en pacientes. Una parte importante de la evaluación de un nuevo método es compararlo con un método establecido. ¿Cuál es la mejor manera de recopilar datos para este estudio? Debido a que la variación en los niveles de glucosa en sangre entre los pacientes es grande, es posible que no podamos detectar una diferencia pequeña pero significativa entre los métodos si utilizamos diferentes pacientes para recopilar datos para cada método. El uso de datos pareados, en los que analizamos la sangre de cada paciente utilizando ambos métodos, evita que una gran varianza dentro de una población afecte negativamente a una prueba t de medias.
Los niveles típicos de glucosa en sangre para la mayoría de los individuos no diabéticos oscilan entre 80—120 mg/dL (4.4—6.7 mM), elevándose a 140 mg/dL (7.8 mM) poco después de comer. Los niveles más altos son comunes en individuos que son prediabéticos o diabéticos.
Cuando usamos datos emparejados primero calculamos la diferencia, d i, entre los valores emparejados para cada muestra. Usando estos valores de diferencia, calculamos entonces la diferencia promedio,\(\overline{d}\), y la desviación estándar de las diferencias, s d. La hipótesis nula,\(H_0 \text{: } d = 0\), es que no hay diferencia entre las dos muestras, y la hipótesis alternativa,\(H_A \text{: } d \neq 0\), es que la diferencia entre las dos muestras es significativa.
El estadístico de prueba, t exp, se deriva de un intervalo de confianza alrededor\(\overline{d}\)
\[t_\text{exp} = \frac {|\overline{d}| \sqrt{n}} {s_d} \nonumber\]
donde n es el número de muestras emparejadas. Como es cierto para otras formas de la prueba t, comparamos t exp con\(t(\alpha, \nu)\), donde los grados de libertad,\(\nu\), es n — 1. Si t exp es mayor que\(t(\alpha, \nu)\), entonces rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Conservamos la hipótesis nula si t exp es menor o igual a t (a, o). Esto se conoce como prueba t pareada.
Marecek et. al. desarrollaron un nuevo método electroquímico para la determinación rápida de la concentración del antibiótico monensina en cubas de fermentación [Marecek, V.; Janchenova, H.; Brezina, M.; Betti, M. Anal. Chim. Acta 1991, 244, 15—19]. El método estándar para el análisis es una prueba de actividad microbiológica, que es difícil de completar y requiere mucho tiempo. Se recolectaron muestras de las cubas de fermentación en diversos momentos durante la producción y se analizó la concentración de monensina mediante ambos métodos. Los resultados, en partes por mil (ppt), se reportan en la siguiente tabla.
| Muestra | Microbiológicos | Electroquímica |
|---|---|---|
| 1 | 129.5 | 132.3 |
| 2 | 89.6 | 91.0 |
| 3 | 76.6 | 73.6 |
| 4 | 52.2 | 58.2 |
| 5 | 110.8 | 104.2 |
| 6 | 50.4 | 49.9 |
| 7 | 72.4 | 82.1 |
| 8 | 141.4 | 154.1 |
| 9 | 75.0 | 73.4 |
| 10 | 34.1 | 38.1 |
| 11 | 60.3 | 60.1 |
¿Hay una diferencia significativa entre los métodos en\(\alpha = 0.05\)?
Solución
La adquisición de muestras durante un período prolongado de tiempo introduce un cambio sustancial dependiente del tiempo en la concentración de monensina. Debido a que la variación en la concentración entre muestras es tan grande, utilizamos una prueba t pareada con las siguientes hipótesis nulas y alternativas.
\[H_0 \text{: } \overline{d} = 0 \quad \quad \quad H_A \text{: } \overline{d} \neq 0 \nonumber\]
Definir la diferencia entre los métodos como
\[d_i = (X_\text{elect})_i - (X_\text{micro})_i \nonumber\]
calculamos la diferencia para cada muestra.
| muestra | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| \(d_i\) | 2.8 | 1.4 | —3.0 | 6.0 | —6.6 | —0.5 | 9.7 | 12.7 | —1.6 | 4.0 | —0.2 |
La media y la desviación estándar para las diferencias son, respectivamente, 2.25 ppt y 5.63 ppt. El valor de t exp es
\[t_\text{exp} = \frac {|2.25| \sqrt{11}} {5.63} = 1.33 \nonumber\]
que es menor que el valor crítico de 2.23 para t (0.05, 10) del Apéndice 4. Conservamos la hipótesis nula y no encontramos evidencia de una diferencia significativa en los métodos en\(\alpha = 0.05\).
Supongamos que está estudiando la distribución del zinc en un lago y quiere saber si existe una diferencia significativa entre la concentración de Zn 2 + en la interfaz sedimento-agua y su concentración en la interfaz aire-agua. Se recolectan muestras de seis ubicaciones, cerca del centro del lago, cerca de su salida de drenaje, etc., obteniendo los resultados (en mg/L) que se muestran en la tabla. Usando estos datos, determinar si existe una diferencia significativa entre la concentración de Zn 2 + en las dos interfaces en\(\alpha = 0.05\). Completar este análisis tratando los datos como (a) desapareados y como (b) emparejados. Comenta brevemente tus resultados.
| Ubicación | Interfaz aire-agua | Interfaz Sedimento-Agua |
| 1 | 0.430 | 0.415 |
| 2 | 0.266 | 0.238 |
| 3 | 0.457 | 0.390 |
| 4 | 0.531 | 0.410 |
| 5 | 0.707 | 0.605 |
| 6 | 0.716 | 0.609 |
Completar este análisis tratando los datos como (a) desapareados y como (b) emparejados. Comenta brevemente tus resultados.
- Responder
-
Tratar como Datos No Pareados: La media y la desviación estándar para la concentración de Zn 2 + en la interfaz aire-agua son 0.5178 mg/L y 0.1732 mg/L, respectivamente, y los valores para la interfaz sedimento-agua son 0.4445 mg/L y 0.1418 mg/L, respectivamente. Una prueba F de las varianzas da una F exp de 1.493 y una F (0.05, 5, 5) de 7.146. Debido a que F exp es menor que F (0.05, 5, 5), no tenemos evidencia de que la diferencia en varianzas sea significativa.\(\alpha = 0.05\) La combinación de las desviaciones estándar da un pool s de 0.1582 mg/L y una prueba t desapareada da t exp como 0.8025. Debido a que t exp es menor que t (0.05, 11), que es 2.204, no tenemos evidencia de que exista una diferencia en la concentración de Zn 2 + entre las dos interfaces.
Tratar como Datos Pareados: Para tratar como datos pareados necesitamos calcular la diferencia, d i, entre la concentración de Zn 2 + en la interfaz aire-agua y en la interfaz sedimento-agua para cada ubicación, donde
\[d_i = \left( \text{[Zn}^{2+} \text{]}_\text{air-water} \right)_i - \left( \text{[Zn}^{2+} \text{]}_\text{sed-water} \right)_i \nonumber\]
La diferencia media es de 0.07333 mg/L con una desviación estándar de 0.0441 mg/L; la hipótesis nula y la hipótesis alternativa son
\[H_0 \text{: } \overline{d} = 0 \quad \quad \quad H_A \text{: } \overline{d} \neq 0 \nonumber\]
y el valor de t exp es
\[t_\text{exp} = \frac {|0.07333| \sqrt{6}} {0.0441} = 4.073 \nonumber\]
Debido a que t exp es mayor que t (0.05, 5), que es 2.571, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que existe una diferencia significativa en la concentración de Zn 2 + entre la interfaz aire-agua y el sedimento- interfaz de agua.
La diferencia en la concentración de Zn 2 + entre ubicaciones es mucho mayor que la diferencia en la concentración de Zn 2 + entre las interfaces. Debido a que el interés está en estudiar la diferencia entre las interfaces, la mayor desviación estándar al tratar los datos como desapareados aumenta la probabilidad de retener incorrectamente la hipótesis nula, un error tipo 2.
Un requisito importante para una prueba t pareada es que los errores determinados e indeterminados que afectan el análisis deben ser independientes de la concentración del analito. Si este no es el caso, entonces una muestra con una concentración inusualmente alta de analito tendrá un d i inusualmente grande. Incluir esta muestra en el cálculo de\(\overline{d}\) y s d da una estimación sesgada para la media esperada y la desviación estándar. Esto rara vez es un problema para muestras que abarcan un rango limitado de concentraciones de analitos, como las del Ejemplo 4.6.6 o Ejercicio 4.6.4 . Sin embargo, cuando los datos emparejados abarcan un amplio rango de concentraciones, la magnitud de las fuentes de error determinadas e indeterminadas puede no ser independiente de la concentración del analito; cuando es verdad, una prueba t pareada puede dar resultados engañosos porque los datos emparejados con el mayor absoluto los errores determinados e indeterminados dominarán\(\overline{d}\). En esta situación un análisis de regresión, que es el tema del siguiente capítulo, es el método más apropiado para comparar los datos.
Valores atípicos
Anteriormente en el capítulo examinamos varios conjuntos de datos consistentes en la masa de un centavo circulante de Estados Unidos. Table 4.6.1 proporciona un conjunto de datos más. ¿Se nota algo inusual en estos datos? De los 112 centavos incluidos en la Tabla 4.4.1 y en la Tabla 4.4.3, ningún centavo pesaba menos de 3 g. En la Tabla 4.6.1, sin embargo, la masa de un centavo es inferior a 3 g. Podríamos preguntarnos si la masa de este centavo es tan diferente de las otras centavos que está en error.
| 3.067 | 2.514 | 3.094 |
| 3.049 | 3.048 | 3.109 |
| 3.039 | 3.079 | 3.102 |
Una medición que no es consistente con otras mediciones se denomina valor atípico. Un valor atípico puede existir por muchas razones: el valor atípico podría pertenecer a una población diferente (¿es esto un centavo canadiense?) ; el valor atípico podría ser una muestra contaminada o alterada de otra manera (¿El centavo está dañado o inusualmente sucio?) ; o el valor atípico puede resultar de un error en el análisis (¿Olvidamos tara la balanza?). Independientemente de su fuente, la presencia de un valor atípico compromete cualquier análisis significativo de nuestros datos. Hay muchas pruebas de significación que podemos usar para identificar un posible valor atípico, tres de las cuales presentamos aquí.
Prueba Q de Dixon
Una de las pruebas de significancia más comunes para identificar un valor atípico es la prueba Q de Dixon. La hipótesis nula es que no hay valores atípicos, y la hipótesis alternativa es que hay un valor atípico. La prueba Q compara la brecha entre el valor atípico sospechoso y su vecino numérico más cercano con el rango de todo el conjunto de datos (Figura 4.6.2 ).
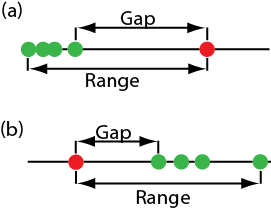
El estadístico de prueba, Q exp, es
\[Q_\text{exp} = \frac {\text{gap}} {\text{range}} = \frac {|\text{outlier's value} - \text{nearest value}|} {\text{largest value} - \text{smallest value}} \nonumber\]
Esta ecuación es apropiada para evaluar un único valor atípico. Otras formas de la prueba Q de Dixon permiten su extensión a la detección de múltiples valores atípicos [Rorabacher, D. B. Anal. Chem. 1991, 63, 139—146].
El valor de Q exp se compara con un valor crítico,\(Q(\alpha, n)\), donde\(\alpha\) está la probabilidad de que rechacemos un punto de datos válido (un error tipo 1) y n es el número total de puntos de datos. Para proteger contra el rechazo de un punto de datos válido, generalmente aplicamos la prueba Q de dos colas más conservadora, aunque el valor atípico posible es el valor más pequeño o el mayor en el conjunto de datos. Si Q exp es mayor que\(Q(\alpha, n)\), entonces rechazamos la hipótesis nula y podemos excluir el valor atípico. Conservamos el posible valor atípico cuando Q exp es menor o igual a\(Q(\alpha, n)\). La Tabla 4.6.2 proporciona valores\(Q(\alpha, n)\) para un conjunto de datos que tiene 3—10 valores. Una tabla más extensa se encuentra en el Apéndice 6. Valores para\(Q(\alpha, n)\) asumir una distribución normal subyacente.
| n | Q (0.05, n) |
|---|---|
| 3 | 0.970 |
| 4 | 0.829 |
| 5 | 0.710 |
| 6 | 0.625 |
| 7 | 0.568 |
| 8 | 0.526 |
| 9 | 0.493 |
| 10 | 0.466 |
Prueba de Grubb
Si bien la prueba Q de Dixon es un método común para evaluar valores atípicos, ya no es favorecida por la Organización Internacional de Normalización (ISO), que recomienda la prueba de Grubb. Existen varias versiones de la prueba de Grubb dependiendo del número de posibles valores atípicos. Aquí consideraremos el caso donde hay un solo presunto valor atípico.
Para obtener detalles sobre esta recomendación, consulte la Guía ISO de Normas Internacionales 5752-2 “Exactitud (veracidad y precisión) de los métodos y resultados de medición—Parte 2: métodos básicos para la determinación de la repetibilidad y reproducibilidad de un método de medición estándar”, 1994.
El estadístico de prueba para la prueba de Grubb, G exp, es la distancia entre la media de la muestra\(\overline{X}\), y el valor atípico potencial\(X_\text{out}\), en términos de la desviación estándar de la muestra, s.
\[G_\text{exp} = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber\]
Comparamos el valor de G exp con un valor crítico\(G(\alpha, n)\), donde\(\alpha\) está la probabilidad de que rechacemos un punto de datos válido y n es el número de puntos de datos en la muestra. Si G exp es mayor que\(G(\alpha, n)\), entonces podemos rechazar el punto de datos como un valor atípico, de lo contrario conservamos el punto de datos como parte de la muestra. La Tabla 4.6.3 proporciona valores para G (0.05, n) para una muestra que contiene 3—10 valores. Una tabla más extensa se encuentra en el Apéndice 7. Valores para\(G(\alpha, n)\) asumir una distribución normal subyacente.
| n | G (0.05, n) |
|---|---|
| 3 | 1.115 |
| 4 | 1.481 |
| 5 | 1.715 |
| 6 | 1.887 |
| 7 | 2.020 |
| 8 | 2.126 |
| 9 | 2.215 |
| 10 | 2.290 |
Criterio de Chauvenet
Nuestro método final para identificar un valor atípico es el criterio de Chauvenet. A diferencia de la prueba Q de Dixon y la prueba de Grubb, puedes aplicar este método a cualquier distribución siempre que sepas cómo calcular la probabilidad de un resultado en particular. El criterio de Chauvenet establece que podemos rechazar un punto de datos si la probabilidad de obtener el valor del punto de datos es menor que (2 n) —1, donde n es el tamaño de la muestra. Por ejemplo, si n = 10, un resultado con una probabilidad menor que\((2 \times 10)^{-1}\), o 0.05, se considera un valor atípico.
Para calcular la probabilidad de un valor atípico potencial, primero calculamos su desviación estandarizada, z
\[z = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber\]
donde\(X_\text{out}\) es el valor atípico potencial,\(\overline{X}\) es la media de la muestra y s es la desviación estándar de la muestra. Tenga en cuenta que esta ecuación es idéntica a la ecuación para G exp en la prueba de Grubb. Para una distribución normal, podemos encontrar la probabilidad de obtener un valor de z usando la tabla de probabilidad en el Apéndice 3.
El cuadro 4.6.1 contiene las masas por nueve centavos circulantes de Estados Unidos. Una entrada, 2.514 g, parece ser un valor atípico. Determine si este centavo es un valor atípico usando una prueba Q, una prueba de Grubb y el criterio de Chauvenet. Para la prueba Q y la prueba de Grubb, vamos\(\alpha = 0.05\).
Solución
Para la prueba Q, el valor para Q exp es
\[Q_\text{exp} = \frac {|2.514 - 3.039|} {3.109 - 2.514} = 0.882 \nonumber\]
De la Tabla 4.6.2 , el valor crítico para Q (0.05, 9) es 0.493. Debido a que Q exp es mayor que Q (0.05, 9), podemos suponer que el centavo con una masa de 2.514 g probablemente sea un valor atípico.
Para la prueba de Grubb primero necesitamos la media y la desviación estándar, que son 3.011 g y 0.188 g, respectivamente. El valor para G exp es
\[G_\text{exp} = \frac {|2.514 - 3.011} {0.188} = 2.64 \nonumber\]
Usando Table 4.6.3 , encontramos que el valor crítico para G (0.05, 9) es 2.215. Debido a que G exp es mayor que G (0.05, 9), podemos suponer que el centavo con una masa de 2.514 g probablemente es un valor atípico.
Para el criterio de Chauvenet, la probabilidad crítica es\((2 \times 9)^{-1}\), o 0.0556. El valor de z es el mismo que G exp, o 2.64. Usando el Apéndice 3, la probabilidad para z = 2.64 es 0.00415. Debido a que la probabilidad de obtener una masa de 0.2514 g es menor que la probabilidad crítica, podemos suponer que el centavo con una masa de 2.514 g probable es un valor atípico.
Debe tener precaución al usar una prueba de significancia para valores atípicos porque existe la posibilidad de que rechace un resultado válido. Además, debes evitar rechazar un valor atípico si lleva a una precisión mucho mejor de lo esperado en base a una propagación de la incertidumbre. Ante estas preocupaciones no es sorprendente que algunos estadísticos adviertan contra la eliminación de valores atípicos [Deming, W. E. Statistical Analysis of Data; Wiley: New York, 1943 (reeditado por Dover: New York, 1961); p. 171].
También puede adoptar un requisito más estricto para rechazar datos. Al usar la prueba de Grubb, por ejemplo, las directrices ISO 5752 sugieren retener un valor si la probabilidad de rechazarlo es mayor que\(\alpha = 0.05\), y marcar un valor como “rezagado” si la probabilidad de rechazarlo es entre\(\alpha = 0.05\) y\(\alpha = 0.01\). Un “rezagado” se retiene a menos que haya razones imperiosas para su rechazo. Los lineamientos recomiendan utilizar\(\alpha = 0.01\) como criterio mínimo para rechazar un posible valor atípico.
Por otro lado, las pruebas para detectar valores atípicos pueden proporcionar información útil si tratamos de entender la fuente del presunto valor atípico. Por ejemplo, el valor atípico en la Tabla 4.6.1 representa un cambio significativo en la masa de un centavo (una disminución de aproximadamente 17% en la masa), que es el resultado de un cambio en la composición del centavo estadounidense. En 1982 la composición de un centavo estadounidense cambió de una aleación de latón que era 95% w/w Cu y 5% w/w Zn (con una masa nominal de 3.1 g), a un núcleo de zinc puro cubierto con cobre (con una masa nominal de 2.5 g) [Richardson, T. H. J. Chem. Educ. 1991, 68, 310—311]. Los centavos en la Tabla 4.6.1 , por lo tanto, se extrajeron de diferentes poblaciones.


