5.4: Regresión lineal y curvas de calibración
- Page ID
- 75830
En una estandarización externa de un solo punto determinamos el valor de k A midiendo la señal para un único estándar que contiene una concentración conocida de analito. Usando este valor de k A y la señal de nuestra muestra, calculamos entonces la concentración de analito en nuestra muestra (ver Ejemplo 5.3.1). Con una sola determinación de k A, un análisis cuantitativo utilizando una estandarización externa de un solo punto es sencillo.
Una estandarización de múltiples puntos presenta un problema más difícil. Considere los datos en la Tabla 5.4.1 para una estandarización externa de múltiples puntos. ¿Cuál es nuestra mejor estimación de la relación entre S std y C std? Es tentador tratar estos datos como cinco estandarizaciones separadas de un solo punto, determinando k A para cada estándar y reportando el valor medio para los cinco ensayos. A pesar de su simplicidad, esta no es una forma apropiada de tratar una estandarización de múltiples puntos.
| \(C_{std}\)(unidades arbitrarias) | \(S_{std}\)(unidades arbitrarias) | \(k_A = S_{std}/C_{std}\) |
|---|---|---|
| \ (C_ {std}\) (unidades arbitrarias) ">0.000 | \ (S_ {std}\) (unidades arbitrarias) ">0.00 | \ (K_a = S_ {std} /C_ {std}\) ">— |
| \ (C_ {std}\) (unidades arbitrarias) ">0.100 | \ (S_ {std}\) (unidades arbitrarias) ">12.36 | \ (K_a = S_ {std} /C_ {std}\) ">123.6 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.200 | \ (S_ {std}\) (unidades arbitrarias) ">24.83 | \ (K_a = S_ {std} /C_ {std}\) ">124.2 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.300 | \ (S_ {std}\) (unidades arbitrarias) ">35.91 | \ (K_a = S_ {std} /C_ {std}\) ">119.7 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.400 | \ (S_ {std}\) (unidades arbitrarias) ">48.79 | \ (K_a = S_ {std} /C_ {std}\) ">122.0 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.500 | \ (S_ {std}\) (unidades arbitrarias) ">60.42 | \ (K_a = S_ {std} /C_ {std}\) ">122.8 |
| \ (C_ {std}\) (unidades arbitrarias)” class="lt-chem-132505"> | \ (S_ {std}\) (unidades arbitrarias) "> | \ (K_a = S_ {std} /C_ {std}\) ">media k A = 122.5 |
Entonces, ¿por qué es inapropiado calcular un valor promedio para k A usando los datos de la Tabla 5.4.1 ? En una estandarización de punto único asumimos que el reactivo en blanco (la primera fila de la Tabla 5.4.1 ) corrige todas las fuentes constantes de error determinado. Si este no es el caso, entonces el valor de k A de una estandarización de un solo punto tiene un error constante determinado. La Tabla 5.4.2 demuestra cómo un error constante no corregido afecta nuestra determinación de k A. Las tres primeras columnas muestran la concentración de analito en un conjunto de estándares, C std, la señal sin ninguna fuente de error constante, S std, y el valor real de k A para cinco normas. Como esperamos, el valor de k A es el mismo para cada estándar. En la cuarta columna agregamos un error constante determinado de +0.50 a las señales, (S std) e. La última columna contiene los valores aparentes correspondientes de k A. Tenga en cuenta que obtenemos un valor diferente de k A para cada estándar y que cada k A aparente es mayor que el valor verdadero.
| \(C_{std}\) |
\(S_{std}\) |
\(k_A = S_{std}/C_{std}\) |
\((S_{std})_e\) |
\(k_A = (S_{std})_e/C_{std}\) |
|---|---|---|---|---|
| \ (C_ {std}\) ">1.00 | \ (S_ {std}\) (sin error constante) ">1.00 | \ (K_a = S_ {std} /C_ {std}\) (real) ">1.00 | \ ((S_ {std}) _e\) (con error constante) ">1.50 | \ (K_a = (S_ {std}) _e/C_ {std}\) (aparente) ">1.50 |
| \ (C_ {std}\) ">2.00 | \ (S_ {std}\) (sin error constante) ">2.00 | \ (K_a = S_ {std} /C_ {std}\) (real) ">1.00 | \ ((S_ {std}) _e\) (con error constante) ">2.50 | \ (K_a = (S_ {std}) _e/C_ {std}\) (aparente) ">1.25 |
| \ (C_ {std}\) ">3.00 | \ (S_ {std}\) (sin error constante) ">3.00 | \ (K_a = S_ {std} /C_ {std}\) (real) ">1.00 | \ ((S_ {std}) _e\) (con error constante) ">3.50 | \ (K_a = (S_ {std}) _e/C_ {std}\) (aparente) ">1.17 |
| \ (C_ {std}\) ">4.00 | \ (S_ {std}\) (sin error constante) ">4.00 | \ (K_a = S_ {std} /C_ {std}\) (real) ">1.00 | \ ((S_ {std}) _e\) (con error constante) ">4.50 | \ (K_a = (S_ {std}) _e/C_ {std}\) (aparente) ">1.13 |
| \ (C_ {std}\) ">5.00 | \ (S_ {std}\) (sin error constante) ">5.00 | \ (K_a = S_ {std} /C_ {std}\) (real) ">1.00 | \ ((S_ {std}) _e\) (con error constante) ">5.50 | \ (K_a = (S_ {std}) _e/C_ {std}\) (aparente) ">1.10 |
| \ (C_ {std}\)” class="lt-chem-132505"> | \ (S_ {std}\) (sin error constante) "> | \ (K_a = S_ {std} /C_ {std}\) (real) ">media k A (verdadero) = 1.00 | \ ((S_ {std}) _e\) (con error constante) "> | \ (K_a = (S_ {std}) _e/C_ {std}\) (aparente) ">media k A (aparente) = 1.23 |
¿Cómo encontramos la mejor estimación para la relación entre la señal y la concentración de analito en una estandarización de múltiples puntos? La Figura 5.4.1 muestra los datos en la Tabla 5.4.1 trazados como una curva de calibración normal. Aunque los datos ciertamente parecen caer a lo largo de una línea recta, la curva de calibración real no es intuitivamente obvia. El proceso de determinación de la mejor ecuación para la curva de calibración se denomina regresión lineal.
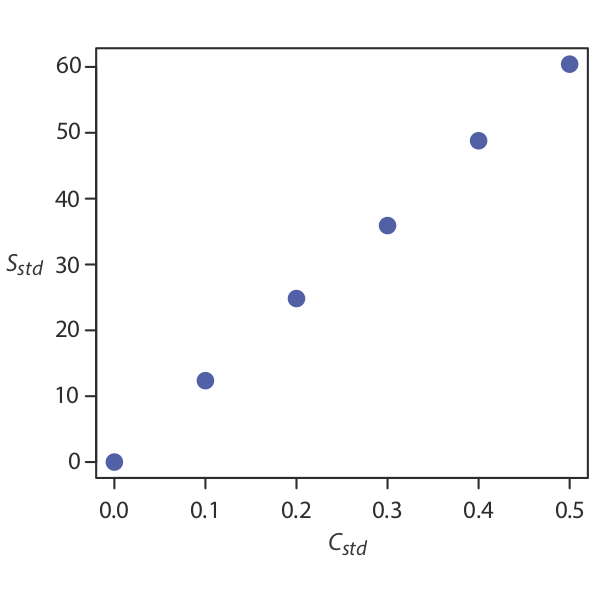
Regresión lineal de curvas de calibración de línea recta
Cuando una curva de calibración es una línea recta, la representamos usando la siguiente ecuación matemática
\[y = \beta_0 + \beta_1 x \label{5.1}\]
donde y es la señal del analito, S std, y x es la concentración del analito, C std. Las constantes\(\beta_0\) y\(\beta_1\) son, respectivamente, la intersección y esperada de la curva de calibración y su pendiente esperada. Debido a la incertidumbre en nuestras mediciones, lo mejor que podemos hacer es estimar valores para\(\beta_0\) y\(\beta_1\), que representamos como b 0 y b 1. El objetivo de un análisis de regresión lineal es determinar las mejores estimaciones para b 0 y b 1. La forma en que hagamos esto depende de la incertidumbre en nuestras mediciones.
Regresión lineal no ponderada con errores en y
El método más común para completar la regresión lineal para la Ecuación\ ref {5.1} hace tres suposiciones:
- que la diferencia entre nuestros datos experimentales y la línea de regresión calculada es el resultado de errores indeterminados que afectan a y
- que los errores indeterminados que afectan a y se distribuyen normalmente
- que los errores indeterminados en y son independientes del valor de x
Debido a que asumimos que los errores indeterminados son los mismos para todos los estándares, cada estándar contribuye por igual en nuestra estimación de la pendiente y la intersección y. Por esta razón el resultado se considera una regresión lineal no ponderada.
El segundo supuesto generalmente es cierto debido al teorema del límite central, que consideramos en el Capítulo 4. La validez de los dos supuestos restantes es menos obvia y debes evaluarlos antes de aceptar los resultados de una regresión lineal. En particular la primera suposición siempre es sospechosa porque ciertamente hay algún error indeterminado en la medición de x. Sin embargo, cuando preparamos una curva de calibración, no es raro encontrar que la incertidumbre en la señal, S std, es significativamente mayor que la incertidumbre en la concentración del analito, C std. En tales circunstancias el primer supuesto suele ser razonable.
Cómo funciona una regresión lineal
Para entender la lógica de una regresión lineal consideremos el ejemplo mostrado en la Figura 5.4.2 , que muestra tres puntos de datos y dos posibles líneas rectas que podrían explicar razonablemente los datos. ¿Cómo decidimos qué tan bien estas líneas rectas se ajustan a los datos y cómo determinamos la mejor línea recta?
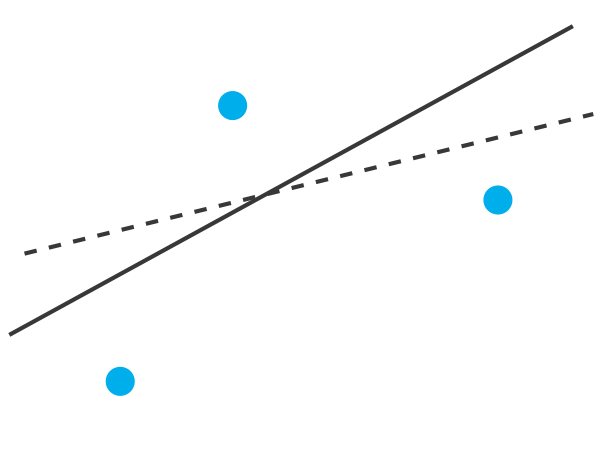
Centrémonos en la línea continua en la Figura 5.4.2 . La ecuación para esta línea es
\[\hat{y} = b_0 + b_1 x \label{5.2}\]
donde b 0 y b 1 son estimaciones para la intersección y y la pendiente, y\(\hat{y}\) es el valor predicho de y para cualquier valor de x. Porque suponemos que toda incertidumbre es el resultado de errores indeterminados en y, la diferencia entre y y\(\hat{y}\) para cada valor de x es el error residual, r, en nuestro modelo matemático.
\[r_i = (y_i - \hat{y}_i) \nonumber\]
La Figura 5.4.3 muestra los errores residuales para los tres puntos de datos. Cuanto menor sea el error residual total, R, que definimos como
\[R = \sum_{i = 1}^{n} (y_i - \hat{y}_i)^2 \label{5.3}\]
mejor es el ajuste entre la línea recta y los datos. En un análisis de regresión lineal, buscamos valores de b 0 y b 1 que den el menor error residual total.
La razón para cuadrar los errores residuales individuales es evitar que un error residual positivo cancele un error residual negativo. Esto lo has visto antes en las ecuaciones para la muestra y las desviaciones estándar de la población. También se puede ver a partir de esta ecuación por qué a una regresión lineal se le llama a veces el método de mínimos cuadrados.
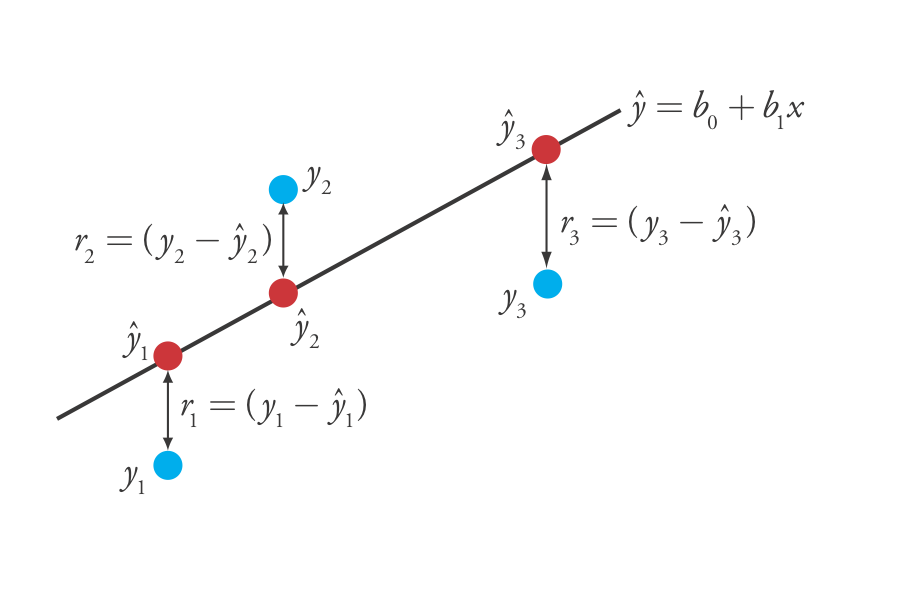
Encontrar el Desnivel y la Intercepción y
Aunque no desarrollaremos formalmente las ecuaciones matemáticas para un análisis de regresión lineal, se pueden encontrar las derivaciones en muchos textos estadísticos estándar [Véase, por ejemplo, Draper, N. R.; Smith, H. Applied Regression Analysis, 3a ed.; Wiley: New York, 1998]. La ecuación resultante para la pendiente, b 1, es
y la ecuación para la intersección y, b 0, es
\[b_0 = \frac {\sum_{i = 1}^{n} y_i - b_1 \sum_{i = 1}^{n} x_i} {n} \label{5.5}\]
Aunque la Ecuación\ ref {5.4} y la Ecuación\ ref {5.5} parecen formidables, solo es necesario evaluar las siguientes cuatro sumas
\[\sum_{i = 1}^{n} x_i \quad \sum_{i = 1}^{n} y_i \quad \sum_{i = 1}^{n} x_i y_i \quad \sum_{i = 1}^{n} x_i^2 \nonumber\]
Muchas calculadoras, hojas de cálculo y otros paquetes de software estadístico son capaces de realizar un análisis de regresión lineal basado en este modelo. Para ahorrar tiempo y evitar cálculos tediosos, aprenda a usar una de estas herramientas (y consulte la Sección 5.6 para obtener detalles sobre cómo completar un análisis de regresión lineal usando Excel y R.). Para fines ilustrativos se muestran en detalle los cálculos necesarios en el siguiente ejemplo.
La ecuación\ ref {5.4} y la ecuación\ ref {5.5} se escriben en términos de las variables generales x e y. Al trabajar a través de este ejemplo, recuerde que x corresponde a C std, y que y corresponde a S std.
Usando los datos de Table 5.4.1 , determinar la relación entre S std y C std usando una regresión lineal no ponderada.
Solución
Comenzamos configurando una tabla que nos ayude a organizar el cálculo.
| \(x_i\) | \(y_i\) | \(x_i y_i\) | \(x_i^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (x_i y_i\) ">0.000 | \ (x_i^2\) ">0.000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12.36 | \ (x_i y_i\) ">1.236 | \ (x_i^2\) ">0.010 |
| \ (x_i\) ">0.200 | \ (y_i\) ">24.83 | \ (x_i y_i\) ">4.966 | \ (x_i^2\) ">0.040 |
| \ (x_i\) ">0.300 | \ (y_i\) ">35.91 | \ (x_i y_i\) ">10.773 | \ (x_i^2\) ">0.090 |
| \ (x_i\) ">0.400 | \ (y_i\) ">48.79 | \ (x_i y_i\) ">19.516 | \ (x_i^2\) ">0.160 |
| \ (x_i\) ">0.500 | \ (y_i\) ">60.42 | \ (x_i y_i\) ">30.210 | \ (x_i^2\) ">0.250 |
Sumando los valores en cada columna da
\[\sum_{i = 1}^{n} x_i = 1.500 \quad \sum_{i = 1}^{n} y_i = 182.31 \quad \sum_{i = 1}^{n} x_i y_i = 66.701 \quad \sum_{i = 1}^{n} x_i^2 = 0.550 \nonumber\]
Sustituyendo estos valores en la Ecuación\ ref {5.4} y Ecuación\ ref {5.5}, encontramos que la pendiente y la intersección y son
\[b_1 = \frac {(6 \times 66.701) - (1.500 \times 182.31)} {(6 \times 0.550) - (1.500)^2} = 120.706 \approx 120.71 \nonumber\]
\[b_0 = \frac {182.31 - (120.706 \times 1.500)} {6} = 0.209 \approx 0.21 \nonumber\]
La relación entre la señal y el analito, por lo tanto, es
\[S_{std} = 120.71 \times C_{std} + 0.21 \nonumber\]
Por ahora mantenemos dos decimales para que coincidan con el número de decimales en la señal. La curva de calibración resultante se muestra en la Figura 5.4.4 .
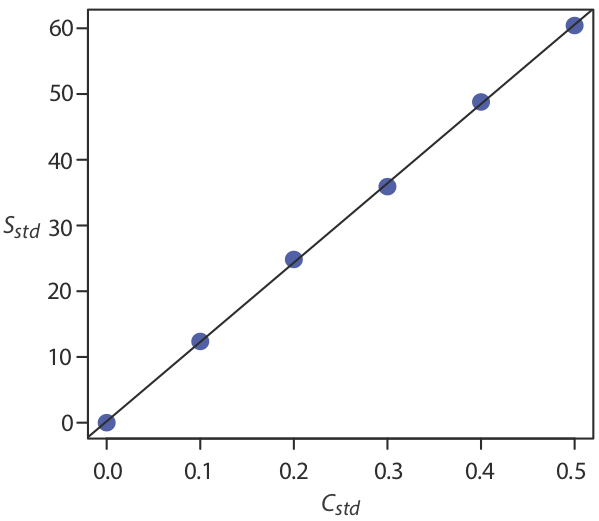
Incertidumbre en el análisis de regresión
Como se muestra en la Figura 5.4.4 , debido a errores indeterminados en la señal, la línea de regresión puede no pasar por el centro exacto de cada punto de datos. La desviación acumulada de nuestros datos de la línea de regresión, es decir, el error residual total, es proporcional a la incertidumbre en la regresión. Llamamos a esta incertidumbre la desviación estándar sobre la regresión, s r, que es igual a
\[s_r = \sqrt{\frac {\sum_{i = 1}^{n} \left( y_i - \hat{y}_i \right)^2} {n - 2}} \label{5.6}\]
donde y i es el i-ésimo valor experimental, y\(\hat{y}_i\) es el valor correspondiente predicho por la línea de regresión en la Ecuación\ ref {5.2}. Tenga en cuenta que el denominador de la Ecuación\ ref {5.6} indica que nuestro análisis de regresión tiene n — 2 grados de libertad — perdemos dos grados de libertad porque usamos dos parámetros, la pendiente y la intersección y, para calcular\(\hat{y}_i\).
¿Notó la similitud entre la desviación estándar sobre la regresión (Ecuación\ ref {5.6}) y la desviación estándar para una muestra (Ecuación 4.1.1)?
Una representación más útil de la incertidumbre en nuestro análisis de regresión es considerar el efecto de errores indeterminados en la pendiente, b 1, y la intersección y, b 0, que expresamos como desviaciones estándar.
Utilizamos estas desviaciones estándar para establecer intervalos de confianza para la pendiente esperada\(\beta_1\), y la intersección y esperada,\(\beta_0\)
\[\beta_1 = b_1 \pm t s_{b_1} \label{5.9}\]
\[\beta_0 = b_0 \pm t s_{b_0} \label{5.10}\]
donde seleccionamos t para un nivel de significancia de\(\alpha\) y para n — 2 grados de libertad. Tenga en cuenta que la Ecuación\ ref {5.9} y la Ecuación\ ref {5.10} no contienen un factor de\((\sqrt{n})^{-1}\) porque el intervalo de confianza se basa en una sola línea de regresión.
Calcular los intervalos de confianza del 95% para la pendiente y -intercepción a partir del Ejemplo 5.4.1 .
Solución
Comenzamos calculando la desviación estándar sobre la regresión. Para ello debemos calcular las señales predichas,\(\hat{y}_i\), utilizando la pendiente y -interceptar del Ejemplo 5.4.1 , y los cuadrados del error residual,\((y_i - \hat{y}_i)^2\). Usando el último estándar como ejemplo, encontramos que la señal predicha es
\[\hat{y}_6 = b_0 + b_1 x_6 = 0.209 + (120.706 \times 0.500) = 60.562 \nonumber\]
y que el cuadrado del error residual es
\[(y_i - \hat{y}_i)^2 = (60.42 - 60.562)^2 = 0.2016 \approx 0.202 \nonumber\]
En la siguiente tabla se muestran los resultados de las seis soluciones.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) |
\(\left( y_i - \hat{y}_i \right)^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (\ hat {y} _i\) ">0.209 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0437 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12.36 | \ (\ hat {y} _i\) ">12.280 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0064 |
| \ (x_i\) ">0.200 | \ (y_i\) ">24.83 | \ (\ hat {y} _i\) ">24.350 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.2304 |
| \ (x_i\) ">0.300 | \ (y_i\) ">35.91 | \ (\ hat {y} _i\) ">36.421 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.2611 |
| \ (x_i\) ">0.400 | \ (y_i\) ">48.79 | \ (\ hat {y} _i\) ">48.491 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0894 |
| \ (x_i\) ">0.500 | \ (y_i\) ">60.42 | \ (\ hat {y} _i\) ">60.562 | \ (\ izquierda (y_i -\ hat {y} _i\ derecha) ^2\) ">0.0202 |
Al sumar los datos en la última columna se obtiene el numerador de la Ecuación\ ref {5.6} como 0.6512; así, la desviación estándar sobre la regresión es
\[s_r = \sqrt{\frac {0.6512} {6 - 2}} = 0.4035 \nonumber\]
A continuación calculamos las desviaciones estándar para la pendiente y la intersección y usando la Ecuación\ ref {5.7} y la Ecuación\ ref {5.8}. Los valores para los términos de suma son del Ejemplo 5.4.1 .
\[s_{b_1} = \sqrt{\frac {6 \times (0.4035)^2} {(6 \times 0.550) - (1.500)^2}} = 0.965 \nonumber\]
\[s_{b_0} = \sqrt{\frac {(0.4035)^2 \times 0.550} {(6 \times 0.550) - (1.500)^2}} = 0.292 \nonumber\]
Finalmente, los intervalos de confianza del 95% (\(\alpha = 0.05\), 4 grados de libertad) para la pendiente y la intersección y son
\[\beta_1 = b_1 \pm ts_{b_1} = 120.706 \pm (2.78 \times 0.965) = 120.7 \pm 2.7 \nonumber\]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.209 \pm (2.78 \times 0.292) = 0.2 \pm 0.80 \nonumber\]
donde t (0.05, 4) del Apéndice 4 es 2.78. La desviación estándar sobre la regresión, s r, sugiere que la señal, S std, es precisa a un lugar decimal. Por esta razón reportamos la pendiente y la intersección y a un solo decimal.
Minimización de la incertidumbre en el modelo
Para minimizar la incertidumbre en la pendiente de una curva de calibración y -intercepción, espaciamos uniformemente nuestros estándares en un amplio rango de concentraciones de analitos. Un examen minucioso de la Ecuación\ ref {5.7} y la Ecuación\ ref {5.8} nos ayudan a apreciar por qué esto es cierto. Los denominadores de ambas ecuaciones incluyen el término\(\sum_{i = 1}^{n} (x_i - \overline{x}_i)^2\). Cuanto mayor sea el valor de este término, que logramos al aumentar el rango de x alrededor de su valor medio, menores serán las desviaciones estándar en la pendiente y la intersección y. Además, para minimizar la incertidumbre en la intersección y, ayuda a disminuir el valor del término\(\sum_{i = 1}^{n} x_i\) en la Ecuación\ ref {5.8}, lo cual se logra al incluir estándares para concentraciones más bajas del analito.
Obtención de la concentración de analito a partir de una ecuación de regresión
Una vez que tenemos nuestra ecuación de regresión, es fácil determinar la concentración de analito en una muestra. Cuando usamos una curva de calibración normal, por ejemplo, medimos la señal para nuestra muestra, S samp, y calculamos la concentración del analito, C A, usando la ecuación de regresión.
\[C_A = \frac {S_{samp} - b_0} {b_1} \label{5.11}\]
Lo menos obvio es cómo reportar un intervalo de confianza para C A que exprese la incertidumbre en nuestro análisis. Para calcular un intervalo de confianza necesitamos conocer la desviación estándar en la concentración del analito\(s_{C_A}\), que viene dada por la siguiente ecuación
donde m es el número de réplicas que utilizamos para establecer la señal promedio de la muestra, S samp, n es el número de estándares de calibración, S std es la señal promedio para la calibración estándares, y\(C_{std_1}\) y\(\overline{C}_{std}\) son las concentraciones individuales y medias para los estándares de calibración. Conociendo el valor de\(s_{C_A}\), el intervalo de confianza para la concentración del analito es
\[\mu_{C_A} = C_A \pm t s_{C_A} \nonumber\]
donde\(\mu_{C_A}\) está el valor esperado de C A en ausencia de errores determinados, y con el valor de t se basa en el nivel de confianza deseado y n — 2 grados de libertad.
La ecuación\ ref {5.12} se escribe en términos de un experimento de calibración. Aquí se da una forma más general de la ecuación, escrita en términos de x e y.
\[s_{x} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{Y} - \overline{y} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber\]
Un examen minucioso de la Ecuación\ ref {5.12} debería convencerte de que la incertidumbre en C A es menor cuando la señal promedio de la muestra\(\overline{S}_{samp}\),, es igual a la señal promedio para los estándares,\(\overline{S}_{std}\). Cuando sea práctico, debe planificar su curva de calibración para que S samp caiga en el medio de la curva de calibración. Para mayor información sobre estas ecuaciones de regresión ver (a) Miller, J. N. Analyst 1991, 116, 3—14; (b) Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986, pp. 126-127; (c) Analytical Methods Committee” Incertidumbres en las concentraciones estimadas a partir de experimentos de calibración”, Resumen Técnico de AMC, marzo de 2006.
Tres análisis replicados para una muestra que contiene una concentración desconocida de analito, valores de rendimiento para S samp de 29.32, 29.16 y 29.51 (unidades arbitrarias). Usando los resultados del Ejemplo 5.4.1 y Ejemplo 5.4.2 , determinar la concentración del analito, C A, y su intervalo de confianza del 95%.
Solución
La señal promedio,\(\overline{S}_{samp}\), es 29.33, que, usando la Ecuación\ ref {5.11} y la pendiente y la intersección y del Ejemplo 5.4.1 , da la concentración del analito como
\[C_A = \frac {\overline{S}_{samp} - b_0} {b_1} = \frac {29.33 - 0.209} {120.706} = 0.241 \nonumber\]
Para calcular la desviación estándar para la concentración del analito debemos determinar los valores para\(\overline{S}_{std}\) y para\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\). El primero es solo la señal promedio para los estándares de calibración, que, utilizando los datos de la Tabla 5.4.1 , es 30.385. El cálculo\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\) parece formidable, pero podemos simplificar su cálculo reconociendo que esta suma de cuadrados es el numerador en una ecuación de desviación estándar; así,
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (s_{C_{std}})^2 \times (n - 1) \nonumber\]
donde\(s_{C_{std}}\) está la desviación estándar para la concentración de analito en los estándares de calibración. Usando los datos en la Tabla 5.4.1 encontramos que\(s_{C_{std}}\) es 0.1871 y
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (0.1872)^2 \times (6 - 1) = 0.175 \nonumber\]
Sustituir valores conocidos en la ecuación\ ref {5.12} da
\[s_{C_A} = \frac {0.4035} {120.706} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(29.33 - 30.385)^2} {(120.706)^2 \times 0.175}} = 0.0024 \nonumber\]
Finalmente, el intervalo de confianza del 95% para 4 grados de libertad es
\[\mu_{C_A} = C_A \pm ts_{C_A} = 0.241 \pm (2.78 \times 0.0024) = 0.241 \pm 0.007 \nonumber\]
La Figura 5.4.5 muestra la curva de calibración con curvas que muestran el intervalo de confianza del 95% para C A.
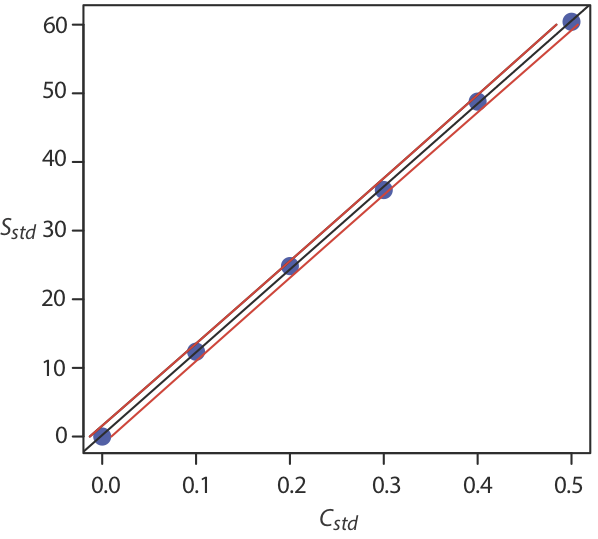
En una adición estándar determinamos la concentración del analito extrapolando la curva de calibración a la intersección x. En este caso el valor de C A es
\[C_A = x\text{-intercept} = \frac {-b_0} {b_1} \nonumber\]
y la desviación estándar en C A es
\[s_{C_A} = \frac {s_r} {b_1} \sqrt{\frac {1} {n} + \frac {(\overline{S}_{std})^2} {(b_1)^2 \sum_{i = 1}^{n}(C_{std_i} - \overline{C}_{std})^2}} \nonumber\]
donde n es el número de adiciones estándar (incluyendo la muestra sin estándar agregado), y\(\overline{S}_{std}\) es la señal promedio para los n estándares. Porque determinamos la concentración del analito por extrapolación, en lugar de por interpolación,\(s_{C_A}\) ya que el método de adiciones estándar generalmente es mayor que para una curva de calibración normal.
La Figura 5.4.2 muestra una curva de calibración normal para el análisis cuantitativo de Cu 2 +. Aquí se muestran los datos de la curva de calibración.
| [Cu 2+] (M) | Absorbancia |
|---|---|
| 0 | 0 |
| \(1.55 \times 10^{-3}\) | 0.050 |
| \(3.16 \times 10^{-3}\) | 0.093 |
| \(4.74 \times 10^{-3}\) | 0.143 |
| \(6.34 \times 10^{-3}\) | 0.188 |
| \(7.92 \times 10^{-3}\) | 0.236 |
Completar un análisis de regresión lineal para estos datos de calibración, reportando la ecuación de calibración y el intervalo de confianza del 95% para la pendiente y la intersección y. Si tres muestras replicadas dan una muestra de S de 0.114, ¿cuál es la concentración de analito en la muestra y su intervalo de confianza del 95%?
- Responder
-
Comenzamos configurando una tabla que nos ayude a organizar el cálculo
\(x_i\) \(y_i\) \(x_i y_i\) \(x_i^2\) \ (x_i\) ">0.000 \ (y_i\) ">0.000 \ (x_i y_i\) ">0.000 \ (x_i^2\) ">0.000 \ (x_i\) ">\(1.55 \times 10^{-3}\) \ (y_i\) ">0.050 \ (x_i y_i\) ">\(7.750 \times 10^{-5}\) \ (x_i^2\) ">\(2.403 \times 10^{-6}\) \ (x_i\) ">\(3.16 \times 10^{-3}\) \ (y_i\) ">0.093 \ (x_i y_i\) ">\(2.939 \times 10^{-4}\) \ (x_i^2\) ">\(9.986 \times 10^{-6}\) \ (x_i\) ">\(4.74 \times 10^{-3}\) \ (y_i\) ">0.143 \ (x_i y_i\) ">\(6.778 \times 10^{-4}\) \ (x_i^2\) ">\(2.247 \times 10^{-5}\) \ (x_i\) ">\(6.34 \times 10^{-3}\) \ (y_i\) ">0.188 \ (x_i y_i\) ">\(1.192 \times 10^{-3}\) \ (x_i^2\) ">\(4.020 \times 10^{-5}\) \ (x_i\) ">\(7.92 \times 10^{-3}\) \ (y_i\) ">0.236 \ (x_i y_i\) ">\(1.869 \times 10^{-3}\) \ (x_i^2\) ">\(6.273 \times 10^{-5}\) Sumando los valores en cada columna da
\[\sum_{i = 1}^{n} x_i = 2.371 \times 10^{-2} \quad \sum_{i = 1}^{n} y_i = 0.710 \quad \sum_{i = 1}^{n} x_i y_i = 4.110 \times 10^{-3} \quad \sum_{i = 1}^{n} x_i^2 = 1.378 \times 10^{-4} \nonumber\]
Cuando sustituimos estos valores en Ecuación\ ref {5.4} y Ecuación\ ref {5.5}, encontramos que la pendiente y la intersección y son
\[b_1 = \frac {6 \times (4.110 \times 10^{-3}) - (2.371 \times 10^{-2}) \times 0.710} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}) = 29.57 \nonumber\]
\[b_0 = \frac {0.710 - 29.57 \times (2.371 \times 10^{-2}} {6} = 0.0015 \nonumber\]
y que la ecuación de regresión es
\[S_{std} = 29.57 \times C_{std} + 0.0015 \nonumber\]
Para calcular los intervalos de confianza del 95%, primero necesitamos determinar la desviación estándar sobre la regresión. La siguiente tabla nos ayuda a organizar el cálculo.
\(x_i\) \(y_i\) \(\hat{y}_i\) \((y_i - \hat{y}_i)^2\) \ (x_i\) ">0.000 \ (y_i\) ">0.000 \ (\ hat {y} _i\) ">0.0015 \ ((y_i -\ hat {y} _i) ^2\) ">\(2.250 \times 10^{-6}\) \ (x_i\) ">\(1.55 \times 10^{-3}\) \ (y_i\) ">0.050 \ (\ hat {y} _i\) ">0.0473 \ ((y_i -\ hat {y} _i) ^2\) ">\(7.110 \times 10^{-6}\) \ (x_i\) ">\(3.16 \times 10^{-3}\) \ (y_i\) ">0.093 \ (\ hat {y} _i\) ">0.0949 \ ((y_i -\ hat {y} _i) ^2\) ">\(3.768 \times 10^{-6}\) \ (x_i\) ">\(4.74 \times 10^{-3}\) \ (y_i\) ">0.143 \ (\ hat {y} _i\) ">0.1417 \ ((y_i -\ hat {y} _i) ^2\) ">\(1.791 \times 10^{-6}\) \ (x_i\) ">\(6.34 \times 10^{-3}\) \ (y_i\) ">0.188 \ (\ hat {y} _i\) ">0.1890 \ ((y_i -\ hat {y} _i) ^2\) ">\(9.483 \times 10^{-6}\) \ (x_i\) ">\(7.92 \times 10^{-3}\) \ (y_i\) ">0.236 \ (\ hat {y} _i\) ">0.2357 \ ((y_i -\ hat {y} _i) ^2\) ">\(9.339 \times 10^{-6}\) Sumando los datos en la última columna da el numerador de Ecuación\ ref {5.6} as\(1.596 \times 10^{-5}\). La desviación estándar sobre la regresión, por lo tanto, es
\[s_r = \sqrt{\frac {1.596 \times 10^{-5}} {6 - 2}} = 1.997 \times 10^{-3} \nonumber\]
A continuación, necesitamos calcular las desviaciones estándar para la pendiente y la intersección y usando la Ecuación\ ref {5.7} y la Ecuación\ ref {5.8}.
\[s_{b_1} = \sqrt{\frac {6 \times (1.997 \times 10^{-3})^2} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}} = 0.3007 \nonumber\]
\[s_{b_0} = \sqrt{\frac {(1.997 \times 10^{-3})^2 \times (1.378 \times 10^{-4})} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}} = 1.441 \times 10^{-3} \nonumber\]
y utilizarlos para calcular los intervalos de confianza del 95% para la pendiente y la intersección y
\[\beta_1 = b_1 \pm ts_{b_1} = 29.57 \pm (2.78 \times 0.3007) = 29.57 \text{ M}^{-1} \pm 0.84 \text{ M}^{-1} \nonumber\]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.0015 \pm (2.78 \times 1.441 \times 10^{-3}) = 0.0015 \pm 0.0040 \nonumber\]
Con una muestra promedio de S de 0.114, la concentración de analito, C A, es
\[C_A = \frac {S_{samp} - b_0} {b_1} = \frac {0.114 - 0.0015} {29.57 \text{ M}^{-1}} = 3.80 \times 10^{-3} \text{ M} \nonumber\]
La desviación estándar en C A es
\[s_{C_A} = \frac {1.997 \times 10^{-3}} {29.57} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(0.114 - 0.1183)^2} {(29.57)^2 \times (4.408 \times 10^{-5})}} = 4.778 \times 10^{-5} \nonumber\]
y el intervalo de confianza del 95% es
\[\mu = C_A \pm t s_{C_A} = 3.80 \times 10^{-3} \pm \{2.78 \times (4.778 \times 10^{-5})\} \nonumber\]
\[\mu = 3.80 \times 10^{-3} \text{ M} \pm 0.13 \times 10^{-3} \text{ M} \nonumber\]
Evaluación de un modelo de regresión lineal
Nunca se debe aceptar el resultado de un análisis de regresión lineal sin evaluar la validez del modelo. Quizás la forma más sencilla de evaluar un análisis de regresión es examinar los errores residuales. Como vimos anteriormente, el error residual para un único estándar de calibración, r i, es
\[r_i = (y_i - \hat{y}_i) \nonumber\]
Si el modelo de regresión es válido, entonces los errores residuales deben distribuirse aleatoriamente alrededor de un error residual promedio de cero, sin tendencia aparente hacia errores residuales menores o mayores (Figura 5.4.6 a). Tendencias como las de la Figura 5.4.6 b y la Figura 5.4.6 c proporcionan evidencia de que al menos uno de los supuestos del modelo es incorrecto. Por ejemplo, una tendencia hacia errores residuales mayores a concentraciones más altas, Figura 5.4.6 b, sugiere que los errores indeterminados que afectan a la señal no son independientes de la concentración del analito. En la Figura 5.4.6 c, los errores residuales no son aleatorios, lo que sugiere que no podemos modelar los datos usando una relación de línea recta. Los métodos de regresión para estos dos últimos casos se discuten en las siguientes secciones.
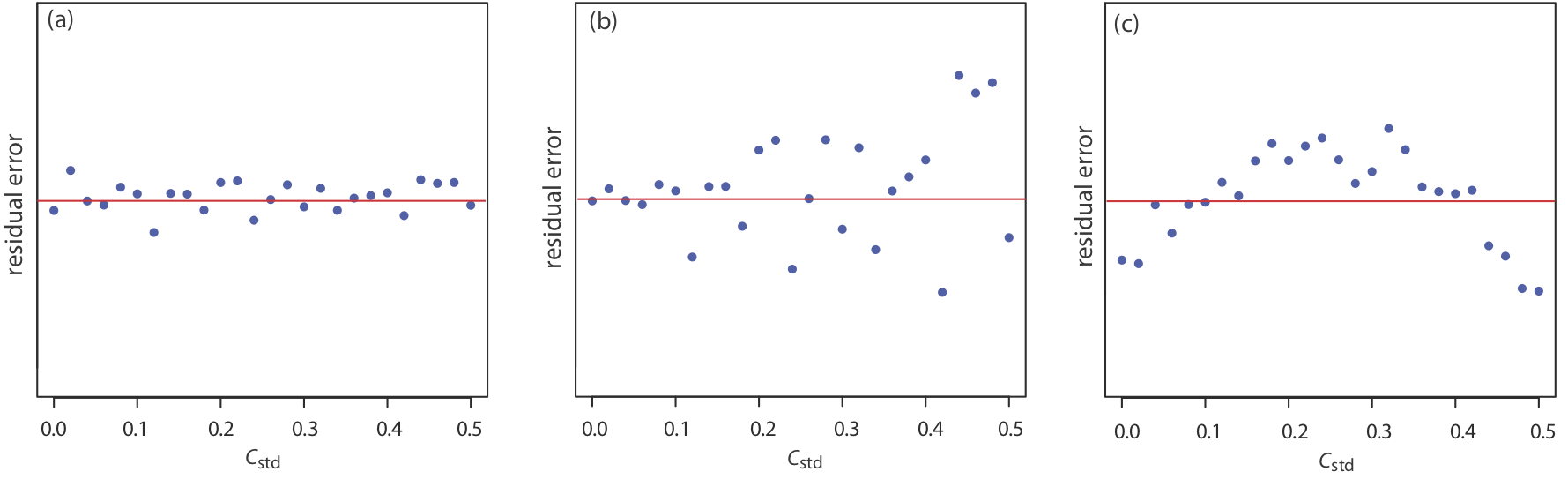
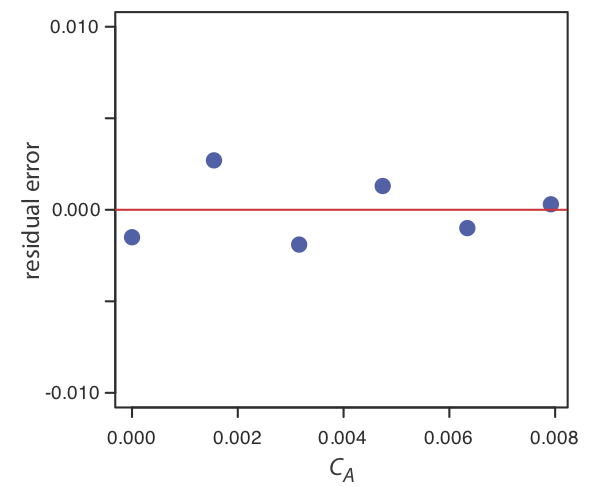
Usando tus resultados del Ejercicio 5.4.1 , construye una gráfica residual y explica su significado.
- Responder
-
Para crear una gráfica residual, necesitamos calcular el error residual para cada estándar. La siguiente tabla contiene la información relevante.
\(x_i\) \(y_i\) \(\hat{y}_i\) \(y_i - \hat{y}_i\) \ (x_i\) ">0.000 \ (y_i\) ">0.000 \ (\ hat {y} _i\) ">0.0015 \ (y_i -\ hat {y} _i\) ">—0.0015 \ (x_i\) ">\(1.55 \times 10^{-3}\) \ (y_i\) ">0.050 \ (\ hat {y} _i\) ">0.0473 \ (y_i -\ hat {y} _i\) ">0.0027 \ (x_i\) ">\(3.16 \times 10^{-3}\) \ (y_i\) ">0.093 \ (\ hat {y} _i\) ">0.0949 \ (y_i -\ hat {y} _i\) ">—0.0019 \ (x_i\) ">\(4.74 \times 10^{-3}\) \ (y_i\) ">0.143 \ (\ hat {y} _i\) ">0.1417 \ (y_i -\ hat {y} _i\) ">0.0013 \ (x_i\) ">\(6.34 \times 10^{-3}\) \ (y_i\) ">0.188 \ (\ hat {y} _i\) ">0.1890 \ (y_i -\ hat {y} _i\) ">—0.0010 \ (x_i\) ">\(7.92 \times 10^{-3}\) \ (y_i\) ">0.236 \ (\ hat {y} _i\) ">0.2357 \ (y_i -\ hat {y} _i\) ">0.0003 La siguiente figura muestra una gráfica de los errores residuales resultantes. Los errores residuales aparecen aleatorios, aunque sí alternan en signo, y que no muestran ninguna dependencia significativa de la concentración del analito. En conjunto, estas observaciones sugieren que nuestro modelo de regresión es apropiado.
Regresión lineal ponderada con errores en y
Nuestro tratamiento de la regresión lineal hasta este punto asume que los errores indeterminados que afectan a y son independientes del valor de x. Si esta suposición es falsa, como es el caso de los datos de la Figura 5.4.6 b, entonces debemos incluir la varianza para cada valor de y en nuestra determinación de la intersección y, b 0, y la pendiente, b 1; así
\[b_0 = \frac {\sum_{i = 1}^{n} w_i y_i - b_1 \sum_{i = 1}^{n} w_i x_i} {n} \label{5.13}\]
donde w i es un factor de ponderación que da cuenta de la varianza en y i
\[w_i = \frac {n (s_{y_i})^{-2}} {\sum_{i = 1}^{n} (s_{y_i})^{-2}} \label{5.15}\]
y\(s_{y_i}\) es la desviación estándar para y i. En una regresión lineal ponderada, la contribución de cada par xy a la línea de regresión es inversamente proporcional a la precisión de y i; es decir, cuanto más preciso sea el valor de y, mayor será su contribución al regresión.
Aquí se muestran datos para una estandarización externa en la que s std es la desviación estándar para la determinación de tres réplicas de la señal. Se trata de los mismos datos utilizados en el Ejemplo 5.4.1 con información adicional sobre las desviaciones estándar en la señal.
| \(C_{std}\)(unidades arbitrarias) | \(S_{std}\)(unidades arbitrarias) | \(s_{std}\) |
|---|---|---|
| \ (C_ {std}\) (unidades arbitrarias) ">0.000 | \ (S_ {std}\) (unidades arbitrarias) ">0.00 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.100 | \ (S_ {std}\) (unidades arbitrarias) ">12.36 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.200 | \ (S_ {std}\) (unidades arbitrarias) ">24.83 | \ (s_ {std}\) ">0.07 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.300 | \ (S_ {std}\) (unidades arbitrarias) ">35.91 | \ (s_ {std}\) ">0.13 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.400 | \ (S_ {std}\) (unidades arbitrarias) ">48.79 | \ (s_ {std}\) ">0.22 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.500 | \ (S_ {std}\) (unidades arbitrarias) ">60.42 | \ (s_ {std}\) ">0.33 |
Determinar la ecuación de la curva de calibración usando una regresión lineal ponderada. Al trabajar a través de este ejemplo, recuerde que x corresponde a C std, y que y corresponde a S std.
Solución
Comenzamos configurando una tabla para ayudar en el cálculo de los factores de ponderación.
| \(C_{std}\)(unidades arbitrarias) | \(S_{std}\)(unidades arbitrarias) | \(s_{std}\) | \((s_{y_i})^{-2}\) | \(w_i\) |
|---|---|---|---|---|
| \ (C_ {std}\) (unidades arbitrarias) ">0.000 | \ (S_ {std}\) (unidades arbitrarias) ">0.00 | \ (s_ {std}\) ">0.02 | \ ((s_ {y_i}) ^ {-2}\) ">2500.00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.100 | \ (S_ {std}\) (unidades arbitrarias) ">12.36 | \ (s_ {std}\) ">0.02 | \ ((s_ {y_i}) ^ {-2}\) ">250,00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.200 | \ (S_ {std}\) (unidades arbitrarias) ">24.83 | \ (s_ {std}\) ">0.07 | \ ((s_ {y_i}) ^ {-2}\) ">204.08 | \ (w_i\) ">0.2313 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.300 | \ (S_ {std}\) (unidades arbitrarias) ">35.91 | \ (s_ {std}\) ">0.13 | \ ((s_ {y_i}) ^ {-2}\) ">59.17 | \ (w_i\) ">0.0671 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.400 | \ (S_ {std}\) (unidades arbitrarias) ">48.79 | \ (s_ {std}\) ">0.22 | \ ((s_ {y_i}) ^ {-2}\) ">20.66 | \ (w_i\) ">0.0234 |
| \ (C_ {std}\) (unidades arbitrarias) ">0.500 | \ (S_ {std}\) (unidades arbitrarias) ">60.42 | \ (s_ {std}\) ">0.33 | \ ((s_ {y_i}) ^ {-2}\) ">9.18 | \ (w_i\) ">0.0104 |
Sumando los valores en la cuarta columna da
\[\sum_{i = 1}^{n} (s_{y_i})^{-2} \nonumber\]
que utilizamos para calcular los pesos individuales en la última columna. Como comprobación de sus cálculos, la suma de los pesos individuales debe ser igual al número de estándares de calibración, n. La suma de las entradas en la última columna es de 6.0000, así que todo está bien. Después de calcular los pesos individuales, utilizamos una segunda tabla para ayudar en el cálculo de los cuatro términos de suma en la Ecuación\ ref {5.13} y Ecuación\ ref {5.14}.
| \(x_i\) | \(y_i\) | \(w_i\) | \(w_i x_i\) | \(w_i y_i\) | \(w_i x_i^2\) | \(w_i x_i y_i\) |
|---|---|---|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0.0000 | \ (w_i y_i\) ">0.0000 | \ (w_i x_i^2\) ">0.0000 | \ (w_i x_i y_i\) ">0.0000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12.36 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0.2834 | \ (w_i y_i\) ">35.0270 | \ (w_i x_i^2\) ">0.0283 | \ (w_i x_i y_i\) ">3.5027 |
| \ (x_i\) ">0.200 | \ (y_i\) ">24.83 | \ (w_i\) ">0.2313 | \ (w_i x_i\) ">0.0463 | \ (w_i y_i\) ">5.7432 | \ (w_i x_i^2\) ">0.0093 | \ (w_i x_i y_i\) ">1.1486 |
| \ (x_i\) ">0.300 | \ (y_i\) ">35.91 | \ (w_i\) ">0.0671 | \ (w_i x_i\) ">0.0201 | \ (w_i y_i\) ">2.4096 | \ (w_i x_i^2\) ">0.0060 | \ (w_i x_i y_i\) ">0.7229 |
| \ (x_i\) ">0.400 | \ (y_i\) ">48.79 | \ (w_i\) ">0.0234 | \ (w_i x_i\) ">0.0094 | \ (w_i y_i\) ">1.1417 | \ (w_i x_i^2\) ">0.0037 | \ (w_i x_i y_i\) ">0.4567 |
| \ (x_i\) ">0.500 | \ (y_i\) ">60.42 | \ (w_i\) ">0.0104 | \ (w_i x_i\) ">0.0052 | \ (w_i y_i\) ">0.6284 | \ (w_i x_i^2\) ">0.0026 | \ (w_i x_i y_i\) ">0.3142 |
Sumando los valores en las últimas cuatro columnas da
\[\sum_{i = 1}^{n} w_i x_i = 0.3644 \quad \sum_{i = 1}^{n} w_i y_i = 44.9499 \quad \sum_{i = 1}^{n} w_i x_i^2 = 0.0499 \quad \sum_{i = 1}^{n} w_i x_i y_i = 6.1451 \nonumber\]
Sustituyendo estos valores en la Ecuación\ ref {5.13} y la Ecuación\ ref {5.14} da la pendiente estimada y la intersección y estimada como
\[b_1 = \frac {(6 \times 6.1451) - (0.3644 \times 44.9499)} {(6 \times 0.0499) - (0.3644)^2} = 122.985 \nonumber\]
\[b_0 = \frac{44.9499 - (122.985 \times 0.3644)} {6} = 0.0224 \nonumber\]
La ecuación de calibración es
\[S_{std} = 122.98 \times C_{std} + 0.2 \nonumber\]
La Figura 5.4.7 muestra la curva de calibración para la regresión ponderada y la curva de calibración para la regresión no ponderada en el Ejemplo 5.4.1 . Aunque las dos curvas de calibración son muy similares, existen ligeras diferencias en la pendiente y en la intersección y. Lo más notable es que la intersección y para la regresión lineal ponderada está más cerca del valor esperado de cero. Debido a que la desviación estándar para la señal, S std, es menor para concentraciones más pequeñas de analito, C std, una regresión lineal ponderada da más énfasis a estos estándares, permitiendo una mejor estimación de la y -interceptar.
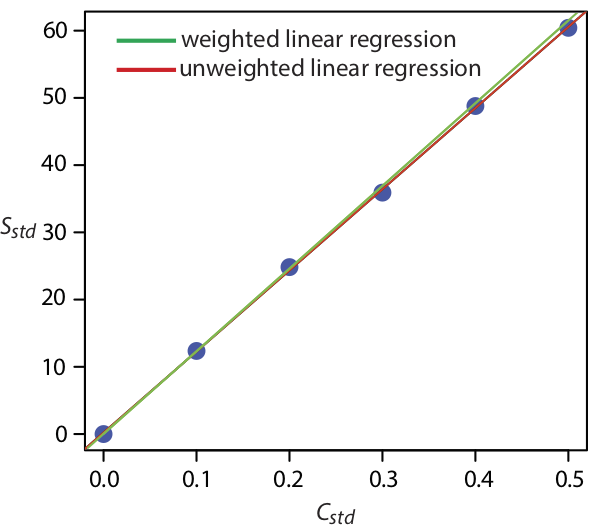
Las ecuaciones para calcular los intervalos de confianza para la pendiente, la intersección y y la concentración de analito cuando se utiliza una regresión lineal ponderada no son tan fáciles de definir como para una regresión lineal no ponderada [Bonate, P. J. Anal. Chem. 1993, 65, 1367—1372]. El intervalo de confianza para la concentración del analito, sin embargo, está en su valor óptimo cuando la señal del analito está cerca del centroide ponderado, y c, de la curva de calibración.
\[y_c = \frac {1} {n} \sum_{i = 1}^{n} w_i x_i \nonumber\]
Regresión lineal ponderada con errores en x e y
Si eliminamos nuestra suposición de que los errores indeterminados que afectan a una curva de calibración están presentes solo en la señal (y), entonces también debemos factorizar en el modelo de regresión los errores indeterminados que afectan la concentración del analito en los patrones de calibración (x). La solución para la línea de regresión resultante es computacionalmente más involucrada que la de las líneas de regresión no ponderadas o ponderadas. Si bien no consideraremos los detalles en este libro de texto, debe ser consciente de que descuidar la presencia de errores indeterminados en x puede sesgar los resultados de una regresión lineal.
Véase, por ejemplo, Comité de Métodos Analíticos, “Ajuste de una relación funcional lineal a datos con error en ambas variables”, Resumen Técnico AMC, marzo de 2002), así como Recursos Adicionales de este capítulo.
Regresión Curvilínea y Multivariada
Un modelo de regresión lineal, a pesar de su aparente complejidad, es la relación funcional más simple entre dos variables. ¿Qué hacemos si nuestra curva de calibración es curvilínea, es decir, si es una línea curva en lugar de una línea recta? Un enfoque es intentar transformar los datos en una línea recta. De esta manera se han utilizado logaritmos, exponenciales, recíprocos, raíces cuadradas y funciones trigonométricas. Una gráfica de log (y) versus x es un ejemplo típico. Tales transformaciones no están exentas de complicaciones, de las cuales la más obvia es que los datos con una varianza uniforme en y no mantendrán esa varianza uniforme después de que se transforme.
Cabe señalar que el término “lineal” no significa una línea recta. Una función lineal puede contener más de un término aditivo, pero cada término tiene uno y solo un parámetro multiplicativo ajustable. La función
\[y = ax + bx^2 \nonumber\]
es un ejemplo de una función lineal porque los términos x y x 2 incluyen cada uno un único parámetro multiplicativo, a y b, respectivamente. La función
\[y = x^b \nonumber\]
es no lineal porque b no es un parámetro multiplicativo; es, en cambio, una potencia. Es por esto que puedes usar regresión lineal para ajustar una ecuación polinómica a tus datos.
A veces es posible transformar una función no lineal en una función lineal. Por ejemplo, tomar el log de ambos lados de la función no lineal anterior da una función lineal.
\[\log(y) = b \log(x) \nonumber\]
Otro enfoque para desarrollar un modelo de regresión lineal es ajustar una ecuación polinómica a los datos, como\(y = a + b x + c x^2\). Puede usar regresión lineal para calcular los parámetros a, b y c, aunque las ecuaciones son diferentes a las de la regresión lineal de una línea recta. Si no puede ajustar sus datos usando una sola ecuación polinómica, es posible ajustar ecuaciones polinómicas separadas a segmentos cortos de la curva de calibración. El resultado es una curva de calibración continua única conocida como función spline.
Para obtener detalles sobre la regresión curvilínea, véase (a) Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986; (b) Deming, S. N.; Morgan, S. L. Experimental Design: A Chemometric Approach, Elsevier: Amsterdam, 1987.
Los modelos de regresión de este capítulo se aplican únicamente a funciones que contienen una sola variable independiente, como una señal que depende de la concentración del analito. En presencia de un interferente, sin embargo, la señal puede depender de las concentraciones tanto del analito como del interferente
\[S = k_A C_A + k_I CI + S_{reag} \nonumber\]
donde k I es la sensibilidad del interferente y C I es la concentración del interferente. Las curvas de calibración multivariadas se preparan usando estándares que contienen cantidades conocidas tanto del analito como del interferente, y se modelan mediante regresión multivariante.
Ver Beebe, K. R.; Kowalski, B. R. Anal. Chem. 1987, 59, 1007A-1017A. para más detalles, y consulte los Recursos Adicionales de este capítulo para obtener más información sobre regresión lineal con errores en ambas variables, regresión curvilínea y regresión multivariada.


