10.2: Espectroscopia basada en absorción

En la espectroscopia de absorción un haz de radiación electromagnética pasa a través de una muestra. Gran parte de la radiación pasa a través de la muestra sin pérdida de intensidad. A longitudes de onda seleccionadas, sin embargo, la intensidad de la radiación se atenúa. Este proceso de atenuación se llama absorción.

Espectros de absorción

Hay dos requisitos generales para la absorción de radiación electromagnética por parte de un analito. Primero, debe existir un mecanismo por el cual el campo eléctrico o campo magnético de la radiación interactúe con el analito. Para la radiación ultravioleta y visible, la absorción de un fotón cambia la energía de los electrones de valencia del analito. La energía vibratoria de un enlace se ve alterada por la absorción de la radiación infrarroja.

La Figura 10.1.3 proporciona una lista de los tipos de transiciones atómicas y moleculares asociadas con diferentes tipos de radiación electromagnética.

El segundo requisito es que la energía del fotón,\(h \nu\), debe igualar exactamente la diferencia de energía,\(\Delta E\), entre dos de los estados energéticos cuantificados del analito. La Figura 10.1.4 muestra una vista simplificada de la absorción de un fotón, lo cual es útil porque enfatiza que la energía del fotón debe coincidir con la diferencia de energía entre un estado de menor energía y un estado de mayor energía. Lo que falta, sin embargo, es información sobre qué tipos de estados energéticos están involucrados, qué transiciones entre estados energéticos es probable que ocurran, y la aparición del espectro resultante.

Podemos usar el diagrama de nivel de energía en la Figura 10.2.1 para explicar un espectro de absorbancia. Las líneas etiquetadas E ₀ y _E1 representan el estado electrónico de tierra (más bajo) del analito y su primer estado electrónico excitado. Superpuesta en cada nivel de energía electrónica hay una serie de líneas que representan los niveles de energía vibratoria.

Figura 10.2.1 . Diagrama que muestra dos niveles de energía electrónica (E ₀ y E ₁), cada uno con cinco niveles de energía vibratoria\(\nu_{0-4}\). La absorción de la radiación ultravioleta y visible (mostrada por las flechas azules) conduce a un cambio en los niveles de energía electrónica del analito y, posiblemente, a un cambio en la energía vibratoria también. Un cambio en la energía vibratoria sin un cambio en los niveles de energía electrónica ocurre con la absorción de la radiación infrarroja (mostrada por las flechas rojas).

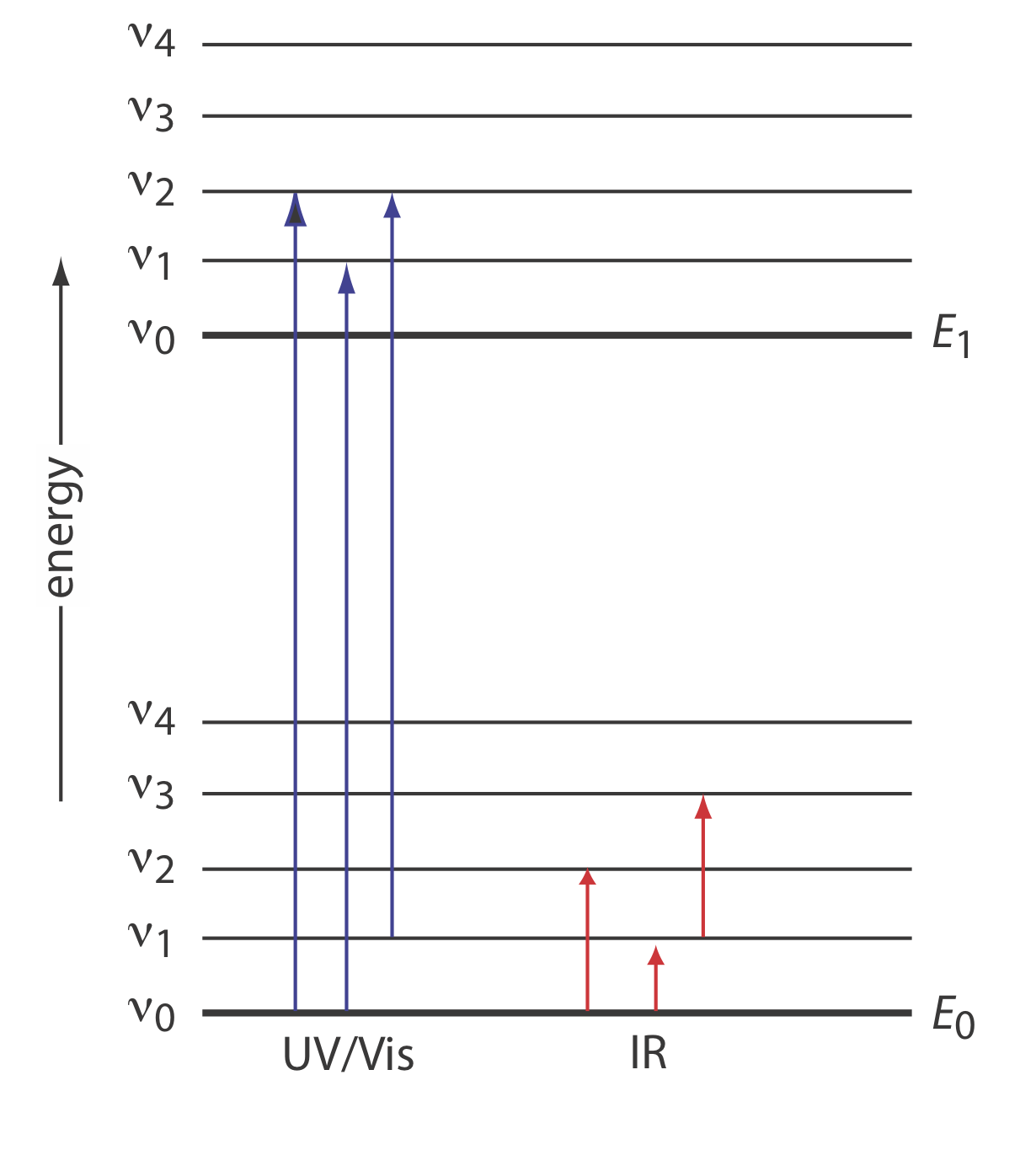
Espectros infrarrojos para moléculas e iones poliatómicos

La energía de la radiación infrarroja produce un cambio en la energía vibratoria de una molécula o de un ion poliatómico, pero no es suficiente para efectuar un cambio en su energía electrónica. Como se muestra en la Figura 10.2.1 , se cuantifican los niveles de energía vibracional; es decir, una molécula o ion poliatómico tiene solo ciertas energías vibracionales discretas. La energía para un modo vibratorio permitido,\(E_{\nu}\), es

\[E_{\nu}=\nu+\frac{1}{2} h \nu_{0} \nonumber\]

donde\(\nu\) está el número cuántico vibracional, que tiene valores de 0, 1, 2,..., y\(\nu_0\) es la frecuencia vibracional fundamental del enlace. El valor de\(\nu_0\), que está determinado por la fuerza de la unión y por la masa en cada extremo del enlace, es una propiedad característica de un enlace. Por ejemplo, un enlace simple carbono-carbono (C—C) absorbe la radiación infrarroja a una energía menor que un doble enlace carbono-carbono (C=C) porque un enlace sencillo es más débil que un doble enlace.

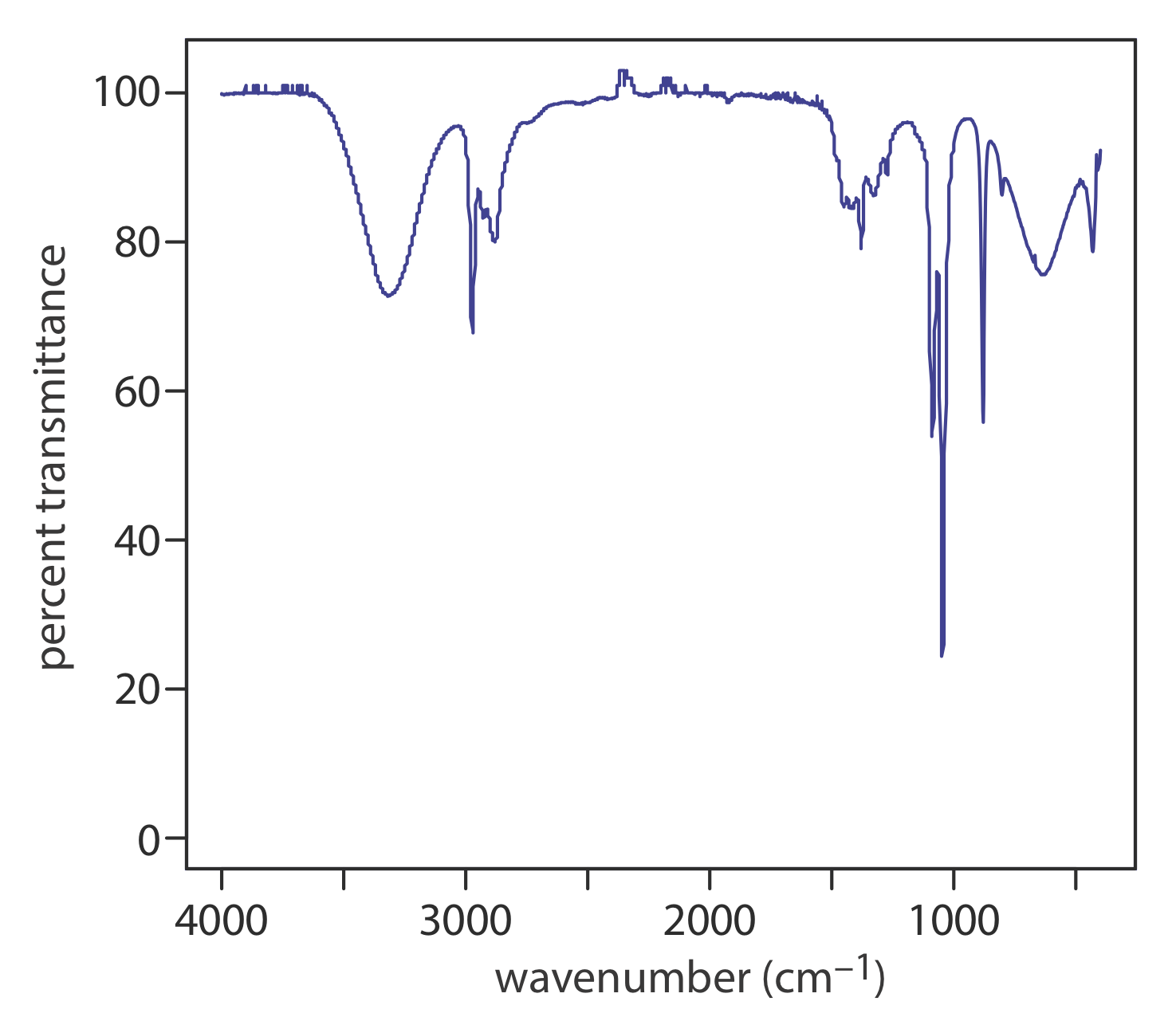
A temperatura ambiente la mayoría de las moléculas se encuentran en su estado vibratorio terrestre (\(\nu = 0\)). Una transición del estado vibratorio del suelo al primer estado vibracional excitado (\(\nu = 1\)) requiere la absorción de un fotón con una energía de\(h \nu_0\). Transiciones en las que\(\Delta \nu = \pm 1\) dan lugar a las líneas de absorción fundamentales. Las líneas de absorción más débiles, llamadas armónicas, resultan de transiciones en las que\(\Delta \nu\) es ±2 o ±3. El número de modos vibracionales normales posibles para una molécula lineal es 3 N — 5, y para una molécula no lineal es 3 N — 6, donde N es el número de átomos en la molécula. No es sorprendente que los espectros infrarrojos a menudo muestren un número considerable de bandas de absorción. Incluso una molécula relativamente simple, como el etanol (C ₂ H ₆ O), por ejemplo, tiene\(3 \times 9 - 6\), o 21 posibles modos normales de vibración, aunque no todos estos modos vibracionales dan lugar a una absorción. El espectro IR para etanol se muestra en la Figura 10.2.2 .

¿Por qué una molécula no lineal tiene 3 N — 6 modos de vibración? Considerar una molécula de metano, CH ₄. Cada uno de los cinco átomos del metano puede moverse en una de tres direcciones (x, y y z) para un total de\(5 \times 3 = 15\) diferentes formas en las que los átomos de la molécula pueden moverse. Una molécula puede moverse de tres maneras: puede moverse de un lugar a otro, lo que llamamos movimiento traslacional; puede girar alrededor de un eje, al que llamamos movimiento rotacional; y sus enlaces pueden estirarse y doblarse, lo que llamamos movimiento vibracional. Debido a que toda la molécula puede moverse en las direcciones x, y y z, tres de los 15 movimientos diferentes del metano son traslacionales. Además, la molécula puede rotar alrededor de sus ejes x, y y z, lo que representa tres formas adicionales de movimiento. Esto deja 15 — 3 — 3 = 9 modos vibracionales. Una molécula lineal, como el CO ₂, tiene 3 N — 5 modos vibracionales porque puede girar alrededor de solo dos ejes.

Figura 10.2.2 . Espectro infrarrojo del etanol.

Espectros UV/Vis para Moléculas e Iones

Los electrones de valencia en moléculas orgánicas e iones poliatómicos, tales como\(\text{CO}_3^{2-}\), ocupan orbitales moleculares cuantificados de enlace sigma (\(\sigma\)), enlace pi (\(\pi\)) y no enlace (n) orbitales moleculares (MO). Los orbitales moleculares no ocupados sigma antibonding (\(\sigma^*\)) y pi antibonding (\(\pi^*\)) son ligeramente más altos en energía. Debido a que la diferencia de energía entre los MO ocupados de mayor energía y los MO desocupados de menor energía corresponde a la radiación ultravioleta y visible, es posible la absorción de un fotón.

Cuatro tipos de transiciones entre los niveles de energía cuantificados representan la mayoría de los espectros moleculares UV/Vis. La Tabla 10.2.1 enumera los rangos de longitud de onda aproximados para estas transiciones, así como una lista parcial de enlaces, grupos funcionales o moléculas responsables de estas transiciones. De estas transiciones, las más importantes son\(n \rightarrow \pi^*\) y\(\pi \rightarrow \pi^*\) porque involucran grupos funcionales importantes que son característicos de muchos analitos y porque las longitudes de onda son fácilmente accesibles. Los enlaces y grupos funcionales que dan lugar a la absorción de radiación ultravioleta y visible se denominan cromóforos.

Tabla 10.2.1 . Transiciones electrónicas que involucran orbitales n\(\sigma\), y\(\pi\) moleculares

transición	rango de longitud de onda	ejemplos
\(\sigma \rightarrow \sigma^*\)	<200 nm	C—C, C—H
\(n \rightarrow \sigma^*\)	160—260 nm	H 2 O, CH 3 OH, CH 3 Cl
\(\pi \rightarrow \pi^*\)	200—500 nm	C=C, C=O, C=N, C=C
\(n \rightarrow \pi^*\)	250—600 nm	C=O, C=N, N=N, N=O

Muchos iones de metales de transición, como Cu ^{2 +} y Co ^{2 +}, forman soluciones coloridas porque el ion metálico absorbe la luz visible. Las transiciones que dan lugar a esta absorción son electrones de valencia en los d -orbitales del ión metálico. Para un ion metálico libre, los cinco d -orbitales son de igual energía. Sin embargo, en presencia de un ligando complejante o molécula solvente, los d-orbitales se dividieron en dos o más grupos que difieren en energía. Por ejemplo, en un complejo octaédrico de\(\text{Cu(H}_2\text{O)}_6^{2+}\) las seis moléculas de agua perturban los d-orbitales en los dos grupos mostrados en la Figura 10.2.3 . \(d \rightarrow d\)Las transiciones resultantes para los iones de metales de transición son relativamente débiles.

Figura 10.2.3 . División de los d -orbitales en un campo octaédrico.

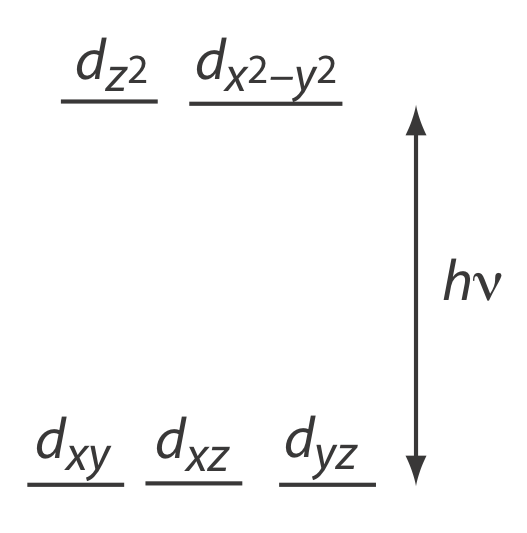
Una fuente más importante de absorción UV/Vis para los complejos inorgánicos metal-ligando es la transferencia de carga, en la que la absorción de un fotón produce un estado excitado en el que hay transferencia de un electrón desde el metal, M, al ligando, L.

\[M-L+h \nu \rightarrow\left(M^{+}-L^{-}\right)^{*} \nonumber\]

La absorción de transferencia de carga es importante porque produce absorbancias muy grandes. Un ejemplo importante de un complejo de transferencia de carga es el de o -fenantrolina con Fe ^{2 +}, cuyo espectro UV/Vis se muestra en la Figura 10.2.4 . También es posible la absorción de transferencia de carga en la que un electrón se mueve del ligando al metal.

¿Por qué es deseable una mayor absorbancia? Un método analítico es más sensible si una concentración menor de analito da una señal mayor.

Figura 10.2.4 . Espectro UV/vis para el complejo metal-ligando\(\text{Fe(phen)}_3^{2+}\), donde phen es el ligando o-fenantrolina.

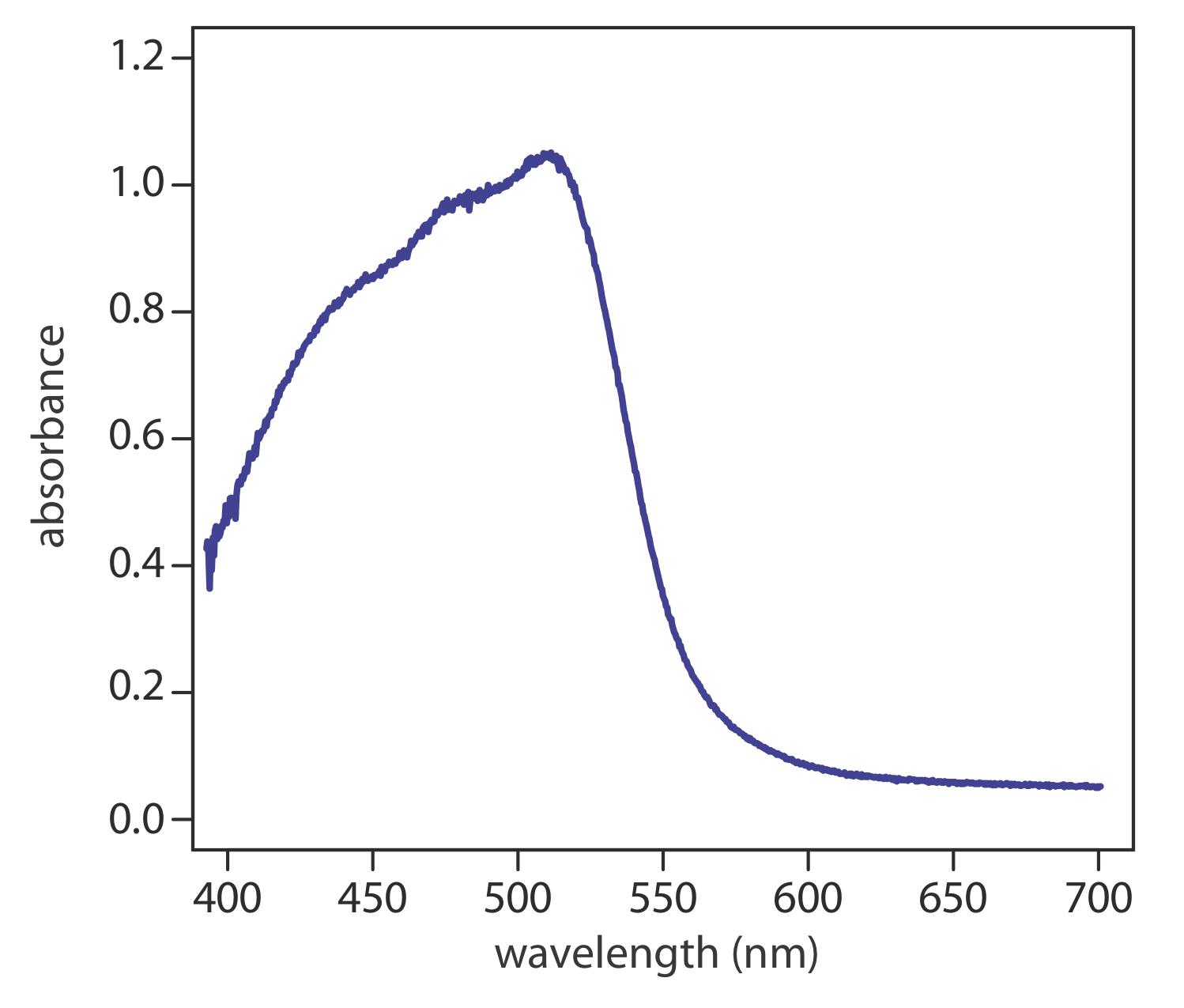
La comparación del espectro IR en la Figura 10.2.2 con el espectro UV/Vis en la Figura 10.2.4 nos muestra que las bandas de absorción UV/Vis suelen ser significativamente más amplias que las de absorción IR. Podemos usar Figure 10.2.1 para explicar por qué esto es cierto. Cuando una especie absorbe radiación UV/Vis, la transición entre los niveles de energía electrónica también puede incluir una transición entre los niveles de energía vibratoria. El resultado es una serie de bandas de absorción estrechamente espaciadas que se fusionan para formar una sola banda de absorción ancha.

Espectros UV/Vis para Átomos

La energía de la radiación electromagnética ultravioleta y visible es suficiente para provocar un cambio en la configuración electrónica de valencia de un átomo. El sodio, por ejemplo, tiene un solo electrón de valencia en su orbital atómico de 3 s. Como se muestra en la Figura 10.2.5 , también existen orbitales atómicos desocupados de mayor energía.

El diagrama de nivel de energía del caparazón de valencia en la Figura 10.2.5 podría parecerte extraño porque muestra que los orbitales de 3 p se dividen en dos grupos de energía ligeramente diferente. Las razones de esta división no son importantes en el contexto de nuestro tratamiento de la absorción atómica. Para mayor información sobre los motivos de esta división, consulte los recursos adicionales del capítulo.

Figura 10.2.5 . Diagrama de nivel de energía de concha de valencia para sodio. Se muestran las longitudes de onda (en números de onda) correspondientes a varias transiciones.

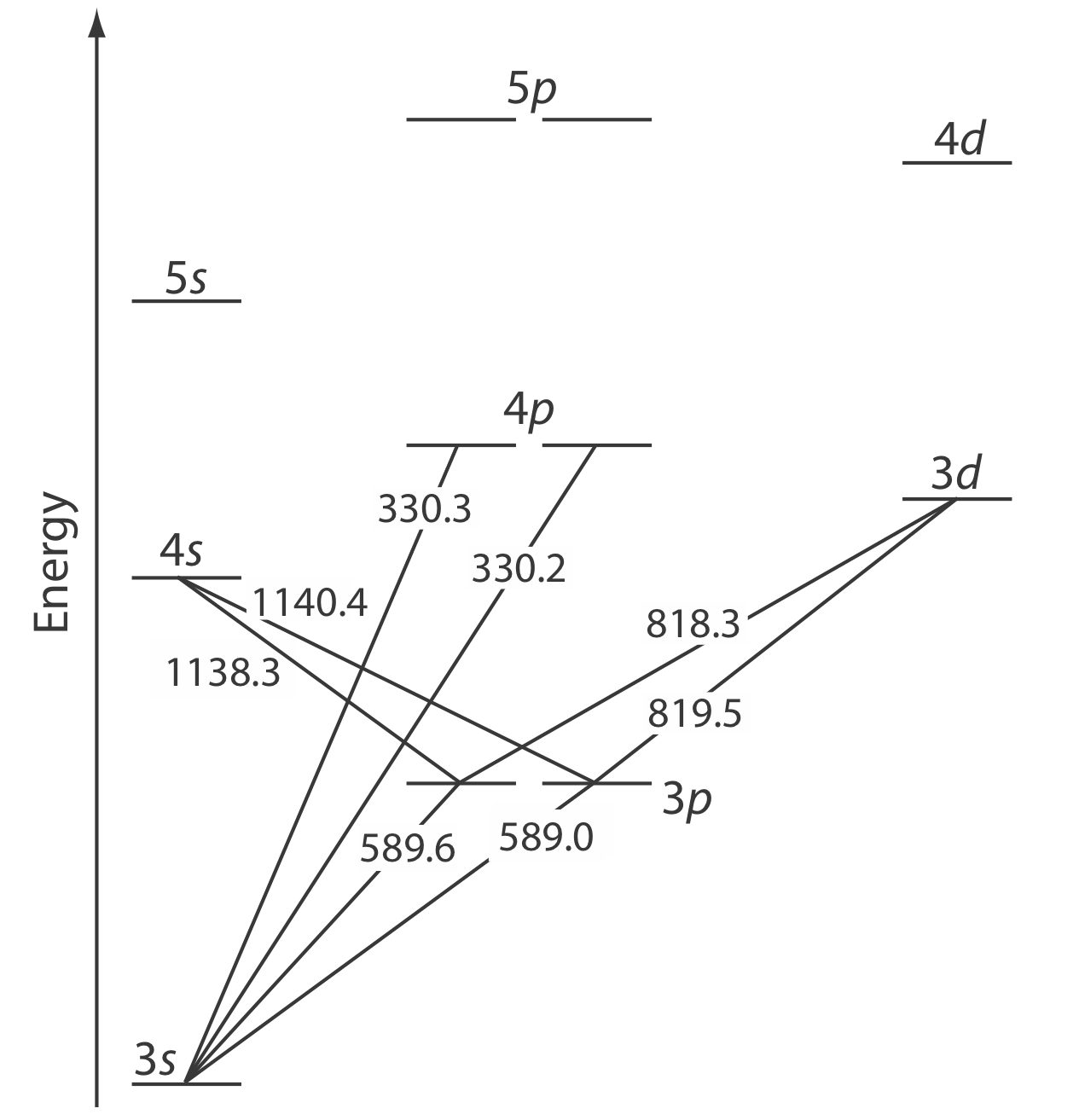
La absorción de un fotón se acompaña de la excitación de un electrón desde un orbital atómico de menor energía a un orbital atómico de mayor energía. No se permiten todas las transiciones posibles entre orbitales atómicos. Para el sodio las únicas transiciones permitidas son aquellas en las que hay un cambio de ±1 en el número cuántico orbital (l); así se permiten transiciones desde\(s \rightarrow p\) orbitales, pero se prohíben las transiciones desde\(s \rightarrow s\) y desde\(s \rightarrow d\) orbitales.

El espectro de absorción atómica para Na se muestra en la Figura 10.2.6 , y es típico del que se encuentra para la mayoría de los átomos. La característica más obvia de este espectro es que consiste en un pequeño número de líneas de absorción discretas que corresponden a transiciones entre el estado fundamental (el orbital atómico de 3 s) y los orbitales atómicos de 3 p y 4 p. La absorción de estados excitados, como la\(3p \rightarrow 4s\) y las\(3p \rightarrow 3d\) transiciones incluidas en la Figura 10.2.5 , son demasiado débiles para detectarlas. Debido a que la vida útil de un estado excitado es corta (un átomo de estado excitado normalmente regresa a un estado de energía más baja en 10 ^{—7 a 10 —8} segundos), es probable que un átomo en el estado salido regrese al estado fundamental antes de que tenga la oportunidad de absorber un fotón.

Figura 10.2.6 . Espectro de absorción atómica para sodio. Tenga en cuenta que la escala en el eje x incluye una interrupción.

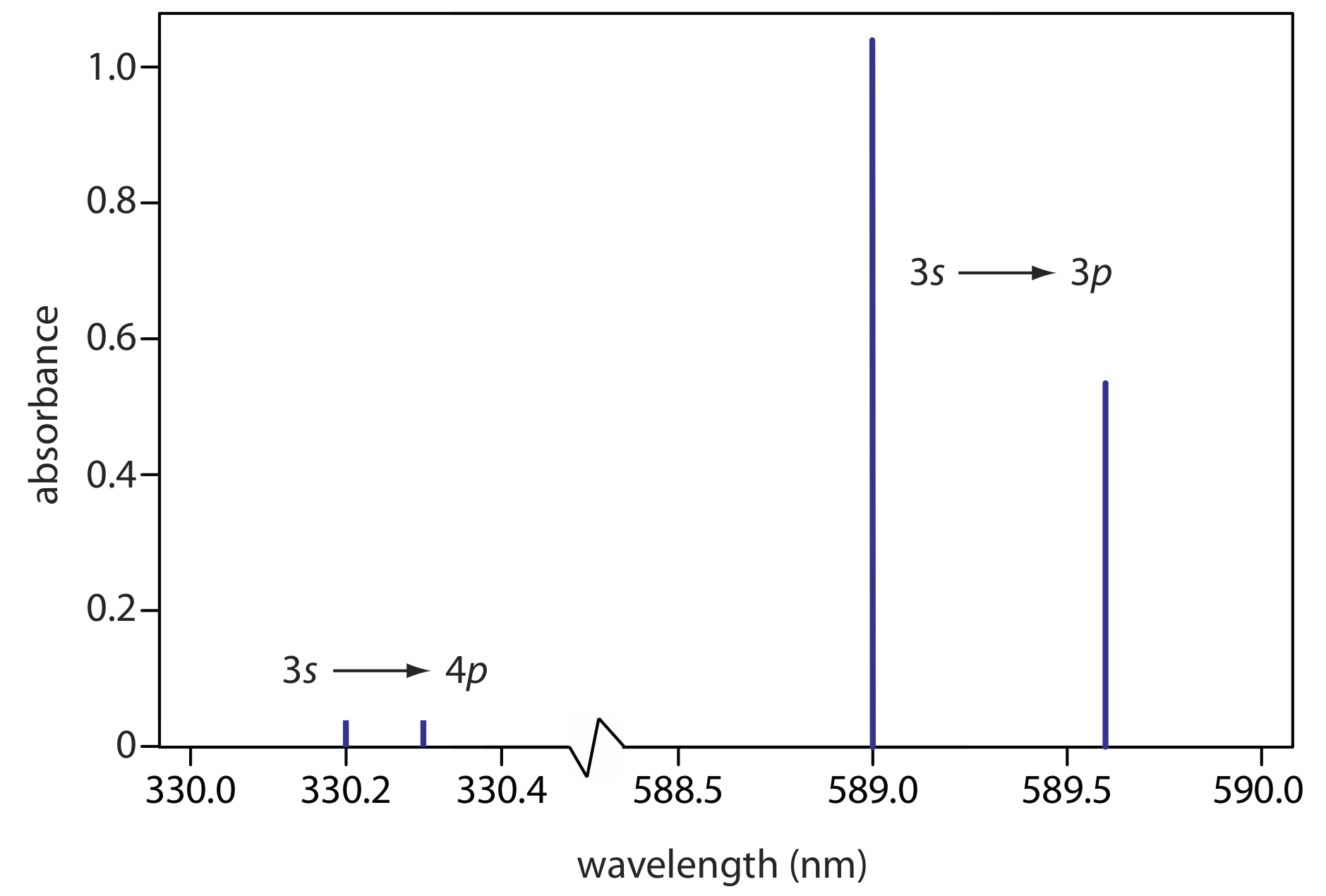
Otra característica del espectro de absorción atómica en la Figura 10.2.6 es el ancho estrecho de las líneas de absorción, que es consecuencia de la diferencia fija de energía entre el estado fundamental y el estado excitado, y la falta de niveles de energía vibratoria y rotacional. Los anchos de línea naturales para la absorción atómica, que se rigen por el principio de incertidumbre, son aproximadamente de 10 ^—5 nm. Otras contribuciones al ensanchamiento incrementan este ancho de línea a aproximadamente 10 ^—3 nm.

Transmitancia y absorbancia

A medida que la luz pasa por una muestra, su poder disminuye a medida que parte de ella es absorbida. Esta atenuación de la radiación se describe cuantitativamente por dos términos separados, pero relacionados: transmitancia y absorbancia. Como se muestra en la Figura 10.2.7 a, la transmitancia es la relación de la potencia de la radiación de la fuente a medida que sale de la muestra, P _T, a ese incidente en la muestra, P ₀.

\[T=\frac{P_{\mathrm{T}}}{P_{0}} \label{10.1}\]

Multiplicar la transmitancia por 100 da el porcentaje de transmitancia,% T, que varía entre 100% (sin absorción) y 0% (absorción completa). Todos los métodos de detección de fotones, incluyendo el ojo humano y los transductores fotoeléctricos modernos, miden la transmitancia de la radiación electromagnética.

Figura 10.2.7 . a) Diagrama esquemático que muestra la atenuación de la radiación que pasa a través de una muestra; P ₀ es la potencia radiante de la fuente y P _T es la potencia radiante transmitida por la muestra. (b) Diagrama esquemático que muestra cómo redefinimos P ₀ como la potencia radiante transmitida por el espacio en blanco. La redefinición de P ₀ de esta manera corrige la transmitancia en (a) para la pérdida de radiación por dispersión, reflexión, absorción por el recipiente de la muestra y absorción por la matriz de la muestra.

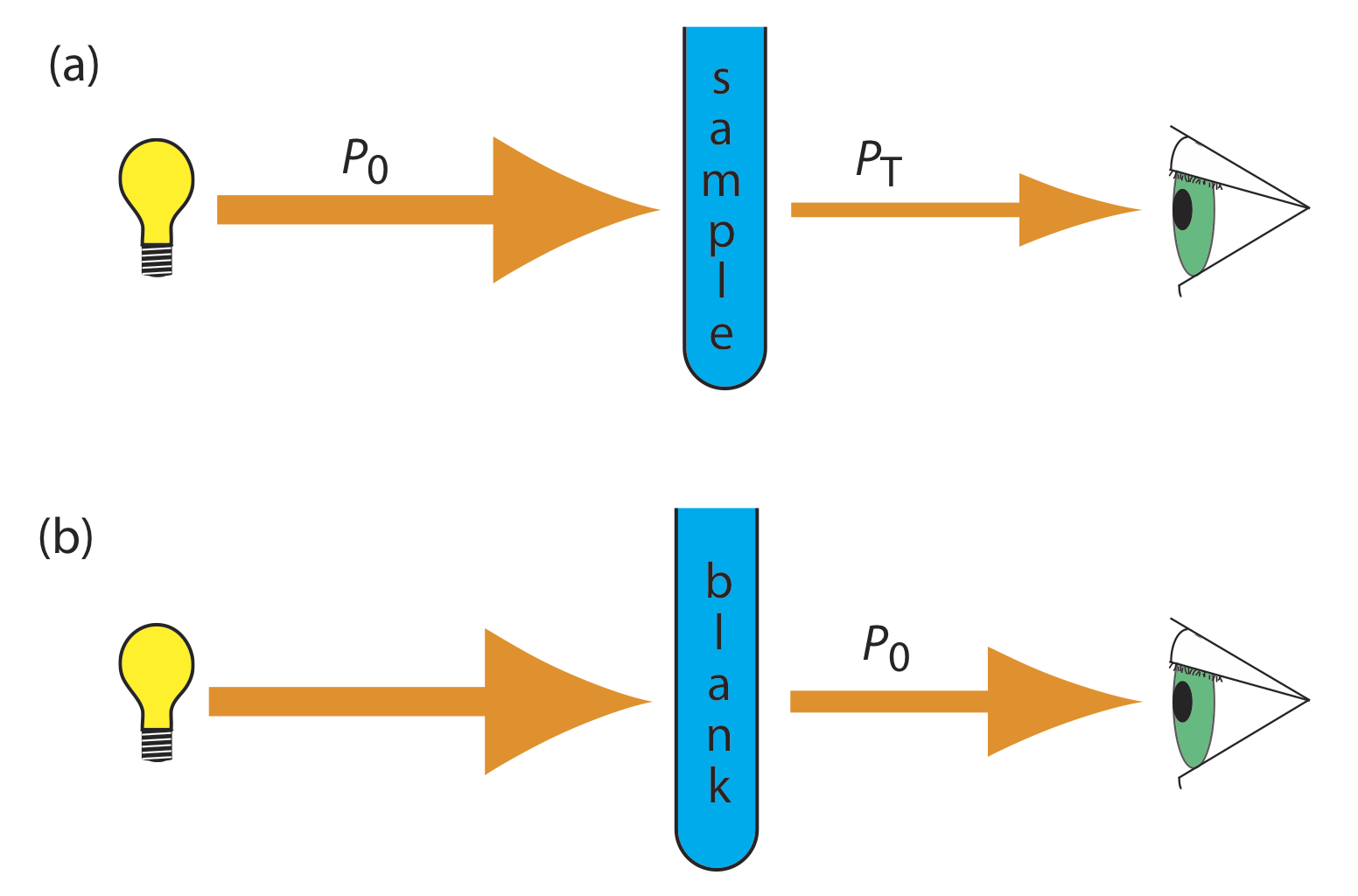
La ecuación\ ref {10.1} no distingue entre diferentes mecanismos que impiden que un fotón emitido por la fuente llegue al detector. Además de la absorción por el analito, varios fenómenos adicionales contribuyen a la atenuación de la radiación, incluyendo la reflexión y absorción por el recipiente de la muestra, la absorción por otros componentes en la matriz de la muestra y la dispersión de la radiación. Para compensar esta pérdida de la potencia de la radiación, utilizamos un método en blanco. Como se muestra en la Figura 10.2.7 b, redefinimos P ₀ como la potencia que sale del método en blanco.

Un método alternativo para expresar la atenuación de la radiación electromagnética es la absorbancia, A, que definimos como

\[A=-\log T=-\log \frac{P_{\mathrm{T}}}{P_{0}} \label{10.2}\]

La absorbancia es la unidad más común para expresar la atenuación de la radiación porque es una función lineal de la concentración del analito.

Demostraremos que esto es cierto en la siguiente sección cuando introduzcamos la ley de Beer.

Ejemplo 10.2.1

Una muestra tiene un porcentaje de transmitancia de 50%. ¿Cuál es su absorbancia?

Solución

Un porcentaje de transmitancia de 50.0% es lo mismo que una transmitancia de 0.500. Sustituyendo en la ecuación\ ref {10.2} da

\[A=-\log T=-\log (0.500)=0.301 \nonumber\]

Ejercicio 10.2.1

¿Cuál es el% T para una muestra si su absorbancia es 1.27?

Contestar

Para encontrar la transmitancia, T, comenzamos por señalar que

\[A=1.27=-\log T \nonumber\]

Resolviendo para T

\[\begin{array}{c}{-1.27=\log T} \\ {10^{-1.27}=T}\end{array} \nonumber\]

da una transmitancia de 0.054, o un %T de 5.4%.

La ecuación\ ref {10.1} tiene una consecuencia importante para la absorción atómica. Como aprendimos de la Figura 10.2.6 , las líneas de absorción atómica son muy estrechas. Incluso con un monocromador de alta calidad, el ancho de banda efectivo para una fuente continua es\(100-1000 \times\) mayor que el ancho de una línea de absorción atómica. Como resultado, se absorbe poca radiación de una fuente continua cuando pasa a través de una muestra de átomos; debido a que P ₀ ≈ P _T la absorbancia medida efectivamente es cero. Por esta razón, la absorción atómica requiere que usemos una fuente lineal en lugar de una fuente continua.

Absorbancia y Concentración: Ley de Cerveza

Cuando la radiación electromagnética monocromática pasa a través de una capa infinitesimalmente delgada de muestra de espesor dx, experimenta una disminución en su potencia de dP (Figura 10.2.8 ).

Figura 10.2.8 . Factores utilizados para derivar la ley de la Cerveza.

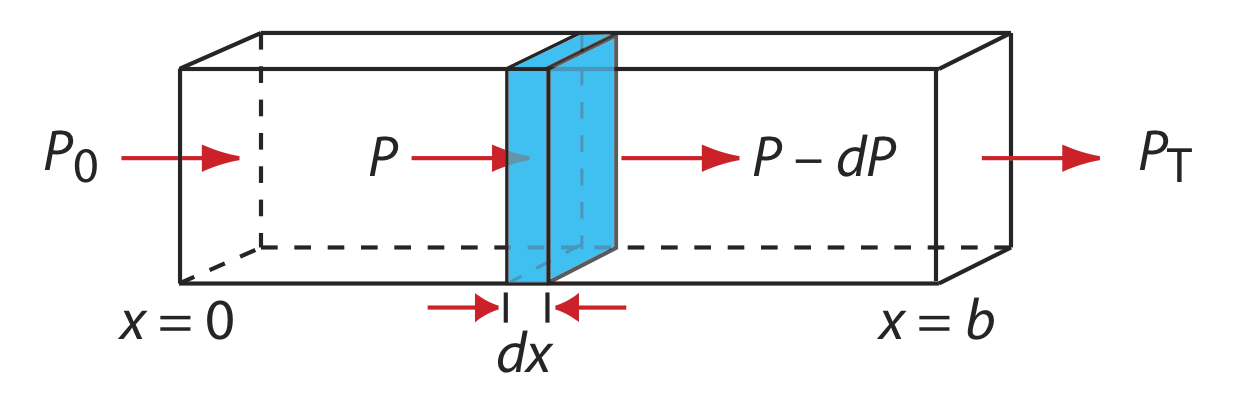
Esta disminución fraccionaria en la potencia es proporcional al grosor de la muestra y a la concentración del analito, C; así

\[-\frac{d P}{P}=\alpha C d x \label{10.3}\]

donde P es la potencia incidente sobre la capa delgada de la muestra y\(\alpha\) es una constante de proporcionalidad. Integrando el lado izquierdo de la ecuación\ ref {10.3} sobre el grosor completo de la muestra

\[-\int_{P=P_0}^{P=P_t} \frac{d P}{P}=\alpha C \int_{x=0}^{x=b} d x \nonumber\]

\[\ln \frac{P_{0}}{P_T}=\alpha b C \nonumber\]

convertir de ln a log, y sustituyendo a la ecuación\ ref {10.2}, da

\[A=a b C \label{10.4}\]

donde a es la absortividad del analito con unidades de cm ^—1 conc ^—1. Si expresamos la concentración usando molaridad, entonces reemplazamos a con la absortividad molar\(\varepsilon\), que tiene unidades de cm ^—1 M ^—1.

\[A=\varepsilon b C \label{10.5}\]

La absortividad y la absortividad molar son proporcionales a la probabilidad de que el analito absorba un fotón de una energía dada. Como resultado, los valores tanto para a como\(\varepsilon\) dependen de la longitud de onda del fotón absorbido.

Ejemplo 10.2.2

Se coloca una solución\(5.00 \times 10^{-4}\) M de analito en una celda de muestra que tiene una longitud de trayectoria de 1.00 cm. A una longitud de onda de 490 nm, la absorbancia de la solución es 0.338. ¿Cuál es la absortividad molar del analito a esta longitud de onda?

Solución

Resolviendo la ecuación\ ref {10.5} para\(\epsilon\) y hacer sustituciones apropiadas da

\[\varepsilon=\frac{A}{b C}=\frac{0.338}{(1.00 \ \mathrm{cm})\left(5.00 \times 10^{-4} \ \mathrm{M}\right)}=676 \ \mathrm{cm}^{-1} \ \mathrm{M}^{-1} \nonumber\]

Ejercicio 10.2.2

Una solución del analito del Ejemplo 10.2.2 tiene una absorbancia de 0.228 en una celda de muestra de 1.00-cm. ¿Cuál es la concentración del analito?

Contestar

Hacer las sustituciones apropiadas en la ley de Beer

\[A=0.228=\varepsilon b C=\left(676 \ \mathrm{M}^{-1} \ \mathrm{cm}^{-1}\right)(1 \ \mathrm{cm}) C \nonumber\]

y resolver para C da una concentración de\(3.37 \times 10^{-4}\) M.

La ecuación\ ref {10.4} y la ecuación\ ref {10.5}, que establecen la relación lineal entre absorbancia y concentración, se conocen como ley de Beer. Las curvas de calibración basadas en la ley de Beer son comunes en los análisis cuantitativos.

Como suele ocurrir, la formulación de una ley es más complicada de lo que su nombre sugiere. Este es el caso, por ejemplo, de la ley de Beer, que también se conoce como la ley Beer-Lambert o la ley Beer-Lambert-Bouguer. Pierre Bouguer, en 1729, y Johann Lambert, en 1760, señalaron que la transmitancia de la luz disminuye exponencialmente con un aumento en el grosor de la muestra.

\[T \propto e^{-b} \nonumber\]

Posteriormente, en 1852, August Beer señaló que la transmitancia de la luz disminuye exponencialmente a medida que aumenta la concentración de las especies absorbentes.

\[T \propto e^{-C} \nonumber\]

Juntos, y cuando se escriben en términos de absorbancia en lugar de transmitancia, estas dos relaciones conforman lo que conocemos como ley de Beer.

Ley de Cerveza y Muestras Multicomponentes

Podemos extender la ley de Beer a una muestra que contenga varios componentes absorbentes. Si no hay interacciones entre los componentes, entonces las absorbancias individuales, A _i, son aditivas. Para una mezcla de dos componentes de X e Y de analitos, la absorbancia total, A _tot, es

\[A_{tot}=A_{X}+A_{Y}=\varepsilon_{X} b C_{X}+\varepsilon_{Y} b C_{Y} \nonumber\]

Generalizando, la absorbancia para una mezcla de n componentes, una _mezcla, es

\[A_{m i x}=\sum_{i=1}^{n} A_{i}=\sum_{i=1}^{n} \varepsilon_{i} b C_{i} \label{10.6}\]

Limitaciones a la Ley de Cerveza

La ley de Beer sugiere que una trama de absorbancia vs. concentración —llamaremos a esto una trama de ley de Beer— es una línea recta con una intersección y de cero y una pendiente de ab o\(\varepsilon b\). En algunos casos una trama de ley de Beer se desvía de este comportamiento ideal (ver Figura 10.2.9 ), y tales desviaciones de la linealidad se dividen en tres categorías: fundamental, química e instrumental.

Figura 10.2.9 . Gráficas de absorbancia vs concentración que muestran desviaciones positivas y negativas de la relación ideal de la ley de Beer, que es una línea recta.

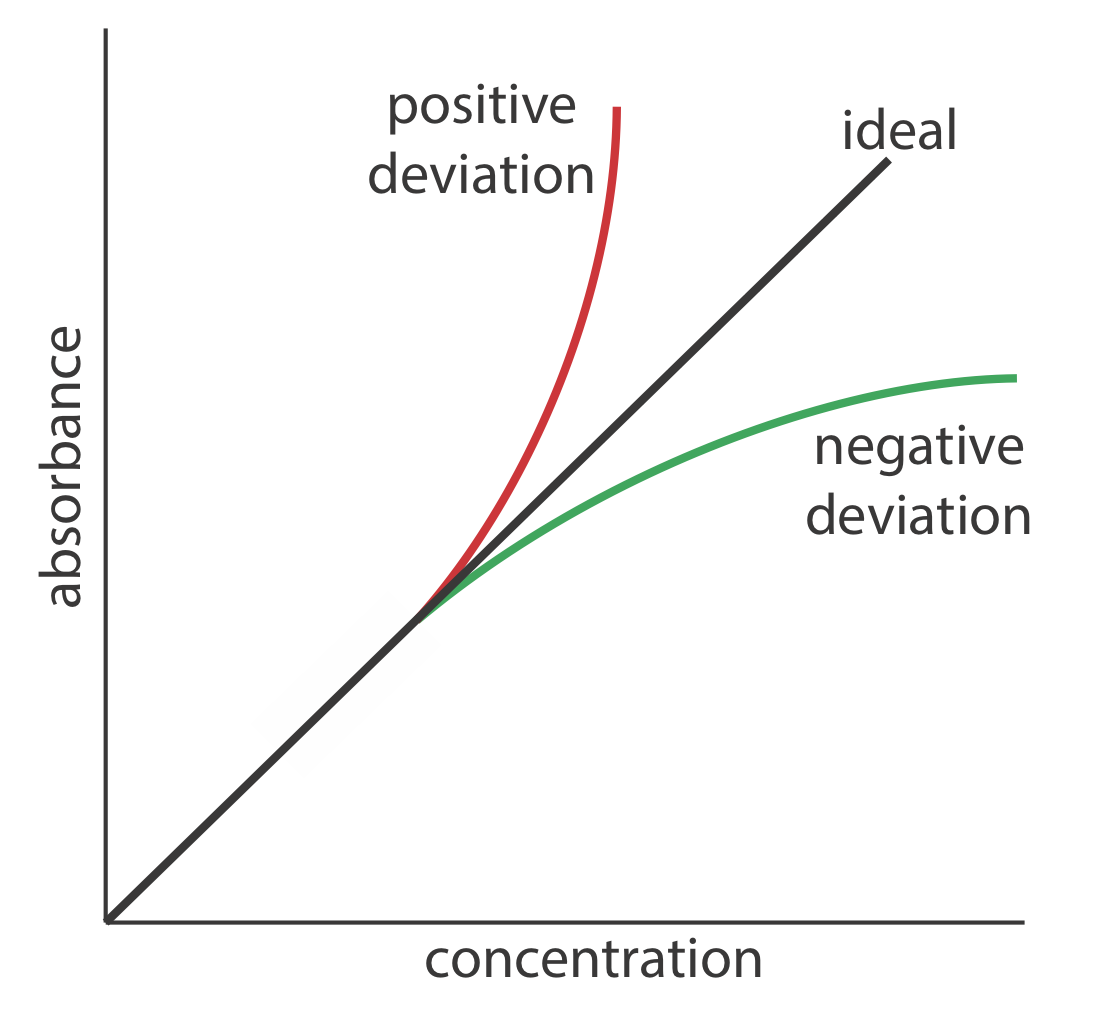
Limitaciones fundamentales a la Ley de Cerveza

La ley de la cerveza es una ley limitante que solo es válida para bajas concentraciones de analito. Hay dos aportes a esta limitación fundamental a la ley de Beer. A concentraciones más altas las partículas individuales de analito ya no son independientes entre sí. La interacción resultante entre partículas de analito puede cambiar la capacidad de absorción del analito. Una segunda contribución es que la absortividad de un analito depende del índice de refracción de la solución. Debido a que el índice de refracción de una solución varía con la concentración del analito, los valores de a y\(\varepsilon\) pueden cambiar. Para concentraciones suficientemente bajas de analito, el índice de refracción es esencialmente constante y una gráfica de la ley de Beer es lineal.

Limitaciones Químicas a la Ley de Cerveza

Una desviación química de la ley de Beer puede ocurrir si el analito está involucrado en una reacción de equilibrio. Consideremos, por ejemplo, el ácido débil, el HA. Para construir una parcela de ley de Beer, preparamos una serie de soluciones estándar, cada una de las cuales contiene una concentración total conocida de HA, y luego medimos la absorbancia de cada solución a la misma longitud de onda. Debido a que el HA es un ácido débil, está en equilibrio con su base débil conjugada, A ^—.

En las ecuaciones que siguen, la base débil conjugada A ^— se escribe como A ya que es fácil confundir el símbolo con carga aniónica como un signo menos.

\[\mathrm{HA}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{A}^{-}(a q) \nonumber\]

^{Si tanto HA como A absorben a la longitud de onda seleccionada, entonces la ley de Beer es}

\[A=\varepsilon_{\mathrm{HA}} b C_{\mathrm{HA}}+\varepsilon_{\mathrm{A}} b C_{\mathrm{A}} \label{10.7}\]

Porque la concentración total del ácido débil, C _total, es

\[C_{\mathrm{total}}=C_{\mathrm{HA}}+C_{\mathrm{A}} \nonumber\]

podemos escribir las concentraciones de HA y A ^— como

\[C_{\mathrm{HA}}=\alpha_{\mathrm{HA}} C_{\mathrm{total}} \label{10.8}\]

\[C_{\text{A}} = (1 - \alpha_\text{HA})C_\text{total} \label{10.9}\]

donde\(\alpha_\text{HA}\) está la fracción de ácido débil presente como HA. Sustituyendo la ecuación\ ref {10.8} y la ecuación\ ref {10.9} en la ecuación\ ref {10.7} y reordenando, da

\[A=\left(\varepsilon_{\mathrm{HA}} \alpha_{\mathrm{HA}}+\varepsilon_{\mathrm{A}}-\varepsilon_{\mathrm{A}} \alpha_{\mathrm{A}}\right) b C_{\mathrm{total}} \label{10.10}\]

Para obtener una parcela lineal de ley de Beer, debemos cumplir una de dos condiciones. Si\(\varepsilon_\text{HA}\) y\(\varepsilon_{\text{A}}\) tienen el mismo valor en la longitud de onda seleccionada, entonces la Ecuación\ ref {10.10} simplifica a

\[A = \varepsilon_{\text{A}}bC_\text{total} = \varepsilon_\text{HA}bC_\text{total} \nonumber\]

Alternativamente, si\(\alpha_\text{HA}\) tiene el mismo valor para todas las soluciones estándar, entonces cada término dentro de los paréntesis de la Ecuación\ ref {10.10} es constante, que reemplazamos con k, y se obtiene una curva de calibración lineal en cualquier longitud de onda.

\[A=k b C_{\mathrm{total}} \nonumber\]

Debido a que el HA es un ácido débil, el valor de\(\alpha_\text{HA}\) varía con el pH. Para mantener\(\alpha_\text{HA}\) constante, amortiguamos cada solución estándar al mismo pH. Dependiendo de los valores relativos de\(\alpha_\text{HA}\) y\(\alpha_{\text{A}}\), la curva de calibración tiene una desviación positiva o negativa de la ley de Beer si no amortiguamos los estándares al mismo pH.

Limitaciones instrumentales a la ley de la cerveza

Hay dos limitaciones instrumentales principales a la ley de Beer. La primera limitación es que la ley de Beer asume que la radiación que llega a la muestra es de una sola longitud de onda, es decir, asume una fuente de radiación puramente monocromática. Como se muestra en la Figura 10.1.10, incluso el mejor selector de longitud de onda pasa la radiación con un ancho de banda efectivo pequeño pero finito. La radiación policromática siempre da una desviación negativa de la ley de Beer, pero el efecto es menor si el valor de\(\varepsilon\) esencialmente es constante sobre el rango de longitud de onda pasado por el selector de longitud de onda. Por esta razón, como se muestra en la Figura 10.2.10 , es mejor realizar mediciones de absorbancia en la parte superior de un pico de absorción amplio. Además, la desviación de la ley de Beer es menos grave si el ancho de banda efectivo de la fuente es inferior a una décima parte del ancho de banda natural de la especie absorbente [(a) Strong, F. C., III Anal. Chem. 1984, 56, 16A—34A; Gilbert, D. D. J. Chem. Educ. 1991, 68, A278—A281]. Cuando se deben realizar mediciones en una pendiente, se mejora la linealidad mediante el uso de un ancho de banda efectivo más estrecho.

Figura 10.2.10 . Efecto de la selección de longitud de onda sobre la linealidad de una parcela de ley de Beer. Otra razón para medir la absorbancia en la parte superior de un pico de absorbancia es que proporciona un análisis más sensible. Tenga en cuenta que la trama de la ley de la cerveza verde tiene una pendiente más pronunciada y, por lo tanto, una mayor sensibilidad, que la trama de la ley de la cerveza roja. Una parcela de ley de Beer, por supuesto, equivale a una curva de calibración.

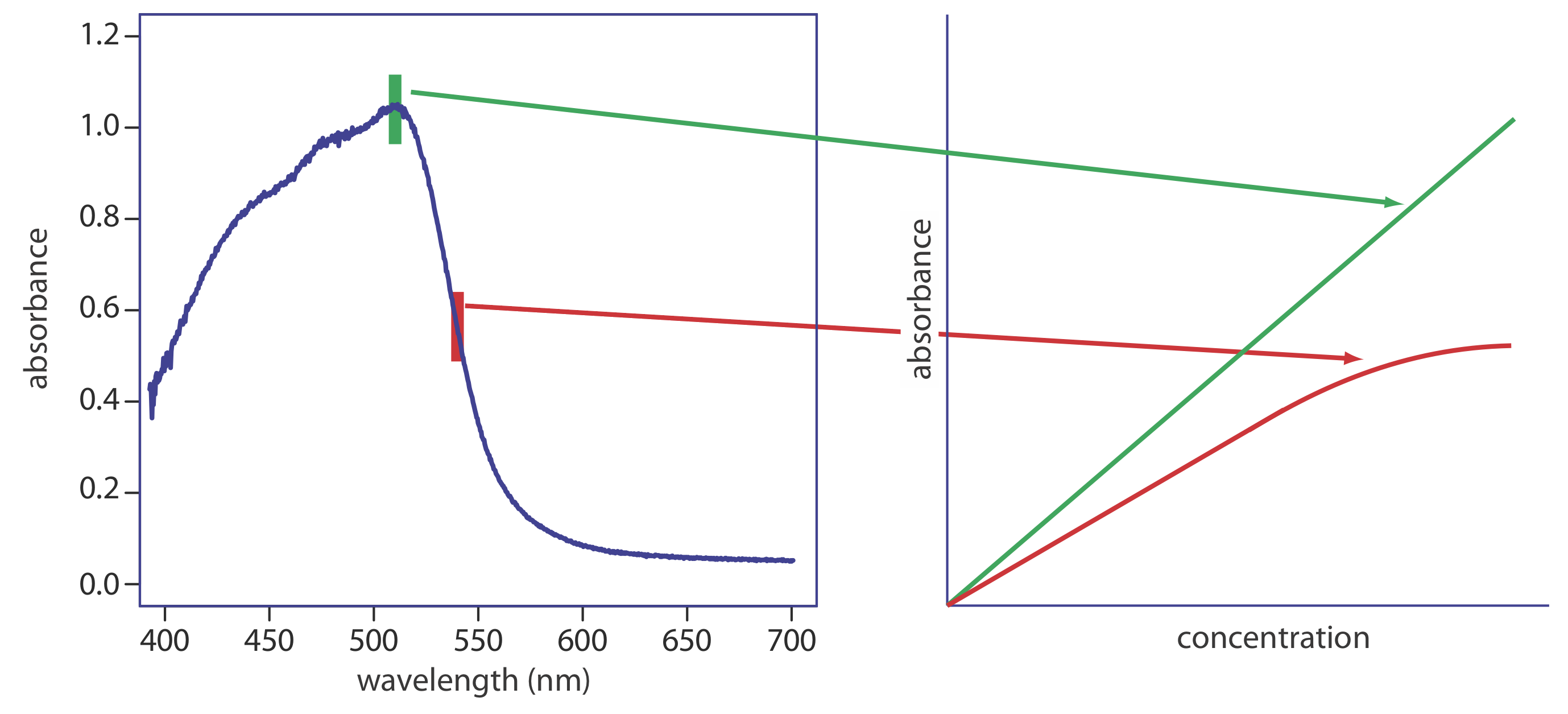
La radiación parásita es la segunda contribución a las desviaciones instrumentales de la ley de Beer. La radiación parásita surge de imperfecciones en el selector de longitud de onda que permiten que la luz ingrese al instrumento y llegue al detector sin pasar por la muestra. La radiación parásita agrega una contribución adicional, P _parásita, a la potencia radiante que llega al detector; así

\[A=-\log \frac{P_{\mathrm{T}}+P_{\text { stray }}}{P_{0}+P_{\text { stray }}} \nonumber\]

Para una pequeña concentración de analito, P _parásito es significativamente menor que P ₀ y P _T, y la absorbancia no se ve afectada por la radiación parásita. Para mayores concentraciones de analito, menos luz pasa a través de la muestra y P _T y P _se vuelven similares en magnitud. Este resultado es una absorbancia menor de lo esperado, y una desviación negativa de la ley de Beer.