10.1: Visión general de la espectroscopia
- Page ID
- 75913
El enfoque de este capítulo está en la interacción de la radiación ultravioleta, visible e infrarroja con la materia. Debido a que estas técnicas utilizan materiales ópticos para dispersar y enfocar la radiación, a menudo se identifican como espectroscopias ópticas. Para mayor comodidad utilizaremos el término espectroscopia más simple en lugar de espectroscopia óptica; sin embargo, debe entender que consideraremos solo una parte limitada de lo que es un área mucho más amplia de técnicas analíticas.
A pesar de la diferencia en la instrumentación, todas las técnicas espectroscópicas comparten varias características comunes. Antes de considerar ejemplos individuales con mayor detalle, tomemos un momento para considerar algunas de estas similitudes. A medida que trabajas en el capítulo, este resumen te ayudará a enfocarte en las similitudes entre los diferentes métodos espectroscópicos de análisis. Te resultará más fácil entender un nuevo método analítico cuando puedas ver su relación con otros métodos similares.
¿Qué es la Radiación Electromagnética?
La radiación electromagnética —luz— es una forma de energía cuyo comportamiento se describe por las propiedades tanto de las ondas como de las partículas. Algunas propiedades de la radiación electromagnética, como su refracción cuando pasa de un medio a otro (Figura 10.1.1 ), se explican mejor cuando describimos la luz como una onda. Otras propiedades, como la absorción y emisión, se describen mejor al tratar la luz como una partícula. La naturaleza exacta de la radiación electromagnética sigue sin estar clara, como lo ha hecho desde el desarrollo de la mecánica cuántica en el primer cuarto del siglo XX [Home, D.; Gribbin, J. New Scientist 1991, 2 Nov. 30—33]. Sin embargo, este modelo dual de comportamiento de onda y partícula proporciona una descripción útil para la radiación electromagnética.
Propiedades de onda de la radiación electromagnética
La radiación electromagnética consiste en campos eléctricos y magnéticos oscilantes que se propagan a través del espacio a lo largo de una trayectoria lineal y con una velocidad constante. En un vacío, la radiación electromagnética viaja a la velocidad de la luz, c, que es\(2.99792 \times 10^8\) m/s. cuando la radiación electromagnética se mueve a través de un medio que no sea vacío, su velocidad, v, es menor que la velocidad de la luz en un vacío. La diferencia entre v y c es suficientemente pequeña (< 0.1%) para que la velocidad de la luz a tres cifras significativas,\(3.00 \times 10^8\) m/s, sea lo suficientemente precisa para la mayoría de los propósitos.
Las oscilaciones en el campo eléctrico y el campo magnético son perpendiculares entre sí y a la dirección de propagación de la onda. La Figura 10.1.2 muestra un ejemplo de radiación electromagnética polarizada en el plano, que consiste en un solo campo eléctrico oscilante y un solo campo magnético oscilante.
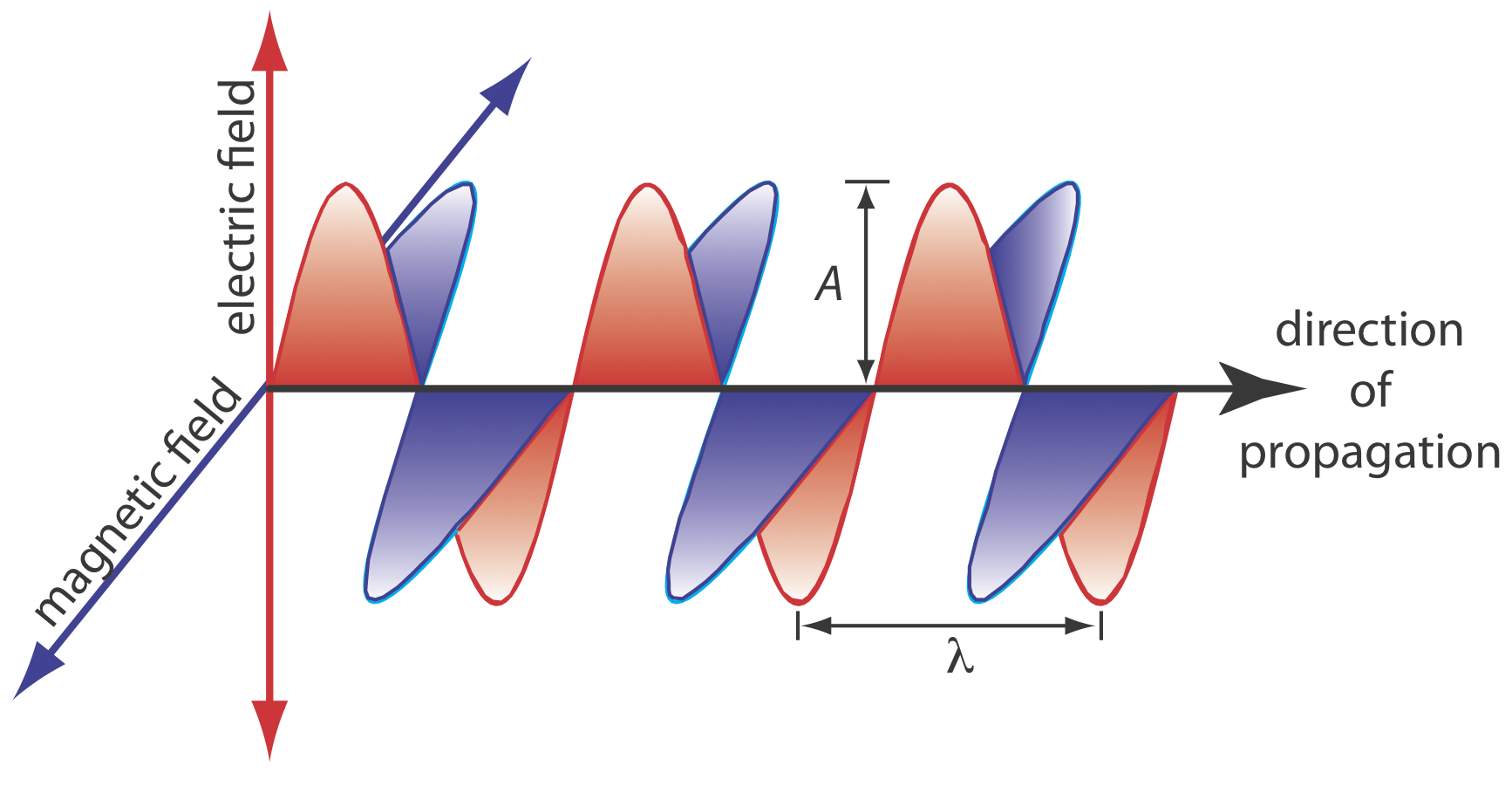
Una onda electromagnética se caracteriza por varias propiedades fundamentales, incluyendo su velocidad, amplitud, frecuencia, ángulo de fase, polarización y dirección de propagación [Ball, D. W. Spectroscopy 1994, 9 (5), 24—25]. Por ejemplo, la amplitud del campo eléctrico oscilante en cualquier punto a lo largo de la onda de propagación es
\[A_{t}=A_{e} \sin (2 \pi \nu t+\Phi) \nonumber\]
donde A t es la magnitud del campo eléctrico en el tiempo t, A e es la amplitud máxima del campo eléctrico,\(\nu\) es la frecuencia de la onda —el número de oscilaciones en el campo eléctrico por unidad de tiempo, y\(\Phi\) es un ángulo de fase que explica el hecho de que A t no necesita tener un valor de cero a t = 0. La ecuación idéntica para el campo magnético es
\[A_{t}=A_{m} \sin (2 \pi \nu t+\Phi) \nonumber\]
donde A m es la amplitud máxima del campo magnético.
Otras propiedades también son útiles para caracterizar el comportamiento de onda de la radiación electromagnética. La longitud de onda\(\lambda\),, se define como la distancia entre máximos sucesivos (ver Figura 10.1.2 ). Para la radiación electromagnética ultravioleta y visible la longitud de onda generalmente se expresa en nanómetros (1 nm = 10 —9 m), y para la radiación infrarroja se expresa en micras (1 mm = 10 —6 m). La relación entre longitud de onda y frecuencia es
\[\lambda = \frac {c} {\nu} \nonumber\]
Otra unidad útil de la unidad es el número de onda\(\overline{\nu}\), que es el recíproco de la longitud de onda
\[\overline{\nu} = \frac {1} {\lambda} \nonumber\]
Los números de onda se utilizan frecuentemente para caracterizar la radiación infrarroja, con las unidades dadas en cm —1.
Cuando la radiación electromagnética se mueve entre diferentes medios, por ejemplo, cuando se mueve del aire al agua\(\nu\), su frecuencia permanece constante. Debido a que su velocidad depende del medio en el que viaja, la longitud de onda de la radiación electromagnética,\(\lambda\), cambia. Si reemplazamos la velocidad de la luz en un vacío, c, con su velocidad en el medio\(v\), entonces la longitud de onda es
\[\lambda = \frac {v} {\nu} \nonumber\]
Este cambio en la longitud de onda a medida que la luz pasa entre dos medios explica la refracción de la radiación electromagnética mostrada en la Figura 10.1.1 .
En 1817, Josef Fraunhofer estudió el espectro de la radiación solar, observando un espectro continuo con numerosas líneas oscuras. Fraunhofer etiquetó con letras la más prominente de las líneas oscuras. En 1859, Gustav Kirchhoff demostró que la línea D en el espectro del sol se debía a la absorción de la radiación solar por los átomos de sodio. La longitud de onda de la línea D de sodio es 589 nm. ¿Cuáles son la frecuencia y el número de onda para esta línea?
Solución
La frecuencia y el número de onda de la línea D de sodio son
\[\nu=\frac{c}{\lambda}=\frac{3.00 \times 10^{8} \ \mathrm{m} / \mathrm{s}}{589 \times 10^{-9} \ \mathrm{m}}=5.09 \times 10^{14} \ \mathrm{s}^{-1} \nonumber\]
\[\overline{\nu}=\frac{1}{\lambda}=\frac{1}{589 \times 10^{-9} \ \mathrm{m}} \times \frac{1 \ \mathrm{m}}{100 \ \mathrm{cm}}=1.70 \times 10^{4} \ \mathrm{cm}^{-1} \nonumber\]
Otra serie históricamente importante de líneas espectrales es la serie Balmer de líneas de emisión a partir de hidrógeno. Una de sus líneas tiene una longitud de onda de 656.3 nm. ¿Cuáles son la frecuencia y el número de onda para esta línea?
- Contestar
-
La frecuencia y el número de onda de la línea son
\[\nu=\frac{c}{\lambda}=\frac{3.00 \times 10^{8} \ \mathrm{m} / \mathrm{s}}{656.3 \times 10^{-9} \ \mathrm{m}}=4.57 \times 10^{14} \ \mathrm{s}^{-1} \nonumber\]
\[\overline{\nu}=\frac{1}{\lambda}=\frac{1}{656.3 \times 10^{-9} \ \mathrm{m}} \times \frac{1 \ \mathrm{m}}{100 \ \mathrm{cm}}=1.524 \times 10^{4} \ \mathrm{cm}^{-1} \nonumber\]
Propiedades de las partículas de la radiación electromagnética
Cuando la materia absorbe radiación electromagnética sufre un cambio de energía. La interacción entre la materia y la radiación electromagnética es más fácil de entender si asumimos que la radiación consiste en un haz de partículas energéticas llamadas fotones. Cuando un fotón es absorbido por una muestra es “destruido” y su energía adquirida por la muestra [Ball, D. W. Spectroscopy 1994, 9 (6) 20—21]. La energía de un fotón, en julios, está relacionada con su frecuencia, longitud de onda y número de onda por las siguientes igualaciones
\[E=h \nu=\frac{h c}{\lambda}=h c \overline{\nu} \nonumber\]
donde h es la constante de Planck, que tiene un valor de\(6.626 \times 10^{-34}\) Js.
¿Cuál es la energía de un fotón de la línea D de sodio a 589 nm?
Solución
La energía del fotón es
\[E=\frac{h c}{\lambda}=\frac{\left(6.626 \times 10^{-34} \ \mathrm{Js}\right)\left(3.00 \times 10^{8} \ \mathrm{m} / \mathrm{s}\right)}{589 \times 10^{-7} \ \mathrm{m}}=3.37 \times 10^{-19} \ \mathrm{J} \nonumber\]
¿Cuál es la energía de un fotón para la línea Balmer a una longitud de onda de 656.3 nm?
- Contestar
-
La energía del fotón es
\[E=\frac{h c}{\lambda}=\frac{\left(6.626 \times 10^{-34} \ \mathrm{Js}\right)\left(3.00 \times 10^{8} \ \mathrm{m} / \mathrm{s}\right)}{656.3 \times 10^{-9} \ \mathrm{m}}=3.03 \times 10^{-19} \ \mathrm{J} \nonumber\]
El espectro electromagnético
La frecuencia y la longitud de onda de la radiación electromagnética varían en muchos órdenes de magnitud. Por conveniencia, dividimos la radiación electromagnética en diferentes regiones, el espectro electromagnético, en función del tipo de transiciones atómicas o moleculares que dan lugar a la absorción o emisión de fotones (Figura 10.1.3 ). Los límites entre las regiones del espectro electromagnético no son rígidos y es posible la superposición entre regiones espectrales.
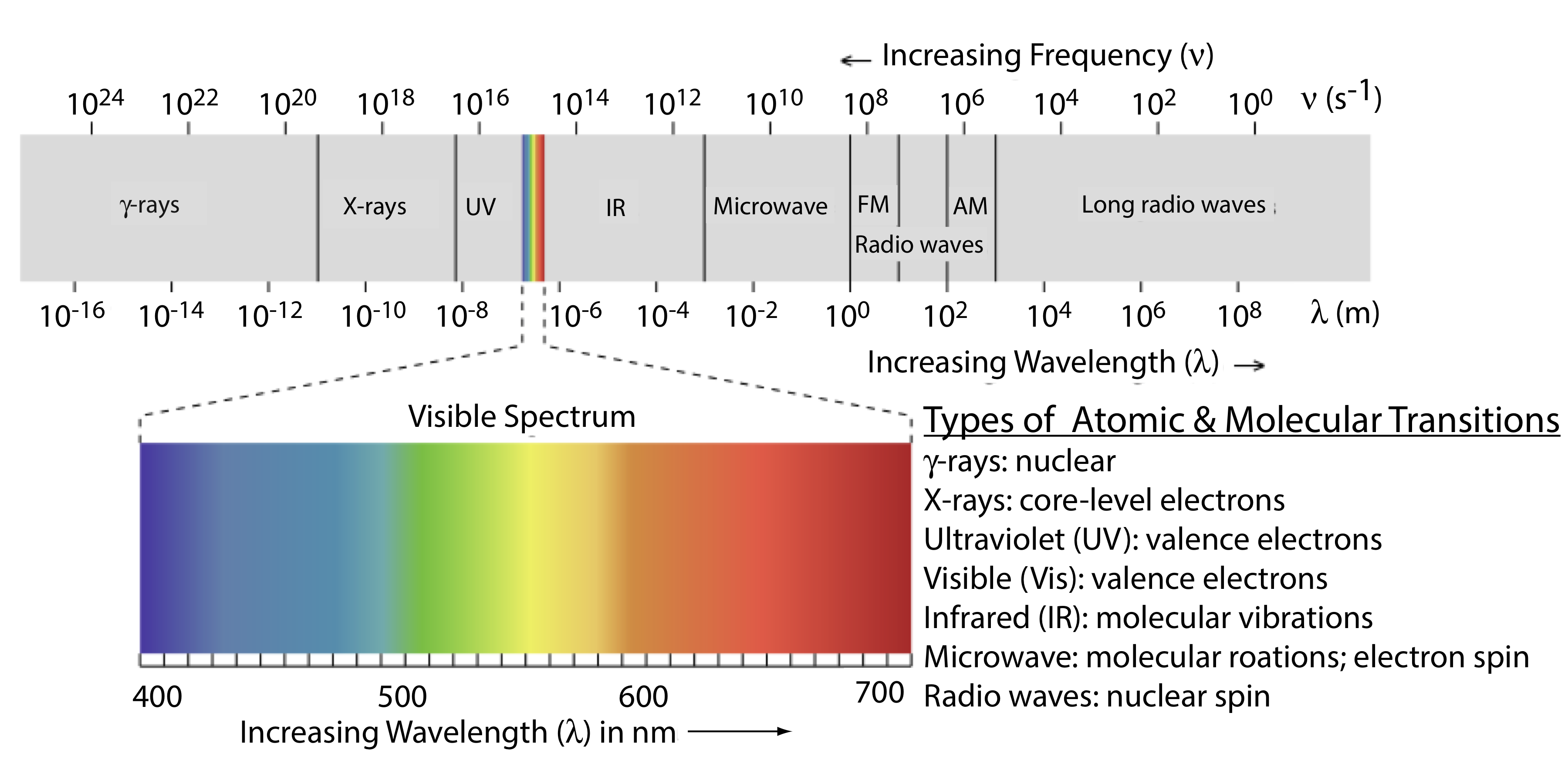
Los fotones como fuente de señal
En la sección anterior definimos varias propiedades características de la radiación electromagnética, incluyendo su energía, velocidad, amplitud, frecuencia, ángulo de fase, polarización y dirección de propagación. Una medición espectroscópica solo es posible si la interacción del fotón con la muestra conduce a un cambio en una o más de estas propiedades características.
Dividiremos la espectroscopia en dos amplias clases de técnicas. En una clase de técnicas hay una transferencia de energía entre el fotón y la muestra. Table 10.1.1 proporciona una lista de varios ejemplos representativos.
En la espectroscopia de absorción un fotón es absorbido por un átomo o molécula, que experimenta una transición de un estado de menor energía a un estado de mayor energía, o estado excitado (Figura 10.1.4 ). El tipo de transición depende de la energía del fotón. El espectro electromagnético en la Figura 10.1.3 , por ejemplo, muestra que la absorción de un fotón de luz visible promueve uno de los electrones de valencia del átomo o molécula a un nivel de energía más alto. Cuando una molécula absorbe radiación infrarroja, por otro lado, uno de sus enlaces químicos experimenta un cambio en la energía vibratoria.
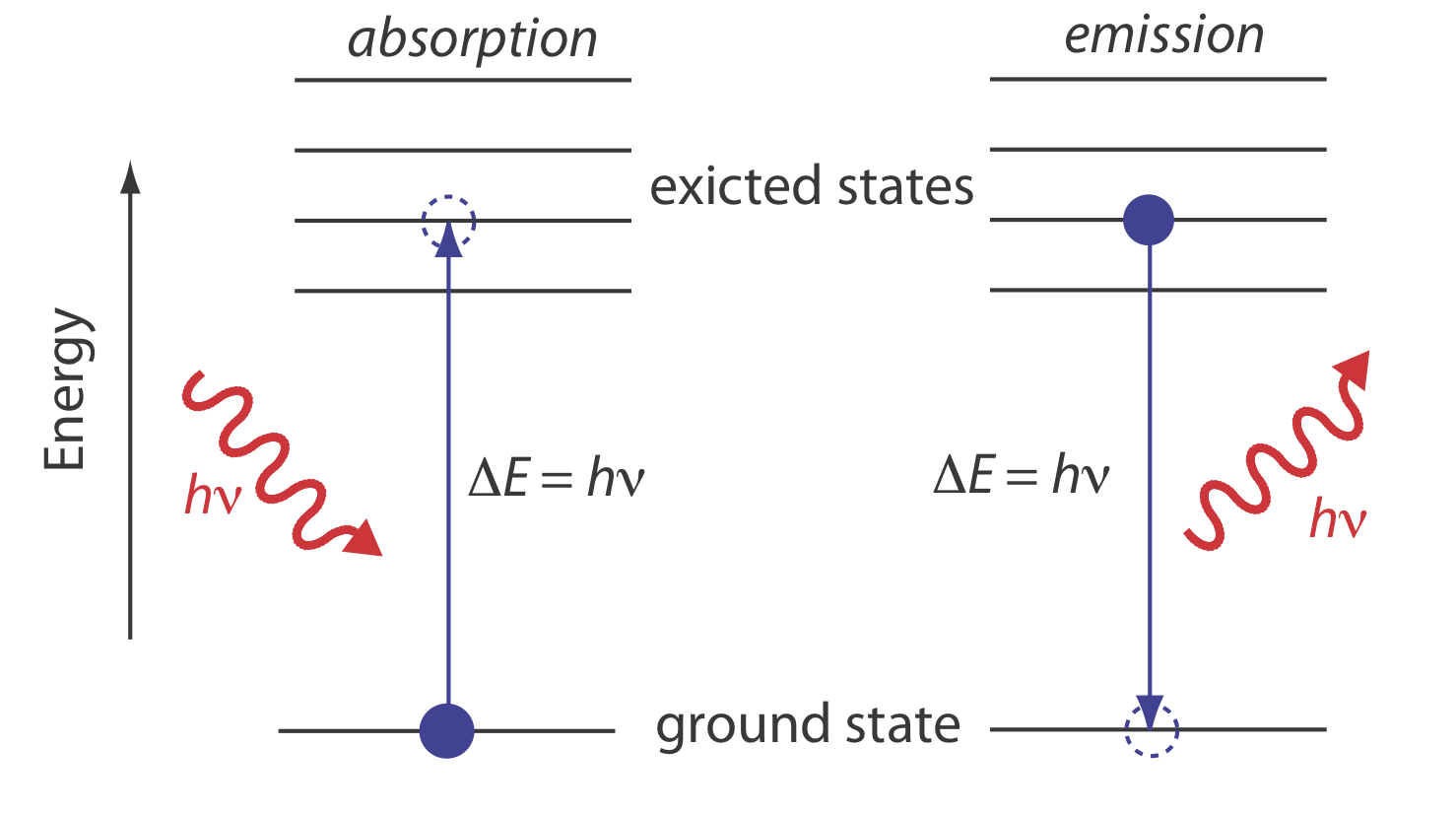
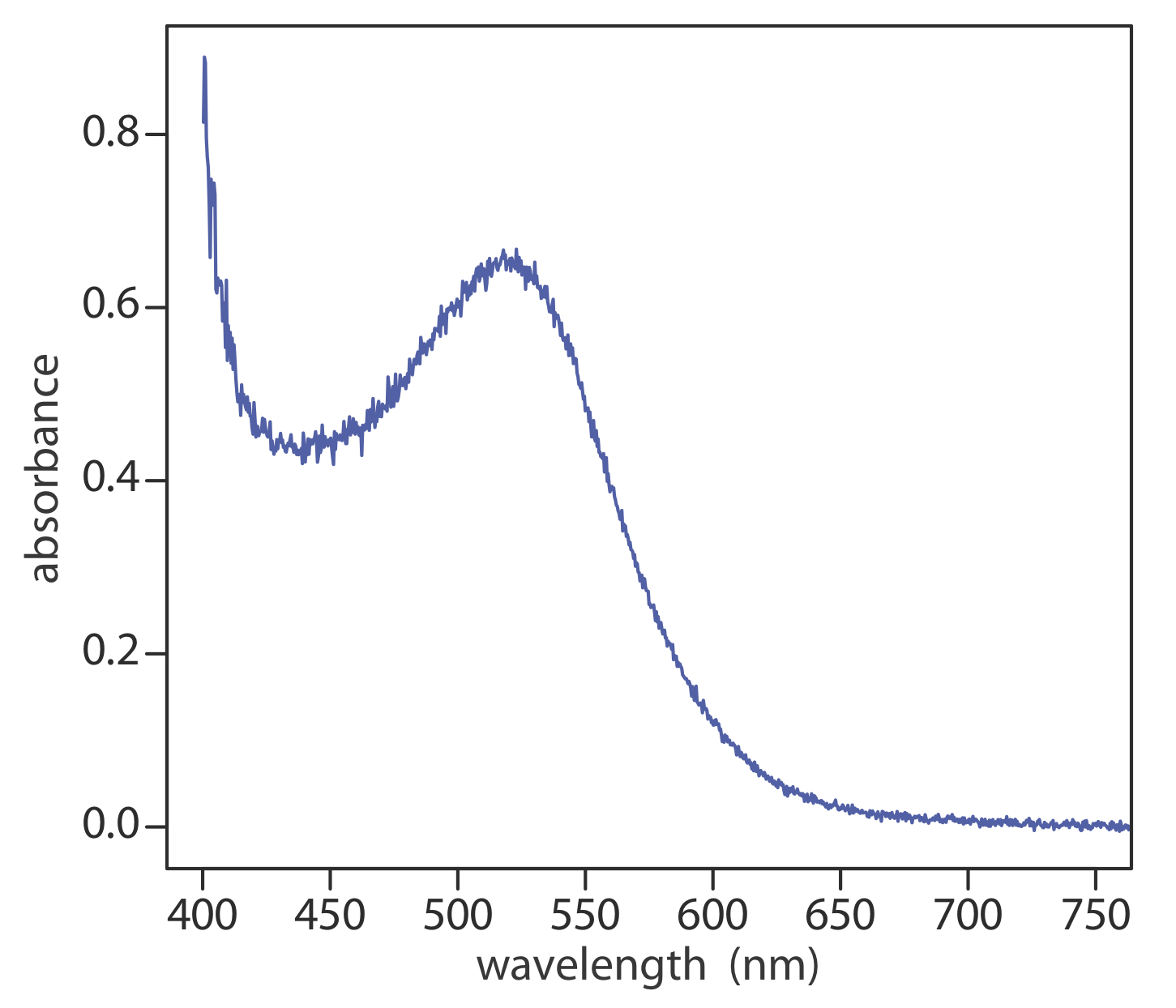
Cuando absorbe radiación electromagnética disminuye el número de fotones que pasan a través de una muestra. La medición de esta disminución de fotones, que llamamos absorbancia, es una señal analítica útil. Tenga en cuenta que cada nivel de energía en la Figura 10.1.4 tiene un valor bien definido porque cada uno está cuantificado. La absorción se produce sólo cuando la energía del fotón,\(h \nu\), coincide con la diferencia de energía,\(\Delta E\), entre dos niveles de energía. Una gráfica de absorbancia en función de la energía del fotón se denomina espectro de absorbancia. La figura 10.1.5 , por ejemplo, muestra el espectro de absorbancia del jugo de arándano.
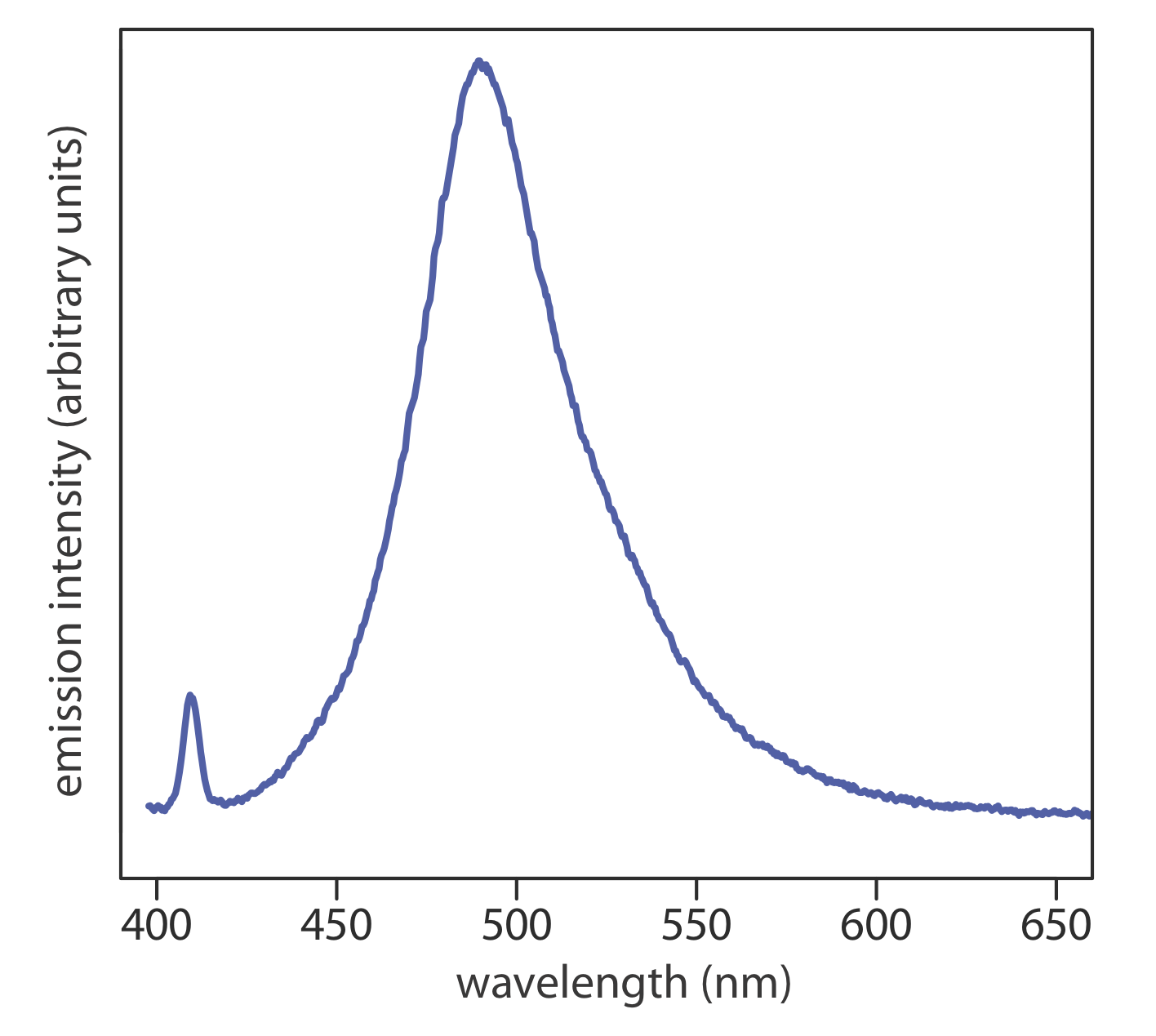
Cuando un átomo o molécula en estado excitado vuelve a un estado de energía más baja, el exceso de energía a menudo se libera como un fotón, un proceso que llamamos emisión (Figura 10.1.4 ). Hay varias formas en las que un átomo o una molécula puede terminar en un estado excitado, incluyendo energía térmica, absorción de un fotón, o como resultado de una reacción química. La emisión después de la absorción de un fotón también se llama fotoluminiscencia, y la que después de una reacción química se llama quimioluminiscencia. Un espectro de emisión típico se muestra en la Figura 10.1.6 .
Las moléculas también pueden liberar energía en forma de calor. Volveremos a este punto más adelante en el capítulo.
En la segunda clase amplia de técnicas espectroscópicas, la radiación electromagnética sufre un cambio de amplitud, ángulo de fase, polarización o dirección de propagación como resultado de su refracción, reflexión, dispersión, difracción o dispersión por la muestra. Varias técnicas espectroscópicas representativas se listan en la Tabla 10.1.2 .
Componentes básicos de instrumentos espectroscópicos
Las técnicas espectroscópicas de la Tabla 10.1.1 y la Tabla 10.1.2 utilizan instrumentos que comparten varios componentes básicos comunes, incluyendo una fuente de energía, un medio para aislar un rango estrecho de longitudes de onda, un detector para medir la señal y un procesador de señal que muestra la señal en una forma conveniente para el analista. En esta sección introducimos estos componentes básicos. Los diseños de instrumentos específicos se consideran en secciones posteriores.
Encontrará un tratamiento más detallado de estos componentes en los recursos adicionales para este capítulo.
Fuentes de Energía
Todas las formas de espectroscopia requieren una fuente de energía. En espectroscopía de absorción y dispersión esta energía es suministrada por fotones. La espectroscopia de emisión y fotoluminiscencia utiliza energía térmica, radiante (fotón) o química para promover el analito a un estado excitado adecuado.
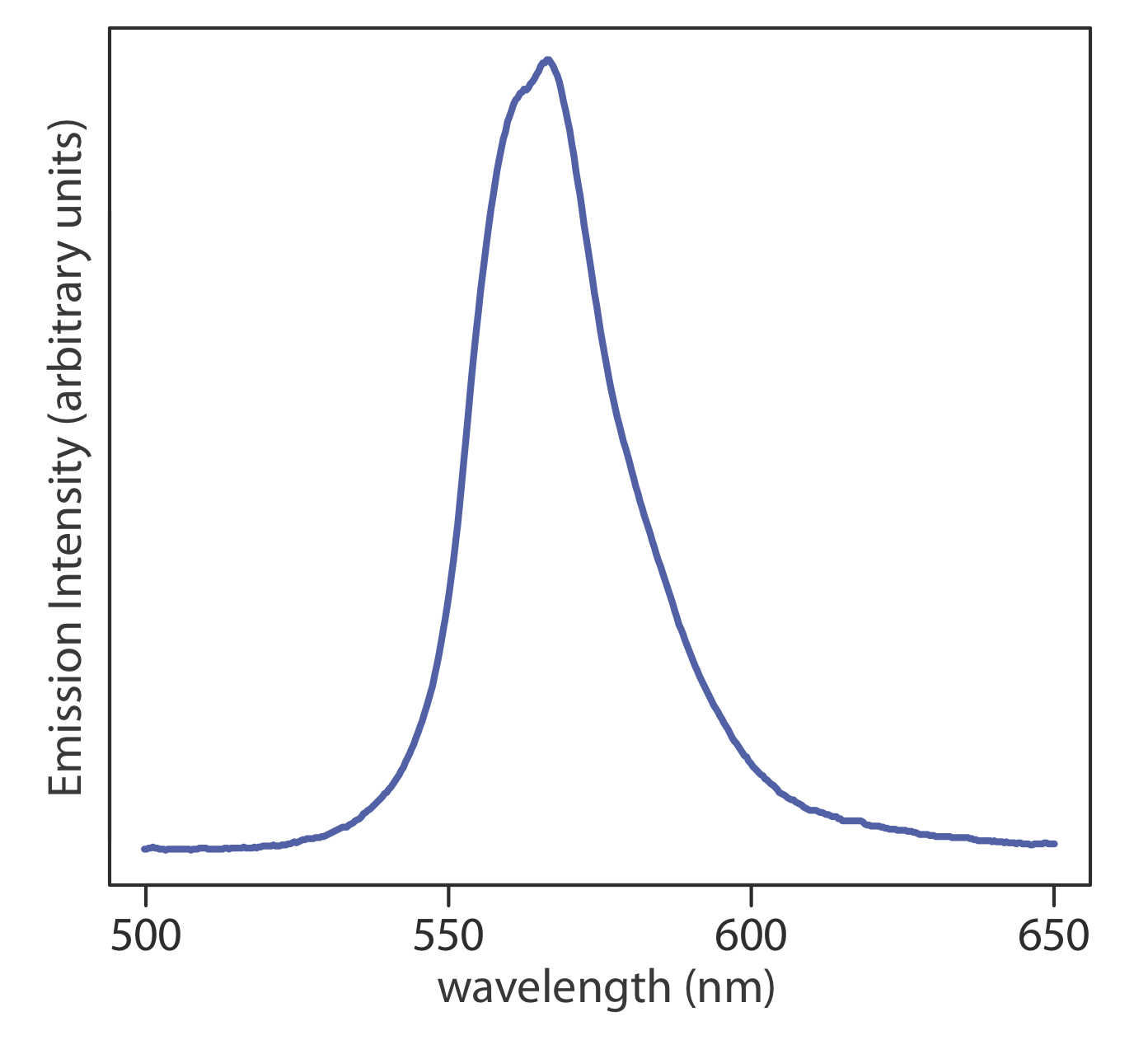
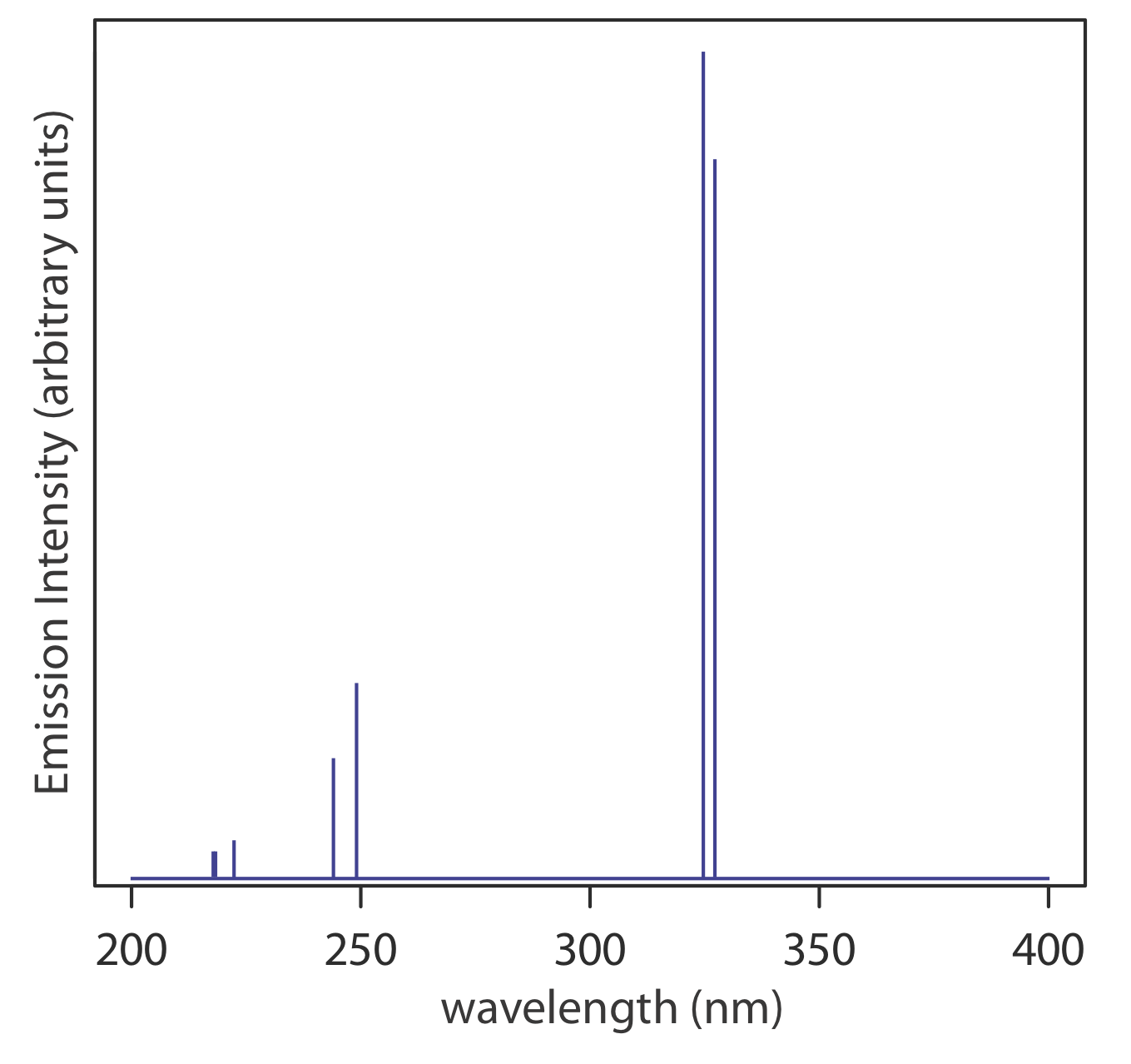
Fuentes de Radiación Electromagnética. Una fuente de radiación electromagnética debe proporcionar una salida que sea a la vez intensa y estable. Las fuentes de radiación electromagnética se clasifican como fuentes continuas o lineales. Una fuente continua emite radiación en un amplio rango de longitudes de onda, con una variación relativamente suave en la intensidad (Figura 10.1.7 ). Una fuente lineal, por otro lado, emite radiación a longitudes de onda seleccionadas (Figura 10.1.8 ). El cuadro 10.1.3 proporciona una lista de las fuentes más comunes de radiación electromagnética.
Fuentes de Radiación Térmica. Las fuentes más comunes de energía térmica son las llamas y los plasmas. Una fuente de llama utiliza una combustión de un combustible y un oxidante para lograr temperaturas de 2000—3400 K. Los plasmas, que son gases calientes, ionizados, proporcionan temperaturas de 6000—10000 K.
Fuentes Químicas de Energía. Las reacciones exotérmicas también pueden servir como fuente de energía. En la quimioluminiscencia el analito es elevado a un estado de mayor energía por medio de una reacción química, emitiendo radiación característica cuando vuelve a un estado de menor energía. Cuando la reacción química resulta de una reacción biológica o enzimática, la emisión de radiación se denomina bioluminiscencia. Las “barras de luz” disponibles comercialmente y el destello de luz de una luciérnaga son ejemplos de quimioluminiscencia y bioluminiscencia.
Selección de longitud de onda
En el método colorimétrico original de Nessler para el amoníaco, que se describió al inicio del capítulo, la muestra y varias soluciones estándar de amoníaco se colocan en tubos separados altos de fondo plano. Como se muestra en la Figura 10.1.9 , después de agregar los reactivos y permitir que se desarrolle el color, el analista evalúa el color pasando la luz ambiental por el fondo de los tubos y mirando hacia abajo a través de las soluciones. Al hacer coincidir el color de la muestra con el de un estándar, el analista es capaz de determinar la concentración de amoníaco en la muestra.
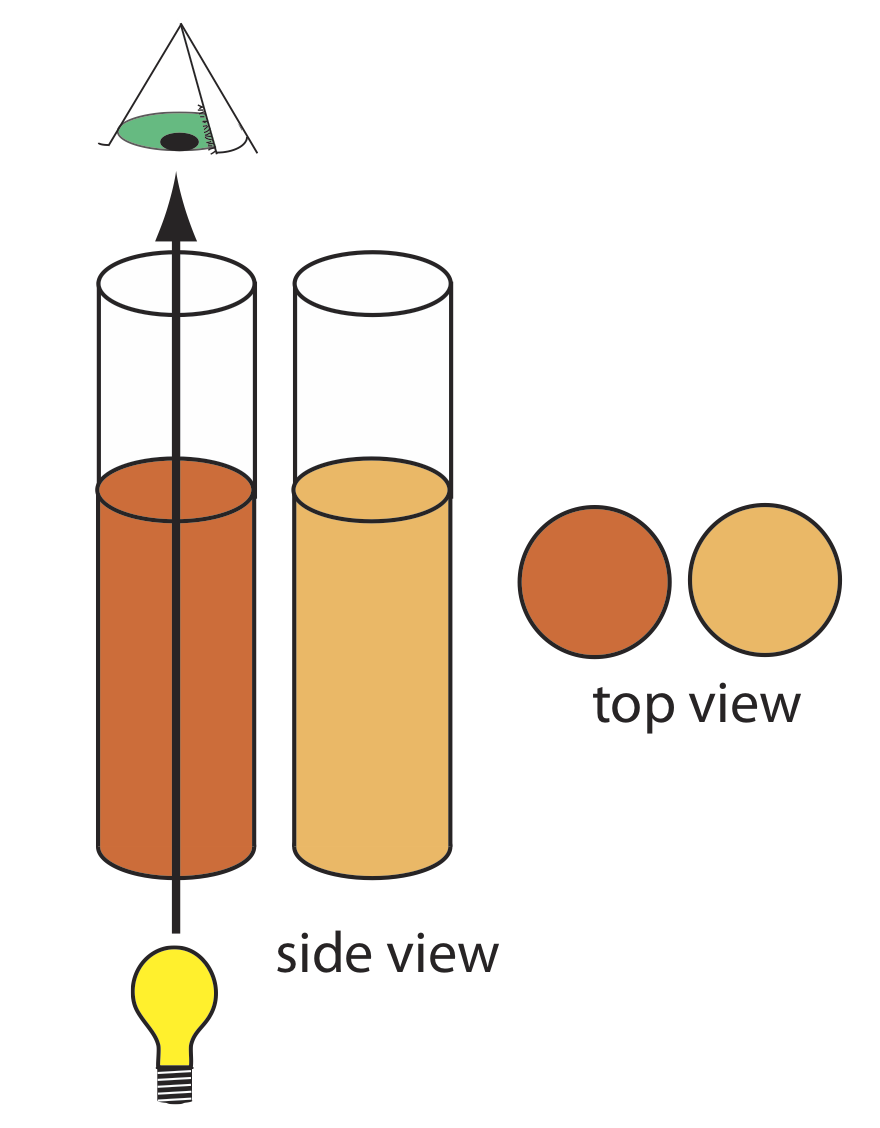
En la Figura 10.1.9 cada longitud de onda de luz de la fuente pasa a través de la muestra. Esto no es un problema si solo hay una especie absorbente en la muestra. Si la muestra contiene dos componentes, entonces un análisis cuantitativo utilizando el método original de Nessler es imposible a menos que los estándares contengan el segundo componente a la misma concentración que tiene en la muestra.
Para superar este problema, queremos seleccionar una longitud de onda que solo absorba el analito. Desafortunadamente, no podemos aislar una sola longitud de onda de radiación de una fuente continua, aunque podemos estrechar el rango de longitudes de onda que llegan a la muestra. Como se ve en la Figura 10.1.10 , un selector de longitud de onda siempre pasa por una banda estrecha de radiación caracterizada por una longitud de onda nominal, un ancho de banda efectivo y un rendimiento máximo de radiación. El ancho de banda efectivo se define como el ancho de la radiación a la mitad de su rendimiento máximo.
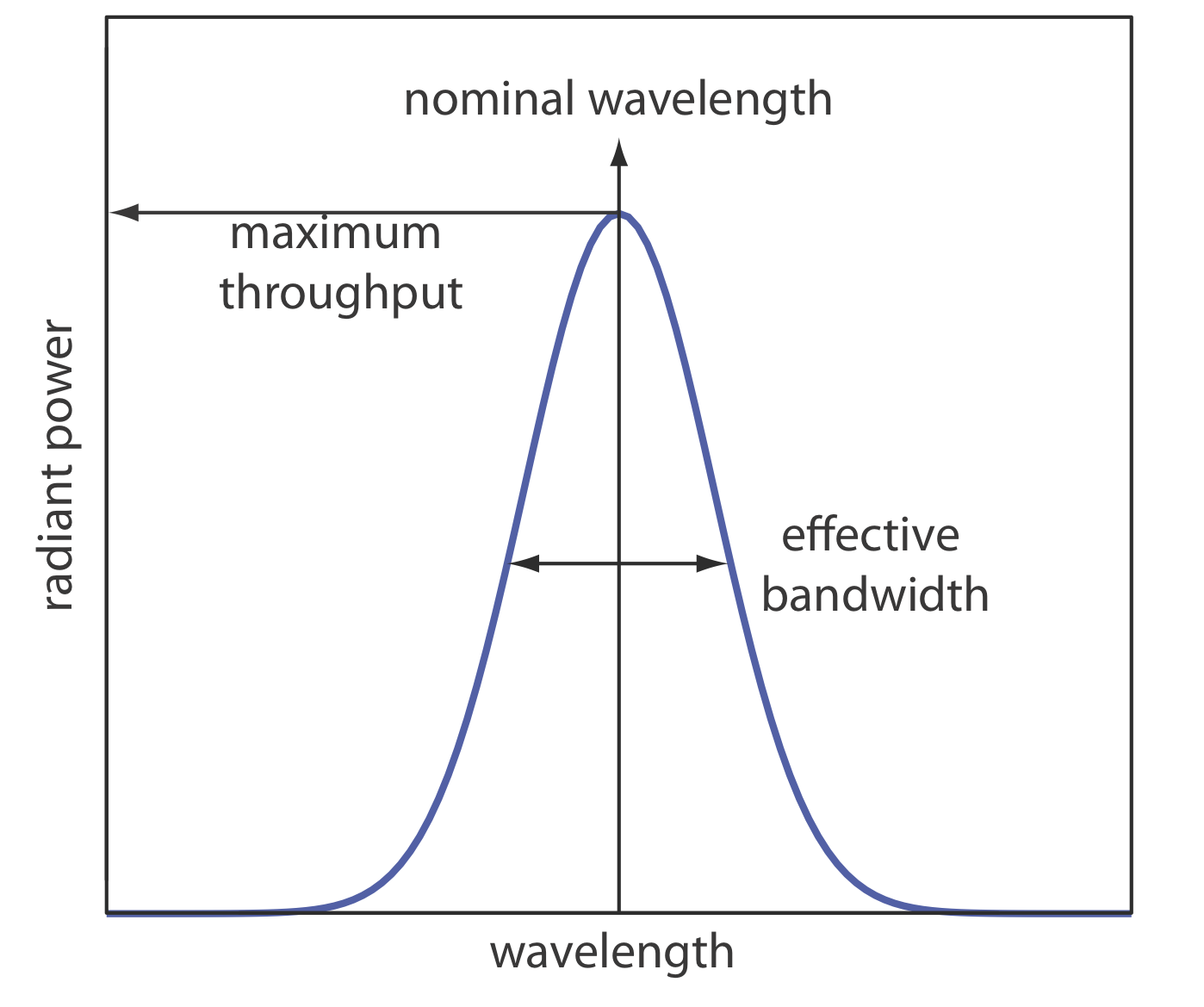
El selector de longitud de onda ideal tiene un alto rendimiento de radiación y un ancho de banda efectivo estrecho. Un alto rendimiento es deseable porque cuantos más fotones pasen a través del selector de longitud de onda, más fuerte será la señal y menor será el ruido de fondo. Un ancho de banda efectivo estrecho proporciona una resolución más alta, con características espectrales separadas por más del doble del ancho de banda efectivo que se resuelven. Como se muestra en la Figura 10.1.11 , estas dos características de un selector de longitud de onda a menudo están en oposición. Un ancho de banda efectivo mayor favorece un mayor rendimiento de radiación, pero proporciona menos resolución. Disminuir el ancho de banda efectivo mejora la resolución, pero a costa de una señal más ruidosa [Jiang, S.; Parker, G. A. Am. Laboratorio. 1981, octubre, 38—43]. Para un análisis cualitativo, la resolución suele ser más importante que el ruido y es deseable un ancho de banda efectivo menor; sin embargo, en un análisis cuantitativo suele ser deseable menos ruido.
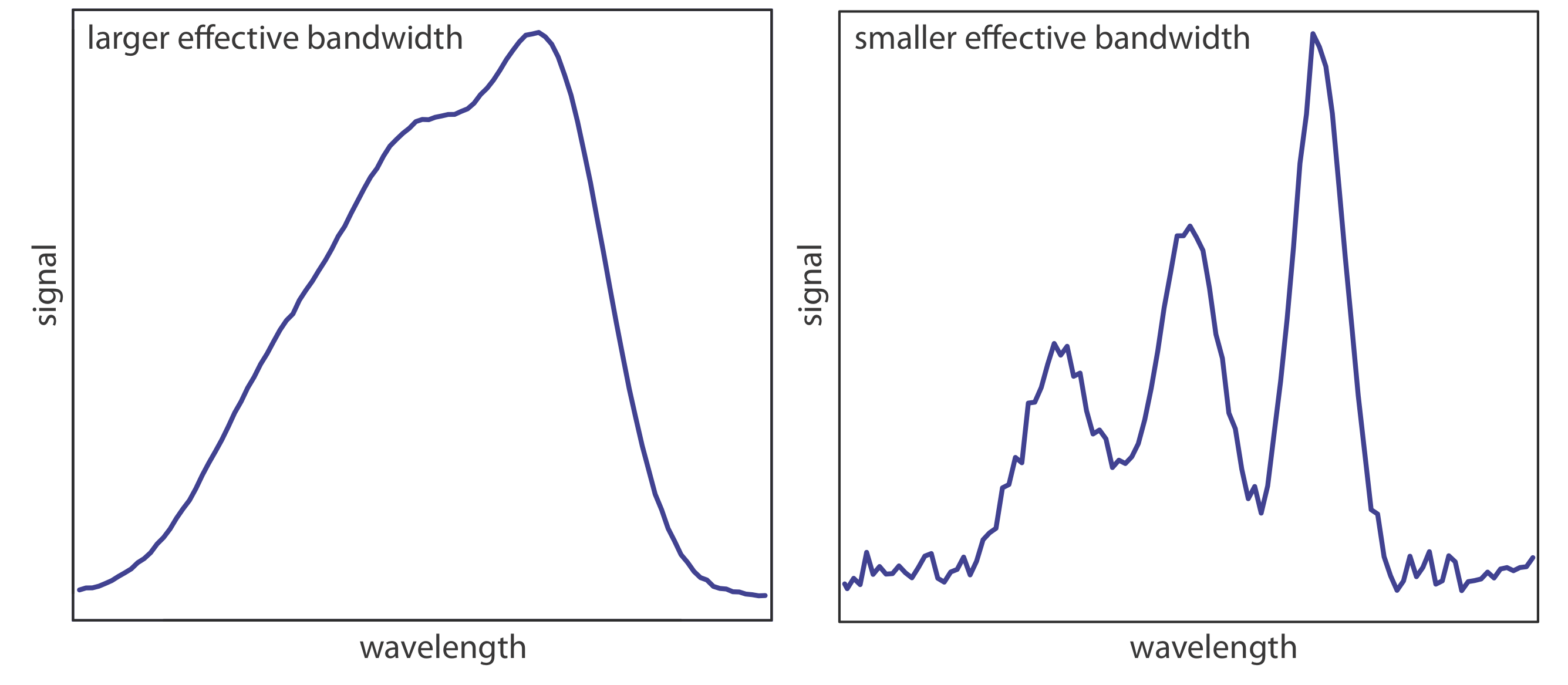
Selección de longitud de onda mediante filtros. El método más simple para aislar una banda estrecha de radiación es usar un filtro de absorción o interferencia. Los filtros de absorción funcionan absorbiendo selectivamente la radiación de una región estrecha del espectro electromagnético. Los filtros de interferencia utilizan interferencias constructivas y destructivas para aislar un rango estrecho de longitudes de onda. Un ejemplo sencillo de un filtro de absorción es un trozo de vidrio coloreado. Un filtro púrpura, por ejemplo, elimina el color complementario verde de 500 a 560 nm.
Los filtros de absorción disponibles comercialmente proporcionan anchos de banda efectivos de 30 a 250 nm, aunque el rendimiento en el extremo inferior de este rango a menudo es solo del 10% de la intensidad de emisión de la fuente. Los filtros de interferencia son más caros que los filtros de absorción, pero tienen anchos de banda efectivos más estrechos, típicamente 10—20 nm, con rendimientos máximos de al menos 40%.
Selección de Longitud de Onda Usando Monocromadores. Un filtro tiene una limitación significativa, ya que un filtro tiene una longitud de onda nominal fija, si necesitamos hacer mediciones a dos longitudes de onda diferentes, entonces debemos usar dos filtros diferentes. Un monocromador es un método alternativo para seleccionar una banda estrecha de radiación que también nos permite ajustar continuamente la longitud de onda nominal de la banda.
La construcción de un monocromador típico se muestra en la Figura 10.1.12 . La radiación de la fuente ingresa al monocromador a través de una hendidura de entrada. La radiación es recogida por un espejo colimador, que refleja un haz paralelo de radiación a una rejilla de difracción. La rejilla de difracción es una superficie ópticamente reflectante con un gran número de surcos paralelos (ver inserto en la Figura 10.1.12 ). La rejilla de difracción dispersa la radiación y un segundo espejo enfoca la radiación sobre una superficie plana que contiene una ranura de salida. En algunos monocromadores se utiliza un prisma en lugar de la rejilla de difracción.
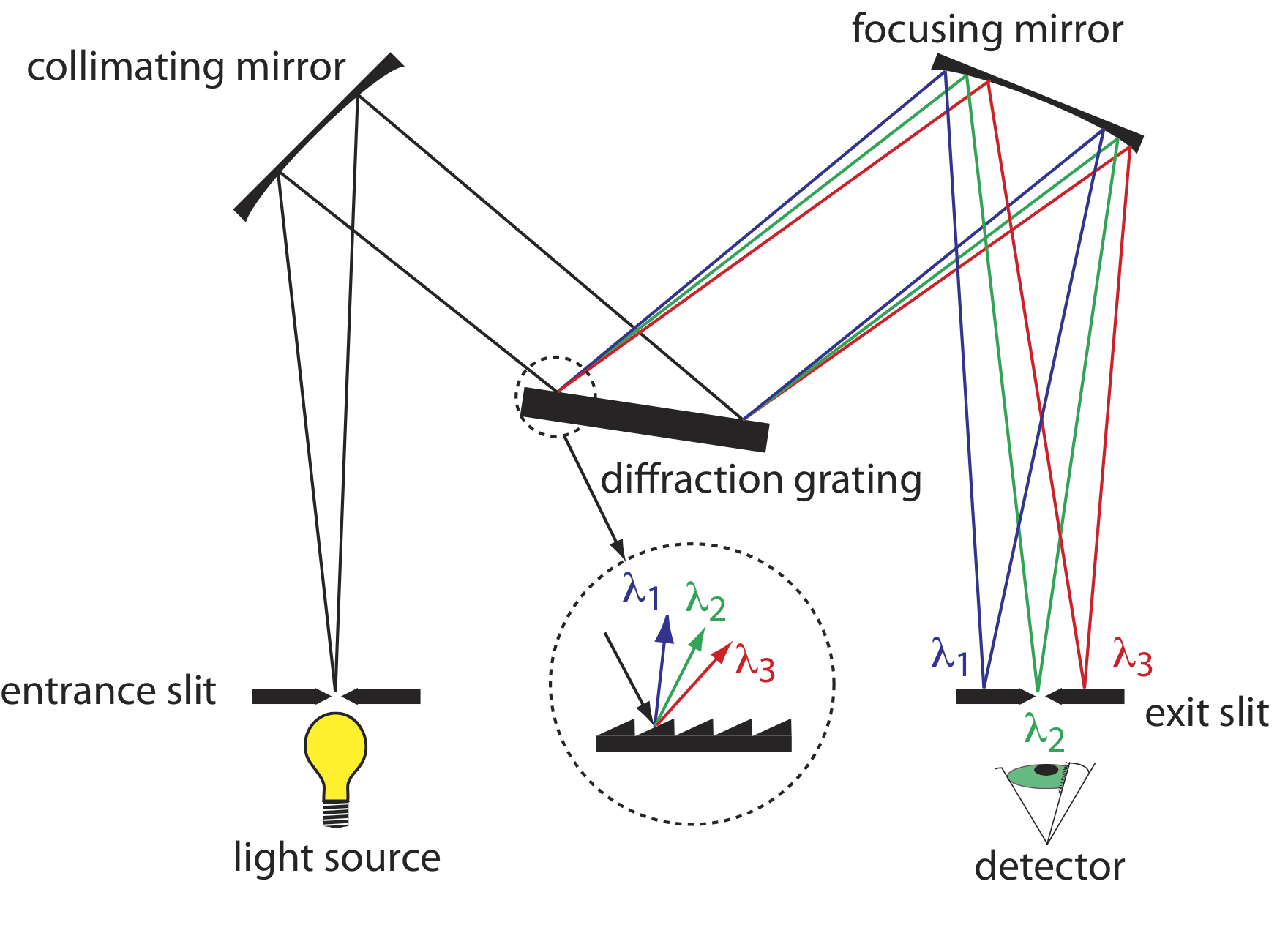
La radiación sale del monocromador y pasa al detector. Como se muestra en la Figura 10.1.12 , un monocromador convierte una fuente policromática de radiación en la hendidura de entrada en una fuente monocromática de ancho de banda efectivo finito en la ranura de salida. La elección de qué longitud de onda sale del monocromador se determina girando la rejilla de difracción. Una ranura de salida más estrecha proporciona un ancho de banda efectivo más pequeño y una mejor resolución que una ranura de salida más ancha, pero a costa de un menor rendimiento de radiación.
Policromático significa muchos colores. La radiación policromática contiene muchas longitudes de onda diferentes de luz. Monocromático significa un color, o una longitud de onda. Si bien la luz que sale de un monocromador no es estrictamente de una sola longitud de onda, su estrecho ancho de banda efectivo nos permite pensarlo como monocromática.
Los monocromadores se clasifican como longitud de onda fija o de barrido. En un monocromador de longitud de onda fija seleccionamos manualmente la longitud de onda girando la rejilla. Normalmente se utiliza un monocromador de longitud de onda fija para un análisis cuantitativo donde las mediciones se realizan a una o dos longitudes de onda. Un monocromador de exploración incluye un mecanismo de accionamiento que gira continuamente la rejilla, lo que permite que sucesivas longitudes de onda de luz salgan del monocromador. Se utiliza un monocromador de barrido para adquirir espectros y, cuando se opera en un modo de longitud de onda fija, para un análisis cuantitativo.
Interferómetros. Un interferómetro proporciona un enfoque alternativo para la selección de longitud de onda. En lugar de filtrar o dispersar la radiación electromagnética, un interferómetro permite que la radiación fuente de todas las longitudes de onda llegue al detector simultáneamente (Figura 10.1.13 ). La radiación de la fuente se enfoca en un divisor de haz que refleja la mitad de la radiación a un espejo fijo y transmite la otra mitad a un espejo en movimiento. La radiación se recombina en el divisor de haz, donde la interferencia constructiva y destructiva determina, para cada longitud de onda, la intensidad de la luz que llega al detector. A medida que el espejo móvil cambia de posición, la longitud de onda de la luz que experimenta la máxima interferencia constructiva y la máxima interferencia destructiva también cambia. La señal en el detector muestra la intensidad en función de la posición del espejo móvil, expresada en unidades de distancia o tiempo. El resultado se denomina interferograma o espectro en el dominio del tiempo. El espectro en el dominio del tiempo se convierte matemáticamente, mediante un proceso llamado transformada de Fourier, en un espectro (un espectro de dominio de frecuencia) que muestra la intensidad en función de la energía de la radiación.
Los detalles matemáticos de la transformada de Fourier están más allá del nivel de este libro de texto. Puede consultar los recursos adicionales del capítulo para obtener información adicional.
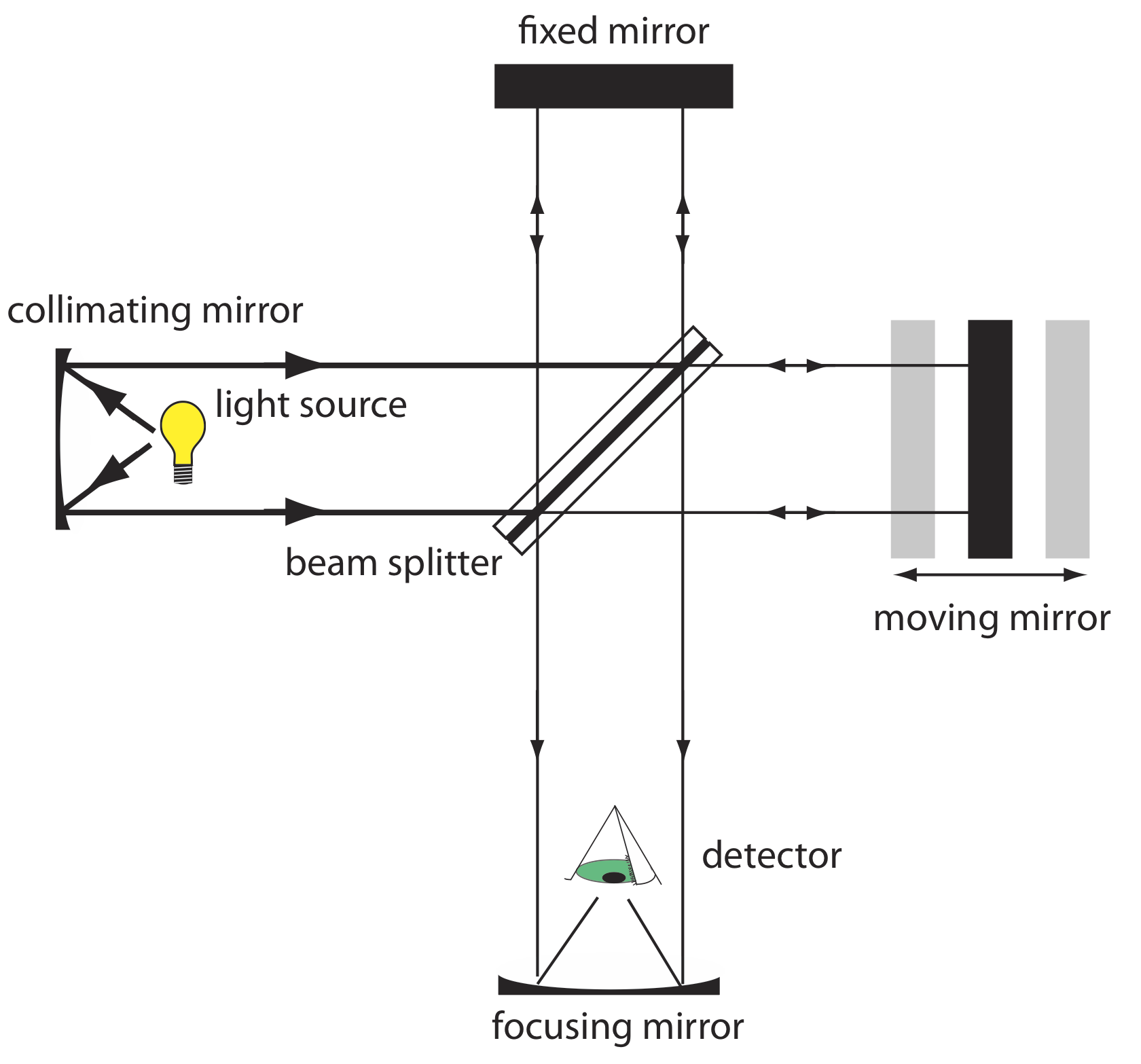
En comparación con un monocromador, un interferómetro tiene dos ventajas significativas. La primera ventaja, que se denomina ventaja de Jacquinot, es el mayor rendimiento de radiación fuente. Debido a que un interferómetro no utiliza hendiduras y tiene menos componentes ópticos de los cuales se dispersa y pierde la radiación, el rendimiento de radiación que llega al detector es\(80-200 \times\) mayor que el de un monocromador. El resultado es menos ruido. La segunda ventaja, que se llama ventaja de Fellgett, es un ahorro en el tiempo necesario para obtener un espectro. Debido a que el detector monitorea todas las frecuencias simultáneamente, un espectro tarda aproximadamente un segundo en grabarse, en comparación con 10 a 15 minutos cuando se usa un monocromador de escaneo.
Detectores
En el método original de Nessler para determinar el amoníaco (Figura 10.1.9 ) el ojo del analista sirve como detector, haciendo coincidir el color de la muestra con el de un estándar. El ojo humano, por supuesto, tiene un rango pobre —responde solo a la luz visible— y no es particularmente sensible ni preciso. Los detectores modernos utilizan un transductor sensible para convertir una señal que consiste en fotones en una señal eléctrica de fácil medición. Idealmente, la señal del detector, S, es una función lineal de la potencia de la radiación electromagnética, P,
\[S=k P+D \nonumber\]
donde k es la sensibilidad del detector, y D es la corriente oscura del detector, o la corriente de fondo cuando evitamos que la radiación de la fuente llegue al detector.
Hay dos clases amplias de transductores espectroscópicos: transductores térmicos y transductores de fotones. La Tabla 10.1.4 proporciona varios ejemplos representativos de cada clase de transductores.
Transductor es un término general que se refiere a cualquier dispositivo que convierta una propiedad química o física en una señal eléctrica de fácil medición. La retina en tu ojo, por ejemplo, es un transductor que convierte los fotones en un impulso nervioso eléctrico; tu tímpano es un transductor que convierte las ondas sonoras en un impulso nervioso eléctrico diferente.
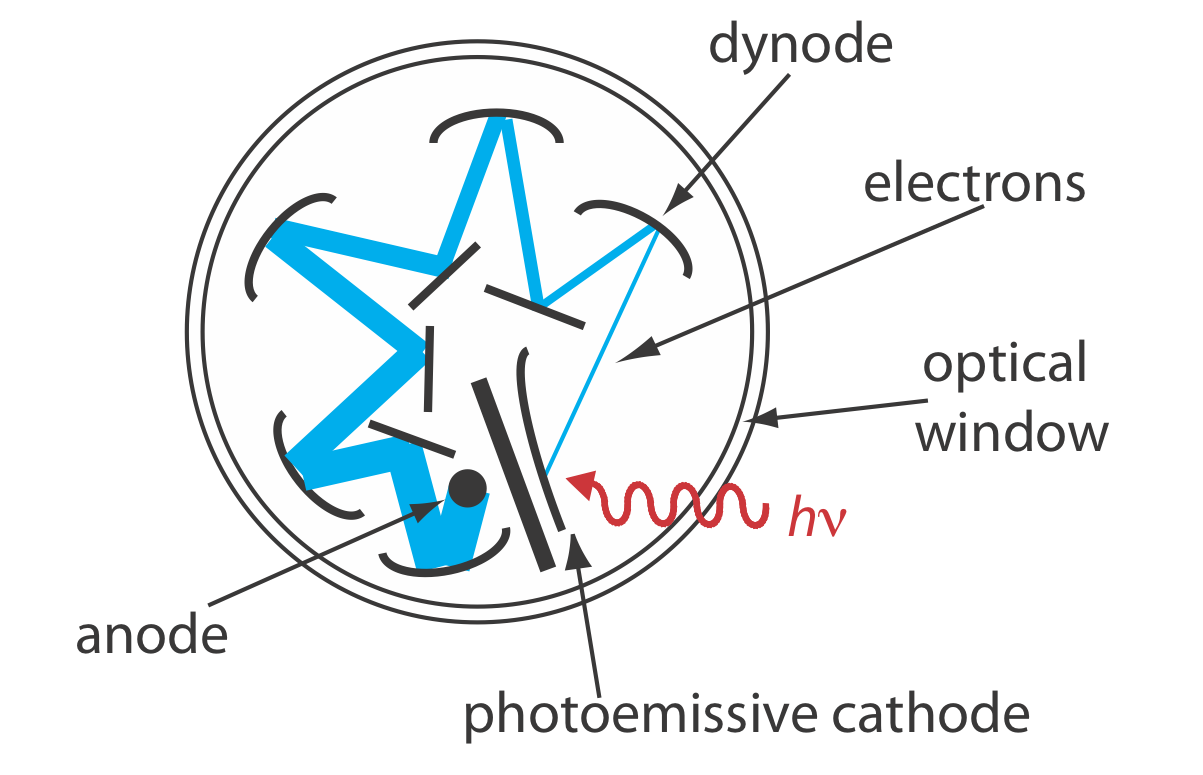
Transductores de Fotones. Los fototubos y fotomultiplificadores utilizan una superficie fotosensible que absorbe radiación en el ultravioleta, visible o IR cercano para producir una corriente eléctrica que es proporcional al número de fotones que llegan al transductor (Figura 10.1.14 ). Otros detectores de fotones utilizan un semiconductor como superficie fotosensible. Cuando el semiconductor absorbe fotones, los electrones de valencia se mueven a la banda de conducción del semiconductor, produciendo una corriente medible. Una ventaja del fotodiodo Si es que es fácil de miniaturizar. Los grupos de fotodiodos se reúnen en una matriz lineal que contiene 64—4096 fotodiodos individuales. Con un ancho de 25 μm por diodo, una matriz lineal de 2048 fotodiodos requiere solo 51.2 mm de espacio lineal. Al colocar una matriz de fotodiodos a lo largo del plano focal del monocromador, es posible monitorear simultáneamente un rango completo de longitudes de onda.
Transductores Térmicos. Los fotones infrarrojos no tienen suficiente energía para producir una corriente medible con un transductor de fotones. Un transductor térmico, por lo tanto, se utiliza para la espectroscopia infrarroja. La absorción de fotones infrarrojos aumenta la temperatura de un transductor térmico, cambiando una o más de sus propiedades características. Un transductor neumático, por ejemplo, es un pequeño tubo de gas xenón con una ventana transparente IR en un extremo y una membrana flexible en el otro extremo. Los fotones entran al tubo y son absorbidos por una superficie ennegrecida, aumentando la temperatura del gas. A medida que la temperatura dentro del tubo fluctúa, el gas se expande y se contrae y la membrana flexible entra y sale. El monitoreo del desplazamiento de la membrana produce una señal eléctrica.
Procesadores de señal
La señal eléctrica de un transductor se envía a un procesador de señales donde se muestra en una forma que es más conveniente para el analista. Ejemplos de procesadores de señal incluyen medidores analógicos o digitales, grabadoras y computadoras equipadas con placas de adquisición digital. Un procesador de señal también se utiliza para calibrar la respuesta del detector, para amplificar la señal del transductor, para eliminar el ruido filtrando, o para transformar matemáticamente la señal.
Si la retina en tu ojo y el tímpano en tu oído son transductores, entonces tu cerebro es el procesador de señales.