5.4: Modelado de distribuciones usando R

Última actualización
Guardar como PDF

Page ID: 69303

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La instalación base de R incluye una variedad de funciones para trabajar con distribuciones uniformes, distribuciones binomiales, distribuciones de Poisson y distribuciones normales. Estas funciones vienen en cuatro formas que toman la forma general xdist donde dist es el tipo de distribución (unif para una distribución uniforme, binom para una distribución binomial, pois para una distribución de Poisson y norma para una normal distribución), y donde x define la información que extraemos de la distribución. Por ejemplo, la función dunif () devuelve la probabilidad de obtener un valor específico extraído de una distribución uniforme, la función pbinom () devuelve la probabilidad de obtener un resultado menor que un valor definido a partir de una distribución binomial, la función qpois () devuelve el límite superior que incluye un porcentaje definido de resultados de una distribución de Poisson, y la función rnomr () devuelve resultados dibujados al azar a partir de una distribución normal.

Modelado de una Distribución Uniforme Usando R

Cuando compra una pipeta volumétrica Clase A de 10.00 mL viene con una tolerancia de ±0.02 mL, que es la manera del fabricante de decir que el verdadero volumen de la pipeta no es menor de 9.98 mL y no mayor de 10.02 mL. Supongamos que un fabricante produce 10,000 pipetas, ¿cuántas podríamos esperar tener un volumen entre 9.990 mL y 9.992 mL? Una distribución uniforme es la elección cuando el fabricante proporciona un rango de tolerancia sin especificar un nivel de confianza y cuando no hay razón para creer que los resultados cerca del centro del rango son más probables que los resultados en los extremos del rango.

Para simular una distribución uniforme utilizamos la función runif (n, min, max) de R, que devuelve n valores aleatorios dibujados a partir de una distribución uniforme definida por sus límites mínimo (min) y máximo (max). El resultado se muestra en la Figura$\PageIndex{1}$, donde los puntos, agregados mediante la función points (), muestran la distribución uniforme teórica en el punto medio de cada uno de los bins del histograma.

# crear vector de volúmenes para 10000 pipetas dibujadas al azar a partir de una distribución uniforme

pipeta = runif (10000, 9.98, 10.02)

# crear histograma usando 20 bins de tamaño 0.002 mL

pipet_hist = hist (pipeta, roturas = seq (9.98, 10.02, 0.002), col = c (“azul”, “celeste”), ylab = “número de pipetas”, xlab = “volumen de pipeta (mL)”, main = NULL)

# puntos de superposición que muestran valores esperados para una distribución uniforme

puntos (pipet_hist$medios, rep (10000/20, 20), pch = 19)

Figura$\PageIndex{1}$: Distribución uniforme de volúmenes para 10000 pipetas volumétricas de 10 ml. Las barras individuales muestran los resultados simulados y los puntos individuales muestran los resultados esperados.

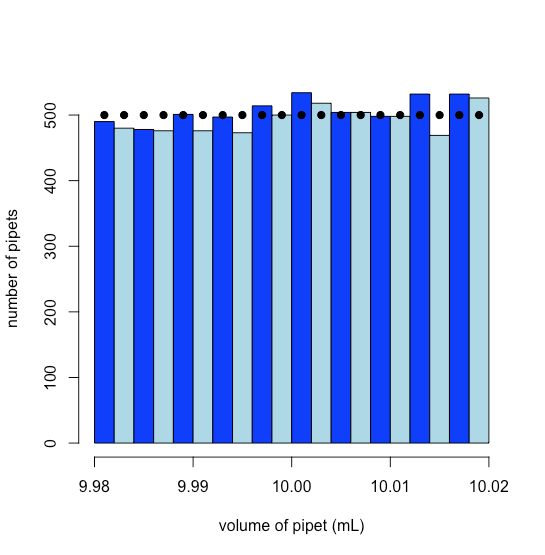
Guardar el histograma en el objeto pipet_hist nos permite recuperar el número de pipetas en cada uno de los intervalos del histograma; así, hay 476 pipetas con volúmenes entre 9.990 mL y 9.992 mL, que es la sexta barra desde el borde izquierdo de la Figura$\PageIndex{1}$.

pipet_hist$recuentos [6]

[1] 476

Modelado de una Distribución Binomial Usando R

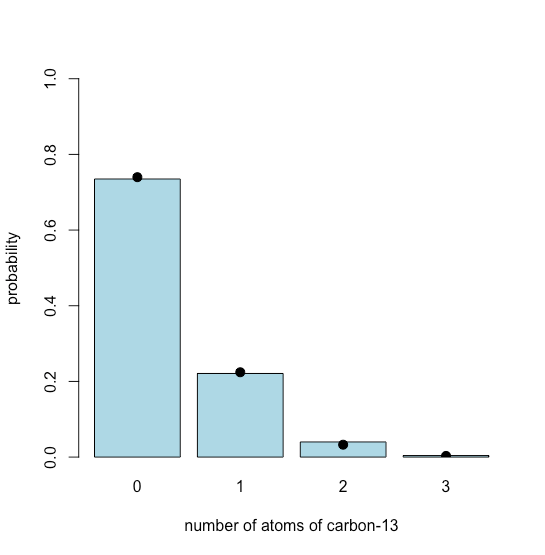
El carbono tiene dos isótopos estables, no radiactivos, ¹² C y ¹³ C, con abundancias isotópicas relativas de 98.89% y 1.11% respectivamente. Supongamos que estamos trabajando con colesterol, C ₂₇ H ₄₄ O, que tiene 27 átomos de carbono. Podemos utilizar la distribución binomial para modelar la distribución esperada para el número de átomos ¹³ C en 1000 moléculas de colesterol.

Para simular la distribución utilizamos la función rbinom (n, size, prob) de R, que devuelve n valores aleatorios extraídos de una distribución binomial definida por el tamaño de nuestra muestra, que es el número de átomos de carbono posibles, y la abundancia isotópica de ¹³ C, que es su problema o probabilidad. El resultado se muestra en la Figura$\PageIndex{2}$, donde los puntos, agregados usando la función points (), muestran la distribución binomial teórica. Estos valores teóricos se calculan utilizando la función dbinom (). La gráfica de barras se asigna al objeto chol.bar para proporcionar acceso a los valores de x al trazar los puntos.

# crear vector con 1000 valores dibujados al azar a partir de la distribución binomial

colesterol = rbinom (1000, 27, 0.0111)

# crear gráfico de barras de resultados; tabla (colesterol) determina el número de colesterol

# moléculas con 0, 1, 2... átomos de carbono-13; dividiendo por 1000 da probabilidad

chol_bar = barplot (tabla (colesterol) /1000, col = “azul claro”, ylim = c (0,1), xlab = “número de átomos de carbono-13", ylab = “probabilidad”)

# resultados teóricos para la distribución binomial de carbono-13 en colesterol

chol_binom = dbinom (seq (0,27,1), 27, 0.0111)

# superposición de resultados teóricos para la distribución binomial

puntos (x = chol_bar, y = chol.binom [1:longitud (chol_bar)], cex = 1.25, pch = 19)

Figura$\PageIndex{2}$: Distribución de los resultados para átomos de carbono 13 en colesterol. Las barras individuales muestran los resultados simulados y los puntos individuales muestran los resultados esperados.

Modelado de una Distribución de Poisson Usando R

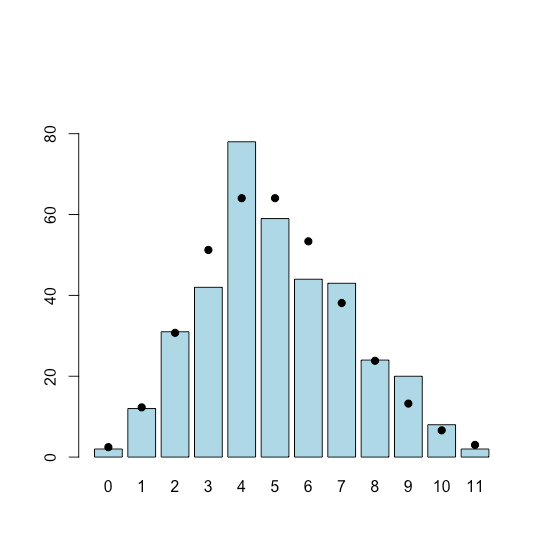
Una medida de la calidad del agua en lagos utilizados con fines recreativos es una prueba coliforme fecal. En una prueba típica se pasa una muestra de agua a través de un filtro de membrana, el cual luego se coloca en un medio para fomentar el crecimiento de la bacteria y se incuba durante 24 horas a 44.5°C, se reporta el número de colonias de bacterias. Supongamos que un lago tiene un nivel de fondo natural de 5 colonias por cada 50 mL de agua probada y debe ser cerrado para nadar si supera las 10 colonias por cada 50 mL de agua probada. Podemos usar una distribución de Poisson para determinar, en el transcurso de un año de pruebas diarias, la probabilidad de que una prueba supere este límite aunque el verdadero recuento de coliformes fecales del lago permanezca en su nivel de fondo natural.

Para simular la distribución utilizamos la función rpois (n, lambda) de R, que devuelve n valores aleatorios extraídos de una distribución de Poisson definida por lambda que es su incidencia promedio. Debido a que estamos interesados en modelar un año, n se establece en 365 días. El resultado se muestra en la Figura$\PageIndex{3}$, donde los puntos, agregados usando la función points (), muestran la distribución teórica de Poisson. Estos valores teóricos se calculan utilizando la función dpois (). El gráfico de barras se asigna al objeto choliform.bar para proporcionar acceso a los valores de x al trazar los puntos.

# crear vector de resultados dibujados al azar a partir de la distribución de Poisson

coliformes = rpois (365,5)

# crear tabla de resultados simulados

coliform_table = tabla (coliformes)

# crear parcela de barra; ylim asegura que haya algo de espacio por encima de la barra más alta de la parcela

coliform_bar = barplot (coliform_table, ylim = c (0, 1.2 * max (coliform_table)), col = “celeste”)

# resultados teóricos para la distribución de Poisson

d_coliformes = dpois (seq (0, longitud (coliform_bar) - 1), 5) * 365

# resultados teóricos de superposición para la distribución de Poisson

puntos (coliform_bar, d_coliforms, pch = 19)

Figura$\PageIndex{3}$: Distribución de los resultados de la prueba coliforme fecal a lo largo de un año. Las barras individuales muestran los resultados simulados y los puntos individuales muestran los resultados esperados.

Para encontrar el número de veces que nuestros resultados simulados superan el límite de 10 colonias de coliformes por 50 mL utilizamos R que () funcionan para identificar dentro de los coliformes los valores que son mayores a 10

coliformes [que (coliformes > 10)]

encontrando que esto suceda 2 veces en el transcurso de un año.

La probabilidad teórica de que una sola prueba supere el límite de 10 colonias por 50 mL de agua, utilizamos la función ppois (q, lambda) de R, donde q es el valor que deseamos probar, lo que devuelve la probabilidad acumulada de obtener un resultado menor o igual a q on cualquier día; en el transcurso de 365 días

(1 - ppois (10,5)) *365

[1] 4.998773

esperamos que en 5 días el recuento de coliformes fecales supere el límite de 10.

Modelado de una Distribución Normal Usando R

Si colocamos cobre metálico y un exceso de azufre en polvo en un crisol y lo encendemos, el sulfuro de cobre se forma con una fórmula empírica de Cu _x S. El valor de x se determina pesando el Cu y el S antes de la ignición y encontrando la masa de Cu _x S cuando se completa la reacción (cualquier exceso de azufre sale como el gas SO ₂). Las siguientes son las relaciones Cu/S de 62 experimentos de este tipo, de los cuales solo 3 son mayores que 2. Debido al teorema del límite central, podemos usar una distribución normal para modelar los datos.

Cuadro$\PageIndex{1}$: Relaciones Cu/S experimentales al encender Cu (s) y S (s).
1.764	1.838	1.890	1.891	1.906	1.908
1.920	1.922	1.936	1.937	1.941	1.942
1.957	1.957	1.963	1.963	1.975	1.976
1.993	1.993	2.029	2.042	1.866	1.872
1.891	1.897	1.899	1.910	1.911	1.916
1.927	1.931	1.935	1.939	1.939	1.940
1.943	1.948	1.953	1.957	1.959	1.962
1.966	1.968	1.969	1.977	1.981	1.981
1.995	1.995	1.865	1.995	1.877	1.900
1.919	1.936	1.941	1.955	1.963	1.973
1.988	2.017

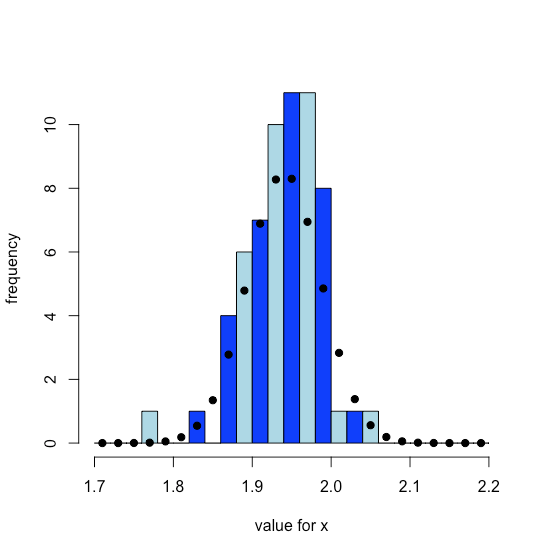
La figura$\PageIndex{4}$ muestra la distribución de los resultados experimentales como un histograma superpuesto con la distribución normal teórica calculada asumiendo que$\mu$ es igual a la media de las 62 muestras y que$\sigma$ es igual a la desviación estándar de las 62 muestras. Tanto los datos experimentales como la distribución teórica normal sugieren que la mayoría de los valores de x están entre 1.85 y 2.03.

# introducir los datos en un vector con el nombre cuxs

cuxs = c (1.764, 1.920, 1.957, 1.993, 1.891, 1.927, 1.943, 1.966, 1.995, 1.919, 1.988, 1.838, 1.922, 1.957, 1.993, 1.897, 1.931, 1.948, 1.968, 1.995, 1.936, 2.017, 1.890, 1.936, 1.963, 2.029, 1.899, 1.935, 1.953, 1.969, 1.865, 1.941, 1.891, 1.937, 1.963, 2.042, 1.910, 1.939, 1.957, 1.977, 1.995, 1.955, 1 .906, 1.941, 1.975, 1.866, 1.911, 1.939, 1.959, 1.981, 1.877, 1.963, 1.908, 1.942, 1.976, 1.872, 1.916, 1.940, 1.962, 1.981, 1.900, 1.973)

# secuencia de proporciones sobre las cuales mostrar resultados experimentales y distribución teórica

x = seq (1.7,2.2,0.02)

# crear histograma para resultados experimentales

cuxs_hist = hist (cuxs, breaks = x, col = c (“azul”, “celeste”), xlab = “valor para x”, ylab = “frecuencia”, main = NULL)

# calcular los resultados teóricos para la distribución normal usando la media y la desviación estándar

# para las 62 muestras como predictores para mu y sigma

cuxs_theo = dnorm (cuxs_hist$medios, media = media (cuxs), sd = sd (cuxs))

# resultados de superposición para la distribución normal teórica

puntos (cuxs_hist$medios, cuxs_theo, pch = 19)

Figura$\PageIndex{4}$: Distribución de resultados para relación de Cu a S en preparaciones de sulfuro de cobre. Las barras individuales muestran los resultados simulados y los puntos individuales muestran los resultados esperados.