8.5: Uso de R para un análisis de regresión lineal
- Page ID
- 69360
En la Sección 8.1 se utilizaron los datos de la tabla siguiente para trabajar a través de los detalles de un análisis de regresión lineal donde los valores de\(x_i\) son las concentraciones de analito\(C_A\),, en una serie de soluciones estándar, y donde los valores de\(y_i\), son sus señales medidas,\(S\). Usemos R para modelar estos datos usando la ecuación para una línea recta.
\[y = \beta_0 + \beta_1 x \nonumber\]
| \(x_i\) | \(y_i\) |
|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12.36 |
| \ (x_i\) ">0.200 | \ (y_i\) ">24.83 |
| \ (x_i\) ">0.300 | \ (y_i\) ">35.91 |
| \ (x_i\) ">0.400 | \ (y_i\) ">48.79 |
| \ (x_i\) ">0.500 | \ (y_i\) ">60.42 |
Ingresar Datos en R
Para comenzar, creamos dos objetos, uno que contiene la concentración de los estándares y otro que contiene sus señales correspondientes.
conc = c (0, 0.1, 0.2, 0.3, 0.4, 0.5)
señal = c (0, 12.36, 24.83, 35.91, 48.79, 60.42)
Creación de un modelo lineal en R
Un modelo lineal en R se define usando la sintaxis general
variable dependiente ~ variable (s) independiente (es)
Por ejemplo, la sintaxis para un modelo con la ecuación\(y = \beta_0 + \beta_1 x\), donde\(\beta_0\) y\(\beta_1\) son los parámetros ajustables del modelo, es\(y \sim x\). \(\PageIndex{2}\)La tabla proporciona algunos ejemplos adicionales donde\(A\) y\(B\) son variables independientes, como las concentraciones de dos analitos, y\(y\) es una variable dependiente, como una señal medida.
| modelo | sintaxis | comentarios sobre model |
|---|---|---|
| \(y = \beta_a A\) | \(y \sim 0 + A\) | línea recta forzada a través (0, 0) |
| \(y = \beta_0 + \beta_a A\) | \(y \sim A\) | línea de combate con una intercepción y |
| \(y = \beta_0 + \beta_a A + \beta_b B\) | \(y \sim A + B\) | de primer orden en A y B |
| \(y = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB\) | \(y \sim A * B\) | primer orden en A y B con interacción AB |
| \(y = \beta_0 + \beta_{ab} AB\) | \(y \sim A:B\) | Solo interacción AB |
| \(y = \beta_0 + \beta_a A + \beta_{aa} A^2\) | \(y \sim A + I(A\text{^2})\) | polinomio de segundo orden |
La última fórmula de esta tabla,\(y \sim A + I(A\text{^2})\), incluye la función I (), o ASis. Una complicación con la escritura de fórmulas es que utilizan símbolos que tienen significados diferentes en las fórmulas que tienen en una ecuación matemática. Por ejemplo, tomemos la fórmula simple\(y \sim A + B\) que corresponde al modelo\(y = \beta_0 + \beta_a A + \beta_b B\). Tenga en cuenta que el signo más aquí construye una fórmula que tiene una intercepción y un término para\(A\) y un término para\(B\). Pero, ¿y si quisiéramos construir un modelo que usara la suma de\(A\) y\(B\) como la variable? Envolver\(A+B\) dentro de la función I () logra esto; así\(y \sim I(A + B)\) construye el modelo\(y = \beta_0 + \beta_{a+b} (A + B)\).
Para crear nuestro modelo utilizamos la función lm (), donde lm significa modelo lineal, asignando los resultados a un objeto para que podamos acceder a ellos más tarde.
calcurve = lm (señal ~ conc)
Evaluación del Modelo de Regresión Lineal
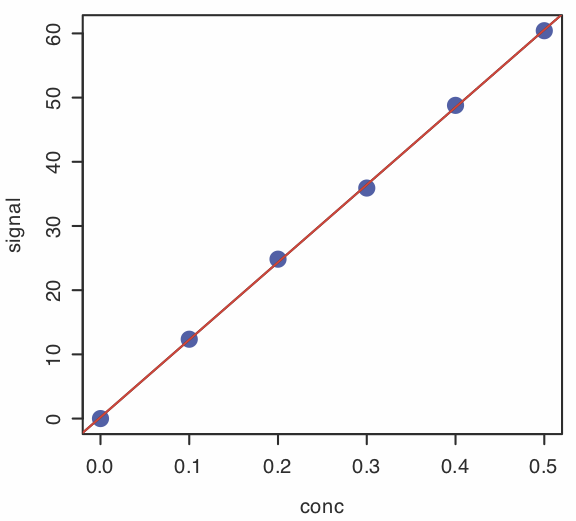
Para evaluar los resultados de una regresión lineal necesitamos examinar los datos y la línea de regresión, y revisar un resumen estadístico del modelo. Para examinar nuestros datos y la línea de regresión, utilizamos la función plot (), introducida por primera vez en el Capítulo 3, que toma la siguiente forma general
parcela (x, y,...)
donde x e y son los objetos que contienen nuestros datos y el... permiten pasar argumentos opcionales para controlar el estilo de la trama. Para superponer la curva de regresión, usamos la función abline ()
abline (objeto,...)
objeto es el objeto que contiene los resultados del modelo de regresión lineal y el... permiten pasar argumentos opcionales para controlar el estilo del modelo. Ingresando los comandos
plot (conc, señal, pch = 19, col = “azul”, cex = 2)
abline (calcurve, col = “rojo”, lty = 2, lwd = 2)
crea la gráfica mostrada en la Figura\(\PageIndex{1}\).
La función abline () solo funciona con un modelo de línea recta.
Para revisar un resumen estadístico del modelo de regresión, utilizamos la función summary ().
resumen (calcurve)
El resultado resultante, que se muestra a continuación, contiene tres secciones.
Llamar a:
lm (fórmula = señal ~ conc)
Residuales:
1 2 3 4 5 6
-0.20857 0.08086 0.48029 -0.51029 0.29914 -0.14143
Coeficientes:
Estimación Std. Error t valor Pr (>|t|)
(Intercepción) 0.2086 0.2919 0.715 0.514
conc 120.7057 0.9641 125.205 2.44e-08 ***
—
Signif. códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '' 1
Error estándar residual: 0.4033 en 4 grados de libertad
R al cuadrado múltiple: 0.9997, R cuadrado ajustado: 0.9997
Estadístico F: 1.568e+04 sobre 1 y 4 DF, valor p: 2.441e-08
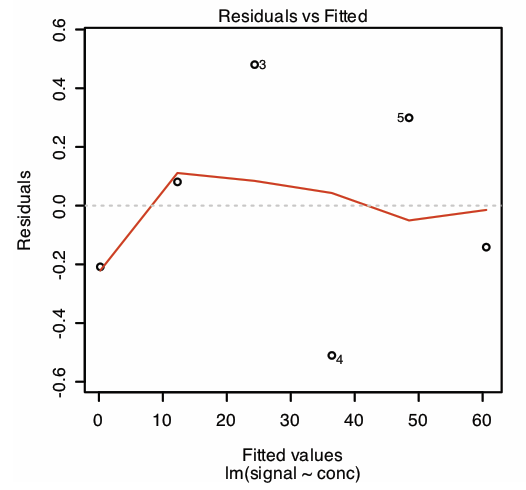
En la primera sección de este resumen se enumeran los errores residuales. Para examinar una gráfica de los errores residuales, utilice el comando
plot (calcurve, que = 1)
lo que produce el resultado mostrado en la Figura\(\PageIndex{2}\). Obsérvese que R traza los residuos contra los valores predichos (ajustados) de y en lugar de contra los valores conocidos de x, como hicimos en la Sección 8. 1; la elección de cómo trazar los residuos no es crítica. La línea en la Figura\(\PageIndex{2}\) es un ajuste suavizado de los residuos.
La razón para incluir el argumento que = 1 no es inmediatamente evidente. Cuando se utiliza la función plot () de R en un objeto creado usando lm (), el valor predeterminado es crear cuatro gráficos que resuman la idoneidad del modelo. La primera de estas gráficas es la gráfica residual; así, que = 1 limita la salida a esta gráfica.
La segunda sección del resumen proporciona estimaciones para los coeficientes del modelo, la pendiente\(\beta_1\), y la intersección y,\(\beta_0\) junto con sus respectivas desviaciones estándar (Std. Error). El valor de la columna t y la columna Pr (>|t|) son los valores p para las siguientes pruebas t.
pendiente:\(H_0 \text{: } \beta_1 = 0 \quad H_A \text{: } \beta_1 \neq 0\)
y -interceptar:\(H_0 \text{: } \beta_0 = 0 \quad H_A \text{: } \beta_0 \neq 0\)
Los resultados de estas pruebas t proporcionan evidencia convincente de que la pendiente no es cero y ninguna evidencia de que la intersección y difiera significativamente de cero.
La última sección del resumen proporciona la desviación estándar sobre la regresión (error estándar residual), el cuadrado del coeficiente de correlación (R-cuadrado múltiple) y el resultado de una prueba F sobre la capacidad del modelo para explicar la variación en la y valores.
El valor para el estadístico F es el resultado de una prueba F de las siguientes hipótesis nulas y alternativas.
H 0: el modelo de regresión no explica la variación en y
H A: el modelo de regresión explica la variación en y
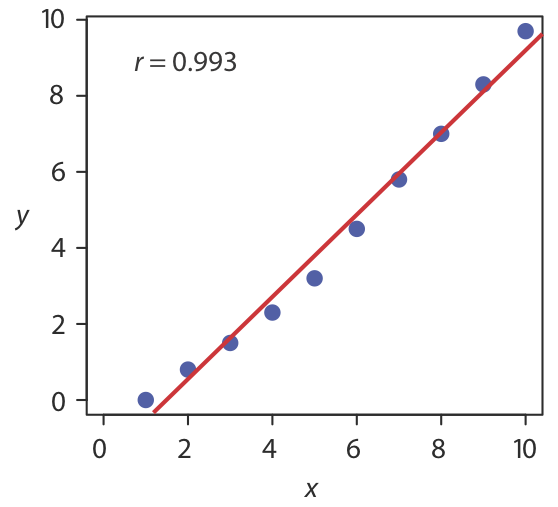
El valor en la columna para Significancia F es la probabilidad de retener la hipótesis nula. En este ejemplo, la probabilidad es\(2.5 \times 10^{-8}\), lo que es una fuerte evidencia para rechazar la hipótesis nula y aceptar el modelo de regresión. Como es el caso del coeficiente de correlación, un valor pequeño para la probabilidad es un resultado probable para cualquier curva de calibración, incluso cuando el modelo es inapropiado. La probabilidad de retener la hipótesis nula para los datos de la Figura\(\PageIndex{3}\), por ejemplo, es\(9.0 \times 10^{-5}\).
El coeficiente de correlación es una medida de la medida en que el modelo de regresión explica la variación en y. Los valores de r van de —1 a +1. Cuanto más cerca esté el coeficiente de correlación a +1 o a —1, mejor será el modelo para explicar los datos. Un coeficiente de correlación de 0 significa que no hay relación entre x e y. Al desarrollar los cálculos para regresión lineal, no se consideró el coeficiente de correlación. Hay una razón para ello. Para la mayoría de las curvas de calibración de línea recta el coeficiente de correlación es muy cercano a +1, típicamente 0.99 o mejor. Hay una tendencia, sin embargo, a poner demasiada fe en la significación del coeficiente de correlación, y a asumir que una r mayor a 0.99 significa que el modelo de regresión lineal es apropiado. La figura\(\PageIndex{3}\) proporciona un ejemplo de contraejemplo útil. Aunque la línea de regresión tiene un coeficiente de correlación de 0.993, los datos claramente son curvilíneos. La lección para llevar a casa es sencilla: ¡no te enamores del coeficiente de correlación!
Predecir la incertidumbre en\(x\) Given\(y\)
Aunque la instalación base de R no incluye un comando para predecir la incertidumbre en la variable independiente\(x\), dado un valor medido para la variable dependiente\(y\), el paquete ChemCal sí lo hace. Para utilizar este paquete es necesario instalarlo ingresando el siguiente comando.
install.packages (“ChemCal”)
Una vez instalado, lo que solo necesitas hacer una vez, puedes acceder a las funciones del paquete usando el comando library ().
biblioteca (ChemCal)
El comando para predecir la incertidumbre en C A es inverse.predict () y toma la siguiente forma para una regresión lineal no ponderada
inverse.predict (objeto, newdata, alfa = valor)
donde object es el objeto que contiene los resultados del modelo de regresión, new-data es un objeto que contiene uno o más valores replicados para la variable dependiente y el valor es el valor numérico para el nivel de significancia. Usemos este comando para completar el ejemplo de la curva de calibración de la Sección 8.1 en la que determinamos la concentración de analito en una muestra usando tres análisis replicados. Primero, creamos un objeto que contiene las mediciones replicadas de la señal
rep_signal = c (29.32, 29.16, 29.51)
y luego completamos el cómputo usando el siguiente comando
inverse.predict (calcurve, rep_signal, alfa = 0.05)
lo que arroja los resultados mostrados aquí
$ Predicción
[1] 0.2412597
$`Error estándar`
[1] 0.002363588
$Confianza
[1] 0.006562373
$`Límites de confianza`
[1] 0.2346974 0.2478221
La concentración del analito, C A, viene dada por el valor $Predicción, y su desviación estándar,\(s_{C_A}\), se muestra como $`Error estándar`. El valor de $Confianza es el intervalo de confianza,\(\pm t s_{C_A}\), para la concentración del analito, y $`Límites de Confianza` proporciona el límite inferior y el límite superior para el intervalo de confianza para C A.
Uso de R para una regresión lineal ponderada
El comando de R para una regresión lineal no ponderada también permite una regresión lineal ponderada si incluimos un argumento adicional, pesos, cuyo valor es un objeto que contiene los pesos.
lm (y ~ x, pesos = objeto)
Usemos este comando para completar el ejemplo de regresión lineal ponderada en la Sección 8.2 Primero, necesitamos crear un objeto que contenga los pesos, que en R son los recíprocos de las desviaciones estándar en y,\((s_{y_i})^{-2}\). Usando los datos del ejemplo anterior, ingresamos
syi = c (0.02, 0.02, 0.07, 0.13, 0.22, 0.33)
w =1/syi^2
para crear el objeto, w, que contiene los pesos. Los comandos
ponderado_calcurve = lm (señal ~ conc, pesos = w)
resumen (weighted_calcurve)
generar la siguiente salida.
Llamar a:
lm (fórmula = señal ~ conc, pesos = w)
Residuos ponderados:
1 2 3 4 5 6
-2.223 2.571 3.676 -7.129 -1.413 -2.864
Coeficientes:
Estimación Std. Error t valor Pr (>|t|)
(Intercepción) 0.04446 0.08542 0.52 0.63
conc 122.64111 0.93590 131.04 2.03e-08 ***
—
Signif. códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '' 1
Error estándar residual: 4.639 en 4 grados de libertad
R al cuadrado múltiple: 0.9998, R cuadrado ajustado: 0.9997
Estadístico F: 1.717e+04 sobre 1 y 4 DF, valor p: 2.034e-08
Cualquier diferencia entre los resultados aquí mostrados y los resultados de la Sección 8.2 son el resultado de errores de redondeo en nuestros cálculos anteriores.
Es posible que hayas notado que esta forma de definir pesos es diferente a la que se muestra en la Sección 8.2 Al derivar ecuaciones para una regresión lineal ponderada, puedes elegir normalizar la suma de los pesos para igualar el número de puntos, o puedes elegir no hacerlo —el algoritmo en R no normaliza los pesos.
Uso de R para una regresión curvilínea
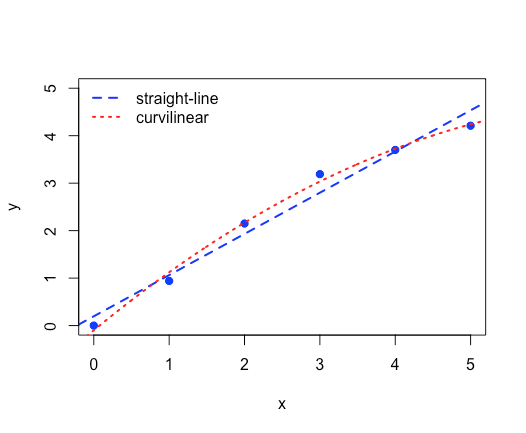
Como vemos en este ejemplo, podemos usar R para modelar datos que no están en forma de línea recta simplemente ajustando el modelo lineal.
Utilice los datos a continuación para explorar dos modelos para los datos de la siguiente tabla, uno usando una línea recta,\(y = \beta_0 + \beta_1 x\), y otro que es un polinomio de segundo orden,\(y = \beta_0 + \beta_1 x + \beta_2 x^2\).
| \(x_i\) | \(y_i\) |
|---|---|
| \ (x_i\) ">0.00 | \ (y_i\) ">0.00 |
| \ (x_i\) ">1.00 | \ (y_i\) ">0.94 |
| \ (x_i\) ">2.00 | \ (y_i\) ">2.15 |
| \ (x_i\) ">3.00 | \ (y_i\) ">3.19 |
| \ (x_i\) ">4.00 | \ (y_i\) ">3.70 |
| \ (x_i\) ">5.00 | \ (y_i\) ">4.21 |
Solución
Primero, creamos objetos para almacenar nuestros datos.
x = c (0, 1.00, 2.00, 3.00, 4.00, 5.00)
y = c (0, 0.94, 2.15, 3.19, 3.70, 4.21)
A continuación, construimos nuestros modelos lineales para una línea recta y para un ajuste curvilíneo a los datos
linea_recta = lm (y ~ x)
curvilíneo = lm (y ~ x + I (x^2))
y graficar los datos y ambos modelos lineales en la misma parcela. Debido a que abline () solo funciona para una línea recta, utilizamos nuestro modelo curvilíneo para calcular valores suficientes para x e y que podemos usar para trazar el modelo curvilíneo. Tenga en cuenta que los coeficientes para este modelo se almacenan en curvilinear$coeficientes siendo el primer valor\(\beta_0\)\(\beta_1\), siendo el segundo valor y siendo el tercer valor\(\beta_2\).
plot (x, y, pch = 19, col = “azul”, ylim = c (0,5), xlab = “x”, ylab = “y”)
abline (línea recta, lwd = 2, col = “azul”, lty = 2)
x_seq = seq (-0.5, 5.5, 0.01)
y_seq = curvilinear$coeficientes [1] + curvilinear$coeficientes [2] * x_seq + curvilinear$coeficientes [3] * x_seq^2
líneas (x_seq, y_seq, lwd = 2, col = “rojo”, lty = 3)
leyenda (x = “topleft”, legend = c (“línea recta”, “curvilínea”), col = c (“azul”, “rojo”), lty = c (2, 3), lwd = 2, bty = “n”)
Aquí se muestra la gráfica resultante.