9.3: Optimizaciones de un factor a la vez

Última actualización
Guardar como PDF

Page ID: 69256

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Un algoritmo simple para optimizar el método cuantitativo para vanadio descrito anteriormente es seleccionar concentraciones iniciales para H ₂ O ₂ y H ₂ SO ₄ y medir la absorbancia. A continuación, optimizamos un reactivo aumentando o disminuyendo su concentración, manteniendo constante la concentración del segundo reactivo, hasta que disminuya la absorbancia. Luego variamos la concentración del segundo reactivo, manteniendo la concentración óptima del primer reactivo, hasta que ya no vemos un aumento en la absorbancia. Podemos detener este proceso, al que llamamos optimización de un factor a la vez, después de un ciclo o repetir los pasos hasta que la absorbancia alcance un valor máximo o supere un valor umbral aceptable.

Una optimización de un factor a la vez es consistente con la noción de que para determinar la influencia de un factor debemos mantener constantes todos los demás factores. Este es un diseño experimental efectivo, aunque no necesariamente eficiente cuando los factores son independientes [ver Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986]. Dos factores son independientes cuando un cambio en el nivel de un factor no influye en el efecto de un cambio en el nivel del otro factor. Tabla\(\PageIndex{1}\) proporciona un ejemplo de dos factores independientes.

Mesa *\(\PageIndex{1}\)*. Ejemplo de dos factores independientes
factor A	factor B	respuesta
\(A_1\)	\(B_1\)	40
\(A_2\)	\(B_1\)	80
\(A_1\)	\(B_2\)	60
\(A_2\)	\(B_2\)	100

_{Si mantenemos el factor B en el nivel B ₁, cambiar el factor A del nivel A1 al nivel _A2 aumenta la respuesta de 40 a 80, o un cambio en la respuesta,\(\Delta R\) de}

\[R = 80 - 40 = 40 \nonumber\]

Si mantenemos el factor B en el nivel B ₂, encontramos que tenemos el mismo cambio de respuesta cuando el nivel de factor A cambia de _A1 a _A2.

\[R = 100 - 60 = 40 \nonumber\]

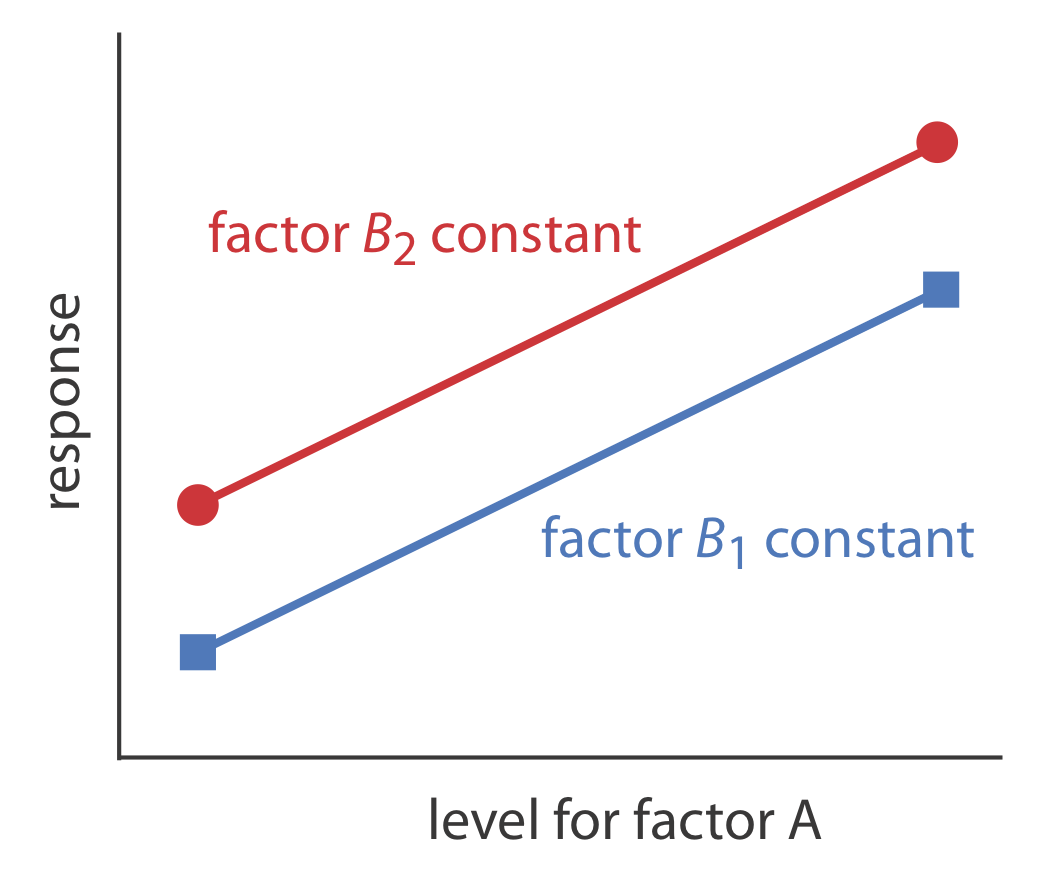
Podemos ver esta independencia visualmente si trazamos la respuesta en función del nivel del factor A' s, como se muestra en la Figura\(\PageIndex{1}\). Las líneas paralelas muestran que el nivel de factor B no influye en el efecto del factor A' s sobre la respuesta.

Figura14.6.png — Figura\(\PageIndex{1}\). Gráfica de efecto factorial para dos factores independientes. Tenga en cuenta que las dos líneas son paralelas, lo que indica que el nivel para el factor B no influye en cómo el nivel del factor A afecta la respuesta.

Matemáticamente, dos factores son independientes si no aparecen en el mismo término en la ecuación que describe la superficie de respuesta. La figura\(\PageIndex{2}\), por ejemplo, muestra la superficie pseudotridimensional resultante y un mapa de contorno para la ecuación

\[R = 2.0 + 0.12 A + 0.48 B - 0.03A^2 - 0.03 B^2 \nonumber \]

que describe una superficie de respuesta con factores independientes porque ningún término en la ecuación incluye tanto el factor A como el factor B.

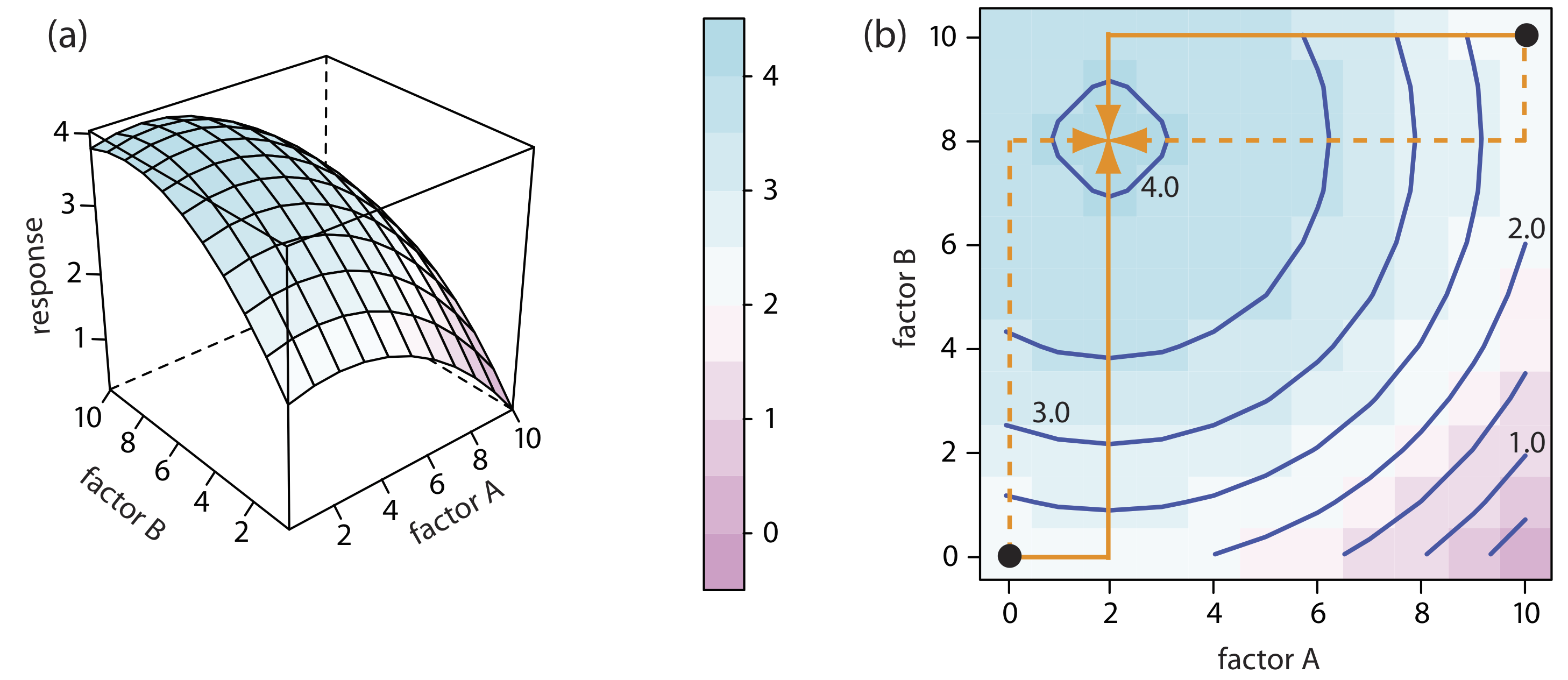
Figura14.7.png — Figura\(\PageIndex{2}\). La superficie de respuesta para dos factores independientes basada en la ecuación\(R = 2.0 + 0.12 A + 0.48 B - 0.03A^2 - 0.03 B^2\) y se muestra como (a) una estructura de alambre, y como (b) una gráfica de contorno superpuesta y una gráfica de nivel. Las líneas naranjas en (b) muestran el progreso de optimizaciones de un factor a la vez comenzando desde dos puntos de partida (•) y optimizando primero el factor A (línea continua) o el factor B primero (línea discontinua). Los cuatro ensayos alcanzan la respuesta óptima de (2,8) en un solo ciclo.

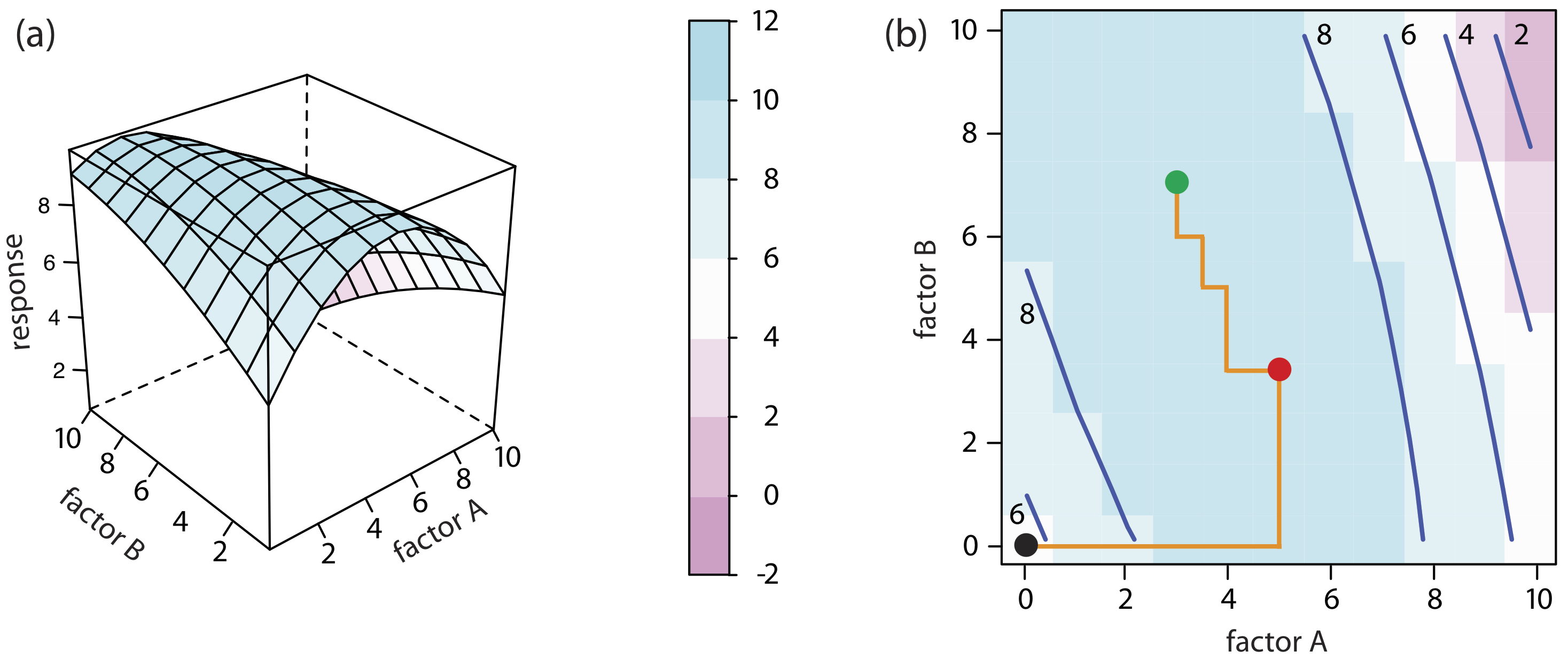
La forma más fácil de seguir el progreso de un algoritmo de búsqueda es mapear su ruta en una gráfica de contorno de la superficie de respuesta. Las posiciones en la superficie de respuesta se identifican como (a, b) donde a y b son los niveles para el factor A y para el factor B. La gráfica de contorno en la Figura\(\PageIndex{2b}\), por ejemplo, muestra cuatro optimizaciones de un factor a la vez de la superficie de respuesta en la Figura\(\PageIndex{2a}\). La efectividad y eficiencia de este algoritmo a la hora de optimizar factores independientes es clara: cada ensayo alcanza la respuesta óptima en (2, 8) en un solo ciclo.

Desafortunadamente, los factores a menudo no son independientes. Consideremos, por ejemplo, los datos de la Tabla\(\PageIndex{2}\)

Mesa *\(\PageIndex{2}\)*. Ejemplo de dos factores dependientes
factor A	factor B	respuesta
\(A_1\)	\(B_1\)	20
\(A_2\)	\(B_1\)	80
\(A_1\)	\(B_2\)	60
\(A_2\)	\(B_2\)	80

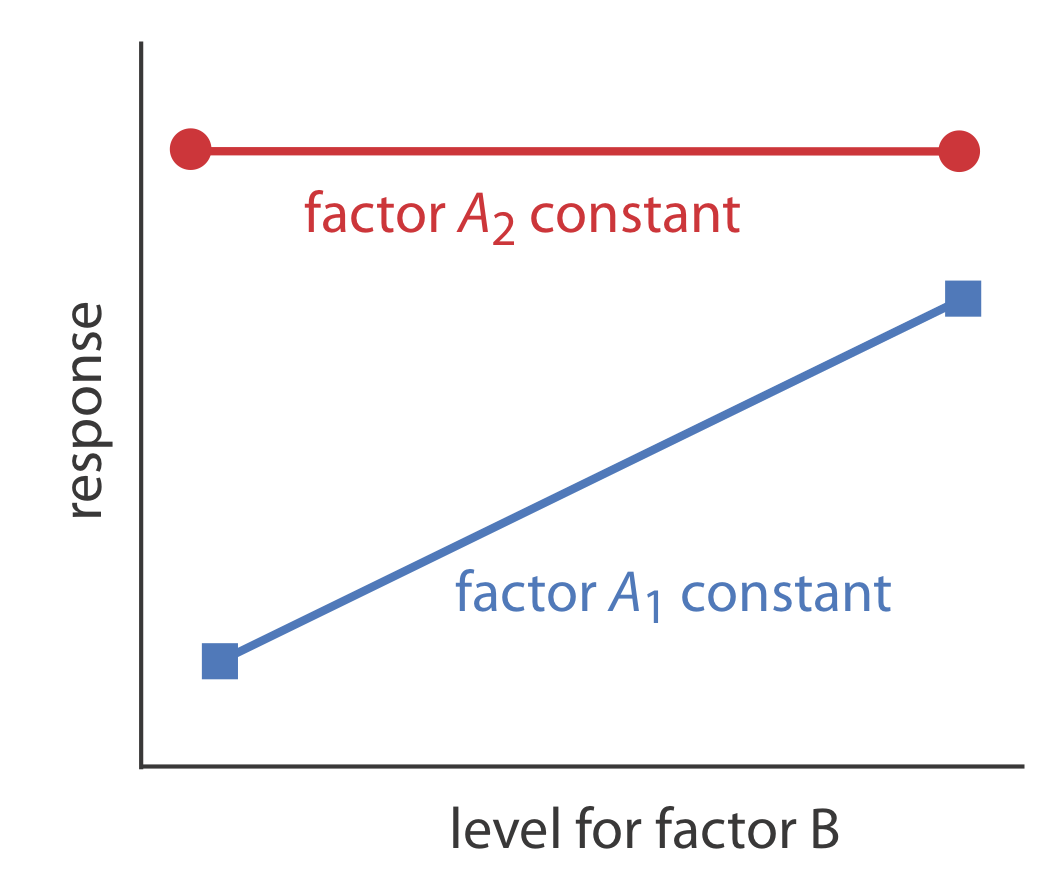
donde un cambio en el nivel de factor B del nivel B ₁ al nivel _B2 tiene un efecto significativo en la respuesta cuando el factor A está en el nivel _A1

\[R = 60 - 20 = 40 \nonumber\]

pero ningún efecto cuando el factor A está en el nivel A ₂.

\[R = 80 - 80 = 0 \nonumber\]La figura\(\PageIndex{3}\) muestra esta relación dependiente entre los dos factores.

Figura14.8.png — Figura\(\PageIndex{3}\). Gráfica de efecto factorial para dos factores dependientes. Tenga en cuenta que las dos líneas no son paralelas, lo que indica que el nivel para el factor A influye en cómo el nivel del factor B afecta la respuesta.

Se dice que los factores que son dependientes interactúan y la ecuación para la superficie de respuesta incluye un término de interacción que contiene tanto el factor A como el factor B. El término final en esta ecuación

\[R = 5.5 + 1.5 A + 0.6 B - 0.15 A^2 - 0.245 B^2 - 0.0857 AB \nonumber \]

por ejemplo, da cuenta de la interacción entre el factor A y el factor B. La figura\(\PageIndex{4}\) muestra la superficie pseudotridimensional resultante y un mapa de contorno para la superficie de respuesta definida por esta ecuación. El progreso de una optimización de un factor a la vez para esta superficie de respuesta se muestra en la Figura\(\PageIndex{4b}\). Aunque la optimización para factores dependientes es efectiva, es menos eficiente que para factores independientes. En este caso se necesitan cuatro ciclos para alcanzar la respuesta óptima de (3, 7) si comenzamos en (0, 0).

Figura14.9.png — Figura\(\PageIndex{4}\). La superficie de respuesta para dos factores dependientes basada en la ecuación\(R = 5.5 + 1.5 A + 0.6 B - 0.15 A^2 - 0.245 B^2 - 0.0857 AB\) y se muestra como (a) una estructura de alambre, y como (b) una gráfica de contorno superpuesta y una gráfica de nivel. *Las líneas naranjas en (b) muestran el progreso de la optimización de un factor a la vez comenzando desde el punto de inicio (•) y optimizando primero el factor A.* El punto rojo (•) marca el final del primer ciclo. Se necesitan cuatro ciclos para alcanzar la respuesta óptima de (3, 7) como lo muestra el punto verde (•).