9.4: Optimización Simplex
- Page ID
- 69271
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una estrategia para mejorar la eficiencia de un algoritmo de búsqueda es cambiar más de un factor a la vez. Una manera conveniente de lograr esto cuando hay dos factores es comenzar con tres conjuntos de niveles de factores iniciales dispuestos como los vértices de un triángulo (Figura\(\PageIndex{1}\). Después de medir la respuesta para cada conjunto de niveles de factores, identificamos la combinación que da la peor respuesta y la reemplazamos por un nuevo conjunto de niveles de factores usando un conjunto de reglas. Este proceso continúa hasta alcanzar el óptimo global o hasta que no sea posible una mayor optimización. El conjunto de niveles de factores se llama simplex. En general, para k factores un simplex es una figura geométrica\(k + 1\) dimensional [ver Spendley, W.; Hext, G. R.; Himsworth, F. R. Technometrics 1962, 4, 441—461, y Deming, S. N.; Parker, L. R. CRC Crit. Rev. Anal. Chem. 1978 7 (3), 187—202]. Así, para dos factores el simplex es un triángulo. Por tres factores el simplex es un tetraedro.
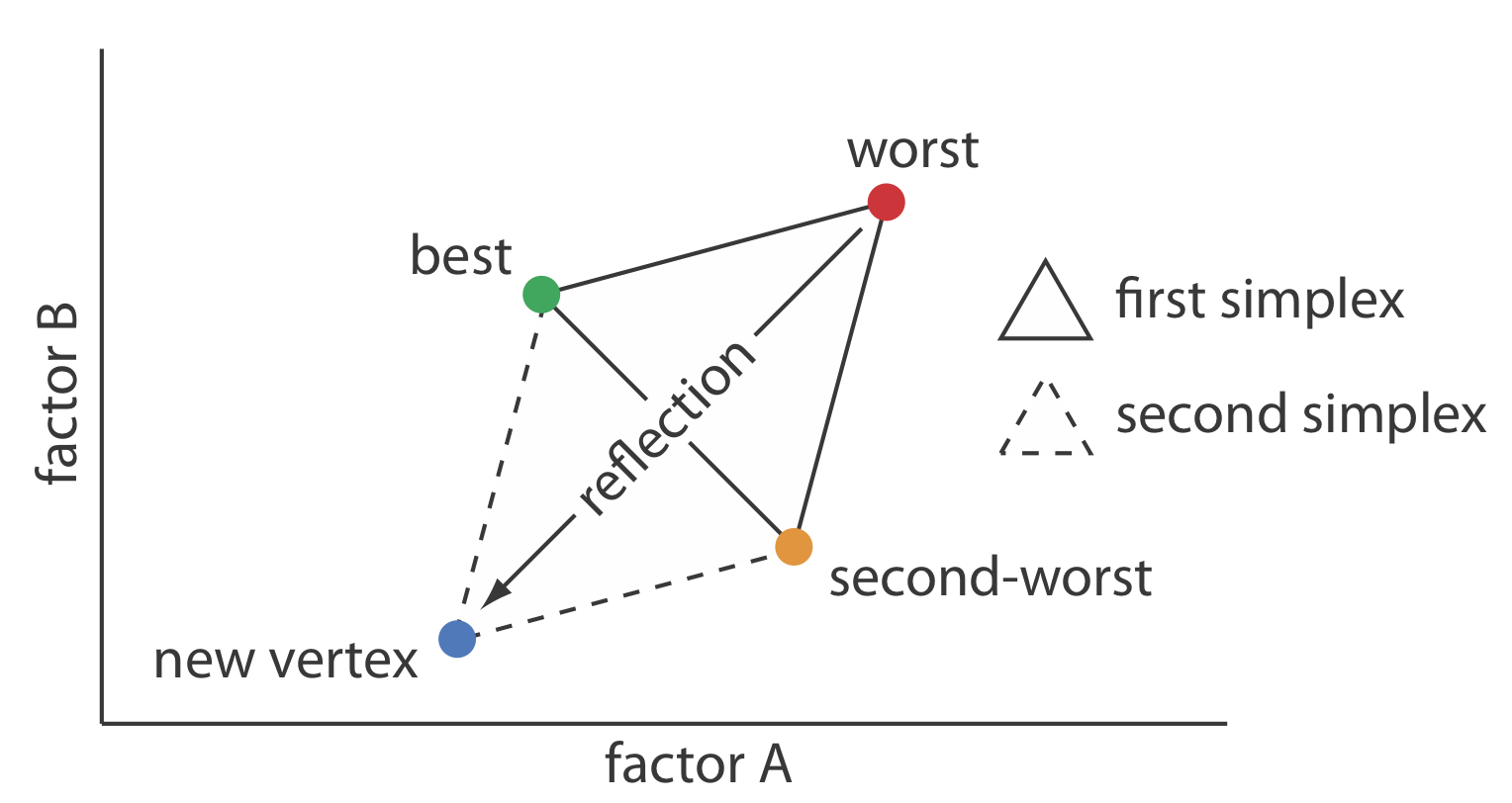
Para colocar el simplex inicial de dos factores en la superficie de respuesta, elegimos un punto de partida (a, b) para el primer vértice y colocamos los dos vértices restantes en (a + s a, b) y (a + 0. 5s a, b + 0. 87s b) donde s a y s b son tamaños de paso para el factor A y para el factor B [ver, por ejemplo, Largo, D. E. Anal. Chim. Acta 1969, 46, 193—206]. El siguiente conjunto de reglas mueve el simplex a través de la superficie de respuesta en busca de la respuesta óptima:
Regla 1. Clasificar los vértices de mejor (v b) a peor (v w).
Regla 2. Rechazar el peor vértice (v w) y reemplazarlo por un nuevo vértice (v n) reflejando el peor vértice a través del punto medio de los vértices restantes. Los niveles de factor del nuevo vértice son el doble de los niveles de factor promedio para los vértices retenidos menos los niveles de factor para el peor vértice. Para una optimización de dos factores, las ecuaciones se muestran aquí donde v s es el tercer vértice.
\[a_{v_n} = 2 \left( \frac {a_{v_b} + a_{v_s}} {2} \right) - a_{v_w} \nonumber \]
\[b_{v_n} = 2 \left( \frac {b_{v_b} + b_{v_s}} {2} \right) - b_{v_w} \nonumber \]
Regla 3. Si el nuevo vértice tiene la peor respuesta, entonces regresa al vértice anterior y rechaza el vértice con la segunda peor respuesta, (v s) calculando los niveles de factor del nuevo vértice usando la regla 2. Esta regla asegura que el simplex no regrese al simplex anterior.
Regla 4. Las condiciones de contorno son una forma útil de limitar el rango de posibles niveles de factores. Por ejemplo, puede ser necesario limitar la concentración de un factor por razones de solubilidad, o limitar la temperatura porque un reactivo es térmicamente inestable. Si el nuevo vértice excede una condición de límite, entonces asígnele la peor respuesta y siga la regla 3.
Debido a que el tamaño del simplex permanece constante durante la búsqueda, este algoritmo se denomina optimización simplex de tamaño fijo. El siguiente ejemplo ilustra la aplicación de estas reglas.
Encontrar el óptimo para la superficie de respuesta descrita por la ecuación
\[R = 5.5 + 1.5 A + 0.6 B - 0.15 A^2 - 0.254 B^2 - 0.0857 AB \nonumber \]
usando el algoritmo de búsqueda simplex de tamaño fijo. Use (0, 0) para los niveles de factor iniciales y establezca el tamaño de paso de cada factor en 1.00.
Solución
Dejando a = 0, b =0, s a = 1.00, y s b = 1.00 da los vértices para el simplex inicial como
\[\text{vertex 1:} (a, b) = (0, 0) \nonumber\]
\[\text{vertex 2:} (a + s_a, b) = (1.00, 0) \nonumber\]
\[\text{vertex 3:} (a + 0.5s_a, b + 0.87s_b) = (0.50, 0.87) \nonumber\]
Las respuestas para los tres vértices se muestran en la siguiente tabla
| vértice | a | b | respuesta |
|---|---|---|---|
| \(v_1\) | 0 | 0 | 5.50 |
| \(v_2\) | 1.00 | 0 | 6.85 |
| \(v_3\) | 0.50 | 0.87 | 6.68 |
con\(v_1\) dar la peor respuesta y\(v_3\) la mejor respuesta. Siguiendo la Regla 1, la rechazamos\(v_1\) y sustituimos por un nuevo vértice; así
\[a_{v_4} = 2 \left( \frac {1.00 + 0.50} {2} \right) - 0 = 1.50 \nonumber\]
\[b_{v_4} = 2 \left( \frac {0 + 0.87} {2} \right) - 0 = 0.87 \nonumber\]
La siguiente tabla da los vértices del segundo simplex.
| vértice | a | b | respuesta |
|---|---|---|---|
| \(v_2\) | 1.50 | 0 | 6.85 |
| \(v_3\) | 0.50 | 0.87 | 6.68 |
| \(v_4\) | 1.50 | 0.87 | 7.80 |
con\(v_3\) dar la peor respuesta y\(v_4\) la mejor respuesta. Siguiendo la Regla 1, la rechazamos\(v_3\) y sustituimos por un nuevo vértice; así
\[a_{v_5} = 2 \left( \frac {1.00 + 1.50} {2} \right) - 0.50 = 2.00 \nonumber\]
\[b_{v_5} = 2 \left( \frac {0 + 0.87} {2} \right) - 0.87 = 0 \nonumber\]
La siguiente tabla da los vértices del tercer simplex.
| vértice | a | b | respuesta |
|---|---|---|---|
| \(v_2\) | 1.50 | 0 | 6.85 |
| \(v_4\) | 1.50 | 0.87 | 780 |
| \(v_5\) | 2.00 | 0 | 7.90 |
El cálculo de los vértices restantes se deja como ejercicio. La figura\(\PageIndex{2}\) muestra el progreso de la optimización completa. Después de 29 pasos el simplex comienza a repetirse, dando vueltas alrededor de la respuesta óptima de (3, 7).
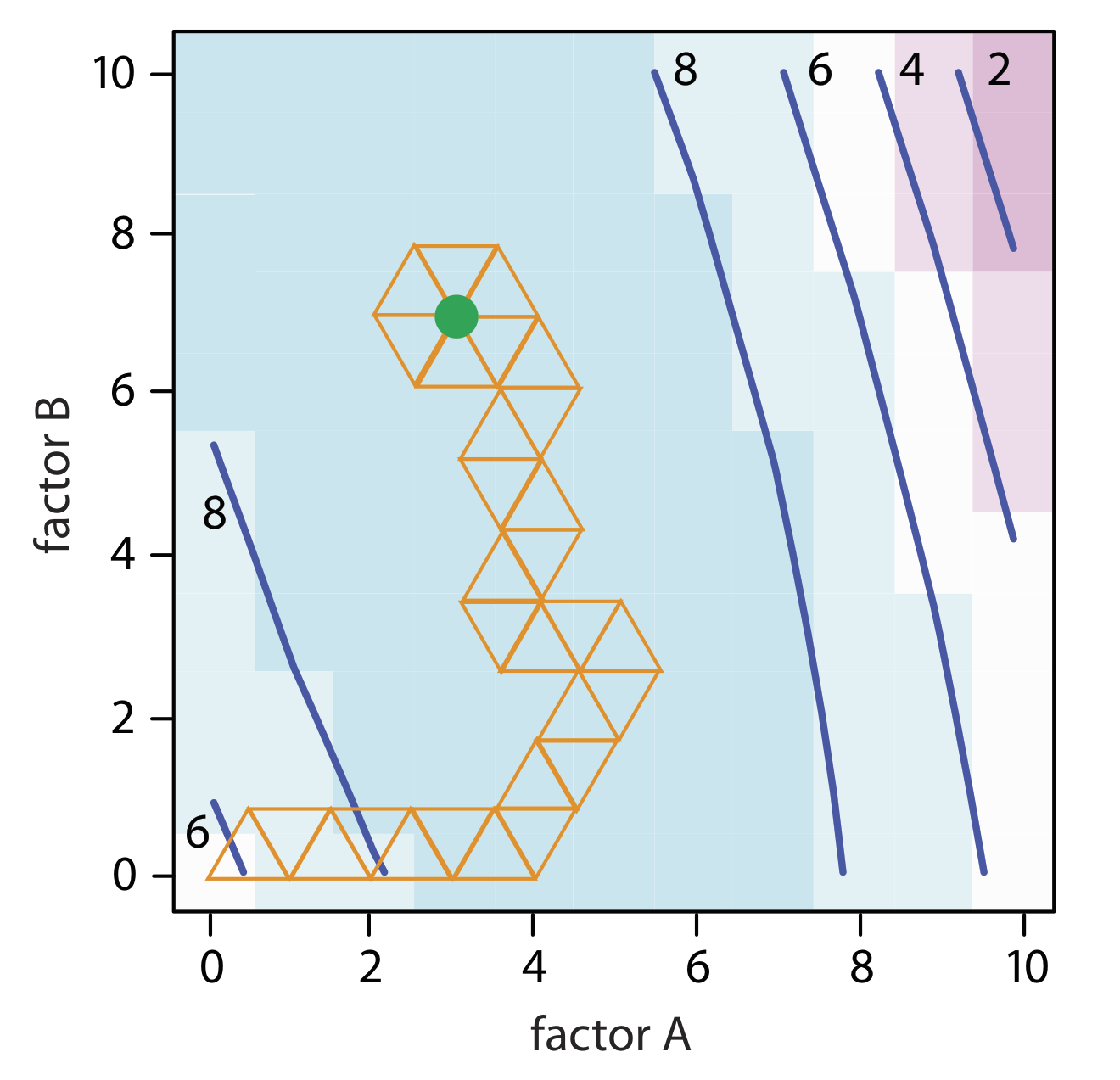
El tamaño del simplex inicial finalmente limita la efectividad y la eficiencia de un algoritmo de búsqueda simplex de tamaño fijo. Podemos aumentar su eficiencia permitiendo que el tamaño del simplex se expanda o contraiga en respuesta a la tasa a la que nos acercamos al óptimo. Por ejemplo, si encontramos que un nuevo vértice es mejor que cualquiera de los vértices en el simplex anterior, entonces expandimos el simplex más en esta dirección asumiendo que nos estamos moviendo directamente hacia el óptimo. Otras condiciones podrían hacer que contratemos lo simple, para hacerlo más pequeño, para fomentar la optimización para avanzar en una dirección diferente. Llamamos a esto una optimización simplex de tamaño variable. Consulte los recursos adicionales de este capítulo para obtener más detalles sobre la optimización simplex de tamaño variable.


