1.2: Polarización no lineal

Para la espectroscopia no lineal, calcularemos la polarización derivada de las interacciones con múltiples campos. Utilizaremos una expansión perturbadora\(P\) de poderes de los campos entrantes

\[\bar P(t)=P^{(0)}+P^{(1)}+P^{(2)}+\cdots\]

donde\(P^{(n)}\) se refiere a la polarización que surge de los campos de luz\(n\) incidente. Entonces,\(P^{(2)}\) y superiores son los términos no lineales. Calculamos P a partir de la matriz de densidad

\[\begin{align*} \bar P(t) &=Tr\left(\bar\mu_I(t)\rho_I(t)\right) \\[4pt] &=Tr\left(\bar\mu_I\rho_I^{(0)}\right)+Tr\left(\bar\mu_I\rho_I^{(1)}(t)\right)+Tr\left(\bar\mu_I\rho_I^{(2)}(t)\right)+\cdots \end{align*}\]

Como escribimos anteriormente,\(P_I^{(n)}\) es la expansión de ^orden n de la matriz de densidad

\[\rho^{(0)}=\rho_{eq}\nonumber\]

\[\rho^{(1)}=-\frac{i}{\hbar}\int\limits_{-\infty}^tdt_1\left[V_I(t_I),\rho_{eq}\right]\]

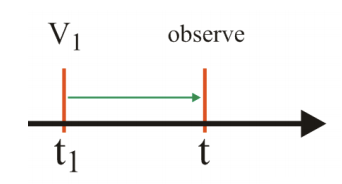
\[\rho^{(2)}=\left(-\frac{i}{\hbar}\right)^2\int\limits_{-\infty}^tdt_2\int\limits_{-\infty}^{t_2}dt_1\left[V_I(t_2)\left[V_I(t_I),\rho_{eq}\right]\right]\nonumber\]

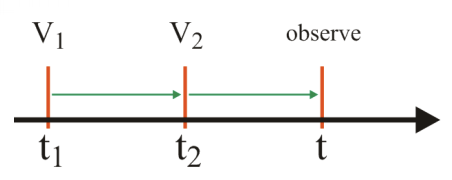
\[\rho_I^{(n)}=\left(-\frac{i}{\hbar}\right)^n\int\limits_{-\infty}^{t}dt_n\int\limits_{-\infty}^{t_n}dt_{n-1}\cdots\int\limits_{-\infty}^{t_2}dt_1\left[V_I(t_n),\left[V_I(t_{n-1}),\left[\cdots\left[V_I(t_1),\rho_{eq}\right]\cdots\right]\right]\right]\]

Examinemos la polarización de segundo orden para describir la función de respuesta no lineal. Anteriormente afirmamos que podríamos escribir la respuesta no lineal de segundo orden surgida de dos interacciones ordenadas por tiempo con potenciales externos en la forma

\[\bar P^{(2)}(t)=\int\limits_0^{\infty}d\tau_2\int\limits_0^{\infty}d\tau_1R^{(2)}\left(\tau_2,\tau_1\right)\bar E_1\left(t-\tau_2-\tau_1\right)\bar E_2\left(t-\tau_2\right)\]

Podemos comparar este resultado con lo que obtenemos de\(P^{(2)}(t)=Tr\left(\mu_I(t)\rho_I^{(2)}(t)\right)\). Sustituyendo como hicimos en el caso lineal,

\ [\ begin {alineado}
P^ {(2)} (t) &=\ nombreoperador {Tr}\ izquierda\ {\ mu_ {I} (t)\ izquierda (-\ frac {i} {\ hbar}\ derecha) ^ {2}\ int_ {-\ infty} ^ {t} d t_ {2}\ int_ {-\ infty} ^ {t_ 2}} d t_ {1}\ izquierda [V_ {I}\ izquierda (t_ {2}\ derecha),\ izquierda [V_ {I}\ izquierda (t_ {1}\ derecha),\ rho_ {e q}\ derecha]\ derecha]\ derecha\}\ derecha\}\
&=\ izquierda (\ frac {i} {\ hbar }\ derecha) ^ {2}\ int_ {-\ infty} ^ {t} d t_ {2}\ int_ {-\ infty} ^ {t_ {2}} d t_ {1} E_ {2}\ izquierda (t_ {2}\ derecha) E_ {1}\ izquierda (t_ {1}\ derecha)\ nombre del operador {Tr}\ izquierda\\ izquierda [\ izquierda [\ mu_ {I} (t),\ mu_ {I}\ izquierda (t_ {2}\ derecha)\ derecha],\ mu_ {I}\ izquierda (t_ {1}\ derecha)\ derecha]\ rho_ {e q}\ derecha\}\ derecha\}\
&=\ izquierda (\ frac {i} {\ hbar}\ derecha) ^ {2}\ int _ {0} ^ {\ infty} d\ tau_ {2}\ int_ {0} ^ {\ infty} d\ tau_ {1} E_ {2}\ izquierda (t-\ tau_ {2}\ derecha) E_ {1}\ izquierda (t-\ tau_ {2} -\ tau_ {1}\ derecha)\ nombreoperador {Tr}\ izquierda\ {izquierda\ [\ izquierda [\ mu_ {I}\ izquierda (\ tau_ {1} +\ tau_ {2}\ derecha),\ mu_ {I}\ izquierda (\ tau_ {1}\ derecha)\ derecha],\ mu_ {I} (0)\ derecha]\ rho_ {e q}\ derecha\}
\ final {alineada}\ etiqueta {2.2.5}\ ]

En la última línea cambiamos las variables a los intervalos de tiempo\(t_1=t-\tau_1-\tau_2\) y\(t_2=t-\tau_2\), e hicimos cumplir el orden de tiempo\(t_1 \le t_2\). La comparación de las ecuaciones (2.2.4) y (2.2.5) nos permite afirmar que la función de respuesta no lineal de segundo orden es

\[ R^{(2)}\left(\tau_{1}, \tau_{2}\right)=\left(\frac{i}{\hbar}\right)^{2} \theta\left(\tau_{1}\right) \theta\left(\tau_{2}\right) \operatorname{Tr}\left\{\left[\left[\mu_{I}\left(\tau_{1}+\tau_{2}\right), \mu_{I}\left(\tau_{1}\right)\right], \mu_{I}(0)\right] \rho_{e q}\right\} \label{2.2.6} \]

Nuevamente, para interacciones impulsivas (es decir, pulsos de luz de función delta), la polarización no lineal es directamente proporcional a la función de respuesta. Ejercicios similares a la respuesta lineal y de segundo orden se pueden usar para mostrar que la función de respuesta no lineal a orden arbitrario\(R^{(n)}\) es

\ [\ begin {alineada}
R^ {(n)}\ izquierda (\ tau_ {1},\ tau_ {2},\ ldots\ tau_ {n}\ derecha) &=\ izquierda (\ frac {i} {\ hbar}\ derecha) ^ {n}\ theta\ izquierda (\ tau_ {1}\ derecha)\ theta\ izquierda (\ tau_ {2} derecha)\ lpuntos\ theta\ izquierda (\ tau_ {n}\ derecha)\\
&\ veces\ nombreoperador {Tr}\ izquierda\ {\ izquierda [\ izquierda [\ ldots\ izquierda [\ mu_ {I}\ izquierda (\ tau_ {n} +\ tau_ {n-1} +\ ldots+\ tau_ {1}\ derecha),\ mu_ {I}\ izquierda (\ tau_ {n-1} +\ tau_ {n} +\ cdots\ tau_ {1}\ derecha)\ derecha],\ ldots\ derecha]\ mu_ {I} (0)\ derecha]\ rho_ {e q}\ derecho\}
\ final {alineado}\ etiqueta {2.2.7}\]

Vemos que en general las funciones de respuesta no lineal son sumas de funciones de correlación, y la respuesta de ^orden n tiene 2n funciones de correlación que contribuyen. Estas funciones de correlación difieren según si los operadores secuenciales actúan en el lado del sujetador o ket de ρ al hacer cumplir el orden de tiempo. Dado que los lados de sujetador y ket representan funciones de onda conjugadas, estas funciones de correlación contendrán coherencias con diferentes relaciones de fase durante intervalos de tiempo posteriores.

Para ver más específicamente a qué se refiere un término específico en estos conmutadores anidados, veamos\(R^{(2)}\) y hagamos cumplir el orden del tiempo:

Término 1 en eq. (2.2.7)

\[\begin{aligned} Q_1 &= Tr\left(\mu_1(\tau_1+\tau_2)\mu_I(\tau_1)\mu_I(0)\rho_{eq}\right) \\ &= Tr\left(\frac{U_0^{\dagger}(\tau_1+\tau_2)}{U_0^{\dagger}(\tau_1)U_0^{\dagger}(\tau_2)}\mu\frac{U_0(\tau_1+\tau_2)U_0^{\dagger}(\tau)}{U_0(\tau_2)}\mu U_0(\tau_1)\mu\rho_{eq}\right) \\ &=Tr\left(\mu U_0(\tau_2)\mu U_0(\tau_1)\mu\rho_{eq}U_0^{\dagger}(\tau_1)U_0^{\dagger}(\tau_2)\right) \end{aligned} \]

(1) dipolo actúa sobre ket de\(\rho_{eq}\)

(2) evolucionar bajo\(H_0\) durante\(\tau_1\).

(3) el dipolo actúa sobre ket.

(4) Evolucionar durante\(\tau_2\).

(5) Multiplicar por\(\mu\) y tomar rastro.

Interacción KET/KET

En cada punto de interacción con el potencial externo, el operador dipolo actuó en el lado ket de ρ. Las diferentes funciones de correlación se distinguen por el orden en que actúan sobre sujetador o ket. Solo contamos las interacciones con los campos del incidente, y la convención es que el operador final que usamos antes del rastreo actúa en el lado ket. Entonces el término Q ₁ es una interacción ket/ket. Una forma alternativa de expresar esta función de correlación es en términos del propagador de tiempo para la matriz de densidad, un superoperador definido a través de:\(\hat G(t)\rho_{ab}=U_0|a\rangle\langle b|U_0^{\dagger}\). Recordando el orden del tiempo, esto permite que Q ₁ se escriba como

\[Q_1 = Tr\left(\mu\hat G(\tau_2)\mu\hat G(\tau_1)\mu\rho_{eq}\right) \label{2.2.8}\]

Término 2

\[\begin{aligned} Q_2 &=Tr\left(\mu_I(0)\mu_I(\tau_1+\tau_2)\mu_I(\tau_1)\rho_{eq}\right) \\ &=Tr\left(\mu_I(\tau_1+\tau_2)\mu_I(\tau_1)\rho_{eq}\mu_I(0)\right) \end{aligned}\nonumber\]

Interacción BRA/KET

Para los términos restantes observamos que la interacción del lado del sujetador es el complejo conjugado del lado ket, por lo que de los cuatro términos en la ecuación (2.2.7), podemos identificar solo dos términos independientes:

\[Q_1 \Rightarrow ket/ket ~~~~~ Q_1^* \Rightarrow bra/bra ~~~~~ Q_2 \Rightarrow ket/bra ~~~~~ Q_2^* \Rightarrow bra/ket \nonumber\]

Esta es una observación general. Para\(R^{(n)}\), realmente solo necesitas calcular 2 funciones de correlación ^n-1. Entonces para\(R^{(2)}\) escribimos

\[R^{(2)}=\left(\frac{i}{\hbar}\right)^{2} \theta\left(\tau_{1}\right) \theta\left(\tau_{2}\right) \sum_{\alpha=1}^{2}\left[Q_{\alpha}\left(\tau_{1}, \tau_{2}\right)-Q_{\alpha}^{*}\left(\tau_{1}, \tau_{2}\right)\right] \label{2.2.9}\]

donde

\[Q_1=Tr\left[\mu_I(\tau_1+\tau_2)\mu_I(\tau_1)\mu_I(0)\rho_{eq}\right] \label{2.2.10}\]

\[Q_1=Tr\left[\mu_I(\tau_1)\mu_I(\tau_1+\tau_2)\mu_I(0)\rho_{eq}\right] \label{2.2.11}\]

Entonces, ¿cuál es la diferencia en estas funciones de correlación? Una vez que hay más de un campo de excitación, y más de un periodo de tiempo durante el cual las coherencias pueden evolucionar, entonces se debe comenzar a observar cuidadosamente la fase relativa que adquieren las coherencias durante diferentes periodos de tiempo consecutivos,\(\phi(\tau)=\omega_{ab}\tau\). Para ilustrar, considere la evolución del paquete de ondas: la interacción de la luz puede impartir un impulso positivo o negativo (\(\pm\bar k_{in}\)) a la evolución del paquete de ondas, lo que influye en la dirección de propagación y la fase de movimiento en relación con otros estados. Cualquier campo posterior que actúe sobre este estado debe tener en cuenta la superposición dependiente del tiempo de estos grupos de ondas con otros estados objetivo. Los diferentes términos en la función de respuesta no lineal explican todas las permutaciones de interacciones y la fase adquirida por estas coherencias involucradas. La suma describe la evolución incluyendo posibles efectos de interferencia entre diferentes vías de interacción.