2.3: Ejemplo de respuesta lineal para un sistema de dos niveles

Última actualización
Guardar como PDF

Page ID: 73743

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Consideremos el enfoque diagramático del problema de absorción lineal, utilizando un sistema de dos niveles con un nivel inferior\(a\) y un nivel superior\(b\). Solo hay una función de correlación independiente en la función de respuesta lineal

\[\begin{aligned} C(t) &= Tr[\mu(t)\mu(0)\rho_{eq}] \\[4pt] &=Tr[\mu\hat G(t)\mu\rho_{eq}]\end{aligned}\label{3.3.1}\]

Esto no necesita conocerse antes de comenzar, pero es útil a considerar, ya que al final se debe recuperar. El sistema se llevará a iniciar en el estado base\(\rho_{aa}\). La respuesta lineal solo permite una interacción de campo de entrada, que debe ser absorción, y que tomamos como una interacción lateral ket. Ahora podemos dibujar dos diagramas:

Con este diagrama, podemos comenzar describiendo las características de la señal en términos de la polarización inducida. El producto de los campos de incidencia indica:

\[E_1e^{-i\omega_1t+i\bar k_1\cdot\bar r} \Rightarrow P(t)e^{-i\omega_{sig}t+i\bar k_{sig}\cdot\bar r}\label{3.3.2}\]

para que

\[\omega_{sig}=\omega_1 ~~~~~ \bar k_{sig}=\bar k_1 \label{3.3.3}\]

Como era de esperar la señal irradiará con la misma frecuencia y en la misma dirección que el haz entrante. A continuación podemos anotar la función de correlación para este término. Trabajando de abajo hacia arriba:

(1) (2) (3) (4)

\ [\ begin {alineado} C (t) &=p_ {a}\ izquierda [\ mu_ {b a}\ derecha]\ izquierda [e^ {-i\ omega_ {b a} t-\ Gamma_ {b a} t}\ derecha]\ izquierda [\ mu_ {a b}\ derecha]\\
&=p_ {a}\ izquierda|\ mu_ {b a}\ derecha|^ {2} e^ {-i\ omega_ {b a} t-\ Gamma_ {b a} t}\ final {alineado}\ etiqueta {3.3.4}\]

Formas más sofisticadas de tratar la evolución del tiempo bajo\(H_0\) el paso (3) podrían tomar la forma de algunos de nuestros tratamientos anteriores de la forma de línea de absorción:

\[\begin{aligned}\hat{G}(\tau) \rho_{a b} & \sim \rho_{a b} \exp \left[-i \omega_{a b} \tau\right] F(\tau) \\&=\rho_{a b} \exp \left[-i \omega_{a b} \tau-g(t)\right] \end{aligned} \label{3.3.5}\]

Obsérvese que se podrían dibujar cuatro posibles permutaciones del diagrama lineal al considerar las interacciones del lado del sujetador y el ket, y la población inicial en los estados a y b:

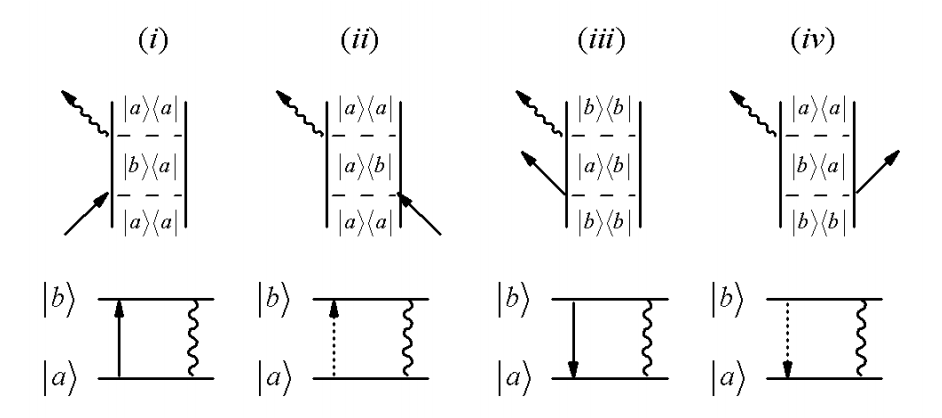
Sin embargo, no hay nuevo contenido dinámico en estos diagramas adicionales, y generalmente se toman para ser entendidos a través de un diagrama. El diagrama ii es solo el complejo conjugado de la ecuación (3.3.4) así que sumar esta contribución de señal da:

\[C(t)-C^*(t)=2ip_a|\mu_{ba}|^2\sin (\omega_{ba}t)e^{-\Gamma_{ba}t} \label{3.3.6}\]

Contabilizar la población térmicamente excitada inicialmente en b conduce a la función esperada de respuesta del sistema de dos niveles que depende de la diferencia poblacional

\[R(t)=\frac{2}{\hbar}(p_a-p_b)|\mu_{ba}|^2\sin (\omega_{ba}t)e^{-\Gamma_{ba}t} \label{3.3.7}\]