8.2: Las Ondas

Las soluciones a la ecuación de Schrödinger del átomo de hidrógeno son funciones que son productos de una función armónica esférica y una función radial.

\[ \psi _{n, l, m_l } (r, \theta , \varphi) = R_{n,l} (r) Y^{m_l}_l (\theta , \varphi) \label {8-20}\]

Las funciones de onda para el átomo de hidrógeno dependen de las tres variables r,\(\theta\), y\(\varphi \) y los tres números cuánticos n,\(l\), y\(m_l\). Las variables dan la posición del electrón con respecto al protón en coordenadas esféricas. El cuadrado absoluto de la función de onda,, evaluado en\(| \psi (r, \theta , \varphi )|^2\),\(r\)\(\theta \), y\(\varphi\) da la densidad de probabilidad de encontrar el electrón dentro de un volumen diferencial\(d \tau\), centrado en la posición especificada por r,\(\theta \), y\(\varphi\).

Ejercicio\(\PageIndex{1}\)

Cuál es el valor de la integral

\[ \int \limits _{\text{all space}} | \psi (r, \theta , \varphi )|^2 d \tau \, ? \nonumber\]

Los números cuánticos tienen nombres:\(n\) se llama el número cuántico principal,\(l\) se llama el número cuántico de momento angular, y\(m_l\) se llama el número cuántico magnético porque (como veremos en la Sección 8.4) la energía en un campo magnético depende de\(m_l\). A menudo\(l\) se le llama el número cuántico azimutal porque es una consecuencia\(\theta\) de la ecuación, que involucra el ángulo azimutal\(\Theta \), refiriéndose al ángulo al cenit.

Estos números cuánticos tienen valores específicos que están dictados por las restricciones físicas o condiciones de límite impuestas a la ecuación de Schrödinger:\(n\) debe ser un entero mayor que 0,\(l\) puede tener los valores de 0 a n‑1, y\(m_l\) puede tener\(2l + 1\) valores que van desde\(-l\) ‑ hasta \(+l\)en pasos unitarios o enteros. Los valores del número cuántico\(l\) suelen estar codificados por una letra: s significa 0, p significa 1, d significa 2, f significa 3; los siguientes códigos continúan alfabéticamente (por ejemplo, g significa\(l = 4\)). Los números cuánticos especifican la cuantificación de cantidades físicas. Las energías discretas de los diferentes estados del átomo de hidrógeno vienen dadas por\(n\), la magnitud del momento angular viene dada por\(l\), y un componente del momento angular (generalmente elegido por los químicos para ser el componente z) viene dado por\(m_l\). El número total de orbitales con un valor particular de\(n\) es\(n^2\).

Ejercicio\(\PageIndex{2}\)

Considerar varios valores para n, y mostrar que el número de orbitales para cada n es\(n^2\).

Ejercicio\(\PageIndex{3}\)

Construir una tabla que resuma los valores permitidos para los números cuánticos n,\(l\), y\(m_l\). para los niveles de energía 1 a 7 de hidrógeno.

Ejercicio\(\PageIndex{4}\)

La notación 3d especifica los números cuánticos para un electrón en el átomo de hidrógeno. ¿Cuáles son los valores para n y\(l\)? ¿Cuáles son los valores para la energía y el momento angular? ¿Cuáles son los valores posibles para el número cuántico magnético? ¿Cuáles son las posibles orientaciones para el vector de momento angular?

Las funciones de onda del átomo de hidrógeno,\(\psi (r, \theta , \varphi )\), se llaman orbitales atómicos. Un orbital atómico es una función que describe un electrón en un átomo. La función de onda con n = 1,\(l=1\), y\(m_l\) = 0 se llama orbital 1s, y un electrón que es descrito por esta función se dice que está “en” el orbital ls, es decir, tiene un estado orbital 1s. Las restricciones sobre\(n\),\(l)\), y\(m_l\) que se imponen durante la solución del átomo de hidrógeno ecuación de Schrödinger explican por qué hay un solo orbital 1s, por qué hay tres orbitales 2p, cinco orbitales 3d, etc. Veremos cuando consideremos los átomos multielectrón en el Capítulo 9 que estas restricciones explican las características de la Tabla Periódica. En otras palabras, la Tabla Periódica es una manifestación del modelo de Schrödinger y las restricciones físicas impuestas para obtener las soluciones a la ecuación de Schrödinger para el átomo de hidrógeno.

Visualizar la variación de una función de onda electrónica con\(r\)\(\theta\), y\(\varphi\) es importante porque el cuadrado absoluto de la función de onda representa la distribución de carga (densidad de probabilidad de electrones) en un átomo o molécula. La distribución de carga es fundamental para la química porque está relacionada con la reactividad química. Por ejemplo, una parte deficiente en electrones de una molécula es atraída por una región rica en electrones de otra molécula, y tales interacciones juegan un papel importante en interacciones químicas que van desde reacciones de sustitución y adición hasta plegamiento de proteínas y la interacción de sustratos con enzimas.

Visualizar las funciones de onda y las distribuciones de carga es un desafío porque requiere examinar el comportamiento de una función de tres variables en el espacio tridimensional. Esta visualización se facilita al considerar las partes radial y angular por separado, pero trazar las partes radial y angular por separado no revela muy bien la forma de un orbital. La forma se puede revelar mejor en una gráfica de densidad de probabilidad. Para hacer tal trama tridimensional, divida el espacio en elementos de pequeño volumen, calcule\(\psi^* \psi \) en el centro de cada elemento de volumen, y luego sombree, puntee o coloree ese elemento de volumen en proporción a la magnitud de\(\psi^* \psi \). No confunda tales parcelas con parcelas polares, que se ven similares.

Las densidades de probabilidad también pueden ser representadas por mapas de contorno, como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Gráficas de contorno en el plano\(2p_x\) x-y para los\(3p_x\) orbitales y del átomo de hidrógeno. Las parcelas mapean líneas de valores constantes de\(R(r)^2\); líneas rojas siguen caminos de alto\(R(r)^2\), azul para bajo\(R(r)^^2\). La función angular utilizada para crear la figura fue una combinación lineal de dos funciones armónicas esféricas (ver Problema 10 al final de este capítulo).

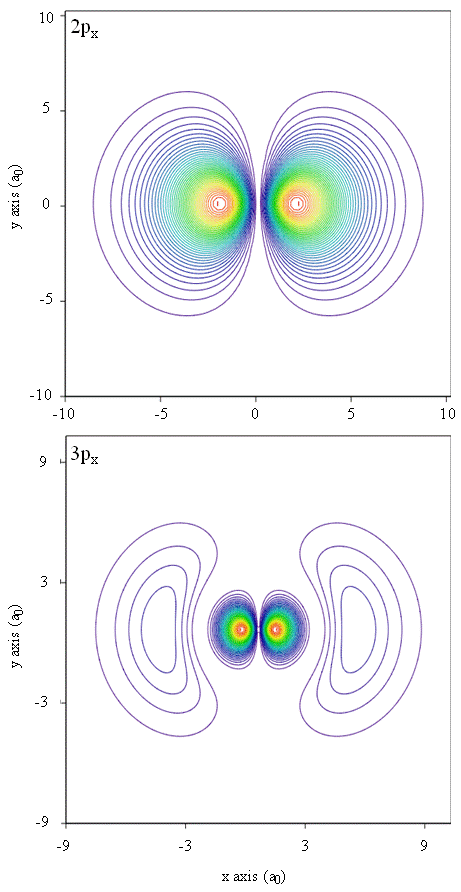
Otra técnica de representación, el modelado de realidad virtual, es muy prometedora para la representación de las densidades de electrones. Imagina, por ejemplo, poder experimentar la densidad de electrones como una fuerza o resistencia sobre una varita que se mueve a través del espacio tridimensional. Dispositivos como estos, llamados dispositivos hápticos, ya existen y se están utilizando para representar información científica. Del mismo modo, ¿no sería interesante “volar” a través de un orbital atómico y experimentar cambios en la densidad de electrones como cambios de color o cambios de nubosidad? Actualmente se están desarrollando salas especialmente diseñadas con pantallas 3D y gafas “inteligentes” que brindan retroalimentación sobre la dirección de la mirada del espectador para permitirnos experimentar tales sensaciones.

Los métodos para examinar separadamente las porciones radiales de los orbitales atómicos proporcionan información útil sobre la distribución de la densidad de carga dentro de los orbitales. Gráficas de las funciones radiales\(R(r)\), para los orbitales 1s, 2s y 2p trazados en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Función radial, R (r), para los orbitales 1s, 2s y 2p.

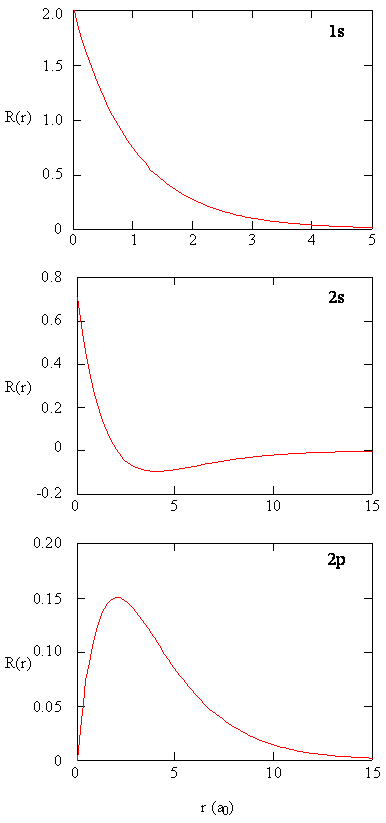
La función 1s en la Figura\(\PageIndex{2}\) comienza con un alto valor positivo en el núcleo y decae exponencialmente a esencialmente cero después de 5 radios Bohr. El alto valor en el núcleo puede ser sorprendente, pero como veremos más adelante, la probabilidad de encontrar un electrón en el núcleo es muy pequeña.

Siguiente Observe cómo la función radial para el orbital 2s, Figura\(\PageIndex{2}\), va a cero y se vuelve negativa. Este comportamiento revela la presencia de un nodo radial en la función. Un nodo radial ocurre cuando la función radial es igual a cero que no sea at\(r = 0\) o\(r = ∞\). Los nodos y los comportamientos limitantes de las funciones orbitales atómicas son útiles para identificar qué orbital se está describiendo por qué función de onda. Por ejemplo, todas las funciones s tienen valores de función de onda distintos de cero en\(r = 0\), pero p, d, f y todas las demás funciones van a cero en el origen. Es útil recordar que hay nodos\(n-1-l\) radiales en una función de onda, lo que significa que un orbital 1s no tiene nodos radiales, un 2s tiene un nodo radial, y así sucesivamente.

Ejercicio\(\PageIndex{5}\)

Examinar las formas matemáticas de las funciones de onda radiales. ¿Qué característica de las funciones hace que algunas de ellas pasen a cero en el origen mientras que las funciones s no van a cero en el origen?

Ejercicio\(\PageIndex{6}\)

¿Qué característica matemática de cada una de las funciones radiales controla el número de nodos radiales?

Ejercicio\(\PageIndex{7}\)

¿A qué valor de r ocurre el nodo radial 2s?

Ejercicio\(\PageIndex{8}\)

Haga una tabla que proporcione la energía, el número de nodos radiales y el número de nodos angulares y el número total de nodos para cada función con n = 1, 2 y 3. Identificar la relación entre la energía y el número de nodos. Identificar la relación entre el número de nodos radiales y el número de nodos angulares.

La cantidad\(R (r) ^* R(r)\) da la densidad de probabilidad radial; es decir, la densidad de probabilidad para que el electrón esté en un punto ubicado a la\(r\) distancia del protón. Las densidades de probabilidad radial para tres tipos de orbitales atómicos se trazan en la Figura (\ PageIndex {3}\).

Figura\(\PageIndex{3}\): Densidades de probabilidad radiales para los orbitales 1s, 2s y 2p.

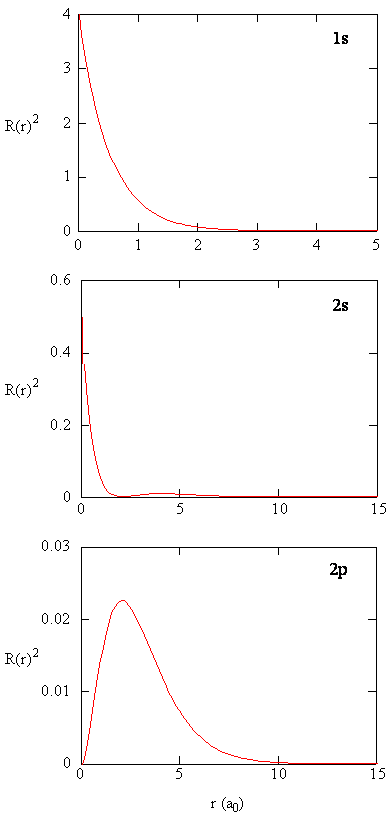
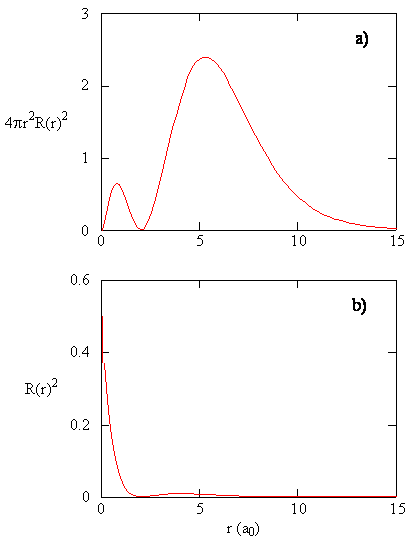
Cuando la densidad de probabilidad radial para cada valor de r se multiplica por el área de la superficie esférica representada por ese valor particular de r, obtenemos la función de distribución radial. La función de distribución radial da la densidad de probabilidad para que un electrón se encuentre en cualquier parte de la superficie de una esfera ubicada a una distancia r del protón. Dado que el área de una superficie esférica es\(4 \pi r^2\), la función de distribución radial viene dada por\(4 \pi r^2 R(r) ^* R(r)\).

Las funciones de distribución radial se muestran en la Figura\(\PageIndex{4}\). A valores pequeños de r, la función de distribución radial es baja porque la pequeña superficie para radios pequeños modula el valor alto de la función de densidad de probabilidad radial cerca del núcleo. A medida que aumentamos\(r\), la superficie asociada a un valor dado de r aumenta, y el\(r^2\) término hace que la función de distribución radial aumente aunque la densidad de probabilidad radial esté comenzando a disminuir. A grandes valores de\(r\), la decadencia exponencial de la función radial supera el aumento causado por el\(r^2\) término y la función de distribución radial disminuye.

Figura\(\PageIndex{4}\): La función de distribución radial para los orbitales 1s, 2s y 2p.

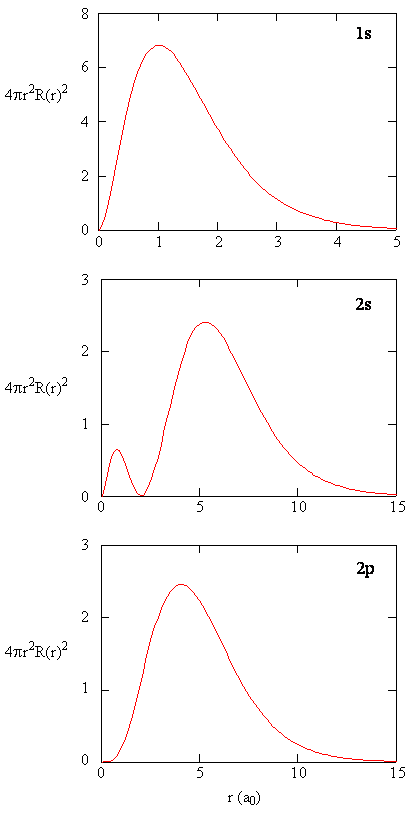
Ejercicio\(\PageIndex{9}\)

Escriba una comparación de calidad de la función radial y la función de distribución radial para el orbital 2s. Ver Figura (\ PageIndex {5}\)

Figura\(\PageIndex{5}\): Comparación de a) la función de distribución radial y b) la densidad de probabilidad radial para el orbital 2s.