8.8: Acoplamiento de Símbolos de Momento Angular y Término Espectroscópico
- Page ID
- 71317
Alrededor de 1930 varios espectroscopistas que utilizan instrumentos de alta resolución encontraron que las líneas en el espectro de átomos de hidrógeno en realidad no son líneas simples sino que son multipletes como se muestra para una mezcla isotópica de hidrógeno,\((H^1_{\alpha})\) y deuterio, (\(H^2_{\alpha}\)) en la Figura\(\PageIndex{1}\). Un multiplete consiste en dos o más líneas estrechamente espaciadas. Dos líneas juntas forman un doblete, tres un triplete, etc. Los multipletes también se denominan estructura fina. El término estructura fina significa que las líneas están espaciadas entre sí, es decir, finamente espaciadas. Dicha estructura fina también se encontró en espectros de iones de un electrón como He +.

Cabe recordar que la\(H^1_{\alpha}\) línea de la serie Balmer a 656.279 nm se entendió como resultado de una sola transición de un electrón desde el nivel de energía n = 3 al nivel n = 2. La observación de la estructura fina reveló que un diagrama orbital de nivel de energía no describe completamente los niveles de energía de los átomos. Esta fina estructura también proporcionó evidencia clave en ese momento de la existencia de espín electrónico, que se utilizó no solo para dar una explicación cualitativa para los multipletes sino también para proporcionar cálculos altamente precisos de las divisiones multiplete.
Acoplamiento Spin-Orbit
Especificar la configuración orbital de un átomo no identifica de manera única el estado electrónico del átomo porque el momento angular orbital, el momento angular de giro y el momento angular total no se especifican con precisión. Por ejemplo, en la configuración de hidrógeno 2p 1, el electrón puede estar en cualquiera de los tres orbitales p,\(m_l\) = +1, 0 y —1, y tener espines con\(m_s\) = +1/2 o —1/2. Así, hay 3 veces 2 posibilidades o estados diferentes. Además, el momento orbital y angular de espín de los electrones se combinan de múltiples maneras para producir vectores de momento angulares que son característicos de todo el átomo, no solo electrones individuales, y estas diferentes combinaciones pueden tener diferentes energías. Este acoplamiento de momento orbital y angular de espín se produce porque tanto el espín electrónico como el movimiento orbital producen momentos dipolares magnéticos. Como hemos visto anteriormente, la relación entre el momento angular y el momento magnético viene dada por la relación giromagnética. Estos dipolos magnéticos interactúan igual que dos diminutos imanes de barra que se atraen y repelen entre sí. Esta interacción se llama interacción espín-órbita. La energía de interacción es proporcional al producto escalar de los momentos dipolares magnéticos, los cuales son proporcionales a los vectores de momento angulares.
\[E_{s-o} = \lambda S \cdot L \label{8.8.1}\]
\[\hat {H} _{s-o} = \lambda \hat {S} \cdot \hat {L} \label {8.8.2}\]
donde\(\lambda\) representa la constante de proporcionalidad y se denomina constante de acoplamiento espín-órbita. La interacción espín-órbita acopla el movimiento de espín y el movimiento orbital de todos los electrones juntos. Este acoplamiento significa que las funciones de onda exactas no son funciones propias de los operadores de giro y momento angular orbital por separado. Más bien, se requiere que el momento angular total J = L+S, la suma vectorial del giro y el momento angular orbital, se acople para una descripción completamente precisa del sistema. Tratar de describir el sistema acoplado en términos de giro y momento angular orbital por separado es análogo a tratar de describir las posiciones de dos barras magnéticas acopladas independientemente. No se puede hacer; se debe tomar en cuenta su interacción.
Necesitamos ser capaces de identificar los estados electrónicos que resultan de una configuración electrónica dada y determinar sus energías relativas. Un estado electrónico de un átomo se caracteriza por una energía específica, función de onda (incluyendo espín), configuración electrónica, momento angular total y la forma en que los momentos orbitales y angulares de espín de los diferentes electrones se acoplan entre sí. Hay dos descripciones para el acoplamiento del momento angular. Uno se llama acoplamiento j-j, y el otro se llama acoplamiento L-S. El esquema de acoplamiento j-j se utiliza para elementos pesados (Z > 40), y el esquema de acoplamiento L-S se utiliza para los elementos más ligeros. El acoplamiento L-S también se llama acoplamiento R-S o Russell-Saunders.
Acoplamiento L-S
En el acoplamiento L-S, los momentos orbitales y angulares de espín de todos los electrones se combinan por separado
\[L = \sum _i l_i \label{8.8.3}\]
\[S = \sum _i S_i \label {8.8.4}\]
El vector de momento angular total es entonces la suma del vector de momento angular orbital total y el vector de momento angular de giro total.
\[J = L + S \label {8.8.5}\]
El resultado de estas sumas vectoriales se especifica en un código que se denomina símbolo de término Russell-Saunders, y cada símbolo de término identifica un nivel de energía del átomo. En consecuencia, los niveles de energía también se denominan términos. Un símbolo de término tiene la forma
\[\Large ^{2s+1} L_J\]
donde la letra de código que se utiliza para el número cuántico de momento angular orbital total L = 0, 1, 2, 3, 4, 5 es S, P, D, F, G, H, respectivamente. Observe cómo este código coincide con el utilizado para los orbitales atómicos. El superíndice\(2S+1\) da la multiplicidad de espín del estado, donde S es el número cuántico de momento angular de giro total. La multiplicidad de espín es el número de estados de giro asociados a un estado electrónico dado. Para no confundir la letra de código S para el momento angular orbital con el número cuántico de giro S, se debe examinar el contexto en el que se usa cuidadosamente. En el término símbolo, el subíndice\(J\) da el número cuántico de momento angular total. Debido al acoplamiento espín-órbita, solo\(J\) y\(M_J\) son números cuánticos válidos, pero debido a que el acoplamiento espín-órbita es débil\(L\)\(M_L\),\(S\),, y\(M_S\) todavía sirven para identificar y caracterizar los estados para los elementos más ligeros.
Por ejemplo, el estado fundamental, es decir, el estado de energía más baja, del átomo de hidrógeno corresponde a la configuración electrónica en la que el electrón ocupa el orbital espacial 1s y puede tener espín\(\alpha\) o espín\(\beta\). El término símbolo para el estado fundamental es\(^2 S_{1/2}\), que se lee como “doblete S 1/2”. El número cuántico de espín es 1/2 por lo que el superíndice\(2S+1 = 2\), lo que da la multiplicidad de espín del estado, es decir, el número de estados de giro es igual a 2 correspondientes a\(\alpha\) y\(\beta\). El símbolo\(S\) en el término indica que el número cuántico de momento angular orbital total es 0 (Para el estado fundamental del hidrógeno, solo hay un electrón y está en un s-orbital con\(l = 0\)). El subíndice ½ se refiere al número cuántico de momento angular total. El momento angular total es la suma del espín y los momentos angulares orbitales para los electrones en un átomo. En este caso, el número cuántico de momento angular total es solo el número cuántico de momento angular de giro, ½, ya que el momento angular orbital es cero. El estado fundamental tiene una degeneración de dos debido a que el momento angular total puede tener una proyección del eje z de\(+\frac {1}{2} \hbar\) o\(-\frac {1}{2} \hbar\), correspondiente a\(m_J\) = +1/2 o -1/2 resultante de los dos estados de espín electrónico\(\alpha\) y\(\beta\). También podemos decir, de manera equivalente, que el término estado fundamental o nivel de energía es doblemente degenerado.
Ejercicio\(\PageIndex{1}\)
Escriba el término símbolo para un estado que tenga 0 tanto para los números cuánticos de giro como de momento angular orbital.
Ejercicio\(\PageIndex{2}\)
Escriba el símbolo del término para un estado que tenga 0 para el giro y 1 para los números cuánticos de momento angular orbital
Reglas de selección de Russell-Saunders
También existen configuraciones orbitales excitadas o de mayor energía. El átomo de hidrógeno puede absorber energía, y el electrón puede ser promovido a un orbital de mayor energía. Los estados electrónicos que resultan de estas configuraciones orbitales excitadas también se caracterizan o etiquetan por símbolos de término. Los detalles de cómo determinar el término símbolos para los átomos de múltiples electrones y para los casos en los que tanto el momento orbital como el angular de espín difieren de cero se dan en otra parte, junto con reglas para determinar las energías relativas de los términos.
Hemos encontrado que las reglas de selección para un solo electrón que se mueve de un orbital atómico a otro son
\[ \Delta l = \pm 1 \label{8.8.6}\]
\[ \Delta m_l = 0, \pm 1 \label {8.8.7}\]
Para un átomo como un todo en el límite del acoplamiento L-S, las reglas de selección Russell-Saunders son
\[ \Delta S = 0 \label{8.8.8}\]
\[\Delta L = 0, \pm 1 \label{8.8.9}\]
\[\Delta J = 0, \pm 1 \label {8.8.10}\]
Sin embargo,\(J =0\) la\(J= 0\) transición está prohibida
\[\Delta m_J = 0, \pm 1 \label {8.8.11}\]
Sin embargo, el\(m_J = 0\) to\(m_J = 0\) está prohibido si\(\Delta J = 0\)
Estas reglas de selección son el resultado de las propiedades generales del momento angular, como la conservación del momento angular y las relaciones de conmutación.
Ahora queremos aplicar estas ideas para entender por qué la estructura multiplete se encuentra en el espectro de luminiscencia del hidrógeno y los iones de electrones simples. Como hemos dicho, la\(H_{\alpha}\) línea de la serie Balmer a 656.279 nm puede entenderse como debida a una transición de un electrón en un orbital atómico n = 3 a un orbital atómico n = 2. Cuando esta línea espectral fue examinada con instrumentos de alta resolución, se encontró que en realidad era un doblete, es decir, dos líneas separadas por 0.326 cm-1.
Hay 9 orbitales degenerados asociados con el nivel n = 3, y 4 asociados con el nivel n = 2. Dado que un electrón puede estar en cualquier orbital con cualquiera de dos espines, esperamos que el número total de estados sea el doble del número de orbitales. El número de orbitales viene dado por n2 por lo que debe haber 8 estados asociados con n = 2 y 18 estados asociados con n = 3. Utilizando las ideas de adición vectorial de momento angular, se dan en Tabla los términos que resultan de tener un electrón en cualquiera de estos orbitales\(\PageIndex{1}\).
|
|
|
|
|---|---|---|
| 1s 1 | 2 S 1 /2 | 2 |
| 2s 1 | 2 S 1 /2 | 2 |
| 2p 1 | 2 P 1 /2, 2 P 3 /2 | 2, 4 |
| 3s 1 | 2 S 1 /2 | 2 |
| 3p 1 | 2 P 1 /2, 2P 3 /2 | 2, 4 |
| 3d 1 | 2 D 3 /2, 2D 5 /2 | 4, 6 |
\(\PageIndex{1}\)La tabla muestra que hay 3 términos asociados con n = 2, y 5 términos asociados con n = 3. En principio, cada término puede tener una energía diferente. La degeneración de cada término está determinada por el número de proyecciones que el vector de momento angular total tiene sobre el eje z. Estas proyecciones dependen del número cuántico mJ, que va de +J a — J en pasos enteros. J es el número cuántico de momento angular total, que viene dado por el subíndice en el símbolo del término. Esta relación entre mJ y J (mJ varía de +J a — J en pasos enteros) es cierta para cualquier vector de momento angular.
Ejercicio\(\PageIndex{3}\)
Confirmar que los símbolos de término en la Tabla 8. son correctos.
Ejercicio\(\PageIndex{4}\)
Confirmar que los valores para la degeneración en Tabla\(\PageIndex{1}\) son correctos y que el número total de estados suman 8 para n = 2 y 18 para n = 3.
Las energías de los términos dependen del acoplamiento espín-órbita y correcciones relativistas que necesitan ser incluidas en el operador hamiltoniano para proporcionar una descripción más completa del átomo de hidrógeno. Como consecuencia de estos efectos, todos los términos con los mismos números cuánticos n y J tienen la misma energía mientras que los términos con valores diferentes para n o J tienen energías diferentes. El término teórico splittings dado por H.E. White, Introducción a los espectros atómicos (McGraw-Hill, Nueva York, 1934) pp. 132-137. se muestran en la Figura\(\PageIndex{8}\) .2.

La figura\(\PageIndex{2}\) muestra 5 transiciones permitidas para el electrón en los estados asociados con n = 3 a los estados asociados con n = 2. De estos cinco, dos son los más intensos y se encargan de la estructura del doblete. Estas dos transiciones están indicadas por las líneas negras anchas en la parte inferior de la figura para corresponder a las líneas observadas en el espectro fotográfico mostrado en la figura\(\PageIndex{8}\) .2. Las otras transiciones contribuyen al ancho de estas líneas o no se observan. El valor teórico para la división doblete es de 0.328 cm-1, lo que está en excelente acuerdo con el valor medido de 0.326 cm-1. El valor de 0.328 cm-1 se obtiene tomando la diferencia, 0.364 — 0.036 cm-1, en el término splittings.
Como acabamos de ver, los estados electrónicos, identificados por el término símbolos, son esenciales para comprender los espectros y la estructura del nivel de energía de los átomos, pero también es importante asociar el término símbolos y estados con las configuraciones de electrones orbitales. Las configuraciones orbitales nos ayudan a comprender muchas de las características generales o gruesas de los espectros y son necesarias para producir una imagen física de cómo cambia la densidad de electrones debido a una transición espectroscópica.
Ejercicio\(\PageIndex{5}\)
Utilice las reglas de selección Russell-Saunders para determinar qué transiciones contribuyen a la\(H_{\alpha}\) línea en el espectro de hidrógeno.
Efectos de Campo Magnético
El efecto Zeeman que se describió en la Sección 8.4 solo consideró el movimiento orbital del electrón y no incluyó el momento angular de giro y el momento magnético de espín. Para un análisis más completo del efecto Zeeman asociado a la transición n = 2 a n = 1 en el átomo de hidrógeno, necesitamos usar el término símbolos para los estados, examinar cómo se elimina la degeneración m J por el campo magnético y determinar qué transiciones entre los estados están permitidas.
Los estados involucrados en una transición de un electrón desde el orbital atómico 2p al orbital atómico 1s (donde el átomo de hidrógeno va de la configuración 2p 1 a la configuración 1s 1) se identifican en la Tabla\(\PageIndex{8}\) .1. La configuración 2p 1 produce términos 2P 3/2 y 2P 1/2 siendo este último menor en energía en 0.364 cm -1 como se muestra en la Figura\(\PageIndex{8}\) .2. La configuración 1s 1 corresponde a un término 2S 1/2, que también se muestra en la Figura\(\PageIndex{2}\).
La energía orbital en un campo magnético fue dada por la Ecuación\ ref {8.8.12}, la cual se repite aquí.
\[ \left \langle E \right \rangle = E_0 + \mu _B B_z m_l \label {8.8.12}\]
Esta ecuación puede generalizarse cambiando el número cuántico de momento angular a J y agregando un factor g para tener en cuenta las diferentes relaciones giromagnéticas
\[ \left \langle E \right \rangle = E_0 + gm_J \mu _B B_z \label {8.8.13}\]
Mientras que el factor g es igual a 2 para un electrón libre o un electrón en un orbital s, el factor g de un electrón se ve afectado por el acoplamiento espín-órbita. Para el caso del acoplamiento L-S, el factor g viene dado por
\[ g = 1 + \frac {J(J + 1) + S( S + 1) - L (L + 1)}{2J (J + 1)} \label {8.8.14}\]
Para identificar cómo cambia la energía de los estados en un campo eléctrico solo necesitamos considerar el factor GmJ en la Ecuación ya que B, que es el magnetón de Bohr, es una constante y la energía cambia solo escala con\(B_z\), que es el campo magnético. En consecuencia, podemos describir las divisiones en términos de unidades gm J donde una unidad GMj es el producto\(\mu _B B_z\).
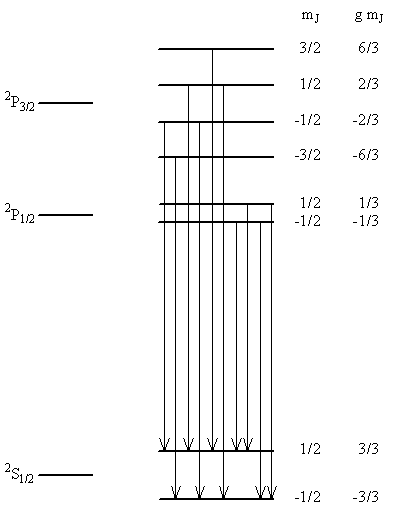
En la\(\PageIndex{3}\) tabla se enumeran las cantidades necesarias para el análisis del efecto Zeeman. La información de esta tabla muestra que el\(2P_{3/2}\) término se divide en 4 componentes. Dos componentes se mueven hacia arriba en energía 6/3 unidades y 2/3 unidades, respectivamente, y dos se mueven hacia abajo —6/3 y —2/3 unidades. El término 2P 1/2 se divide en dos componentes. Uno se mueve hacia arriba 1/3 unidad, y el otro se mueve hacia abajo 1/3 unidad. El 2S 1 /2 también se divide en dos componentes, cada uno moviendo 1 unidad hacia arriba y hacia abajo, respectivamente. Las energías de estos estados en un campo magnético junto con las transiciones permitidas entre ellos se ilustran en la Figura\(\PageIndex{3}\). La adición de momentum angular de giro ha complicado mucho más la situación. Anteriormente consideramos un efecto Zeeman que producía 3 líneas espectrales a partir de una, ahora 2 líneas se convierten en 10 líneas en un campo magnético. Estas 10 líneas corresponden a 10 posibles transiciones diferentes del electrón desde la configuración 2p 1 a la configuración 1s 1. Estas transiciones producen dos multipletes en el espectro, uno de 6 líneas y uno de 4 líneas.
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|
|
\(2^P_{3/2}\)
|
3/2
|
1
|
1/2
|
4/3
|
3/2
|
6/3
|
|
1/2
|
2/3
|
|||||
|
-1/2
|
-2/3
|
|||||
|
-3/2
|
-6/3
|
|||||
|
\(^2P_{1/2}\)
|
1/2
|
1
|
1/2
|
2/3
|
1/2
|
1/3
|
|
-1/2
|
-1/3
|
|||||
|
\(^2S_{1/2}\)
|
1/2
|
0
|
½
|
2
|
1/2
|
1
|
|
-1/2
|
-1
|
Ejercicio\(\PageIndex{6}\)
Usando la información de la Figura\(\PageIndex{8}\) .3, (a) determinar el espaciado entre las líneas en los dos multipletes en unidades de\(\mu _B B_z\), (b) determinar la magnitud de\(\mu _B B_z\)</sub> para un campo de 10,000 Gauss y para un campo de 1 Tesla, (c) aproximadamente cuál es la separación de los dos multipletes en números de onda, (d) dibujar un boceto que muestre los espectros de campo encendido y campo apagado que podría registrar en el laboratorio para la\(2p \rightarrow 1s\) transición, y (e) a partir de las transiciones permitidas que se muestran en la figura y considerando las que no ocurren, determinar cuáles deben ser las reglas de selección para ΔS, ΔL, ΔJ, y ΔMJ.


