9.4: El Método Variacional
- Page ID
- 71180
En esta sección introducimos el potente y versátil método variacional y lo utilizamos para mejorar las soluciones aproximadas que encontramos para el átomo de helio utilizando la aproximación electrónica independiente. Una forma de tomar en cuenta la repulsión electrón-electrón es modificar la forma de la función de onda. Una modificación lógica es cambiar la carga nuclear, Z, en las funciones de onda a una carga nuclear efectiva, de +2 a un valor menor,\(\zeta\) (llamado zeta) o\(Z_{eff}\). El fundamento para hacer esta modificación es que un electrón protege parcialmente la carga nuclear del otro electrón, como se muestra en la Figura\(\PageIndex{1}\).

Una región de densidad de carga negativa entre uno de los electrones y el núcleo +2 hace que la energía potencial entre ellos sea más positiva (disminuye la atracción entre ellos). Podemos efectuar este cambio matemáticamente usando\(\zeta < 2\) en la expresión wavefunction. Si el blindaje estuviera completo, entonces\(\zeta\) equivaldría a 1. Si no hay blindaje, entonces\(\zeta = 2\). Entonces, una manera de tomar en cuenta la interacción electrón-electrón es diciendo que produce un efecto de blindaje. El blindaje no es cero, y no está completo, por lo que la carga nuclear efectiva está entre uno y dos.
En general, una teoría debe ser capaz de hacer predicciones con antelación al conocimiento del resultado experimental. En consecuencia, se necesita un principio y método para elegir el mejor valor para\(\zeta\) o cualquier otro parámetro ajustable que se va a optimizar en un cálculo. El Principio Variacional proporciona el criterio y método requeridos. El Principio Variacional dice que el mejor valor para cualquier parámetro variable en una función de onda aproximada es el valor que da la energía más baja para el estado fundamental; es decir, el valor que minimiza la energía. El método variacional es el procedimiento que se utiliza para encontrar la energía más baja y los mejores valores para los parámetros variables.
El principio variacional significa que el valor de expectativa para la energía de unión obtenida usando una función de onda aproximada y el operador hamiltoniano exacto será mayor o igual que la energía verdadera para el sistema. Esta idea es realmente poderosa. Cuando se implementa, nos permite encontrar la mejor función de onda aproximada a partir de una función de onda dada que contiene uno o más parámetros ajustables, llamada función de onda de prueba. Una declaración matemática del principio variacional es
\[ \left \langle E_{trial} \right \rangle \ge E_{true} \label {9-31}\]
donde
\[ \left \langle E_{trial} \right \rangle = \dfrac {\int \psi _{trial} ^* \hat {H} \psi _{trial} d \tau}{\int \psi _{trial} ^* \psi _{trial} d\tau } \label {9-32}\]
A menudo, el valor de expectativa y las integrales de normalización en Ecuación se\(\ref{9-32}\) pueden evaluar analíticamente. Para el caso de Él descrito anteriormente, la función de onda de prueba es la función de onda del producto dada por la Ecuación\ ref {9-13}:
\[\psi (r_1 , r_2) \approx \varphi (r_1) \varphi (r_2) \label {9-13}\]
el parámetro ajustable o variable en la función de onda de prueba es la carga nuclear efectiva\(\zeta\), y el hamiltoniano es la forma completa que se da a continuación.
\[\hat {H} = -\dfrac {\hbar ^2}{2m} \nabla^2_1 - \dfrac {\zeta e^2}{4 \pi \epsilon _0 r_1} - \dfrac {\hbar ^2}{2m} \nabla ^2_2 - \dfrac {\zeta e^2}{4 \pi \epsilon _0 r_2} + \dfrac {e^2}{4 \pi \epsilon _0 r_12} \label {9-9}\]
Cuando se calcula el valor de expectativa para la energía de prueba para helio, el resultado es una función que depende del parámetro ajustable,\(\zeta\).
\[ E_{trial} (\zeta) = \dfrac {\mu e^4}{4 \epsilon ^2_0 h} \left ( \zeta ^2 - \dfrac {27}{8} \zeta \right ) \label {9-33}\]
Esta función se muestra en la Figura\(\PageIndex{2}\). De acuerdo con el principio de variación, el valor mínimo de la energía en esta gráfica es la mejor aproximación de la energía verdadera del sistema, y el valor asociado de\(\zeta\) es el mejor valor para el parámetro ajustable.
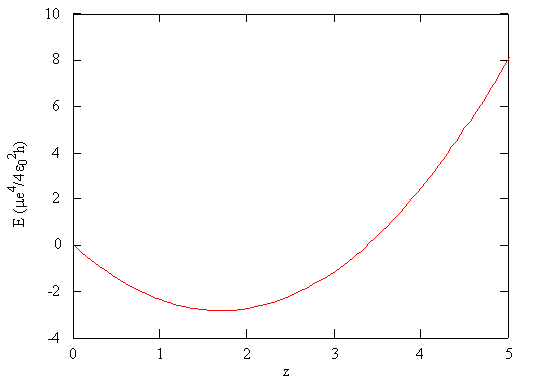
De acuerdo con el principio de variación, el valor mínimo de la energía variacional (Ecuación\(\ref{9-32}\)) de una función de onda de prueba es la mejor aproximación de la energía verdadera del sistema.
Usando la función matemática para la energía de un sistema, la energía mínima con respecto al parámetro ajustable se puede encontrar tomando la derivada de la energía con respecto a ese parámetro, estableciendo la expresión resultante igual a cero, y resolviendo para el parámetro, en este caso\(\zeta\). Este es un método estándar en cálculo para encontrar máximos y mínimos.
Ejercicio\(\PageIndex{2}\)
Encuentre el valor para\(\zeta\) que minimice la energía de unión de helio y compare la energía de unión con el valor experimental. ¿Cuál es el porcentaje de error en el valor calculado?
Cuando se realiza este procedimiento para He, encontramos\(\zeta = 1.6875\) y la energía aproximada que calculamos utilizando este tercer método de aproximación,\(E \approx = -77.483\; eV\). La tabla\(\PageIndex{1}\) muestra que se obtiene una mejora sustancial en la precisión de la energía de unión calculada mediante el uso de blindaje para dar cuenta de la interacción electrón-electrón. Incluir el efecto del blindaje electrónico en la función de onda reduce el error en la energía de unión a aproximadamente 2%. Esta idea es muy simple, elegante y significativa.
|
|
|
|---|---|
|
|
|
| Perturbación de primer orden |
|
|
|
|
|
|
|
La mejora que hemos visto en los cálculos de energía total utilizando un parámetro variable\(\zeta\) indica que una contribución importante de la interacción electrón-electrón o repulsión a la energía de unión total surge del hecho de que cada electrón protege la carga nuclear del otro electrón. Es razonable suponer que los electrones son independientes; es decir, que se mueven independientemente, pero se debe tomar en cuenta el blindaje para afinar las funciones de onda. La inclusión de parámetros optimizables en la función de onda nos permite desarrollar una imagen física clara de las consecuencias de nuestro cálculo de variación. El cálculo correcto de las energías es importante, y también es importante poder visualizar las densidades de electrones para sistemas multielectrónicos. En las dos secciones siguientes, tomamos un descanso temporal de nuestra consideración de los métodos de aproximación para examinar más de cerca las funciones de onda multielectrónica.


