9.5: Funciones de Onda de un solo electrón y funciones básicas
- Page ID
- 71127
Encontrar las funciones de onda de un solo electrón más útiles para servir como bloques de construcción para una función de onda multielectrónica es uno de los principales desafíos para encontrar soluciones aproximadas a la ecuación de Schrödinger multielectrón. Las funciones deben ser diferentes para diferentes átomos porque la carga nuclear y el número de electrones son diferentes. La atracción de un electrón para el núcleo depende de la carga nuclear, y la interacción electrón-electrón depende del número de electrones.
Como vimos en nuestros métodos iniciales de aproximación, el lugar más sencillo para comenzar a encontrar funciones de onda de un solo electrón razonables para átomos de múltiples electrones es con los orbitales atómicos producidos en el tratamiento cuántico del hidrógeno, los llamados orbitales espín “hidrogénicos”. Estos orbitales atómicos tradicionales, con algunas modificaciones, dan resultados calculados bastante razonables y todavía se utilizan ampliamente para comprender conceptualmente los átomos de múltiples electrones. En esta sección y en el Capítulo 10 exploraremos algunas de las muchas otras funciones de un solo electrón que también pueden ser utilizadas como orbitales atómicos.
Los orbitales espín hidrogénicos utilizados como componentes de sistemas multielectrónicos se identifican de la misma manera que lo son para el átomo de hidrógeno. Cada spin-orbital consiste en una función de onda espacial, especificada por los números cuánticos (n,\(l , m_l\)) y denotada ls, 2s, 2p, 3s, 3p, 3d, etc, multiplicada por una función de giro, especificada por el número cuántico\(m_s\) y denotada\(\alpha\) o\(\beta\). En nuestros métodos de aproximación inicial, ignoramos los componentes de espín de los orbitales hidrogénicos, pero deben ser considerados para desarrollar una descripción completa de los sistemas multielectrónicos. El subíndice sobre el argumento de la función espacial revela qué electrón se está describiendo (\(r_1\)es un vector que hace referencia a las coordenadas del electrón 1, por ejemplo). No se da ningún argumento para la función spin. Un ejemplo de un spin-orbital para el electrón 2 en un\(3p_z\) orbital:
\[ | \varphi _{3p_z} \alpha (r_2) \rangle = \varphi _{3,1,0}(r_2) \alpha \label {9.5.1}\]
En la notación abreviada alternativa para este spin-orbital que se muestra a continuación, las coordenadas para el electrón 2 en la función espacial se abrevian simplemente por el número “2”, y la función espacial se representa por “\(3p_z\)” en lugar de "\(\varphi _{3,1,0}\)”. El argumento “2” dado para la función spin se refiere a la variable spin desconocida para el electrón 2. Muchas ligeras variaciones sobre estas formas taquigráficas están en uso en este y otros textos, por lo que la flexibilidad y la lectura cuidadosa son importantes.
\[ | \varphi _{3p_z}\alpha (2) \rangle = 3p_z (2) \alpha (2) \label {9.5.2}\]
En este capítulo continuaremos la tendencia de alejarnos de la escritura de funciones matemáticas específicas y hacia una representación más simbólica y condensada. Su comprensión del material en este y futuros capítulos requiere que tenga en cuenta la forma y las propiedades de las funciones específicas denotadas por los símbolos utilizados en cada ecuación.
Ejercicio\(\PageIndex{1}\)
Escribe la forma matemática completa de\(\varphi _{3pz\alpha}\) usar tantos detalles funcionales explícitos como sea posible.
Las funciones matemáticas básicas y, por lo tanto, las formas generales y los momentos angulares para los orbitales hidrogénicos son los mismos que los de los orbitales de hidrógeno. Las diferencias entre los orbitales atómicos para el átomo de hidrógeno y los utilizados como componentes en las funciones de onda para sistemas multielectrónicos se encuentran en las partes radiales de las funciones de onda y en las energías. Específicamente, las diferencias surgen de la sustitución de la carga nuclear Z en las partes radiales de las funciones de onda por un parámetro ajustable\(\zeta\) que permite variar en los cálculos de aproximación para modelar las interacciones entre los electrones. Se discutió previamente dicho procedimiento para el helio El Método Variacional. El resultado es que los electrones en orbitales con diferentes valores para el número cuántico de momento angular,\(l\), tienen diferentes energías. La figura\(\PageIndex{1}\) muestra los resultados de un cálculo mecánico cuántico sobre argón en el que se encuentra que se elimina la degeneración de los orbitales 2s y 2p, así como la degeneración de los orbitales 3s, 3p y 3d.
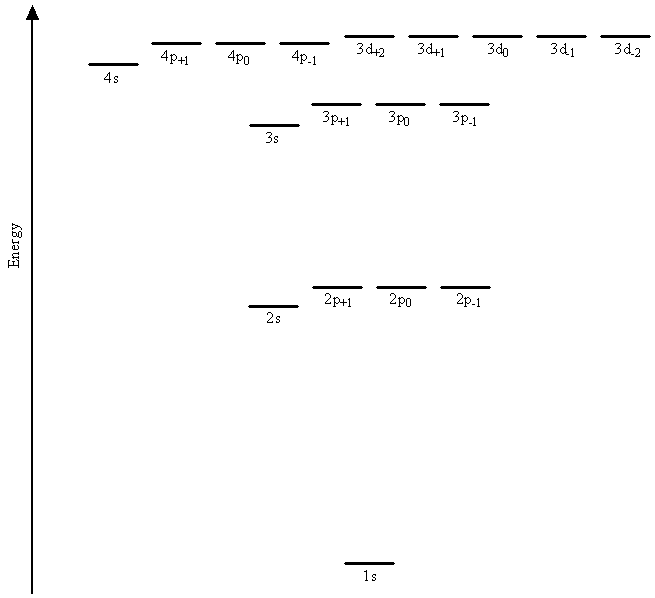
La energía de cada electrón ahora depende no sólo de su número cuántico principal,\(n\), sino también de su número cuántico de momento angular,\(l\).
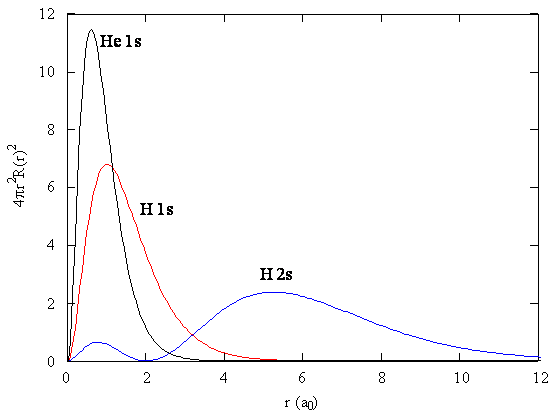
La presencia de\(\zeta\) en las porciones radiales de las funciones de onda también significa que las distribuciones de probabilidad de electrones asociadas con orbitales atómicos hidrogénicos en sistemas multielectrónicos son diferentes de las orbitales atómicas exactas para hidrógeno. La figura\(\PageIndex{2}\) compara las funciones de distribución radial para un electrón en un orbital 1s de hidrógeno (el estado fundamental), un orbital 2s en hidrógeno (una configuración excitada de hidrógeno) y un orbital 1s en helio que se describe por el mejor valor variacional de\(\zeta\). Nuestro uso de orbitales similares a hidrógeno en cálculos mecánicos cuánticos para átomos multielectrónicos nos ayuda a interpretar nuestros resultados para átomos multielectrónicos en términos de las propiedades de un sistema que podemos resolver exactamente.
Ejercicio\(\PageIndex{2}\)
Analice Figura\(\PageIndex{2}\) y escriba un párrafo sobre lo que puede discernir sobre los tamaños relativos del hidrógeno del estado fundamental, el hidrógeno del estado excitado y los átomos de helio del estado fundamental.
Si bien proporcionan puntos de paso útiles para comprender los resultados computacionales, nada requiere que usemos las funciones hidrogénicas como bloques de construcción para las funciones de onda de múltiples electrones. En la práctica, la parte radial de la órbita atómica hidrogénica presenta una dificultad computacional debido a que la función radial tiene nodos, lóbulos positivos y negativos, y variaciones pronunciadas que hacen lenta la evaluación precisa de integrales por computadora. En consecuencia, se utilizan generalmente otros tipos de funciones en la construcción de funciones multi-electrón. Estos suelen estar relacionados con los orbitales hidrogénicos para ayudar en el análisis de la estructura electrónica molecular. Por ejemplo, los orbitales atómicos tipo Slater (STO), designados a continuación como\(S_{nlm} (r, \theta , \varphi )\), evitan las dificultades impuestas por las funciones hidrogénicas. Las STO, que llevan el nombre de su creador, John Slater, fueron las primeras funciones alternativas que se utilizaron ampliamente en los cálculos. Los STO no tienen ningún nodo radial, pero aún contienen un parámetro variacional\(\zeta\) (zeta), que corresponde a la carga nuclear efectiva en los orbitales hidrogénicos. En Ecuación\(\ref{9-36}\) y en otras partes de este capítulo, la distancia\(r\),, se mide en unidades del radio de Bohr,\(a_0\).
\[ S_{nlm} (r, \theta , \varphi ) = \dfrac {(2 \zeta )^{n+1/2}}{[(2n)!]^{1/2}} r^{n-1} e^{-\zeta r } Y^m_l (\theta , \varphi ) \label {9-36}\]
Ejercicio\(\PageIndex{3}\)
- Escriba las partes radiales de los orbitales atómicos 1s, 2s y 2p para hidrógeno.
- Escriba las partes radiales de los orbitales de tipo Slater—type (STO) n = 1 y n = 2.
- Verifique que las cinco funciones anteriores estén normalizadas.
- Grafica estas cinco funciones, midiendo r en unidades del radio Bohr.
- Grafique las densidades de probabilidad radial para estos orbitales. Ponga el orbital de hidrógeno y el STO correspondiente en la misma gráfica para que puedan compararse fácilmente.
- Ajustar el parámetro zeta\(\zeta\) en cada caso para dar la mejor coincidencia de la densidad de probabilidad radial para el STO con la del orbital de hidrógeno correspondiente.
- Comentar las similitudes y diferencias entre los orbitales de hidrógeno y los STO y las densidades de probabilidad radial correspondientes.
Método Variacional Lineal
Un enfoque alternativo al problema general de introducir parámetros variacionales en las funciones de onda es la construcción de una función de onda de un solo electrón como una combinación lineal de otras funciones. Para el hidrógeno, la función radial decae, o disminuye en amplitud, exponencialmente a medida que aumenta la distancia desde el núcleo. Para el helio y otros átomos de múltiples electrones, la dependencia radial de la densidad de probabilidad total no cae como un exponencial simple al aumentar la distancia desde el núcleo como lo hace para el hidrógeno. Por lo tanto, se necesitan funciones de un solo electrón más complejas para modelar los efectos de las interacciones electrón-electrón sobre la función de distribución radial total. Una forma de obtener funciones de un solo electrón más apropiadas es usar una suma de funciones exponenciales en lugar de los orbitales espín-orbitales hidrogénicos.
Un ejemplo de tal función de onda creada a partir de una suma o combinación lineal de funciones exponenciales se escribe como
\[ \varphi _{1s} (r_1) = \sum _j c_j e^{-\zeta _j r_j /a_o} \label{9-37}\]
La combinación lineal permite ponderar los diferentes exponenciales a través de los coeficientes ajustables (cj) para cada término en la suma. Cada término exponencial tiene una tasa de decaimiento diferente a través del parámetro zeta\(\zeta _j\). Las funciones exponenciales en Ecuación\(\ref{9-37}\) se denominan funciones base. Las funciones básicas son las funciones utilizadas en combinaciones lineales para producir los orbitales de un solo electrón que a su vez se combinan para crear las funciones de onda multielectrón del producto. Originalmente las funciones básicas más populares utilizadas fueron las STO, pero hoy en día las STO no se utilizan en la mayoría de los cálculos de química cuántica. Sin embargo, a menudo son las funciones a las que se ajustan las funciones básicas más eficientes desde el punto de vista computacional.
Físicamente, los\(\zeta _j\) parámetros dan cuenta de la carga nuclear efectiva (a menudo denotada con\(Z_{eff}\). El uso de varios valores zeta en la combinación lineal permite esencialmente que la carga nuclear efectiva varíe con la distancia de un electrón desde el núcleo. Esta variación tiene sentido físicamente. Cuando un electrón está cerca del núcleo, la carga nuclear efectiva debe estar cerca de la carga nuclear real. Cuando el electrón está lejos del núcleo, la carga nuclear efectiva debería ser mucho más pequeña. Consulte las reglas de Slater para un enfoque de regla general para evaluar\(Z_{eff}\) valores.
Un término en Ecuación\(\ref{9-37}\) con un pequeño\(\zeta\) decaerá lentamente con la distancia desde el núcleo. Un término con una gran\(\zeta\) decaerá rápidamente con la distancia y no contribuirá a grandes distancias. La necesidad de tal combinación lineal de exponenciales es consecuencia de la repulsión electrón-electrón y su efecto de tamizar el núcleo para cada electrón debido a la presencia de los otros electrones.
Ejercicio\(\PageIndex{4}\)
Hacer gráficas de\(\varphi\) en Ecuación\(\ref{9-37}\) usando tres términos igualmente ponderados con\(\zeta\) = 1.0, 2.0 y 5.0. También trazar cada término por separado.
Los procedimientos computacionales en los que un parámetro exponencial como\(\zeta\) es variado se denominan más precisamente el Método Variacional No Lineal porque el parámetro variacional es parte de la función de onda y el cambio en la función y energía causado por un cambio en el parámetro no es lineal. Los valores óptimos para los parámetros zeta en cualquier cálculo particular se determinan haciendo un cálculo variacional para cada orbital para minimizar la energía del estado fundamental. Cuando este cálculo implica un cálculo variacional no lineal para los zetas, se requiere una gran cantidad de tiempo de computadora. El uso del método variacional para encontrar valores para los coeficientes\(\{c_j\}\), en la combinación lineal dada por la Ecuación\(\ref{9-37}\) anterior se denomina Método Variacional Lineal porque la función de un solo electrón cuya energía se va a minimizar (en este caso\(\varphi _{1s}\)) depende linealmente sobre los coeficientes. Si bien la idea es la misma, suele ser mucho más fácil implementar el método variacional lineal en la práctica.
Los cálculos variacionales no lineales son extremadamente costosos en términos de tiempo de computadora porque cada vez que se cambia un parámetro zeta, todas las integrales necesitan ser recalculadas. En la variación lineal, donde solo se varían los coeficientes en una combinación lineal, las funciones base y las integrales no cambian. En consecuencia, se eligió un conjunto óptimo de parámetros zeta a partir de cálculos variacionales en muchos sistemas pequeños de múltiples electrones, y estos valores, que se dan en la Tabla\(\PageIndex{1}\), generalmente se pueden usar en las STO para otros sistemas y sistemas más grandes.
| Atom | \(\zeta _{1s}\) | \(\zeta _{2s,2p}\) |
|---|---|---|
| H | 1.24 | |
| Él | 1.69 | |
| Li | 2.69 | 0.80 |
| Be | 3.68 | 1.15 |
| B | 4.68 | 1.50 |
| C | 5.67 | 1.72 |
| N | 6.67 | 1.95 |
| O | 7.66 | 2.25 |
| F | 8.56 | 2.55 |
| Ne | 9.64 | 2.88 |
Ejercicio\(\PageIndex{5}\)
Compare el valor\(\zeta _{1s}\) = 1.24 en Tabla\(\PageIndex{1}\) para hidrógeno con el valor que obtuvo en Ejercicio\(\PageIndex{3}\). y comente las posibles razones de cualquier diferencia. ¿Por qué los valores zeta son mayores para 1s que para orbitales 2s y 2p? ¿Por qué los\(\zeta _{1s}\) valores aumentan esencialmente en una unidad por cada elemento de He a Ne mientras que el aumento para los\(\zeta _{2s, 2p}\) valores es mucho menor?
La discusión anterior nos da algunas ideas nuevas sobre cómo escribir funciones de onda de un solo electrón flexibles y útiles que puedan ser utilizadas para construir funciones de onda multi-electrón para cálculos variacionales. Las funciones de un solo electrón construidas a partir del enfoque de función base son flexibles porque tienen varios parámetros ajustables y útiles porque los parámetros ajustables aún tienen interpretaciones físicas claras. Tales funciones serán necesarias en el método Hartree-Fock discutido en otra parte.


