Saltar al contenido principal
LibreTexts Español

2.2: Representación gráfica y relación con Euler

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    70086

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

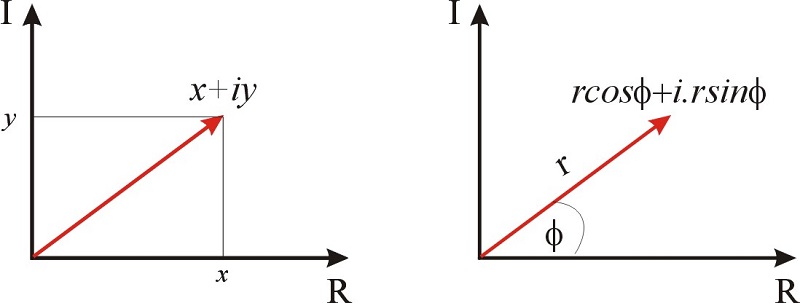
    Los números complejos se pueden representar gráficamente como un punto en un plano de coordenadas. En las coordenadas cartesianas, el\(x\) eje -se usa para la parte real del número, y el\(y\) eje -se usa para el componente imaginario. Por ejemplo, el número complejo\(x+iy\) se representa como un punto en la Figura\(\PageIndex{1}\).

    Los números complejos también se pueden representar en forma polar. Eso lo sabemos, dado un punto\((x,y)\) en el avión,\(\cos\phi=x/r\) y\(\sin\phi=y/r\). Por lo tanto, el número complejo también se\(x+iy\) puede representar como\(r\cos\phi+i r\sin\phi\).

    complex.jpg
    Figura\(\PageIndex{1}\): Representación gráfica de números complejos. (CC BY-NC-SA; Marcia Levitus)

    También podemos representar números complejos en términos de exponenciales complejos. Esto sonará raro por ahora, pero veremos lo común y útil que es esto en la química física ya que cubrimos otros temas este semestre. La relación de Euler relaciona las funciones trigonométricas con un exponencial complejo:

    \[\label{eq1} e^{\pm i\phi}=\cos\phi\pm i\sin\phi\]

    Demostraremos esta relación usando la serie Taylor más adelante.

    En resumen, el número complejo se\(\displaystyle{\color{Maroon} x+iy}\) puede expresar en coordenadas polares como\(\displaystyle{\color{Maroon}r\cos\phi+i r\sin\phi}\), y como un exponencial complejo como\(\displaystyle{\color{Maroon}r e^{i\phi}}\). Las relaciones entre\(x,y\) y\(r,\phi\) están dadas por las relaciones trigonométricas familiares:\(x=r\cos\phi\) y\(y=r\sin\phi\). Observe que

    \[r^2=x^2+y^2 \nonumber\]

    y

    \[\sin^2\phi+\cos^2\phi=1 \nonumber\]

    como sabemos del teorema de Pitágoras.

    Ejemplo\(\PageIndex{1}\)

    \(z= 1+i\)Exprese en la forma\(r e^{i\phi}\)

    Solución

    \(x = 1\)y\(y=1\).

    Sabemos que

    \(x=r\cos\phi\)y\(y=r\sin\phi\)

    Dividiendo\(y/x\), obtenemos\(y/x=\tan\phi\). En este problema\(y=x\), y por lo tanto\(\pi/4\).

    Para obtener\(r\) utilizamos\(r^2=x^2+y^2\). En este caso:

    \[x^2+y^2=2 \to r=\sqrt{2} \nonumber\]

    Por lo tanto,\(\displaystyle{\color{Maroon}z = \sqrt{2} e^{\frac{\pi}{4} i}}\)

    A partir de la ecuación\ ref {eq1} podemos ver cómo las funciones trigonométricas se pueden expresar como exponenciales complejos:

    \[ \begin{split} \cos\phi=\frac{e^{i \phi}+e^{-i \phi}}{2}\\ \sin\phi=\frac{e^{i \phi}-e^{-i \phi}}{2i} \end{split}\]

    Nuevamente, esto puede parecer extraño en este punto, pero resulta que los exponenciales son mucho más fáciles de manipular que las funciones trigonométricas (piense en multiplicar o dividir exponenciales vs. funciones trigonométricas), por lo que es común que los químicos físicos escriban ecuaciones en términos de exponenciales complejos en su lugar de cosenos y senos.

    En Ecuación\(2.1.1\) vimos eso\((x+iy)(x-iy)=x^2+y^2\). Ahora sabemos que esto es igual\(r^2\), donde\(r\) está el módulo o valor absoluto del vector representado en rojo en la Figura\(\PageIndex{1}\). Por lo tanto, el módulo de un número complejo, denotado como\(|z|\), puede calcularse como:

    \[\label{modulus} |z|^2= z z^* \to |z|=\sqrt{z z^*}\]

    Ejemplo\(\PageIndex{2}\)

    Obtener el módulo del número complejo\(z= 1+i\) (ver Ejemplo\(\PageIndex{1}\))

    Solución

    \[|z|=\sqrt{z z^*}=\sqrt{(1+i)(1-i)}=\displaystyle{\color{Maroon}\sqrt{2}} \nonumber\]

    enlaces externos

    This page titled 2.2: Representación gráfica y relación con Euler is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Marcia Levitus via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.