3.1: Serie Maclaurin
- Page ID
- 70019
Una función\(f(x)\) puede expresarse como una serie en potencias de tanto tiempo\(x\) como\(f(x)\) y todas sus derivadas son finitas en\(x=0\). Por ejemplo, vamos a probar en breve que la función se\(f(x) = \dfrac{1}{1-x}\) puede expresar como la siguiente suma infinita:
\[\label{eq1}\dfrac{1}{1-x}=1+x+x^2+x^3+x^4 + \ldots\]
Podemos escribir esta declaración de esta manera más elegante:
\[\label{eq2}\dfrac{1}{1-x}=\displaystyle\sum_{n=0}^{\infty} x^{n}\]
Si no estás familiarizado con esta notación, el lado derecho de la ecuación lee “sum from\(n=0\) to\(n=\infty\) of\(x^n.\)” When\(n=0\),\(x^n = 1\), when\(n=1\)\(x^n = x\), when\(n=2\),\(x^n = x^2\), etc (compare with Equation\ ref {eq1}). El término “serie en potencias de\(x\)” significa una suma en la que cada suma es una potencia de la variable\(x\). Tenga en cuenta que el número 1 es una potencia de\(x\) as well (\(x^0=1\)). Además, tenga en cuenta que ambas Ecuaciones\ ref {eq1} y\ ref {eq2} son exactas, no son aproximaciones.
Del mismo modo, veremos en breve que la función se\(e^x\) puede expresar como otra suma infinita en potencias de\(x\) (es decir, una serie Maclaurin) como:
\[\label{expfunction}e^x=1+x+\dfrac{1}{2} x^2+\dfrac{1}{6}x^3+\dfrac{1}{24}x^4 + \ldots \]
O, más elegantemente:
\[\label{expfunction2}e^x=\displaystyle\sum_{n=0}^{\infty}\dfrac{1}{n!} x^{n}\]
donde\(n!\) se lee “n factorial” y representa el producto\(1\times 2\times 3...\times n\). Si no estás familiarizado con las factoriales, asegúrate de entender por qué\(4! = 24\). Además, recuerda eso por definición\(0! = 1\), no cero.
En este punto deberías tener dos preguntas: 1) cómo construyo la serie Maclaurin de una función dada, y 2) por qué en la tierra querría hacer esto si\(\dfrac{1}{1-x}\) y\(e^x\) son funciones de aspecto fino como son. La respuesta a la primera pregunta es fácil, y aunque deberías saber esto por tus clases de cálculo la volveremos a revisar en un momento. La respuesta a la segunda pregunta es más complicado, y es lo que la mayoría de los estudiantes encuentran confuso sobre este tema. Discutiremos diferentes ejemplos que tienen como objetivo mostrar una variedad de situaciones en las que expresar funciones de esta manera es útil.
Cómo obtener la serie Maclaurin de una función
En general, una función de buen comportamiento (\(f(x)\)y todas sus derivadas son finitas en\(x=0\)) se expresará como una suma infinita de poderes de\(x\) así:
\[\label{eq3}f(x)=\displaystyle\sum_{n=0}^{\infty}a_n x^{n}=a_0+a_1 x + a_2 x^2 + \ldots + a_n x^n\]
Asegúrese de entender por qué las dos expresiones en la Ecuación\ ref {eq3} son formas idénticas de expresar una suma infinita. Los términos\(a_n\) se llaman los coeficientes, y son constantes (es decir, NO son funciones de\(x\)). Si terminas con la variable\(x\) en uno de tus coeficientes vuelve atrás y comprueba lo que hiciste mal! Por ejemplo, en el caso de\(e^x\) (Ecuación\ ref {expfunction}),\(a_0 =1, a_1=1, a_2 = 1/2, a_3=1/6, etc\). En el ejemplo de Ecuación\ ref {eq1}, todos los coeficientes son iguales a 1. Acabamos de ver que dos funciones muy diferentes se pueden expresar usando el mismo conjunto de funciones (los poderes de\(x\)). Lo que hace\(\dfrac{1}{1-x}\) diferente\(e^x\) son los coeficientes\(a_n\). Como veremos en breve, los coeficientes pueden ser negativos, positivos o cero.
¿Cómo calculamos los coeficientes? Cada coeficiente se calcula como:
\[\label{series:coefficients}a_n=\dfrac{1}{n!} \left( \dfrac{d^n f(x)}{dx^n} \right)_0\]
Es decir, el coeficiente\(n\) -ésimo equivale a uno sobre el factorial de\(n\) multiplicado por la\(n\) -ésima derivada de la función\(f(x)\) evaluada a cero. Por ejemplo, si queremos calcular\(a_2\) para la función\(f(x)=\dfrac{1}{1-x}\), necesitamos obtener la segunda derivada de\(f(x)\), evaluarla en\(x=0\), y dividir el resultado por\(2!\). Hazlo tú mismo y verifícalo\(a_2=1\). En el caso de\(a_0\) necesitamos la derivada de orden cero, que iguala a la función misma (es decir,\(a_0 = f(0)\), porque\(\dfrac{1}{0!}=1\)). Es importante destacar que aunque las derivadas suelen ser funciones de\(x\), los coeficientes son constantes porque se expresan en términos de las derivadas evaluadas en\(x=0\).
Nótese que para obtener una serie de Maclaurin evaluamos la función y sus derivadas en\(x=0\). Este procedimiento también se llama la expansión de la función alrededor (o alrededor de) cero. Podemos expandir funciones alrededor de otros números, y estas series se llaman series Taylor (ver Sección 3).
Ejemplo\(\PageIndex{1}\)
Obtener la serie Maclaurin de\(sin(x)\).
Solución
Necesitamos obtener todos los coeficientes (\(a_0, a_1...etc\)). Debido a que hay infinitamente muchos coeficientes, vamos a calcular unos pocos y encontraremos un patrón general para expresar el resto. Vamos a necesitar varias derivadas de\(sin(x)\), así que hagamos una tabla:
| \(n\) | \(\dfrac{d^n f(x)}{dx^n}\) | \(\left( \dfrac{d^n f(x)}{dx^n} \right)_0\) |
|---|---|---|
| \ (n\)” style="text-align:center; ">0 | \ (\ dfrac {d^n f (x)} {dx^n}\)” style="text-align:center; ">\(\sin (x)\) | \ (\ izquierda (\ dfrac {d^n f (x)} {dx^n}\ derecha) _0\)” style="text-align:center; ">0 |
| \ (n\)” style="text-align:center; ">1 | \ (\ dfrac {d^n f (x)} {dx^n}\)” style="text-align:center; ">\(\cos (x)\) | \ (\ izquierda (\ dfrac {d^n f (x)} {dx^n}\ derecha) _0\)” style="text-align:center; ">1 |
| \ (n\)” style="text-align:center; ">2 | \ (\ dfrac {d^n f (x)} {dx^n}\)” style="text-align:center; ">\(-\sin (x)\) | \ (\ izquierda (\ dfrac {d^n f (x)} {dx^n}\ derecha) _0\)” style="text-align:center; ">0 |
| \ (n\)” style="text-align:center; ">3 | \ (\ dfrac {d^n f (x)} {dx^n}\)” style="text-align:center; ">\(-\cos (x)\) | \ (\ izquierda (\ dfrac {d^n f (x)} {dx^n}\ derecha) _0\)” style="text-align:center; ">-1 |
| \ (n\)” style="text-align:center; ">4 | \ (\ dfrac {d^n f (x)} {dx^n}\)” style="text-align:center; ">\(\sin (x)\) | \ (\ izquierda (\ dfrac {d^n f (x)} {dx^n}\ derecha) _0\)” style="text-align:center; ">0 |
| \ (n\)” style="text-align:center; ">5 | \ (\ dfrac {d^n f (x)} {dx^n}\)” style="text-align:center; ">\(\cos (x)\) | \ (\ izquierda (\ dfrac {d^n f (x)} {dx^n}\ derecha) _0\)” style="text-align:center; ">1 |
Recuerde que cada coeficiente es igual\(\left( \dfrac{d^n f(x)}{dx^n} \right)_0\) dividido por\(n!\), por lo tanto:
| \(n\) | \(n!\) | \(a_n\) |
|---|---|---|
| \ (n\)” style="text-align:center; ">0 | \ (n! \)” style="text-align:center; ">1 | \ (a_n\)” style="text-align:center; ">0 |
| \ (n\)” style="text-align:center; ">1 | \ (n! \)” style="text-align:center; ">1 | \ (a_n\)” style="text-align:center; ">1 |
| \ (n\)” style="text-align:center; ">2 | \ (n! \)” style="text-align:center; ">2 | \ (a_n\)” style="text-align:center; ">0 |
| \ (n\)” style="text-align:center; ">3 | \ (n! \)” style="text-align:center; ">\(6\) | \ (a_n\)” style="text-align:center; ">\(-\dfrac{1}{6}\) |
| \ (n\)” style="text-align:center; ">4 | \ (n! \)” style="text-align:center; ">\(24\) | \ (a_n\)” style="text-align:center; ">0 |
| \ (n\)” style="text-align:center; ">5 | \ (n! \)” style="text-align:center; ">\(120\) | \ (a_n\)” style="text-align:center; ">\(\dfrac{1}{120}\) |
Esta es suficiente información para ver el patrón (puedes ir a valores más altos de\(n\) si aún no lo ves):
- los coeficientes para valores pares de\(n\) igual cero.
- los coeficientes para\(n = 1, 5, 9, 13,...\) igual\(1/n!\)
- los coeficientes para\(n = 3, 7, 11, 15,...\) igual\(-1/n!\).
Recordemos que la expresión general para una serie de Maclaurin es\(a_0+a_1 x + a_2 x^2...a_n x^n\), y sustituirla\(a_0...a_n\) por los coeficientes que acabamos de encontrar:
\[\displaystyle{\color{Maroon}\sin (x) = x - \dfrac{1}{3!} x^3+ \dfrac{1}{5!} x^5 -\dfrac{1}{7!} x^7...} \nonumber\]
Esta es una forma correcta de escribir la serie, pero en el siguiente ejemplo veremos cómo escribirla de manera más elegante como suma.
Ejemplo\(\PageIndex{2}\)
Expresa la serie Maclaurin de\(\sin (x)\) como suma.
Solución
En el ejemplo anterior encontramos que:
\[\label{series:sin}\sin (x) = x - \dfrac{1}{3!} x^3+ \dfrac{1}{5!} x^5 -\dfrac{1}{7!} x^7...\]
Queremos expresar esto como una suma:
\[\displaystyle\sum_{n=0}^{\infty}a_n x^{n} \nonumber\]
La clave aquí es expresar los coeficientes\(a_n\) en términos de\(n\). Acabamos de concluir que 1) los coeficientes para valores pares de\(n\) igual cero, 2) los coeficientes para\(n = 1, 5, 9, 13,...\) iguales\(1/n!\) y 3) los coeficientes para\(n = 3, 7, 11,...\) iguales\(-1/n!\). ¿Cómo juntamos toda esta información en una expresión única? Aquí hay tres respuestas posibles (e igualmente buenas):
- \(\displaystyle{\color{Maroon}\sin (x)=\displaystyle\sum_{n=0}^{\infty} \left( -1 \right) ^n \dfrac{1}{(2n+1)!} x^{2n+1}}\)
- \(\displaystyle{\color{Maroon}\sin (x)=\displaystyle\sum_{n=1}^{\infty} \left( -1 \right) ^{(n+1)} \dfrac{1}{(2n-1)!} x^{2n-1}}\)
- \(\displaystyle{\color{Maroon}\sin (x)=\displaystyle\sum_{n=0}^{\infty} cos(n \pi) \dfrac{1}{(2n+1)!} x^{2n+1}}\)
Esto puede parecer imposiblemente difícil de entender, pero permítame compartir algunos trucos contigo. Primero, notamos que el signo en Ecuación\ ref {series:sin} alterna, comenzando con un “+”. Una forma matemática de hacer esto es con un término\((-1)^n\) si tu suma comienza con\(n=0\), o\((-1)^{(n+1)}\) si tu suma comienza con\(n=1\). Tenga en cuenta que\(\cos (n \pi)\) hace el mismo truco.
| \(n\) | \((-1)^n\) | \((-1)^{n+1}\) | \(\cos (n \pi)\) |
|---|---|---|---|
| \ (n\)” style="text-align:center; ">0 | \ ((-1) ^n\)” style="text-align:center; ">1 | \ ((-1) ^ {n+1}\)” style="text-align:center; ">-1 | \ (\ cos (n\ pi)\)” style="text-align:center; ">1 |
| \ (n\)” style="text-align:center; ">1 | \ ((-1) ^n\)” style="text-align:center; ">-1 | \ ((-1) ^ {n+1}\)” style="text-align:center; ">1 | \ (\ cos (n\ pi)\)” style="text-align:center; ">-1 |
| \ (n\)” style="text-align:center; ">2 | \ ((-1) ^n\)” style="text-align:center; ">1 | \ ((-1) ^ {n+1}\)” style="text-align:center; ">-1 | \ (\ cos (n\ pi)\)” style="text-align:center; ">1 |
| \ (n\)” style="text-align:center; ">3 | \ ((-1) ^n\)” style="text-align:center; ">-1 | \ ((-1) ^ {n+1}\)” style="text-align:center; ">1 | \ (\ cos (n\ pi)\)” style="text-align:center; ">-1 |
Tenemos el signo correcto para cada término, pero necesitamos generar los números\(1, \dfrac{1}{3!}, \dfrac{1}{5!}, \dfrac{1}{7!},...\) Aviso que el número “1” se puede expresar como\(\dfrac{1}{1!}\). Para ello, te presentamos el segundo truco del día: usaremos la expresión\(2n+1\) para generar números impares (si comienzas tu suma con\(n=0\)) o\(2n-1\) (si empiezas en\(n=1\)). Por lo tanto, la expresión\(\dfrac{1}{(2n+1)!}\) da\(1, \dfrac{1}{3!}, \dfrac{1}{5!}, \dfrac{1}{7!},...\), que es lo que necesitamos en el primer y tercer ejemplo (cuando la suma empieza en cero).
Por último, necesitamos utilizar sólo los poderes impares de\(x\). La expresión\(x^{(2n+1)}\) genera los términos\(x, x^3, x^5...\) cuando comienzas en\(n=0\), y\(x^{(2n-1)}\) logra lo mismo cuando comienzas tu serie en\(n=1\).
¿Confundido acerca de escribir sumas usando el operador de suma\((\sum)\)? Este video ayudará a: http://tinyurl.com/lvwd36q
¿Necesitas ayuda? Los enlaces a continuación contienen ejemplos resueltos.
Enlaces externos:
Encontrar la serie maclaurin de una función I: http://patrickjmt.com/taylor-and-maclaurin-series-example-1/
Encontrar la serie maclaurin de una función II: http://www.youtube.com/watch?v = Dp2OVDuwhro
Encontrar la serie maclaurin de una función III: http://www.youtube.com/watch?v = wWe7pZjC4s8
Representación Gráfica
De la ecuación\(\ref{eq3}\) y los ejemplos que discutimos anteriormente, debe quedar claro en este punto que cualquier función cuyas derivadas sean finitas en se\(x=0\) puede expresar usando el mismo conjunto de funciones: los poderes de\(x\). Llamaremos a estas funciones el conjunto de bases. Un conjunto de bases es una colección de funciones linealmente independientes que pueden representar otras funciones cuando se usan en una combinación lineal.
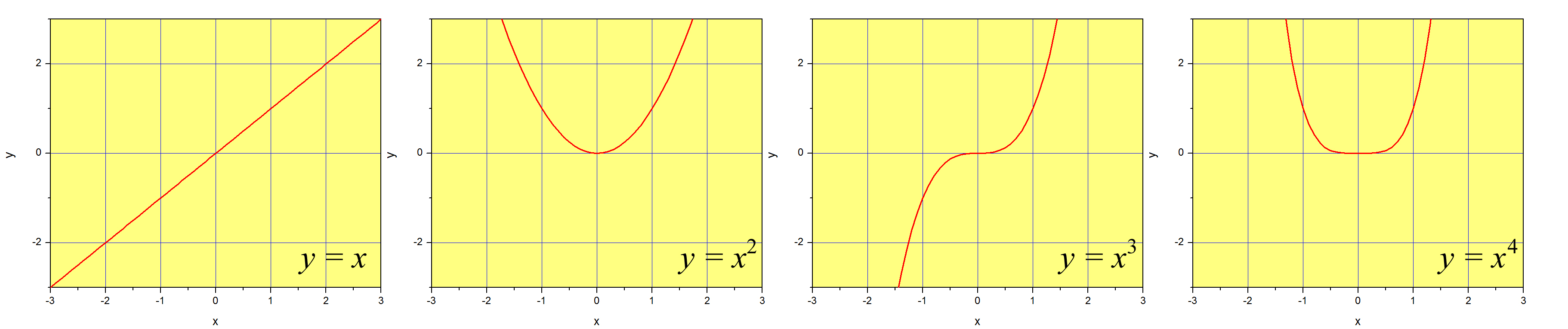
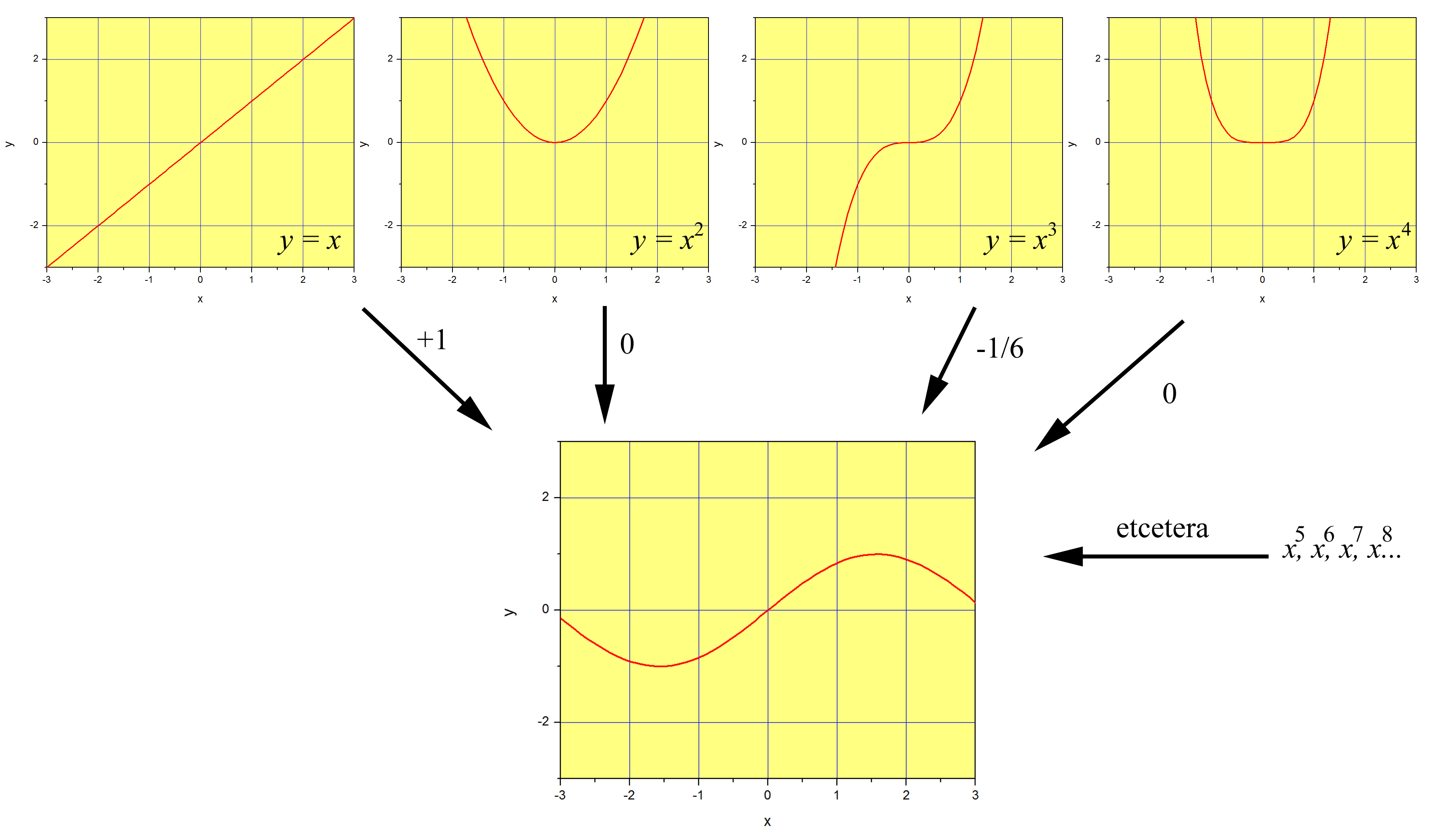
La figura\(\PageIndex{1}\) es una representación gráfica de las cuatro primeras funciones de este conjunto de bases. Para ser justos, la primera función del conjunto es\(x^0=1\), por lo que estas serían la segunda, tercera, cuarta y quinta. El conjunto completo de bases es, por supuesto, infinito en longitud. Si mezclamos todas las funciones del conjunto con pesos iguales (ponemos la misma cantidad de\(x^2\) lo que ponemos\(x^{245}\) o\(x^{0}\)), obtenemos\((1-x)^{-1}\) (Ecuación\ ref {eq1}. Si usamos solo los términos impares, alternamos el signo comenzando con un '+', y pesamos cada término cada vez menos usando la expresión\(1/(2n-1)!\) para el\(n-th\) término, obtenemos\(\sin{x}\) (Ecuación\ ref {series:sin}). Esto se ilustra en la Figura\(\PageIndex{2}\), donde multiplicamos las potencias pares de\(x\) por cero, y usamos diferentes pesos para el resto. Tenga en cuenta que lo 'etcétera' es crucial, ya que necesitaríamos incluir un número infinito de funciones para obtener la función\(\sin{x}\) exactamente.
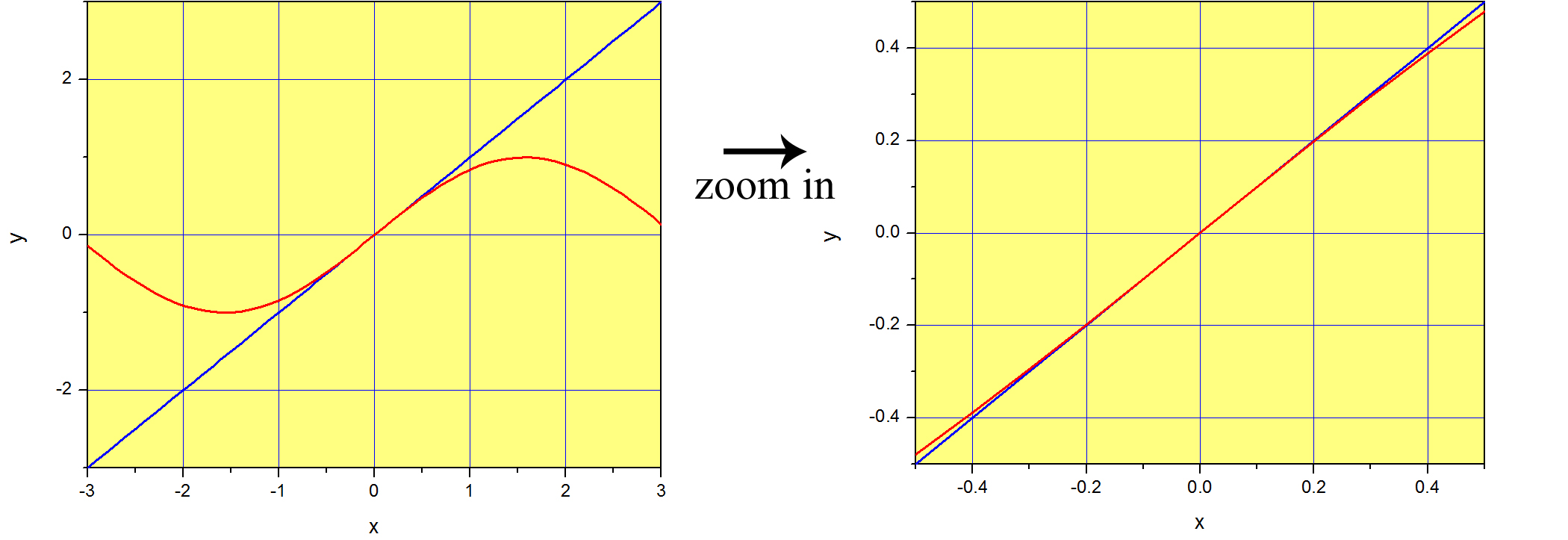
Aunque necesitamos un número infinito de términos para expresar una función exactamente (a menos que la función sea un polinomio, por supuesto), en muchos casos observaremos que el peso (el coeficiente) de cada potencia de\(x\) se hace cada vez más pequeño a medida que aumentamos la potencia. Por ejemplo, en el caso de\(\sin{x}\), la contribución de\(x^3\) es\(1/6 th\) de la contribución de\(x\) (en términos absolutos), y la contribución de\(x^5\) es\(1/120 th\). Esto te dice que los primeros términos son mucho más importantes que el resto, aunque todos son necesarios si queremos que la suma represente\(\sin{x}\) exactamente. ¿Y si estamos contentos con una aproximación 'bastante buena' de\(\sin{x}\)? Veamos qué pasa si usamos hasta\(x^3\) y bajamos los términos más altos. El resultado se grafica en azul en la Figura\(\PageIndex{3}\) junto con\(\sin{x}\) en rojo. Podemos ver que la función\(x-1/6 x^3\) es una muy buena aproximación de\(\sin{x}\) mientras nos mantengamos cerca de\(x=0\). A medida que nos alejamos del origen la aproximación empeora y empeora, y necesitaríamos incluir potencias superiores de\(x\) para mejorarla. Esto debería quedar claro a partir de la eq. [series:sin], ya que los términos se\(x^n\) hacen cada vez más pequeños con el aumento\(n\) si\(x\) es un número pequeño. Por lo tanto, si\(x\) es pequeño, podríamos escribir\(\sin (x) \approx x - \dfrac{1}{3!} x^3\), donde el símbolo\(\approx\) significa aproximadamente igual.
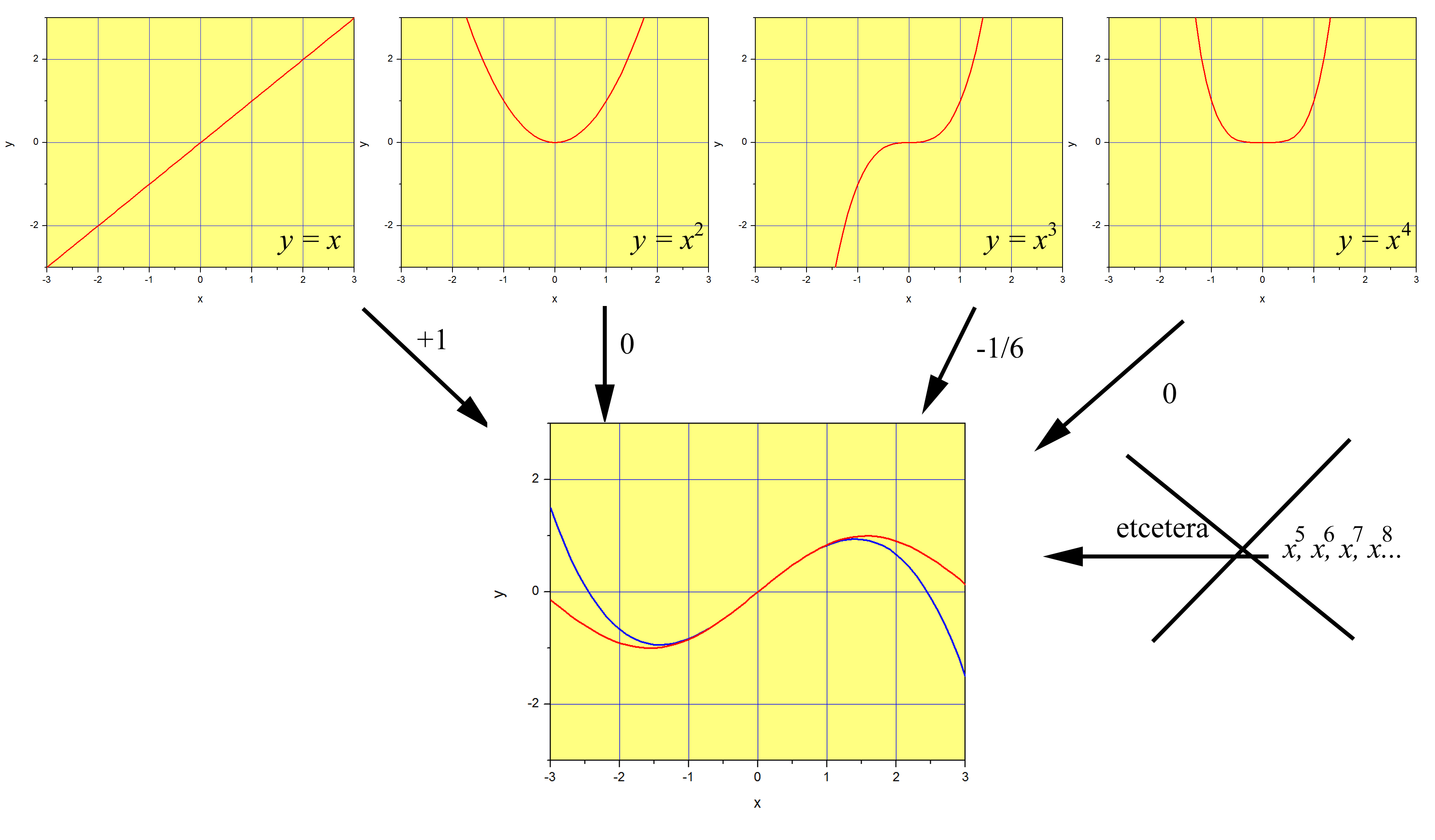
Pero, ¿por qué detenerse en\(n=3\) y no\(n=1\) o 5? El argumento anterior sugiere que la función\(x\) podría ser una buena aproximación de\(\sin{x}\) alrededor\(x=0\), cuando el término\(x^3\) es mucho menor que el término\(x\). De hecho, este es el caso, como se muestra en la Figura\(\PageIndex{4}\).
Hemos visto que podemos obtener buenas aproximaciones de una función truncando la serie (es decir, no usando los términos infinitos). Los estudiantes suelen sentirse frustrados y quieren saber cuántos términos son 'correctos'. Se necesita un poco de práctica para darse cuenta de que no hay una respuesta universal a esta pregunta. Necesitaríamos algún contexto para analizar qué tan buena aproximación estamos contentos con. Por ejemplo, ¿estamos satisfechos con el pequeño error que vemos\(x= 0.5\) en la Figura\(\PageIndex{4}\)? Todo depende del contexto. A lo mejor estamos realizando experimentos donde tenemos otras fuentes de error que son mucho peores que esto, por lo que usar un término extra no mejorará la situación general de todos modos. A lo mejor estamos realizando experimentos muy precisos donde esta diferencia es significativa. Como ve, discutir cuántos términos se necesitan en una aproximación fuera de contexto no es muy útil. Discutiremos esta aproximación particular cuando aprendamos sobre ecuaciones diferenciales de segundo orden y analicemos el problema del péndulo, así que ojalá las cosas tengan más sentido entonces.