3.2: Aproximaciones lineales
- Page ID
- 70009
Si le das un vistazo a Ecuación\(3.1.5\) verás que siempre podemos aproximar una función\(a_0+a_1x\) siempre y cuando\(x\) sea pequeña. Cuando decimos 'cualquier función', por supuesto, implicamos que la función y todas sus derivadas necesitan ser finitas en\(x=0\). Mirando las definiciones de los coeficientes, podemos escribir:
\[\label{eq1} f (x) \approx f(0) +f'(0)x\]
Llamamos a esto una aproximación lineal porque la Ecuación\ ref {eq1} es la ecuación de una línea recta. La pendiente de esta línea es\(f'(0)\) y la\(y\) -intercepción es\(f(0)\).
Una pregunta justa en este punto es '¿por qué estamos hablando siquiera de aproximaciones?' ¿Qué tiene de complicado las funciones\(\sin{x}\),\(e^x\) o\(\ln{(x+1)}\) que necesitamos buscar una aproximación? ¿Nos estamos volviendo demasiado perezosos? Para ilustrar este tema, consideremos el problema del péndulo, que resolveremos en detalle en el capítulo dedicado a las ecuaciones diferenciales. El problema se ilustra en Figura\(\PageIndex{1}\), y aquellos de ustedes que tomaron un curso de física reconocerán la siguiente ecuación, que representa la ley del movimiento de un simple péndulo. La segunda derivada se refiere a la aceleración, y el\(\sin \theta\) término se debe a la componente de la fuerza neta a lo largo de la dirección del movimiento. Esto lo discutiremos con más detalle más adelante en este semestre, así que por ahora solo acepta el hecho de que, para este sistema, la ley de Newton puede escribirse como:
\[\frac{d^2\theta(t)}{dt^2}+\frac{g}{l} \sin{\theta(t)}=0 \nonumber\]
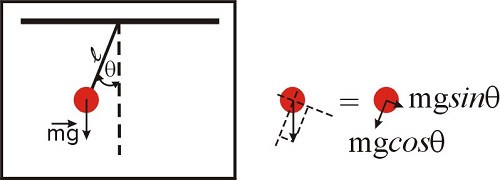
Esta ecuación debería ser fácil de resolver, ¿verdad? Tiene sólo unos pocos términos, nada demasiado elegante que no sea una función sinusoidal inocente... ¿Qué tan difícil puede ser de obtener\(\theta(t)\)? Desafortunadamente, ¡esta ecuación diferencial no tiene una solución analítica! Una solución analítica significa que la solución puede expresarse en términos de un número finito de funciones elementales (como seno, coseno, exponenciales, etc.). Las ecuaciones diferenciales a veces engañan de esta manera: se ven simples, pero pueden ser increíblemente difíciles de resolver, ¡o incluso imposibles! El hecho de que no podamos anotar una solución analítica no significa que no haya solución al problema. Puedes balancear un péndulo\(\theta(t)\) y medir y crear una tabla de números, y en principio puedes ser tan preciso como quieras ser. Sin embargo, no podrás crear una función que refleje tus resultados numéricos. Veremos que podemos resolver ecuaciones como esta numéricamente, pero no analíticamente. Decepcionante, ¿no? Bueno... no lo seas. Mucho de lo que sabemos sobre las moléculas y las reacciones químicas provino del trabajo de los químicos físicos, que saben resolver problemas mediante métodos numéricos. El hecho de que no podamos obtener una expresión analítica que describa un sistema físico o químico en particular no significa que no podamos resolver el problema numéricamente y ¡aprender mucho de todos modos!
Pero, ¿y si solo nos interesan los pequeños desplazamientos (es decir, el péndulo se balancea cerca del eje vertical en todo momento)? En este caso,\(\theta<<1\), y como vimos\(\sin{\theta}\approx\theta\) (ver Figura\(3.1.4\)). Si este es el caso, tenemos ahora:
\[\frac{d^2\theta(t)}{dt^2}+\frac{g}{l} \theta(t)=0 \nonumber\]
Como resulta, y como veremos en el Capítulo 2, en este caso es muy fácil obtener la solución que estamos buscando:
\[\theta(t)=\theta(t=0)\cos \left((\frac{g}{l})^{1/2}t \right) \nonumber\]
Esta solución es el familiar movimiento oscilatorio “de ida y vuelta” del péndulo con el que está familiarizado. Lo que quizás no sabías hasta hoy es que esta solución asume\(\sin{\theta}\approx\theta\) y por lo tanto es válida sólo si\(\theta<<1\)!
Hay muchas aproximaciones lineales 'ocultas' en las ecuaciones que has aprendido en tus cursos de física y química. Quizás recuerde que sus maestros le dijeron que una ecuación de dar es válida solo a bajas concentraciones, o bajas presiones, o bajas... ojalá consiga el punto. Un péndulo por supuesto no es particularmente interesante cuando se trata de química, pero como veremos a través de muchos ejemplos durante el semestre, las oscilaciones, en términos generales, lo son. El siguiente ejemplo ilustra el uso de series a un problema que involucra moléculas diatómicas, pero antes de discutirlo necesitamos proporcionar algunos antecedentes.
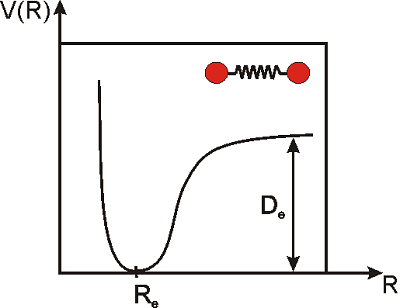
Las vibraciones de una molécula diatómica a menudo se modelan en términos del llamado potencial Morse. Esta ecuación no proporciona una descripción exacta de las vibraciones de la molécula bajo ninguna condición, pero hace un trabajo bastante bueno para muchos propósitos.
\[\label{morse}V(R)=D_e\left(1-e^{-k(R-R_e)}\right)^2\]
Aquí,\(R\) es la distancia entre los núcleos de los dos átomos,\(R_e\) es la distancia en equilibrio (es decir, la longitud del enlace de equilibrio),\(D_e\) es la energía de disociación de la molécula,\(k\) es una constante que mide la fuerza del enlace, y\(V\) es la energía potencial. Obsérvese que\(R_e\) es la distancia a la que la energía potencial es mínima, y por eso llamamos a esto la distancia de equilibrio. Tendríamos que aplicar energía para separar aún más los átomos, o para acercarlos más (Figura\(\PageIndex{2}\)).
A temperatura ambiente, hay suficiente energía térmica para inducir pequeñas vibraciones que desplazan a los átomos de sus posiciones de equilibrio, pero para moléculas estables, el desplazamiento es muy pequeño:\(R-R_e\rightarrow0\). En el siguiente ejemplo probaremos que bajo estas condiciones, el potencial parece una parábola, o en términos matemáticos,\(V(R)\) es proporcional al cuadrado del desplazamiento. Este tipo de potencial se denomina 'potencial armónico'. Se dice que una vibración es armónica simple si el potencial es proporcional al cuadrado del desplazamiento (como en los simples problemas de resorte que puede haber estudiado en física).
Ejemplo\(\PageIndex{1}\)
Expandir el potencial Morse como una serie de potencias y demostrar que las vibraciones de la molécula son aproximadamente armónicas simples si el desplazamiento\(R-R_e\) es pequeño.
Solución
La variable relevante en este problema es el desplazamiento\(R-R_e\), no la distancia real\(R\). Llamemos al desplazamiento\(R-R_e=x\), y vamos a reescribir la ecuación\ ref {morse} como
\[\label{morse2}V(R)=D_e\left(1-e^{-kx}\right)^2\]
El objetivo es demostrar que\(V(R) =cx^2\) (es decir, el potencial es proporcional al cuadrado del desplazamiento) cuándo\(x\rightarrow0\). La constante\(c\) es la constante de proporcionalidad. Podemos abordar esto de dos maneras diferentes. Una opción es expandir la función mostrada en Ecuación\ ref {morse2} alrededor de cero. Esto sería correcto, pero pero implica algún trabajo innecesario. La variable\(x\) aparece solo en el término exponencial, por lo que una opción más simple es expandir la función exponencial, y tapar el resultado de esta expansión de nuevo en la Ecuación\ ref {morse2}. Veamos cómo funciona esto:
Queremos expandirnos\(e^{-kx}\) como\(a_0+a_1 x + a_2 x^2...a_n x^n\), y sabemos que los coeficientes son\(a_n=\frac{1}{n!} \left( \frac{d^n f(x)}{dx^n} \right)_0.\)
El coeficiente\(a_0\) es\(f(0)=1\). Los tres primeros derivados de\(f(x)=e^{-kx}\) son
- \(f'(x)=-ke^{-kx}\)
- \(f''(x)=k^2e^{-kx}\)
- \(f'''(x)=-k^3e^{-kx}\)
Cuando se evalúa en\(x=0\) obtenemos,\(-k, k^2, -k^3...\)
y por lo tanto\(a_n=\frac{(-1)^n k^n}{n!}\) para\(n=0, 1, 2...\).
Por lo tanto,
\[e^{-kx}=1-kx+k^2x^2/2!-k^3x^3/3!+k^4x^4/4!...\]
y
\[1-e^{-kx}=+kx-k^2x^2/2!+k^3x^3/3!-k^4x^4/4!...\]
Desde el último resultado, cuando\(x<<1\), sabemos que los términos en\(x^2, x^3...\) serán cada vez más pequeños, así\(1-e^{-kx}\approx kx\) y\((1-e^{-kx})^2\approx k^2x^2\).
Tapando este resultado en la Ecuación\ ref {morse2} obtenemos\(V(R) \approx D_e k^2 x^2\), por lo que demostramos que el potencial es proporcional al cuadrado del desplazamiento cuando el desplazamiento es pequeño (la constante de proporcionalidad es\(D_e k^2\)). Por lo tanto, ¡las moléculas diatómicas estables a temperatura ambiente se comportan prácticamente como una primavera! (No tomes esto demasiado literalmente. Como discutiremos más adelante, los resortes microscópicos no se comportan en absoluto como resortes macroscópicos).

