3.3: Serie Taylor

Antes de discutir más aplicaciones de la serie Maclaurin, ampliemos nuestra discusión al caso más general donde expandimos una función alrededor de valores diferentes a cero. Digamos que queremos expandir una función alrededor del número\(h\). Si\(h=0\), llamamos a la serie una serie de Maclaurin, y si\(h\neq0\) llamamos a la serie una serie de Taylor. Debido a que las series Maclaurin son un caso especial del caso más general, podemos llamar a todas las series series Taylor y omitir la distinción. Lo siguiente es cierto para una función\(f(x)\) siempre que la función y todas sus derivadas sean finitas en\(h\):

\[\label{taylor} f(x)=a_0 + a_1(x-h)+a_2(x-h)^2+...+a_n(x-h)^n = \displaystyle\sum_{n=0}^{\infty}a_n(x-h)^n\]

Los coeficientes se calculan como

\[\label{taylorcoeff} a_n=\frac{1}{n!}\left( \frac{d^n f}{dx^n}\right)_h\]

Observe que en lugar de evaluar la función y sus derivadas en ahora las\(x=0\) evaluamos en\(x=h\), y que el conjunto de bases es ahora\(1, (x-h), (x-h)^2,...,(x-h)^n\) en lugar de\(1, x, x^2,...,x^n\). Una serie Taylor será una buena aproximación de la función a valores\(x\) cercanos a\(h\), de la misma manera que las series Maclaurin proporcionan buenas aproximaciones cercanas a cero.

Para ver cómo funciona esto volvamos a la función exponencial. Recordemos que la expansión Maclaurin de\(e^x\) se muestra en la Ecuación\(3.1.3\). Sabemos lo que pasa si nos expandimos alrededor de cero, así que para practicar, vamos a expandirnos alrededor\(h=1\). El coeficiente\(a_0\) es\(f(1)= e^1=e\). Todos los derivados son\(e^x\), por lo\(f'(1)=f''(1)=f'''(1)...=e.\) tanto,\(a_n=\frac{e}{n!}\) y la serie es por lo tanto

\[\label{taylorexp} e\left[ 1+(x-1)+\frac{1}{2}(x-1)^2+\frac{1}{6}(x-1)^3+... \right]=\displaystyle\sum_{n=0}^{\infty}\frac{e}{n!}(x-1)^n\]

Podemos usar los mismos argumentos que usamos antes para concluir que\(e^x\approx ex\) si\(x\approx 1\). Si\(x\approx 1\),\((x-1)\approx 0\), y los términos\((x-1)^2, (x-1)^3\) serán cada vez más pequeños y contribuirán cada vez menos a la suma. Por lo tanto,

\[e^x \approx e \left[ 1+(x-1) \right]=ex.\]

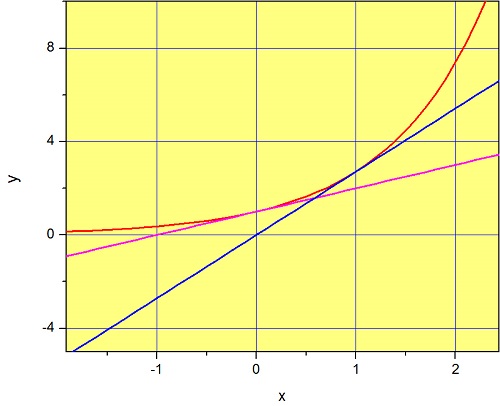
Esta es la ecuación de una línea recta con pendiente\(e\) e\(y\) -intercepción 0. De hecho, a partir de Ecuación\(3.1.7\) podemos ver que todas las funciones mirarán lineales a valores cercanos a\(h\). Esto se ilustra en la Figura\(\PageIndex{1}\), que muestra la función exponencial (rojo) junto con las funciones\(1+x\) (magenta) y\(ex\) (azul). No es sorprendente que la función\(1+x\) proporcione una buena aproximación de\(e^x\) valores cercanos a cero (ver Ecuación\(3.1.3\)) y la función\(ex\) proporciona una buena aproximación alrededor\(x=1\) (Ecuación\ ref {taylorexp}).

Figura\(\PageIndex{1}\): Dos aproximaciones lineales de la función exponencial. La función\(e^x\) se traza en rojo junto con la función\(y = 1+x\) (magenta) y\(y=ex\) (azul). (CC BY-NC-SA; Marcia Levitus)

Ejemplo\(\PageIndex{1}\):

Ampliar\(f(x)=\ln{x}\) acerca de\(x=1\)

Solución

\[f(x)=a_0 + a_1(x-h)+a_2(x-h)^2+...+a_n(x-h)^n, a_n=\frac{1}{n!}\left( \frac{d^n f}{dx^n}\right)_h \nonumber\]

\[a_0=f(1)=\ln(1)=0 \nonumber\]

Los derivados de\(\ln{x}\) son:

\[f'(x) = 1/x, f''(x)=-1/x^2, f'''(x) = 2/x^3, f^{(4)}(x)=-6/x^4, f^{(5)}(x)=24/x^5... \nonumber\]

y por lo tanto,

\[f'(1) = 1, f''(1)=-1, f'''(1) = 2, f^{(4)}(1)=-6, f^{(5)}(1)=24.... \nonumber\]

Para calcular los coeficientes, necesitamos dividir por\(n!\):

• \(a_1=f'(1)/1!=1\)
• \(a_2=f''(1)/2!=-1/2\)
• \(a_3=f'''(1)/3!=2/3!=1/3\)
• \(a_4=f^{(4)}(1)/4!=-6/4!=-1/4\)
• \(a_n=(-1)^{n+1}/n\)

Por lo tanto, la serie es:

\[f(x)=0 + 1(x-1)-1/2 (x-1)^2+1/3 (x-1)^3...=\displaystyle{\color{Maroon}\displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n}(x-1)^{n}} \nonumber\]

Tenga en cuenta que iniciamos la suma en\(n=1\) porque\(a_0=0\), por lo que el término para\(n=0\) no tiene ninguna contribución.

¿Necesitas ayuda? Los enlaces a continuación contienen ejemplos resueltos.

Enlaces externos:

Encontrar la serie Taylor de una función I: http://patrickjmt.com/taylor-and-maclaurin-series-example-2/