4.1: Definiciones y conceptos generales
- Page ID
- 69908
Una ecuación diferencial es una ecuación que define una relación entre una función y una o más derivadas de esa función.
Por ejemplo, esta es una ecuación diferencial que relaciona la función\(y(t)\) con sus derivadas primera y segunda:
\[\dfrac{d^2}{dt^2}y(t)+\dfrac{1}{4}\dfrac{d}{dt}y(t)+y(t)=\sin(t) \nonumber\]
El ejemplo anterior es una ecuación diferencial ordinaria (ODE) porque la función desconocida,\(y(t)\), es una función de una sola variable (en este caso\(t\)). Debido a que estamos tratando con una función de una sola variable, en la ecuación sólo aparecen las derivadas ordinarias. Si tratáramos de una función de dos o más variables, las derivadas parciales de la función aparecerían en la ecuación, y llamaríamos a esta ecuación diferencial una ecuación diferencial parcial (PDE). A continuación se muestra un ejemplo de una PDE. Discutiremos las PDEs hacia el final del semestre.
\[\dfrac{\partial ^2u}{\partial x^2}+\dfrac{\partial ^2u}{\partial y^2}+\dfrac{\partial ^2u}{\partial z^2}=c^2 \dfrac{\partial ^2u}{\partial t^2} \nonumber\]
Tenga en cuenta que en el ejemplo anterior nos pusimos 'perezosos' y usamos\(u\) en lugar de\(u(x,y,z,t)\). El hecho de que\(u\) es una función de\(x,y,z\), y\(t\) es obvio a partir de las derivadas, por lo que verás que muchas veces nos relajaremos y no escribiremos las variables explícitamente con la función.
¿Por qué necesitamos estudiar ecuaciones diferenciales? La respuesta es simple: Las ecuaciones diferenciales surgen en los modelos matemáticos que describen la mayoría de los procesos físicos. La figura\(\PageIndex{1}\) ilustra tres ejemplos.
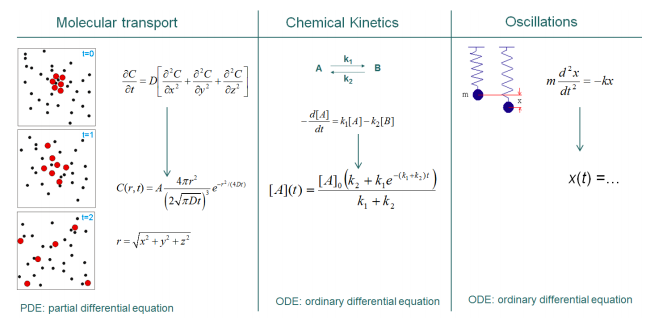
La primera columna ilustra el problema del transporte molecular (difusión). Supongamos que los círculos rojos representan moléculas de sacarosa (azúcar) y las moléculas de círculos negros de agua, y supongamos que está interesado en modelar la concentración de sacarosa en función de la posición y el tiempo después de disolver algo de sacarosa justo en el medio del recipiente. La ecuación diferencial que describe el proceso es una ecuación diferencial parcial porque la concentración será una función de dos variables:\(r\), la distancia desde el origen, y\(t\), el tiempo transcurrido desde el momento en que iniciaste el experimento. La solución mostrada en la figura se obtuvo asumiendo que todas las moléculas de sacarosa se concentran en el centro en el tiempo cero. Se podría resolver la ecuación diferencial con otras condiciones iniciales.
La segunda columna ilustra un sistema químico donde un compuesto A reacciona para dar B. La reacción es reversible, y podría, por ejemplo, representar dos isómeros diferentes de una misma molécula. La ecuación diferencial modela cómo la concentración de A, [A], cambia con el tiempo. De hecho, analizaremos este problema en detalle y encontraremos la solución que se muestra en la figura. Como veremos, en este caso también estamos asumiendo ciertas condiciones iniciales.
Finalmente, la tercera columna ilustra una masa unida a un resorte. También analizaremos esta ecuación, y no se muestra la solución porque será tu trabajo conseguirlo en tu tarea. Se puede pensar que esto es un problema de física, pero debido a que las moléculas tienen enlaces químicos, y los átomos vibran alrededor de sus posiciones de equilibrio, sistemas como estos también son de interés para los químicos.
Resolver la ecuación diferencial significa encontrar la función (o familia de funciones) que satisface la ecuación. En nuestro primer ejemplo en Figura\(\PageIndex{1}\), necesitaríamos encontrar la función C\((r,t)\) que satisfaga la ecuación. En el segundo ejemplo necesitaríamos encontrar todas las funciones A\((t)\) que satisfagan la ecuación. Como veremos en breve, si la solución es una función o una familia de funciones depende de si estamos restringidos por condiciones iniciales (por ejemplo, en el tiempo cero [B] = 0) o no.
El orden de una ecuación diferencial (parcial u ordinaria) es la derivada más alta que aparece en la ecuación. A continuación se muestra un ejemplo de una ecuación diferencial ordinaria de primer orden:
\[\label{eq1}\dfrac{dy}{dx}+3y=8e^x\]
En este ejemplo, estamos buscando todas las funciones\(y(x)\) que satisfagan la ecuación\ ref {eq1}. Como es habitual, llamaremos a\(x\) la variable independiente, y a\(y\) la variable dependiente. De nuevo,\(y\) es por supuesto\(y(x)\), pero muchas veces no escribimos esto explícitamente para ahorrar espacio y tiempo. Esta es una ecuación diferencial ordinaria porque\(y\) es una función de una sola variable. Es una ecuación diferencial de primer orden porque la derivada más alta es de primer orden. También es una ecuación diferencial lineal porque la variable dependiente y todas sus derivadas aparecen de manera lineal. La distinción entre ODEs lineales y no lineales es muy importante porque existen diferentes métodos para resolver diferentes tipos de ecuaciones diferenciales. Matemáticamente, una ODE lineal de primer orden tendrá esta forma general:
\[\dfrac{dy}{dx}+f_1(x) y=f_2(x)\]
Es crucial entender que la linealidad se refiere a los términos que incluyen la variable dependiente (en este caso\(y\)). Los términos que involucran\(x\) (\(f_1(x)\)y\(f_2(x)\)) pueden ser no lineales, como en la Ecuación\ ref {eq1}. A continuación se muestra un ejemplo de una ecuación diferencial no lineal. Obsérvese que la variable dependiente aparece en una función trascendental (en este caso exponencial), y eso hace que esta ecuación no sea lineal:
\[\dfrac{dy}{dx}+3e^y=8x \nonumber\]
Análogamente, una ODE lineal de segundo orden tendrá la forma general:
\[\label{eq:linear}\dfrac{d^2y}{dx^2}+f_1(x)\dfrac{dy}{dx}+f_2(x) y=f_3(x)\]
Nuevamente, no nos importa si las funciones\(f_1(x), f_2(x)\) y\(f_3(x)\) son lineales en\(x\) o no. Lo único que importa es que los términos que involucran a la variable dependiente son.
Identificar las variables dependientes e independientes: Ponte a prueba con este breve cuestionario. http://tinyurl.com/ll22wnv
¿Lineal o no lineal? Consulta si puedes identificar las ODEs lineales en este breve cuestionario. http://tinyurl.com/msldkp3
Todavía estamos definiendo conceptos, ¡pero hasta ahora no hemos dicho nada con respecto a cómo resolver ecuaciones diferenciales! Todavía tenemos que repasar algunas cosas más, así que ten paciencia.
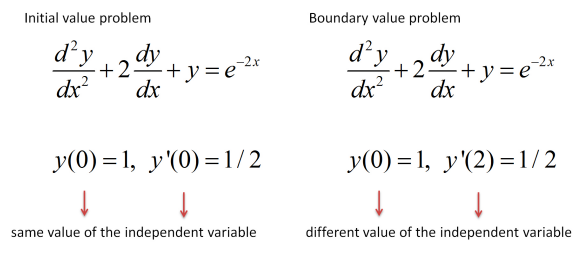
Una ecuación diferencial de\(nth\) orden -junto con condiciones\(n\) auxiliares impuestas al mismo valor de la variable independiente se denomina problema de valor inicial. Por ejemplo, nos puede interesar encontrar la función\(y(x)\) que satisfaga las siguientes condiciones:
\[\label{eq2}y''=e^{-x}, y(0)=1, y'(0)=4\]
Observe que estamos introduciendo diferentes tipos de notaciones para que se acostumbre a ver ecuaciones matemáticas en diferentes 'sabores'. Aquí, por\(y''\) supuesto, significa\(\dfrac{d^2y(x)}{dx^2}\). Este es un problema de valor inicial porque tenemos una ecuación diferencial de segundo orden con dos condiciones auxiliares impuestas al mismo valor de\(x\) (en este caso\(x=0\)). Hay infinitas funciones\(y(x)\) que satisfacen\(y''=e^{-x}\), pero sólo una satisfará también las dos condiciones iniciales que impusimos. Si estuviéramos tratando con una ecuación diferencial de primer orden necesitaríamos solo una condición inicial. Necesitaríamos tres para una ecuación diferencial de tercer orden.
¿Cómo utilizamos las condiciones iniciales para encontrar una solución? En general, la solución de una ODE de segundo orden contendrá dos constantes arbitrarias (en el ejemplo siguiente\(c_1\) y\(c_2\)). Esto es lo que llamaremos la solución general de la ecuación diferencial. Por ejemplo,
\(y(x)=e^{-x} + c_1 x+c_2\)es la solución general de\(y''=e^{-x}\). Podemos verificar que esto es cierto tomando la segunda derivada de esta función. Nuevamente, aún no sabemos cómo obtener estas soluciones, pero si se nos da esta solución, sabemos cómo verificar si es correcta. Es claro que\(c_1\) y\(c_2\) puede ser en principio cualquier cosa, por lo que la solución de la ODE es toda una familia de funciones. No obstante, si se nos dan condiciones iniciales estamos buscando una solución particular, una que no sólo satisfaga la ODE, sino también las condiciones iniciales. ¿Qué función es esa?
La primera condición inicial establece que\(y(0)=1\). Por lo tanto,
\[y(x)=e^{-x} + c_1 x+c_2\Rightarrow y(0)=1+c_2 \nonumber\]
\[y(0)=1 \Rightarrow 1=1+c_2 \Rightarrow c_2 =0 \nonumber\]
Hasta el momento, demostramos que las funciones\(y(x)=e^{-x} + c_1 x\) satisfacen no sólo la ODE, sino también la condición inicial\(y(0)=1\). Todavía tenemos otra condición inicial, que nos permitirá determinar el valor de\(c_1\).
\[y'(x)=-e^{-x} + c_1\Rightarrow y'(0)=-1+c_1 \nonumber\]
\[y'(0)=4 \Rightarrow 4=-1+c_1 \Rightarrow c_1 =5 \nonumber\]
Por lo tanto, la función\(y(x)=e^{-x}+5x\) es la solución particular del problema del valor inicial descrito en la Ecuación\ ref {eq2}. Podemos verificar nuestra respuesta verificando que esta solución satisface las tres ecuaciones del problema del valor inicial:
- \(y''=e^{-x} \rightarrow\)\(\dfrac{d^2}{dx^2} (e^{-x}+5x)=e^{-x}\), por lo que sabemos que la solución que encontramos satisface la ecuación diferencial.
- \(y(0)=1 \rightarrow\)e\(^{-0}+5\times 0=1\), por lo que sabemos que la solución que encontramos satisface una de las condiciones iniciales.
- \(y'(0)=4 \rightarrow\)\(\dfrac{d}{dx} (e^{-x}+5x)=-e^{-x}+5\Rightarrow y'(0)=4\), por lo que sabemos que la solución que encontramos satisface también la otra condición inicial.
Por lo tanto, demostramos que efectivamente esa\(y(x)=e^{-x}+5x\) es la solución del problema.
Una ecuación diferencial de\(nth\) orden -junto con condiciones\(n\) auxiliares impuestas a más de un valor de la variable independiente se denomina problema de valor límite. ¿Cuál es la diferencia entre un problema de valor límite y un problema de valor inicial? En el primer caso, las condiciones se imponen a diferentes valores de la variable independiente, mientras que en el segundo caso, como acabamos de ver, las condiciones se imponen al mismo valor de la variable independiente. Por ejemplo, esto sería un problema de valor límite:
\[\label{eq3}y''=e^{-x}, y(0)=1, y(1)=0\]
Observe que aún tenemos dos condiciones porque nos encontramos ante una ecuación diferencial de segundo orden. Sin embargo, una condición trata\(x=1\) y la otra con\(x=0\). Las condiciones pueden referirse a valores de la primera derivada, como en el ejemplo anterior, o a valores de la propia función, como en el ejemplo de Ecuación\ ref {eq3}.
¿Por qué necesitamos distinguir entre el valor inicial y los problemas de valor límite? La razón radica en un teorema que establece que, para las ODEs lineales, la solución de un problema de valor inicial existe y es única, pero un problema de valor límite no tiene la garantía de existencia y singularidad. El teorema no es tan sencillo (por ejemplo requiere que las funciones en\(x\) (\(f_{1...3}\)en la Ecuación\ ref {eq:lineal}) sean continuas), pero la conclusión es que podemos encontrar una solución siempre que las condiciones se impongan al mismo valor de\(x\), pero puede que no encontremos una solución siempre que el las condiciones se imponen a diferentes valores. Veremos ejemplos cuando discutamos las ODE de segundo orden, y en particular discutiremos cómo las condiciones límite dan lugar a fenómenos físicos interesantes. Por ejemplo, veremos que las condiciones límite son las responsables de que se cuantifiquen las energías en átomos y moléculas.
Volviendo al problema del valor límite de la Ecuación\ ref {eq3}, es importante reconocer que debido a que la ecuación diferencial real es la misma que en el ejemplo de la Ecuación\ ref {eq2}, la solución general sigue siendo la misma:\(y(x)=e^{-x} + c_1 x+c_2\). Sin embargo, la solución particular será diferente (diferentes valores de\(c_1\) y\(c_2\)), porque necesitamos satisfacer diferentes condiciones.
Como en el primer ejemplo, la primera condición de límite establece que\(y(0)=1\) así:
\[y(x)=e^{-x} + c_1 x+c_2\Rightarrow y(0)=1+c_2 \nonumber\]
\[y(0)=1 \Rightarrow 1=1+c_2 \Rightarrow c_2 =0 \nonumber\]
como antes. Sin embargo, ahora
\[y(1)=e^{-1} + c_1 \nonumber\]
donde hemos usado el resultado\(c_2=0\) por lo
\[y(1)=0 \Rightarrow 0=e^{-1}+c_1 \Rightarrow c_1 =-e^{-1} \nonumber\]
y la solución particular es, por lo tanto\(y(x)=e^{-x}-e^{-1}x\). Como hicimos antes, es importante que revisemos nuestra solución. Si tenemos razón, esta solución necesita satisfacer todas las relaciones establecidas en la Ecuación\ ref {eq3}.
- \(y''=e^{-x} \rightarrow\)\(\dfrac{d^2}{dx^2} (e^{-x}-e^{-1}x)=e^{-x}\), por lo que la solución satisface la ecuación diferencial.
- \(y(0)=1 \rightarrow\)e\(^{-0}-e^{-1}\times 0=1\), por lo que nuestra solución satisface una de las condiciones límite.
- \(y(1)=0 \rightarrow\)\(e^{-1}-e^{-1}\times1=0\), por lo que nuestra solución satisface también la otra condición de límite.
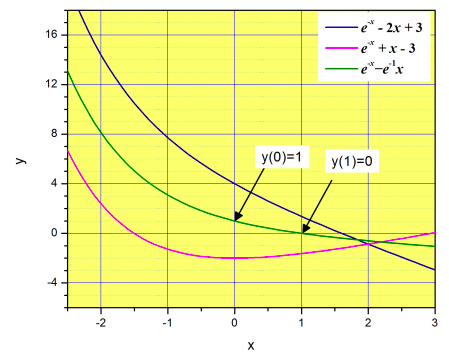
La figura\(\PageIndex{3}\) ilustra la diferencia entre la solución general y la solución particular. La solución general tiene dos constantes arbitrarias, por lo que hay un número infinito de funciones que satisfacen la ecuación diferencial. Se muestran tres ejemplos en diferentes colores. Sin embargo, solo una de estas satisface ambas condiciones de contorno (se muestra con las flechas).
Usando condiciones de límite: vea si puede obtener la solución particular de una ODE de segundo orden en este breve cuestionario. http://tinyurl.com/lovh4x3
Hasta el momento hemos discutido cómo:
- Identificar las variables dependientes e independientes
- Identificar el orden de la ecuación diferencial.
- Identificar si la ecuación es lineal o no
- Utilizar condiciones iniciales o límite para obtener soluciones particulares a partir de soluciones generales
- Comprueba tus resultados para asegurarte de que cumples con la ecuación diferencial y todas las condiciones iniciales o límite
Obviamente nos falta la pregunta más importante: ¿Cómo resolvemos la ecuación diferencial? Desafortunadamente, no existe un método universal, y de hecho algunas ecuaciones diferenciales no pueden resolverse analíticamente. Veremos algunos ejemplos de ecuaciones que no se pueden resolver analíticamente y discutiremos qué se puede hacer en esos casos. En esta clase solo discutiremos algunas ecuaciones diferenciales de interés en la química física. No es nuestra intención cubrir el tema de manera integral, y no tocaremos otras ecuaciones diferenciales que puedan ser de interés en otras disciplinas. Sin embargo, los antecedentes que obtendrás en esta clase te permitirán enseñarte temas más avanzados en ecuaciones diferenciales si tu futura carrera exige que tengas un conocimiento más profundo de la materia.

