4.3: Cinética química

El término cinética química se refiere al estudio de las tasas de reacciones químicas. Como veremos, las ecuaciones diferenciales juegan un papel central en el tratamiento matemático de la cinética química. Comenzaremos con los ejemplos más simples, y luego pasaremos a casos más complejos. Como verán, en esta sección nos centraremos en un par de mecanismos de reacción. El tema común será encontrar expresiones que nos permitan calcular la concentración de las diferentes especies que forman parte de la reacción en diferentes tiempos de reacción.

Empecemos por el caso más sencillo, en el que un reactivo A reacciona para dar el producto B. Supondremos que la reacción procede en un solo paso, es decir, no hay intermedios que puedan detectarse.

\[\label{1order} A \overset{k}{\rightarrow}B\]

Usaremos la siguiente notación para las concentraciones dependientes del tiempo de A y B: [A]\((t)\), [B]\((t)\), o simplemente [A] y [B]. Usaremos [A]\(_0\) y [B]\(_0\) para denotar las concentraciones de A y B en el momento\(t=0\). La constante\(k\) es la constante de velocidad de la reacción, y es una medida de cuán rápida o lenta es la reacción. Depende de la reacción en sí (los compuestos químicos A y B) y de factores ambientales como la temperatura. La constante de velocidad no depende de las concentraciones de las especies involucradas en la reacción. Las unidades de\(k\) dependen del mecanismo particular de la reacción, como veremos a través de los ejemplos. Para el caso descrito anteriormente, las unidades serán 1/tiempo (e.g.\(s^{-1}\))

La velocidad de la reacción (\(r\)) se definirá como el número de moles de A que desaparecen o el número de moles de B que aparecen por unidad de tiempo (por ejemplo, por segundo) y volumen (por ejemplo, litro). Esto es cierto por la estequiometría de la reacción, como discutiremos en un momento. No obstante, debido a que la tasa es una cantidad positiva, usaremos un signo negativo si observamos la desaparición de A:

\[r=-\frac{d[A]}{dt}=\frac{d[B]}{dt}\]

La velocidad de reacción, por lo tanto, es una cantidad positiva con unidades de M.s\(^{-1}\), o en general, concentración por unidad de tiempo. Como veremos, la velocidad de la reacción depende de la concentración real del reactivo, y por lo tanto disminuirá en general a medida que la reacción avance y el reactante se convierta en producto. Aunque todas las moléculas de A son idénticas, no necesitan reaccionar al mismo instante. Considere el mecanismo simple de la Ecuación\ ref {1order}, e imagine que cada molécula de A tiene una probabilidad\(p = 0.001\) de reaccionar en cada intervalo de un segundo. Supongamos que comienzas con 1 mol de A en un matraz de 1 L (\([A]_0 = 1 M\)), y mides la concentración de A un segundo después. ¿Cuántos moles de A esperas ver? Para responder a esta pregunta, puedes imaginar que consigues que todos en China (alrededor de mil millones de personas) lancen un dado al mismo tiempo, y que todos los que obtengan un seis ganen el juego. ¿Cuántos ganadores esperas ver? Ya sabes que la probabilidad de que cada individuo obtenga un seis es\(p=1/6\), y por lo tanto una sexta parte de los jugadores ganará en una ronda del juego. Por lo tanto, se puede predecir que el número de ganadores será\(10^9/6\), y el número de perdedores será\(5/6\times10^9\). Si conseguimos que los perdedores jueguen una segunda ronda, esperamos que una sexta parte de ellos obtenga un seis, lo que da cuenta de la\(5/6\times10^9\times 1/6\) gente. Después de la segunda carrera, por lo tanto, todavía tendremos\((5/6)^2\times10^9\) perdedores.

Siguiendo la misma lógica, la probabilidad de que una molécula de A reaccione para dar B en cada intervalo de un segundo es\(= 1/1000\), y por lo tanto en el primer segundo se espera que\(6\times10^{23}/1000\) las moléculas reaccionen y\(999\times6\times10^{23}/1000\) permanezcan sin reaccionar. Es decir, durante el primer segundo de su reacción 0.001 moles de A se convirtieron en B, y por lo tanto la velocidad de la reacción fue\(10^{-3}Ms^{-1}\). Durante el segundo intervalo de un segundo de la reacción se espera que mil de las moléculas restantes reaccionen, y así sucesivamente. Imagina que vuelves una hora después (3,600 s). Esperamos que\((999/1000)^{3,600}\times 6\times10^{23}\) las moléculas permanezcan sin reaccionar, que se trata de\(1.6\times 10^{22}\) moléculas. Si se mide la velocidad de reacción en el siguiente segundo, se espera que mil de ellos (\(1.6\times 10^{19}\)moléculas, o\(2.7\times 10^{-5}\) moles) reaccionen para dar B. La velocidad de la reacción, por lo tanto, disminuyó de\(10^{-3}Ms^{-1}\) at\(t=1s\) a\(2.7\times10^{-5}Ms^{-1}\) at\(t = 1h\). Debes notar que la fracción de moléculas de A que reaccionan en cada segundo es siempre la misma (en este caso mil). Por lo tanto, el número de moléculas que reaccionan por intervalo de tiempo es proporcional al número de moléculas de A que permanecen sin reaccionar en un momento dado. Acabamos de concluir que la velocidad de reacción es proporcional a la concentración de A:

\[\label{eq:1st} r=-\frac{d[A]}{dt}=\frac{d[B]}{dt}=k[A]\]

La constante de proporcionalidad,\(k\), está relacionada con la probabilidad de que una molécula reaccione en un pequeño intervalo de tiempo, como se discutió anteriormente. En esta clase, nos concentraremos en resolver ecuaciones diferenciales como la anterior. Esta es una ecuación diferencial muy simple que se puede resolver usando diferentes condiciones iniciales. Digamos que nuestro objetivo es encontrar tanto [A]\((t)\) como [B]\((t)\). Como químicos, debemos tener en cuenta que la ley de conservación masiva requiere que

\[\label{mass} [A](t) + [B](t) = [A]_0 + [B]_0\]

En inglés sencillo, las concentraciones de A y B en cualquier momento necesitan sumar la suma de las concentraciones iniciales, ya que una molécula de A se convierte en B, y no podemos crear ni destruir materia. Nuevamente, hay que tener en cuenta que esta ecuación necesitará ser modificada de acuerdo a la estequiometría de la reacción. Llamaremos a una ecuación de este tipo un 'balance de masas'.

Antes de resolver esta ecuación, veamos otros ejemplos. ¿Cuáles son las ecuaciones diferenciales que describen este mecanismo secuencial?

\[A \overset{k_1}{\rightarrow}B\overset{k_2}{\rightarrow}C \nonumber\]

En este mecanismo, A se convierte en C a través de un intermedio, B. Todo lo que discutimos hasta ahora se aplicará a cada una de estas dos reacciones elementales (las dos que conforman el mecanismo general). Desde el punto de vista de A nada cambia. Debido a que la tasa de la primera reacción no depende de B, es irrelevante que B se convierta en C (imagina que le das 1 dólar al día a un amigo. No importa si tu amigo ahorra el dinero o se lo da a otra persona, aún pierdes 1 dólar por día).

\[\label{cons1} \frac{d[A]}{dt}=-k_1[A]\]

Por otro lado, la tasa de cambio de [B],\(d[B]/dt\) es la suma de la tasa a la que se crea B (\(k_1[A]\)), menos la velocidad a la que desaparece al reaccionar en C (\(k_2[B]\)):

\[\frac{d[B]}{dt}=k_1[A]-k_2[B] \label{cons2}\]

Esto se puede leer: La velocidad de cambio de [B] es igual a la velocidad a la que [B] aparece de A a B, menos la velocidad a la que [B] desaparece de B a C. En cada término, la velocidad es proporcional al reactivo de la etapa correspondiente: A para la primera reacción y B para la segunda etapa.

¿Y qué pasa con C? Nuevamente, es irrelevante que B se haya creado a partir de A (si obtienes 1 dólar al día de tu amiga, no te importa si ella lo obtuvo de sus padres, aún obtienes 1 dólar por día). La velocidad a la que aparece C es proporcional al reactivo en la segunda etapa: B. Por lo tanto:

\[\frac{d[C]}{dt}=k_2[B] \label{cons3}\]

Las tres últimas ecuaciones forman un sistema de ecuaciones diferenciales que deben resolverse considerando las condiciones iniciales del problema (por ejemplo, inicialmente tenemos A pero no B o C). Vamos a resolver este problema en un momento, pero aún necesitamos discutir algunos temas relacionados con la forma en que escribimos las ecuaciones diferenciales que describen un mecanismo en particular. Imagina que nos interesa

\[2 A + B \overset{k}{\rightarrow}3 C \nonumber\]

Sabemos que la velocidad de una reacción se define como el cambio en la concentración con el tiempo... pero ¿qué concentración? ¿lo es\(d[A]/dt\)? o\(d[B]/dt\)? o\(d[C]/dt\)? Todos estos son diferentes porque se crean 3 moléculas de C cada vez que desaparecen 1 de B y 2 de A. ¿Cuál debemos usar? Porque 2 de A desaparecen cada vez que 1 de B desaparece:\(d[A]/dt= 2 d[B]/dt\). Ahora bien, considerando que las tasas son cantidades positivas, y que los derivados para los reactivos,\(d[A]/dt\) y\(d[B]/dt\), son negativos:

\[r=-\frac{1}{2}\frac{d[A]}{dt}=-\frac{d[B]}{dt}=\frac{1}{3}\frac{d[C]}{dt}\]

Este ejemplo muestra cómo lidiar con los coeficientes estequiométricos de la reacción. Obsérvese que en todos nuestros ejemplos asumimos que las reacciones proceden tal y como están escritas, sin ningún paso intermedio 'oculto'.

Reacciones de primer orden

Hemos cubierto suficientes antecedentes, para que podamos comenzar a resolver los mecanismos que introdujimos. Empecemos por la más fácil (Ecuaciones\ ref {1order},\ ref {eq:1st} y\ ref {mass}):

\[A \overset{k}{\rightarrow}B \nonumber\]

\[r=-\frac{d[A]}{dt}=\frac{d[B]}{dt}=k[A] \nonumber\]

\[[A](t) + [B](t) = [A]_0 + [B]_0 \nonumber\]

Este mecanismo se denomina reacción de primer orden debido a que la velocidad es proporcional a la primera potencia de la concentración de reactivo. Para una reacción de segundo orden, la velocidad es proporcional al cuadrado de la concentración de reactivo (ver Problema\(4.3\)). Empecemos por encontrar\([A](t)\) de\(-\frac{d[A]}{dt}=k[A]\). Luego obtendremos\([B](t)\) del balance de masas. Esta es una ecuación diferencial muy simple porque es separable:

\[-\frac{d[A]}{dt}=k[A] \nonumber\]

\[\frac{d[A]}{[A]}=-kdt \nonumber\]

Integramos ambos lados de la ecuación, y combinamos las dos constantes de integración en una:

\[\ln{[A]}=-kt+c \nonumber\]

Tenemos que resolver para [A]:

\[[A]=e^{-kt+c}=e^ce^{-kt}=c_2e^{-kt} \nonumber\]

Esta es la solución general del problema. Supongamos que estamos dando las siguientes condiciones iniciales: [A]\((t=0)=[A]_0\), [B]\((t=0)=0.\) Usaremos esta información para encontrar la constante arbitraria\(c_2\):

\[[A](t=0)=c_2e^{0}=c_2 \nonumber\]

Por lo tanto, la solución particular es:

\[\label{eq:mdecay} [A](t)=[A]_0e^{-kt}\]

¿Y qué pasa con [B]? Del balance de masas, [B] = [A]\(_0\) + [B]\(_0\) - [A] = [A]\(_0\) - [A]\(_0e^{-kt}= [A]_0\left(1-e^{-kt}\right)]\).

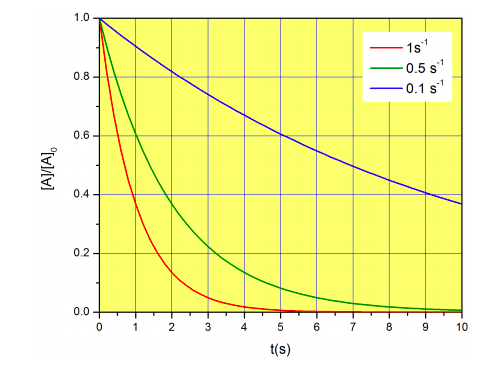
La figura\(\PageIndex{4}\) muestra tres ejemplos de decae con diferentes constantes de velocidad.

Podemos calcular la vida media de la reacción (\(t_{1/2}\)), definida como el tiempo requerido para que la mitad de la concentración inicial de A reaccione. De la ecuación\ ref {eq:mdecay}:

\[\frac{[A](t)}{[A]_0}=e^{-kt} \nonumber\]

Figura\(\PageIndex{4}\): Concentración dependiente del tiempo del reactivo en la reacción\(A \overset{k}{\rightarrow} B\) (CC BY-NC-SA; Marcia Levitus)

Cuando\(t=t_{1/2}\),

\[\frac{1}{2}=e^{-kt_{1/2}} \nonumber\]

\[\ln{1/2}=-kt_{1/2}\rightarrow \ln{2}=kt_{1/2} \nonumber\]

\[t_{1/2}=\frac{\ln{2}}{k} \nonumber\]

Obsérvese que en este caso, la vida media no depende de la concentración inicial de A. Esto no será el caso de otros tipos de mecanismos. Además, observe que ya hemos cubierto el concepto de vida media en el Capítulo 1 (ver Figura\(1.3.1\)), por lo que este podría ser un buen momento para volver a leer esa sección y refrescar lo que ya hemos aprendido sobre el bosquejo de decae exponencial.

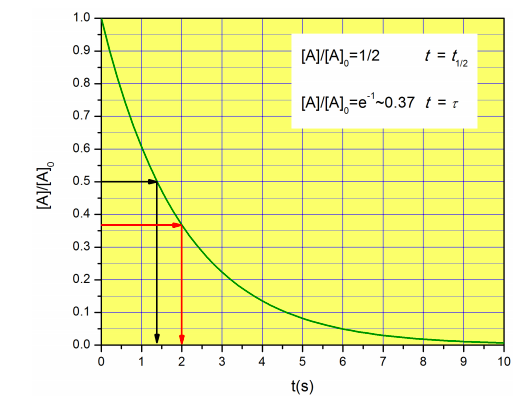
En la química física, los científicos suelen hablar del 'tiempo de relajación' en lugar de la vida media. El tiempo de relajación\(\tau\) para una decadencia de la forma\(a^{-b t}\) es\(1/b\), así que en este caso, el tiempo de relajación es simplemente\(1/k\). Observe que el tiempo de relajación tiene unidades de tiempo, y representa el tiempo en el que la concentración ha decaído a\(e^{-1}\) de su valor original:

\[[A]=[A]_0e^{-t/\tau}\rightarrow \frac{[A]}{[A]_0}=e^{-t/\tau} \xrightarrow{t=\tau}\frac{[A]}{[A]_0}=e^{-1}\approx0.37 \nonumber\]

La semivida y el tiempo de relajación se comparan en la Figura\(\PageIndex{5}\) para una reacción con\(k=0.5 s^{-1}\).

Figura\(\PageIndex{5}\): Semivida (negro) y tiempo de relajación (rojo) para la reacción\(A \overset{k}{\rightarrow} B\) con\(k = 0.5s^{−1}\) (CC BY-NC-SA; Marcia Levitus)

Procesos consecutivos de primer orden

Ahora analizaremos un mecanismo más complejo, que implica la formación de una especie intermedia (B):

\[A \overset{k_1}{\rightarrow}B\overset{k_2}{\rightarrow}C \nonumber\]

que se describe matemáticamente por Ecuaciones\ ref {cons1},\ ref {cons2} y\ ref {cons3}. Supongamos que inicialmente la concentración de A es [A]\(_0\), y las concentraciones de B y C son cero. Además, podemos escribir un balance de masas, que para estas condiciones iniciales se expresa como:

\[[A](t)+[B](t)+[C](t)=[A]_0 \nonumber\]

Resumimos las ecuaciones que tenemos:

\[\frac{d[A]}{dt}=-k_1[A]\label{consq1}\]\[\frac{d[B]}{dt}=k_1[A]-k_2[B]\label{consq2}\]\[\frac{d[C]}{dt}=k_2[B]\label{consq3}\]\[[A]+[B]+[C]=[A]_0\label{consq4}\]\[[A](t=0)=[A]_0\label{consq5}\]\[[B](t=0)=[C](t=0)=0\label{consq6}\]

Tenga en cuenta que la ecuación\ ref {consq4} no es independiente de las ecuaciones\ ref {consq1} -\ ref {consq3}. Si tomas la derivada de\ ref {consq4} obtienes\(d[A]/dt+d[B]/dt+d[C]/dt=0\), que es lo mismo que obtienes si agregas Ecuaciones\ ref {consq1} -\ ref {consq3}. Esto significa que las Ecuaciones\ ref {consq1} -\ ref {consq4} no son todas independientes, y tres de ellas son suficientes para que podamos resolver el problema. Como verás, el balance de masa (\ ref {consq4}) nos dará una manera muy fácil de resolver para [C] una vez que tengamos [A] y [B], así que lo usaremos en lugar de la Ecuación\ ref {consq3}.

Tenemos que resolver el sistema de Ecuaciones\ ref {consq1} -\ ref {consq6}, y aunque existen métodos para resolver sistemas de ecuaciones diferenciales (por ejemplo usando álgebra lineal), este es bastante fácil que se puede resolver con lo que hemos aprendido hasta ahora. Esto se debe a que no todas las ecuaciones contienen todas las variables. En particular, la Ecuación\ ref {consq1} es una ecuación simple separable con variable dependiente [A], que puede resolverse independientemente de [B] y [C]. De hecho, acabamos de resolver esta ecuación en la sección Reacciones de Primer Orden, así que escribamos el resultado:

\[\label{eq:a(t)} [A](t)=[A]_0e^{-k_1t}\]

La ecuación\ ref {consq2} contiene dos variables dependientes, pero afortunadamente acabamos de obtener una expresión para una de ellas. Ahora podemos reescribir\ ref {consq2} como:

\[\label{consq7} \frac{d[B]}{dt}=k_1[A]_0e^{-k_1t}-k_2[B]\]

La ecuación\ ref {consq7} contiene solo una variable dependiente, [B], una variable independiente\(t\), y tres constantes:\(k_1\),\(k_2\) y\([A]_0\). Por lo tanto, se trata de una ecuación diferencial ordinaria, y si es separable o lineal, podremos resolverla con las técnicas que aprendimos en este capítulo. Recordar eq. [sep], y verificar que la ecuación\ ref {consq7} no se puede separar como

\[\frac{d[B]}{dt}=\frac{g([B])}{h(t)} \nonumber\]

La ecuación\ ref {consq7} no es separable. ¿Es lineal? Recuérdese la ecuación\ ref {lineal} y verifique si puede escribir esta ecuación como\(\frac{d[B]}{dt}+p(t) [B]=q(t)\). De hecho, podemos:

\[\label{consq8} \frac{d[B]}{dt}+k_2[B]=k_1[A]_0e^{-k_1t}\]

Usemos la lista de pasos delineados en la Sección 4.2. Tenemos que calcular el factor integrador\(e^{ \int p(x)dx }\), que en este caso lo es\(e^{ \int k_2dt }=e^{k_2t}\). Luego multiplicamos la ecuación\ ref {consq8} por el factor integrador:

\[\frac{d[B]}{dt}e^{k_2t}+k_2[B]e^{k_2t}=k_1[A]_0e^{-k_1t}e^{k_2t}=k_1[A]_0e^{(k_2-k_1)t} \nonumber\]

En el siguiente paso, necesitamos reconocer que el lado izquierdo de la ecuación es la derivada del producto de la variable dependiente multiplicada por el factor integrador:

\[\frac{d}{dt}\left( [B]e^{k_2t}\right)=k_1[A]_0e^{(k_2-k_1)t} \nonumber\]

Luego tomamos '\(dt\)' al lado derecho de la ecuación e integramos ambos lados:

\[\int d \left( [B]e^{k_2t}\right)=\int k_1[A]_0e^{(k_2-k_1)t}dt \nonumber\]

\[[B]e^{k_2t}=\frac{1}{k_2-k_1} k_1[A]_0e^{(k_2-k_1)t}+c \nonumber\]

\[[B]=\frac{1}{k_2-k_1} k_1[A]_0\frac{e^{(k_2-k_1)t}}{e^{k_2t}}+\frac{c}{e^{k_2t}} \nonumber\]

\[[B]=\frac{k_1}{k_2-k_1} [A]_0e^{-k_1t}+ce^{-k_2t} \nonumber\]

Tenemos una constante arbitraria porque se trata de una ecuación diferencial de primer orden. Calculemos\(c\) usando la condición inicial\([B](t=0)=0\):

\[0=\frac{k_1}{k_2-k_1} [A]_0e^{-k_1 0}+ce^{-k_2 0}=\frac{k_1}{k_2-k_1} [A]_0+c \nonumber\]

\[c=-\frac{k_1}{k_2-k_1} [A]_0 \nonumber\]

Y por lo tanto,

\[[B]=\frac{k_1}{k_2-k_1} [A]_0e^{-k_1t}-\frac{k_1}{k_2-k_1} [A]_0e^{-k_2t} \nonumber\]

\[\label{eq:b(t)} [B]=\frac{k_1}{k_2-k_1} [A]_0\left(e^{-k_1t}-e^{-k_2t}\right)\]

Antes de seguir adelante, observe que lo hemos asumido\(k_1\neq k_2\). No fuimos explícitos, pero realizamos la integración con esta suposición. Si\(k_1=k_2\) el término exponencial se convierte en 1, que no es una función de\(t\). En este caso, la integral obviamente será diferente, por lo que nuestra respuesta asume\(k_1\neq k_2\). Esto es una buena noticia, ya que de lo contrario tendríamos que preocuparnos de que el denominador de [eq:b (t)] sea cero. Resolverá el caso\(k_1= k_2\) en Problema 4.4.

Ahora que tenemos [A] y [B], podemos obtener la expresión para [C]. Podríamos usar la ecuación\ ref {consq3}:

\[\frac{d[C]}{dt}=k_2[B]=\frac{k_2k_1}{k_2-k_1} [A]_0\left(e^{-k_1t}-e^{-k_2t}\right) \nonumber\]

Esto no es demasiado difícil porque la ecuación es separable. Sin embargo, es más fácil obtener [C] del balance de masa, Ecuación\ ref {consq4}:

\[[C]=[A]_0-[A]-[B] \nonumber\]

Atrapando las respuestas que obtuvimos para [A] y [B]:

\[[C]=[A]_0-[A]_0e^{-k_1t}-\frac{k_1}{k_2-k_1} [A]_0\left(e^{-k_1t}-e^{-k_2t}\right) \nonumber\]

\[\label{eq:c(t)} [C]=[A]_0\left[1-e^{-k_1t}-\frac{k_1}{k_2-k_1}\left(e^{-k_1t}-e^{-k_2t}\right)\right]\]

Ecuaciones\ ref {eq:a (t)},\ ref {eq:b (t)},\ ref {eq:c (t)} son las soluciones que estábamos buscando. Si tuviéramos los valores de\(k_1\) y\(k_2\) podríamos trazar\([A](t)/[A]_0\),\([B](t)/[A]_0\)\([C](t)/[A]_0\) y ver cómo evolucionan las tres especies con el tiempo. Si lo\([A]_0\) tuviéramos podríamos trazar las concentraciones reales, pero notar que esto no suma demasiado, porque simplemente vuelve a escalar el\(y-\) eje pero no cambia la forma de las curvas.

La figura\(\PageIndex{6}\) muestra los perfiles de concentración para una reacción con\(k_1=0.1 s^{-1}\) y\(k_2=0.5 s^{-1}\). Observe que debido a que B es un intermedio, su concentración primero aumenta, pero luego disminuye a medida que B se convierte en C. El producto C tiene una 'fase de retardo', porque necesitamos esperar hasta que se forme suficiente B antes de que podamos ver aumentar la concentración de C (primer par de segundos en este ejemplo). Como verás después de resolver tus problemas de tarea, el momento en el que el intermedio (B) alcanza su concentración máxima depende de ambos\(k_1\) y\(k_2\).

Figura\(\PageIndex{6}\): Perfiles de concentración para la reacción\(A \overset{k_1}{\rightarrow} B \overset{k_2}{\rightarrow} C\) con\(k_1 = 0.1s^{−1}\) y\(k_2 = 0.5s^{−1}\) (CC BY-NC-SA; Marcia Levitus)

Reacciones reversibles de primer orden

Hasta el momento hemos discutido reacciones irreversibles. Sin embargo, sabemos que muchas reacciones son reversibles, lo que significa que el reactivo y el producto existen en equilibrio:

\[A \xrightleftharpoons[k_2]{k_1} B \nonumber\]

La tasa de cambio de [A],\(\frac{d[A]}{dt}\), es la velocidad a la que aparece A (\(k_2[B]\)) menos la velocidad a la que A desaparece (\(k_1[A]\)):

\[\frac{d[A]}{dt}=k_2[B]-k_1[A] \nonumber\]

No podemos resolver esta ecuación tal como es, porque tiene dos variables dependientes, [A] y [B]. Sin embargo, podemos escribir [B] en términos de [A], o [A] en términos de [B], usando el balance de masas:

\[[A](t)+[B](t)=[A]_0+[B]_0 \nonumber\]

\[\frac{d[A]}{dt}=k_2\left( [A]_0+[B]_0-[A]\right)-k_1[A] \nonumber\]

\[\frac{d[A]}{dt}=k_2\left( [A]_0+[B]_0\right)-\left(k_2+k_1\right)[A] \nonumber\]

Se trata de una ecuación diferencial ordinaria, separable, de primer orden, por lo que puede resolverse mediante integración directa. Resolverás este problema en tu tarea, así que saltemos los pasos y saltemos a la respuesta:

\[\label{eq:aeq} [A]=\frac{k_2\left ( [A]_0+[B]_0 \right )}{k_1+k_2}+\frac{k_1 [A]_0-k_2[B]_0 }{k_1+k_2}e^{-\left (k_1+k_2 \right )t}\]

Esta es una reacción reversible, por lo que si esperamos lo suficiente alcanzará el equilibrio La concentración de [A] en equilibrio, [A]\(_{eq}\), es el límite de la expresión previa cuando\(t\rightarrow \infty\). Porque\(e^{-x}\rightarrow 0\) cuando\(x\rightarrow \infty\):

\[[A]_{eq}=\frac{k_2\left ( [A]_0+[B]_0 \right )}{k_1+k_2} \nonumber\]

y podemos reescribir la Ecuación\ ref {eq:aeq} como

\[\label{eq:aeq2} [A]=[A]_{eq}+\left([A]_0-[A]_{eq}\right)e^{-\left (k_1+k_2 \right )t}\]

Como vas a hacer en tu tarea, podemos calcular\([B](t)\) a partir del balance de masa como\([B](t)=[A]_0+[B]_0-[A](t)\).

La ecuación\ ref {eq:aeq2} no es muy diferente de la ecuación\ ref {eq:mdecay}. En el caso de una reacción irreversible, (Ecuación\ ref {eq:mdecay}), [A] decae de un valor inicial [A]\(_0\) a un valor final\([A]_{t \rightarrow \infty}=0\) con un tiempo de relajación\(\tau=1/k\). Para la reacción reversible,\([A]-[A]_{eq}\) decae de un valor inicial\([A]_0-[A]_{eq}\) a un valor final\([A]_{t \rightarrow \infty}-[A]_{eq}=0\) con un tiempo de relajación\(\tau=(k_1+k_2)^{-1}\). ¡Esta última declaración no es trivial! Dice que la velocidad a la que una reacción se acerca al equilibrio depende de la suma de las constantes de velocidad hacia adelante y hacia atrás.

Figura\(\PageIndex{7}\): La cinética de una reacción con\([\text{A}]_0 = 0.1M\),\(k_1 = 0.1s^{−1}\) y\(k_2 = 0.2s^{−1}\) aproximándose al equilibrio. Tenga en cuenta que el tiempo de relajación es\(3s = (k_1 + k_2)^{−1}\) (CC BY-NC-SA; Marcia Levitus)

En tu tarea se te pedirá que pruebes que la relación de las concentraciones en equilibrio,\([B]_{eq}/[A]_{eq}\) es igual a la relación de las constantes de tasa hacia adelante y hacia atrás. Además, de tus cursos introductorios de química debes saber que la constante de equilibrio de una reacción (\(K_{eq}\)) es la relación de las concentraciones de equilibrio de producto de reactivo. Por lo tanto:

\[\label{eq:eql} \frac{[B]_{eq}}{[A]_{eq}}=K_{eq}=\frac{k_1}{k_2}\]

Esto significa que podemos calcular la relación de\(k_1\) y\(k_2\) a partir de las concentraciones de A y B que observamos una vez que se ha alcanzado el equilibrio (es decir, una vez\(\frac{d[A]}{dt}=\frac{d[B]}{dt}=0\)). Al mismo tiempo, podemos obtener la suma de\(k_1\) y\(k_2\) a partir del tiempo de relajación del proceso. Si tenemos la suma y la relación, podemos calcular ambas\(k_1\) y\(k_2\). Todo esto tiene sentido, pero requiere que podamos observar la reacción desde un estado inicial fuera del equilibrio. Si el sistema ya está en equilibrio,\([A]_0=[A]_{eq}\), y\(d[A]/dt=0\) en todo momento. Una parcela de [A]\((t)\) se verá plana, y no podremos extraer el tiempo de relajación de la reacción. Si, sin embargo, tenemos una forma experimental de cambiar el equilibrio así\([A]_0\neq[A]_{eq}\), podemos medir el tiempo de relajación observando cómo la reacción vuelve a su posición de equilibrio.

Tema avanzado: ¿Cómo podemos cambiar el equilibrio? Una forma es producir un cambio muy rápido en la temperatura del sistema. La constante de equilibrio de una reacción suele depender de la temperatura, por lo que si un sistema se equilibre a una temperatura dada (digamos\(25^{\circ}C\)), y de repente aumentamos la temperatura (por ejemplo, a\(26^{\circ}C\)), la reacción repentinamente estará lejos de su condición de equilibrio a la nueva temperatura. Podemos ver cómo el sistema se relaja a las concentraciones de equilibrio en\(26^{\circ}C\), y medir el tiempo de relajación. Esto nos permitirá calcular las constantes de tasa en\(26^{\circ}C\).

\[\frac{[B]_{eq}}{[A]_{eq}}=K_{eq}=\frac{k_1}{k_2} \nonumber\]

Ejemplo\(\PageIndex{1}\)

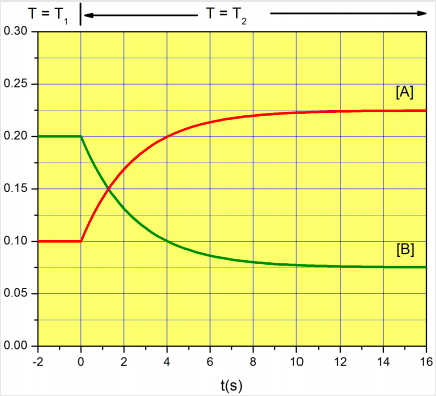
Tema avanzado La siguiente figura ilustra el procedimiento experimental conocido como “salto en T”, en el que se utiliza un cambio repentino de temperatura para desplazar la posición de una reacción reversible fuera de equilibrio. El experimento comienza a una temperatura\(T_1\), y la temperatura se incrementa\(T_2\) instantáneamente en el momento\(t=0\). Debido a que la constante de equilibrio at\(T_2\) es diferente de la constante de equilibrio at\(T_1\), el sistema necesita relajarse al nuevo estado de equilibrio. De la siguiente gráfica estime a lo mejor de sus habilidades\(K_{eq} (T_1)\),\(K_{eq} (T_2)\), y las constantes de tasa\(k_1\), y\(k_2\) en\(T_2\).

\[A \xrightleftharpoons[k_2]{k_1} B \nonumber\]

Solución

En\(T_1\),\([A]_{eq}=0.1 M\) y\([B]_{eq}=0.2 M\). La constante de equilibrio es\([B]_{eq}/[A]_{eq}=2\).

En\(T_2\),\([A]_{eq}=0.225 M\) y\([B]_{eq}=0.075 M\). La constante de equilibrio es\([B]_{eq}/[A]_{eq}=1/3\).

Porque\(K_{eq}=\frac{k_1}{k_2}\), a\(T=T_2\),\(\frac{k_1}{k_2}=1/3\). Para calcular el tiempo de relajación veamos la expresión para\([A](t)\) (Ecuación\ ref {eq:aeq2}).

\[[A]=[A]_{eq}+\left([A]_0-[A]_{eq}\right)e^{-\left (k_1+k_2 \right )t} \nonumber\]

Cuando el tiempo es igual al tiempo de relajación (\(\tau=(k_1+k_2)^{-1}\)),

\[[A](t=\tau)=[A]_{eq}+\left([A]_0-[A]_{eq}\right)e^{-1} \nonumber\]

\[[A](t=\tau)\approx 0.225M+\left(0.1M-0.225M\right)\times 0.37\approx 0.18 \nonumber\]¹

De la gráfica,\([A]=0.18\) a\(t = 2.5s\), y por lo tanto el tiempo de relajación es\(\tau=(k_1+k_2)^{-1}= 2.5s\).

Tenemos\((k_1+k_2)^{-1}= 2.5s = 5/2 s\) y\(\frac{k_1}{k_2}=1/3\):

\[(k_1+k_2)=2/5= (k_1+3k_1)=4k_1\rightarrow k_1=1/10 = 0.1 s^{-1}, k_2=0.3 s^{-1} \nonumber\]