7.2: Serie de Fourier
- Page ID
- 70065
Una serie de Fourier es una combinación lineal de funciones sinusoidales y cosenales, y está diseñada para representar funciones periódicas:
\[\label{eq:fourier} f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}a_n \cos\left ( \dfrac{n\pi x}{L} \right )+\sum_{n=1}^{\infty}b_n \sin\left ( \dfrac{n\pi x}{L} \right )\]
Los coeficientes\(a_0, a_1,a_2...a_n\) y\(b_1, b_2....b_n\) son constantes.
Es importante notar que el periodo de las funciones seno y coseno en la Ecuación\ ref {eq:fourier} es\(P=2L/n\) (ver Sección 1.4). Esto quiere decir que vamos a estar mezclando senos y cosenos de periodos\(2L\)\(2L/2\),\(2L/3\),\(2L/4\),, etc. Como veremos, esta combinación lineal dará como resultado una función periódica de periodo\(P = 2L\).
Además, solo necesitamos los términos impares (las funciones sinusoidales) para representar una función periódica impar, por lo que en este caso todos los\(a_n\) coeficientes (incluyendo\(a_0\)) serán cero. Solo necesitamos términos pares (las funciones coseno) para representar una función par, así que en este caso todos los\(b_n\) coeficientes serán cero. ¿Por qué no tenemos\(b_0\) término? Esto es porque\(\sin{(0)}=0\). En el caso de los términos coseno, el\(n=0\) término se separa de la suma, pero no se desvanece porque\(\cos{(0)}\neq0\).
Esto significa que una función periódica impar con punto\(P=2L\) será en general:
\[f(x)= b_1 \sin{\left(\dfrac{\pi x}{L}\right)}+b_2 \sin{\left(\dfrac{2\pi x}{L}\right)}+b_3 \sin{\left(\dfrac{3\pi x}{L}\right)}... \nonumber\]
Digamos que queremos construir una función periódica impar de punto\(P=2\pi\). Porque el periodo es\(2L\), esto quiere decir que\(L=\pi\):
\[f(x)= b_1 \sin{\left(x\right)}+b_2 \sin{\left(2x\right)}+b_3 \sin{\left(3x\right)}... \nonumber\]
De hecho ya vimos un ejemplo como este en la Figura\(7.1.2\) (derecha). Esta función periódica, que se construye utilizando\(b_n=1/n\), tiene un periodo de\(2\pi\) como acabamos de predecir. Veamos otros ejemplos con diferentes coeficientes:
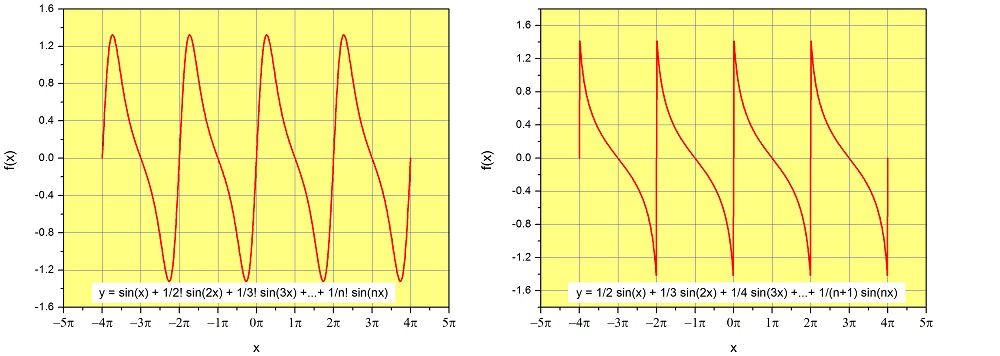
Observe que estamos mezclando las funciones\(\sin{\left(x\right)}, \sin{\left(2x\right)},\sin{\left(3x\right)}...\) usando diferentes coeficientes, y siempre creamos una función periódica con punto\(P=2\pi\).
Volviendo a la Ecuación\ ref {eq:fourier}, sabemos que diferentes coeficientes crearán diferentes funciones periódicas, pero todos tendrán un periodo\(2L\). La pregunta obvia ahora es cómo calcular los coeficientes que van a crear la función que queremos. Digamos que la función periódica se construye mediante una extensión periódica de la función\(f(x)\), que se define en el intervalo\([-L,L]\). Un ejemplo sería la función de Figura\(7.1.5\), que se define en el intervalo\([-\pi,\pi]\). Si creamos la extensión periódica de esta función, crearemos una función periódica con punto\(2\pi\). Análogamente, al crear una extensión periódica de una función definida en el intervalo\([-L,L]\) crearemos una función periódica con punto\(2L\). Los coeficientes de la Ecuación\ ref {eq:fourier} se calculan de la siguiente manera:
\[\label{ao} a_0=\dfrac{1}{L}\int_{-L}^{L}f(x)dx\]
\[\label{an} a_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\cos{\left(\dfrac{n\pi x}{L} \right)}dx\]
\[\label{bn} b_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\sin{\left(\dfrac{n\pi x}{L} \right)}dx\]
Observe que la Ecuación\ ref {ao} es un caso especial de Ecuación\ ref {an}, y que no tenemos un coeficiente\(b_0\) porque\(\sin{(0)}=0\). Debido a que la ecuación\ ref {eq:fourier} representa una función periódica con punto\(2L\), la integración se realiza sobre un período centrado en cero (es decir,\(L\) es la mitad del período).
Formulación alternativa
La ecuación\ ref {eq:fourier} a menudo se escribe como:
\[\label{eq:fourier_alt} f(x)=a_0+\sum_{n=1}^{\infty}a_n \cos\left ( \dfrac{n\pi x}{L} \right )+\sum_{n=1}^{\infty}b_n \sin\left ( \dfrac{n\pi x}{L} \right )\]
Si elegimos hacer esto, por supuesto necesitamos redefinir el coeficiente\(a_0\) como:
\[a_0=\dfrac{1}{2L}\int_{-L}^{L}f(x)dx. \nonumber\]
Ambas versiones dan por supuesto la misma serie, y si eliges una u otra es cuestión de gustos. Puede que veas las dos versiones en diferentes libros de texto, ¡así que no te confundas!.
Ejemplo\(\PageIndex{1}\)
Obtener la serie de Fourier de la función periódica representada en la figura.

Solución
\(y(x)\)es una función periódica con punto\(P=2\). Se puede construir mediante la extensión periódica de la función\(f(x)=2x\), definida en el intervalo\([-1,1]\). Observe que este intervalo tiene un ancho igual al periodo, y está centrado en cero.
Porque\(y(x)\) es extraño, no vamos a molestarnos en calcular los coeficientes\(a_n\). Podríamos, pero obtendríamos cero para todos ellos. La ecuación\ ref {eq:fourier}, por lo tanto, se reduce a:
\[y(x)=\sum\limits_{n=1}^{\infty}b_n sin\left ( \dfrac{n\pi x}{L} \right ) \nonumber\]
A partir de la ecuación\ ref {bn}, los coeficientes\(b_n\) se calculan como:
\[b_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\sin{\left(\dfrac{n\pi x}{L} \right)}dx \nonumber\]
y en este caso, porque\(L=1\) (la mitad del periodo),
\[b_n=\int_{-1}^{1}(2x)\sin{\left(n\pi x \right)}dx=2\int_{-1}^{1}x\sin{\left(n\pi x \right)}dx \nonumber\]
La primitiva de\(\int x\sin{\left(a x \right)}dx\) es\(\dfrac{\sin{(ax)}}{a^2}-\dfrac{x \cos{(ax)}}{a}\) (ver hoja de fórmulas), entonces
\[b_n=2\int_{-1}^{1}x\sin{\left(n\pi x \right)}dx=2\left[\dfrac{\sin{(n \pi)}}{(n\pi)^2}-\dfrac{\cos{(n\pi)}}{n \pi}-\left(\dfrac{\sin{(n \pi (-1))}}{(n\pi)^2}-\dfrac{(-1) \cos{(n\pi (-1))}}{n \pi}\right)\right] \nonumber\]
Usando el hecho de que\(\sin{(n\pi)}\) es cero y\(\cos{x}\) es una función par:
\[b_n=-4\dfrac{ \cos{(n\pi)}}{n \pi} \nonumber\]
Escribamos algunos términos en una tabla:
| \(n\) | \(\cos{(n\pi)}\) | \(b_n\) |
|---|---|---|
| \ (n\)” style="text-align:center; ">1 | \ (\ cos {(n\ pi)}\)” style="text-align:center; ">-1 | \ (b_n\)” style="text-align:center; ">\(\dfrac{4}{\pi}\) |
| \ (n\)” style="text-align:center; ">2 | \ (\ cos {(n\ pi)}\)” style="text-align:center; ">1 | \ (b_n\)” style="text-align:center; ">\(-\dfrac{4}{2\pi}\) |
| \ (n\)” style="text-align:center; ">3 | \ (\ cos {(n\ pi)}\)” style="text-align:center; ">-1 | \ (b_n\)” style="text-align:center; ">\(\dfrac{4}{3\pi}\) |
| \ (n\)” style="text-align:center; ">4 | \ (\ cos {(n\ pi)}\)” style="text-align:center; ">1 | \ (b_n\)” style="text-align:center; ">\(-\dfrac{4}{4\pi}\) |
| \ (n\)” style="text-align:center; ">5 | \ (\ cos {(n\ pi)}\)” style="text-align:center; ">-1 | \ (b_n\)” style="text-align:center; ">\(\dfrac{4}{5\pi}\) |
Una expresión general para\(b_n\) es:
\[b_n=4 \dfrac{(-1)^{n+1}}{n\pi} \nonumber\]
La serie
\[y(x)=\sum_{n=1}^{\infty}b_n sin\left ( \dfrac{n\pi x}{L} \right ) \nonumber\]
es entonces:
\[\label{eq:sawtooth} \displaystyle{\color{Maroon}y(x)=\dfrac{4}{\pi}\sum_{n=1}^{\infty}\dfrac{(-1)^{n+1}}{n} sin\left (n\pi x \right )}\]
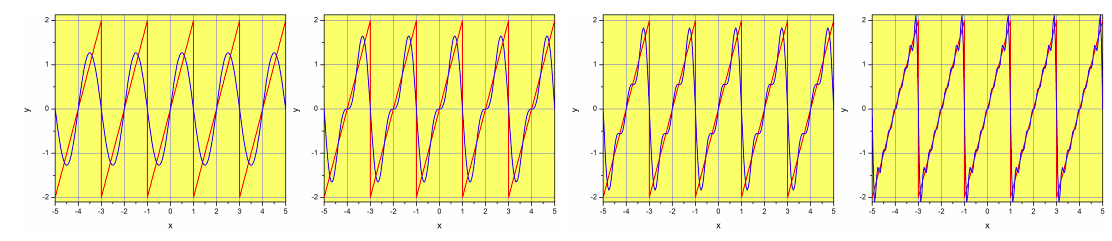
Como en el caso de una serie de Taylor, la Ecuación\ ref {eq:diente de sierra} es exacta si incluimos los términos infinitos de la serie. Si truncamos la serie usando un número finito de términos, crearemos una aproximación. La figura\(\PageIndex{1}\) muestra un ejemplo con 1, 2, 3 y 8 términos.
Ejemplo\(\PageIndex{2}\)
Obtener la serie de Fourier de la onda cuadrada formada por la extensión periódica de la función:
\[f(x)=\left\{\begin{matrix}0 & -\pi\leq x\leq 0 \\ 1 &0<x\leq \pi \end{matrix}\right. \nonumber\]
Solución
La extensión periódica de la función\(f(x)\) produce una función periódica con punto\(2\pi\):
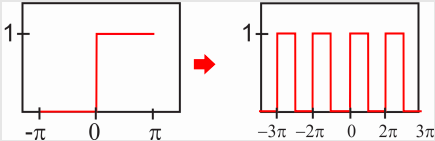
Estrictamente hablando, la función periódica resultante no es ni par ni impar, por lo que necesitaríamos calcular todos los coeficientes. Sin embargo, puede notar que la función sería impar si restáramos 1/2 de todos los puntos. En otras palabras, la función periódica que estamos buscando será una constante (\(a_0\)) más una función periódica impar (serie sinusoidal). Vamos a calcular la constante, pero a partir de esta discusión debería ser obvio que vamos a conseguir\(a_0/2=1/2\). También calcularemos el resto de los\(a_n\) coeficientes, pero ahora sabemos que todos serán cero.
El primer coeficiente,\(a_0\) es (Ecuación\ ref {ao}):
\[a_0=\dfrac{1}{L}\int_{-L}^{L}f(x)dx \nonumber\]
Aquí,\(L=\pi\) (la mitad del periodo), entonces:
\[a_0=\dfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx=\dfrac{1}{\pi}\int_{0}^{\pi}1dx=1 \nonumber\]
donde hemos utilizado el hecho de que\(f(x)=0\) en el intervalo\(-\pi<x<0\). Los coeficientes\(a_n\) son (Ecuación\ ref {an})
\[a_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\cos{\left(\dfrac{n\pi x}{L} \right)}dx=\dfrac{1}{\pi}\int_{0}^{\pi}\cos{\left(n x \right)}dx=\dfrac{1}{\pi}\left.\begin{matrix}\left ( \dfrac{sin(n\pi))}{n} \right )\end{matrix}\right|_0^\pi=0 \nonumber\]
Los coeficientes\(b_n\) son (Ecuación\ ref {bn})
\[b_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\sin{\left(\dfrac{n\pi x}{L} \right)}dx=\dfrac{1}{\pi}\int_{0}^{\pi}\sin{\left(n x \right)}dx=\dfrac{1}{\pi}\left.\begin{matrix}\left ( -\dfrac{cos(n\pi))}{n} \right )\end{matrix}\right|_0^\pi=-\dfrac{1}{\pi n}(\cos{(n\pi)}-cos{(0)})=\dfrac{1-\cos{(n\pi)}}{n\pi} \nonumber\]
Veamos algunos términos en una tabla:
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| \ (n\)” style="text-align:center; ">\(\cos{(n\pi)}\) | -1 | 1 | -1 | 1 | -1 | 1 |
| \ (n\)” style="text-align:center; ">\(b_n\) | \(\dfrac{2}{\pi}\) | \(0\) | \(\dfrac{2}{3\pi}\) | \(0\) | \(\dfrac{2}{5\pi}\) | 0 |
La serie es (Ecuación\ ref {eq:fourier})
\[f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}a_n cos\left( \dfrac{n\pi x}{L} \right)+\sum_{n=1}^{\infty}b_n sin\left( \dfrac{n\pi x}{L} \right) \nonumber\]
y con los coeficientes que tenemos podemos escribir:
\[f(x)=\dfrac{1}{2}+\dfrac{2}{\pi}\sin{(x)}+\dfrac{2}{3\pi}\sin{(3x)}+\dfrac{2}{5\pi}\sin{(5x)}... \nonumber\]
o más elegantemente:
\[\displaystyle{\color{Maroon}\dfrac{1}{2}+\dfrac{2}{\pi} \sum_{n=0}^{\infty}\dfrac{1}{2n+1}\sin{[(2n+1)x]}} \nonumber\]
Observe que, como era de esperar, tenemos una serie sinusoidal (que representa una función periódica impar) más una constante (que 'empuja' la función hacia arriba).
¿Necesitas ayuda? Los enlaces a continuación contienen ejemplos resueltos.
Enlaces externos:
- Ejemplo de la serie de Fourier I: http://www.youtube.com/watch?v=jzzpxqVohhI
- Ejemplo II de la serie de Fourier: http://www.youtube.com/watch?v=edwG9x5v3Xo

