8.4: Integrales dobles y triples

Podemos extender la idea de una integral definida a más dimensiones. Si\(f(x,y)\) es continuo sobre el rectángulo\(R=[a,b]\times[c,d]\) entonces,

\[\label{c2v:eq:doubleint} \underset{R}{\iint}f(x,y)dA=\int_{a}^{b}\int_{c}^{d}f{(x,y)\, dy\, dx}=\int_{c}^{d}\int_{a}^{b}f{(x,y)\, dx\, dy}\]

Si\(f(x,y)\geq0\), entonces la doble integral representa el volumen\(V\) del sólido que se encuentra por encima del rectángulo\(R\) y por debajo de la superficie\(z=f(x,y)\) (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Interpretación geométrica de una doble integral (CC BY-NC-SA; Marcia Levitus)

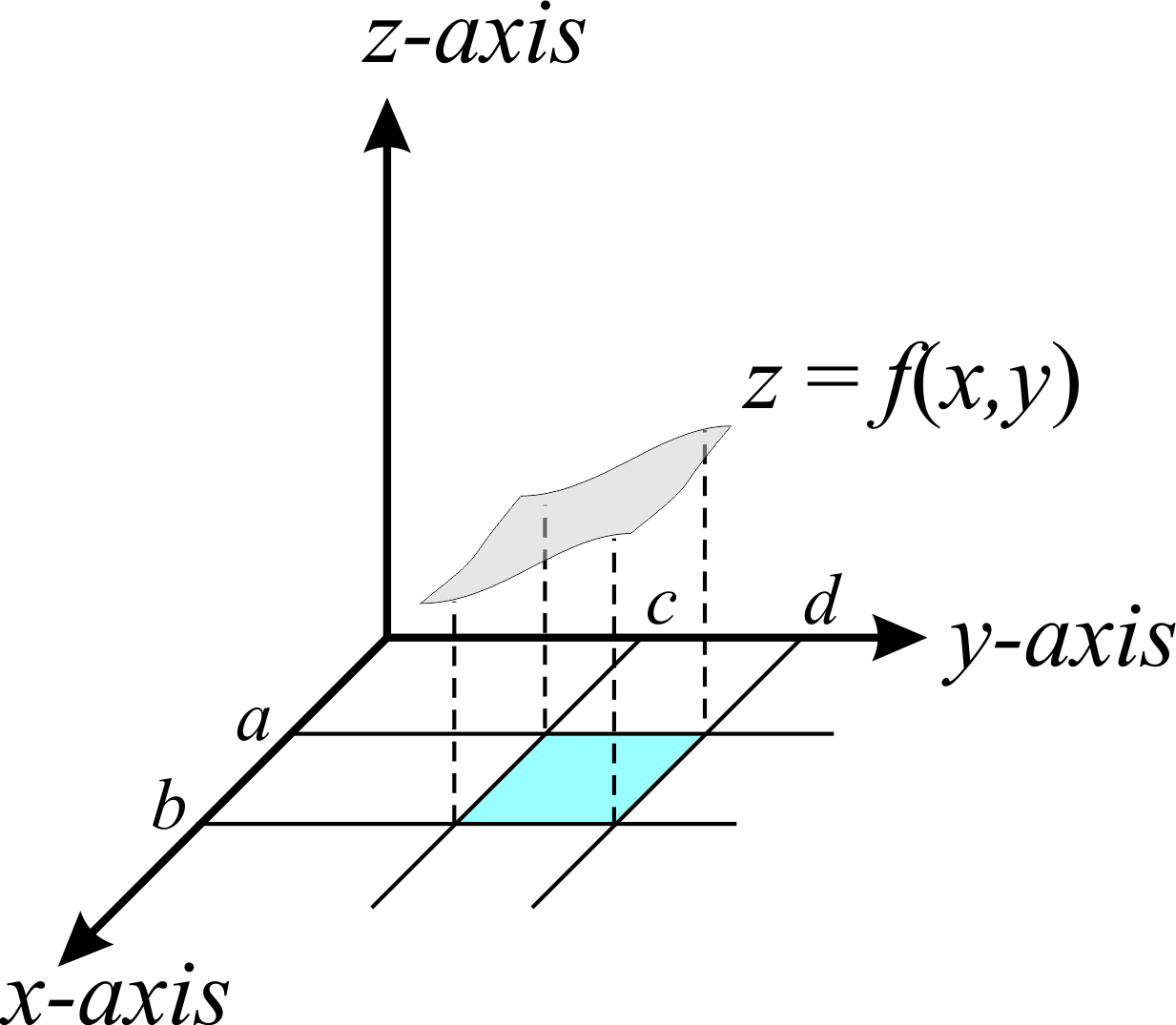
Podemos calcular la doble integral de la ecuación\ ref {c2v:eq:doubleint} como:

\[\underset{R}{\iint}f(x,y)dA=\int_{a}^{b}\left[ \int_{c}^{d}f{(x,y)\, dy} \right]dx \nonumber\]

lo que significa que primero vamos a calcular

\[\int_{c}^{d}f{(x,y)\, dy} \nonumber\]

\(x\)manteniéndose constante e integrándose con respecto a\(y\). El resultado será una función que contenga únicamente\(x\), la cual integraremos entre\(a\) y\(b\) con respecto a\(x\).

Por ejemplo, vamos a resolver\(\int_{0}^{3}\int_{1}^{2}{x^2 y\; dy\; dx}\). Empezaremos resolviendo\(\int_{1}^{2}{x^2 y\; dy}\) mantener\(x\) constante:

\[\int_{1}^{2}{x^2 y\; dy}=x^2\int_{1}^{2}{y\; dy}=\dfrac{3}{2}x^2 \nonumber\]

Ahora integramos esta función de 0 a 3 con respecto a\(x\):

\[\int_{0}^{3}\int_{1}^{2}{x^2 y\; dy\; dx}=\int_{0}^{3}{\dfrac{3}{2}x^2 \; dx}=\dfrac{27}{2} \nonumber\]

Por supuesto, puede integrar de 0 a 3 primero con respecto a\(x\) mantener\(y\) constante, y luego integrar el resultado con respecto a\(y\) de 1 a 2. Pruébalo de esta manera y verifica que obtengas el mismo resultado.

Las integrales triples funcionan de la misma manera. Si\(f(x,y,z)\) es continuo en la caja rectangular\(B=[a,b]\times[c,d]\times[r,s]\), entonces

\[\label{c2v:eq:tripleint} \underset{B}{\iiint}f(x,y,z)dV=\int_{r}^{s}\int_{c}^{d}\int_{a}^{b}f{(x,y)\, dx\, dy\, dz}\]

Esta integral iterada significa que integramos primero con respecto a\(x\) (mantener\(y\) y\(z\) fijar), luego integramos con respecto a\(y\) (mantenernos\(z\) fijos), y finalmente integramos con respecto a\(z\). Hay otros cinco órdenes posibles en los que podemos integrarnos, todos los cuales dan el mismo valor.

¿Necesitas un repaso en integrales dobles y triples? Consulta los videos a continuación antes de pasar a los ejemplos de química física.

• Ejemplo 1: http://www.youtube.com/watch?v=RqD89-afGS0
• Ejemplo 2: http://www.youtube.com/watch?v=CPR0ZD0IYVE (consulta el ejemplo que comienza alrededor de las 3:45 min. y termina a las 5:07 min)

Las triples integrales se utilizan muy a menudo en la química física para normalizar las funciones de densidad de probabilidad. Por ejemplo, en la mecánica cuántica, el cuadrado absoluto de la función de onda\(\left | \psi (x,y,z) \right |^2\),, se interpreta como una densidad de probabilidad, la probabilidad de que la partícula esté dentro del volumen\(dx.dy.dz\). Dado que la probabilidad de encontrar la partícula en algún lugar del espacio es 1, requerimos que:

\[\label{c2v:eq:calculus2v_normalization} \int_{-\infty }^{\infty }\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz=1\]

Ya mencionamos las funciones de onda en la Sección 2.3, donde demostramos que

\[\left | \psi (x,y,z) \right |^2=\psi^*(x,y,z) \psi(x,y,z) \nonumber\]

La condición de normalización, por lo tanto, también puede escribirse como

\[\label{c2v:eq:calculus2v_normalization2} \int_{-\infty }^{\infty }\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }{ \psi^*\psi }\; dx \;dy \;dz=1\]

Ejemplo\(\PageIndex{1}\)

En mecánica cuántica, el estado de energía más bajo de una partícula confinada en una caja tridimensional está representado por

\[\psi (x,y,z)=A\sin{\dfrac{\pi x}{a}}\sin{\dfrac{\pi y}{b}}\sin{\dfrac{\pi z}{c}}\; if\; \left\{ \begin{matrix} 0< x< a\\ 0< y< b\\ 0< z< c\\ \end{matrix} \right. \]

y

\(\psi (x,y,z)=0\)de lo contrario (fuera de la caja).

Aquí,\(A\) es una constante de normalización, y\(a\),\(b\) y\(c\) son las longitudes de los lados de la caja. Dado que la probabilidad de encontrar la partícula en algún lugar del espacio es 1, requerimos que

\[\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz=1 \nonumber\]

Encuentra la constante de normalización\(A\) en términos de\(a,b,c\) y otras constantes.

Solución

Porque\(\psi(x,y,z)=0\) fuera de la caja,

\[\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz=\int_{0 }^{c }\int_{0 }^{b }\int_{0 }^{a }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz = \left | \psi (x,y,z) \right |^2=\psi^* (x,y,z) \psi(x,y,z) \nonumber\]

No obstante, debido a que en este caso la función es real,

\[\left | \psi (x,y,z) \right |^2=\left ( \psi (x,y,z) \right )^2\]

\[\int_{0 }^{c }\int_{0 }^{b }\int_{0 }^{a }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz=\int_{0 }^{c }\int_{0 }^{b }\int_{0 }^{a }{A^2 \sin^2\left( \dfrac{\pi x}{a}\right)\sin^2\left( \dfrac{\pi y}{b}\right)\sin^2\left( \dfrac{\pi z}{c}\right)}\; dx \;dy \;dz=1 \nonumber\]

\[\int_{0 }^{c }\int_{0 }^{b }\int_{0 }^{a }{A^2 \sin^2\left( \dfrac{\pi x}{a}\right)\sin^2\left( \dfrac{\pi y}{b}\right)\sin^2\left( \dfrac{\pi z}{c}\right)}\; dx \;dy \;dz= A^2\int_{0 }^{a }{\sin^2\left( \dfrac{\pi x}{a}\right)}dx\int_{0 }^{b }{\sin^2\left( \dfrac{\pi y}{b}\right)}dy\int_{0 }^{c }{\sin^2\left( \dfrac{\pi z}{c}\right)}dz \nonumber\]

Usando la hoja de fórmulas, obtenemos

\[\int_{0 }^{a }{\sin^2\left( \dfrac{\pi x}{a}\right)}dx=a/2 \nonumber\]

Y por lo tanto,

\[A^2\int_{0 }^{a }{\sin^2\left( \dfrac{\pi x}{a}\right)}dx\int_{0 }^{b }{\sin^2\left( \dfrac{\pi y}{b}\right)}dy\int_{0 }^{c }{\sin^2\left( \dfrac{\pi z}{c}\right)}dz=A^2 \dfrac{a}{2} \dfrac{b}{2}\dfrac{c}{2}=\dfrac{A^2abc}{8}=1 \nonumber\]

Resolviendo para\(A\):

\[\displaystyle{\color{Maroon}A=\left( \dfrac{8}{abc}\right)^{1/2}}\]