8.3: La regla de la cadena

Todos sabemos que la posición de un punto en el espacio se puede especificar con dos coordenadas,\(x\) y\(y\), llamadas las coordenadas cartesianas. También sabemos que podemos elegir en su lugar especificar la posición del punto usando la distancia desde el origen (\(r\)) y el ángulo que el vector hace con el\(x\) eje (\(\theta\)). Estos últimos son lo que llamamos coordenadas polares de avión, que cubriremos con mucho más detalle en el Capítulo 10.

Figura\(\PageIndex{1}\): Coordenadas cartesianas y polares. (CC BY-NC-SA; Marcia Levitus)

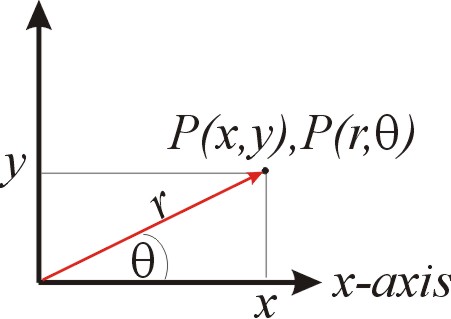
Los dos sistemas de coordenadas están relacionados por:

\[\label{c2v:eq:calculus2v_cartesian} x=r\cos{\theta}; \; \;y=r\sin{\theta}\]

\[\label{c2v:eq:calculus2v_polar} r=\sqrt{x^2+y^2}; \; \; \theta=tan^{-1}(y/x)\]

Supongamos que se nos da una función en coordenadas polares, por ejemplo\(f(r,\theta)=e^{-3r}\cos{\theta}\), y se nos pide encontrar las derivadas parciales en coordenadas cartesianas,\((\partial f/\partial x)_y\) y\((\partial f/\partial y)_x\). Por supuesto, podemos reescribir la función en términos de\(x\) y\(y\) y encontrar las derivadas que necesitamos, pero ¿no sería maravilloso si tuviéramos una fórmula universal que convierta las derivadas en coordenadas polares (\((\partial f/\partial r)_\theta\)y\((\partial f/\partial \theta)_r\)) a las derivadas en coordenadas cartesianas? Esto nos permitiría tomar las derivadas en el sistema en el que se expresa la ecuación (lo cual es fácil), para luego traducir las derivadas al otro sistema sin pensar demasiado. La regla de la cadena nos permitirá crear estas relaciones 'universales' entre las derivadas de diferentes sistemas de coordenadas.

Antes de usar la regla de la cadena, obtengamos\((\partial f/\partial x)_y\) y\((\partial f/\partial y)_x\) reescribiremos la función en términos de\(x\) y\(y\). Quiero mostrarte cuánto trabajo implicaría esto, para que puedas apreciar lo útil que es usar la regla de la cadena. Usando Ecuaciones\ ref {c2v:eq:calculus2v_cartesian} y\ ref {c2v:eq:calculus2v_polar}, podemos reescribir\(f(r,\theta)=e^{-3r}\cos{\theta}\) como

\[f(x,y)=\dfrac{e^{-3(x^2+y^2)^{1/2}}x}{(x^2+y^2)^{1/2}} \nonumber\]

Podemos obtener fácilmente\((\partial f/\partial x)_y\) y\((\partial f/\partial y)_x\), pero sin duda es bastante trabajo. Y si te dijera que\((\partial f/\partial x)_y\) es simplemente

\[\label{c2v:eq:calculus2v_chain1} \left(\dfrac{\partial f}{\partial x}\right)_y=\cos{\theta}\left(\dfrac{\partial f}{\partial r}\right)_\theta-\dfrac{\sin{\theta}}{r}\left(\dfrac{\partial f}{\partial \theta}\right)_r\]

independientemente de la función\(f\)? Derivaremos este resultado en breve, pero por ahora permítanme mencionar que el procedimiento implica usar la regla de la cadena. Probablemente estés suspirando de alivio, porque los derivados\((\partial f/\partial r)_\theta\) y\((\partial f/\partial \theta)_r\) son mucho más fáciles de obtener:

\[\left(\dfrac{\partial f}{\partial r}\right)_\theta=-3e^{-3r}\cos{\theta} \nonumber\]

\[\left(\dfrac{\partial f}{\partial \theta}\right)_r=-e^{-3r}\sin{\theta} \nonumber\]

y usando la ecuación\ ref {c2v:eq:calculus2v_chain1}, podemos obtener la derivada que estamos buscando:

\[\left(\dfrac{\partial f}{\partial x}\right)_y=-\cos{\theta}\times3e^{-3r}\cos{\theta}+\dfrac{\sin{\theta}}{r}e^{-3r}\sin{\theta} \nonumber\]

\[\left(\dfrac{\partial f}{\partial x}\right)_y=-\cos^2{\theta}\times3e^{-3r}+\dfrac{\sin^2{\theta}}{r}e^{-3r}=e^{-3r}\left(\dfrac{\sin^2{\theta}}{r}-3\cos^2{\theta}\right) \nonumber\]

\[\left(\dfrac{\partial f}{\partial x}\right)_y=e^{-3{(x^2+y^2)^{1/2}}}\left(\dfrac{y^2}{(x^2+y^2)^{3/2}}-3\dfrac{x^2}{(x^2+y^2)}\right) \nonumber\]

Ojalá esto no fuera demasiado doloroso, o al menos, menos tedioso que hubiera sido de no haber usado la regla de la cadena. ¿Y qué pasa\((\partial f/\partial y)_x\)? Podemos crear una expresión similar a la Ecuación\ ref {c2v:eq:calculus2v_chain1} y usarla para relacionarse\((\partial f/\partial y)_x\) con\((\partial f/\partial r)_\theta\) y\((\partial f/\partial \theta)_r\).

En este punto puede estar pensando que todo esto funcionó bien porque la función que teníamos era más fácil de derivar en coordenadas polares que en coordenadas cartesianas. Cierto, pero esto es todo el punto. Muchos sistemas físicos se describen en coordenadas polares de forma más natural que en coordenadas cartesianas (especialmente en tres dimensiones). Esto tiene que ver con la simetría del sistema. Para un átomo, por ejemplo, es mucho más natural usar coordenadas esféricas que coordenadas cartesianas. Podríamos usar cartesianas, pero las expresiones serían mucho más complejas y difíciles de trabajar con ellas. Si tenemos ecuaciones que se expresan más fácilmente en coordenadas polares, obtener las derivadas en coordenadas polares siempre será más fácil. Pero, ¿por qué querríamos entonces las derivadas en coordenadas cartesianas? Un gran ejemplo es la ecuación de Schrödinger, que está en el centro de la mecánica cuántica. Hablaremos más de esto cuando discutamos operadores, pero por ahora, la ecuación de Schrödinger es una ecuación diferencial parcial (a menos que la partícula se mueva en una dimensión) que puede escribirse como:

\[E\psi(\vec{r})=-\dfrac{\hbar}{2m}\nabla^2\psi(\vec{r})+V(\vec{r})\psi{(\vec{r})} \nonumber\]

Debido a la simetría del sistema, para átomos y moléculas es más sencillo expresar la posición de la partícula (\(\vec{r}\)) en coordenadas esféricas. Sin embargo, el operador\(\nabla^2\) (conocido como el Laplaciano) se define en coordenadas cartesianas como:

\[\nabla^2f(x,y,z)=\left(\dfrac{\partial^2 f}{\partial x^2}\right)_{y,z}+\left(\dfrac{\partial^2 f}{\partial y^2}\right)_{x,z}+\left(\dfrac{\partial^2 f}{\partial z^2}\right)_{x,y} \nonumber\]

Es decir, el laplaciano te instruye a tomar las segundas derivadas de la función con respecto a\(x\), respecto\(y\) y con respecto a\(z\), y sumar las tres juntas. Podríamos expresar las funciones\(V(\vec{r})\) y\(\psi{(\vec{r})}\) en coordenadas cartesianas, pero nuevamente, esto conduciría a una ecuación diferencial terriblemente compleja. En cambio, podemos expresar el Laplaciano en coordenadas esféricas, y este es de hecho el mejor enfoque. Para ello, necesitaríamos relacionar las derivadas en coordenadas esféricas con las derivadas en coordenadas cartesianas, y esto se hace usando la regla de cadena.

Ojalá todo esto te convenciera de los usos de la regla de la cadena en las ciencias físicas, así que ahora solo necesitamos ver cómo usarla para nuestros fines. En dos dimensiones, la regla de la cadena establece que si tenemos una función en un sistema de coordenadas\(u(x,y)\), y estas coordenadas son funciones de otras dos variables (por ejemplo\(x=x(\theta,r)\) y\(y=y(\theta,r)\)) entonces:

\[\left ( \dfrac{\partial u}{\partial r} \right )_\theta=\left ( \dfrac{\partial u}{\partial x} \right )_y\left ( \dfrac{\partial x}{\partial r} \right )_\theta+\left ( \dfrac{\partial u}{\partial y} \right )_x\left ( \dfrac{\partial y}{\partial r} \right )_\theta\]

\[\left ( \dfrac{\partial u}{\partial \theta} \right )_r=\left ( \dfrac{\partial u}{\partial x} \right )_y\left ( \dfrac{\partial x}{\partial \theta} \right )_r+\left ( \dfrac{\partial u}{\partial y} \right )_x\left ( \dfrac{\partial y}{\partial \theta} \right )_r\]

Algunos estudiantes encuentran útiles las siguientes construcciones de 'árbol':

Figura\(\PageIndex{2}\): La regla de la cadena (CC BY-NC-SA; Marcia Levitus)

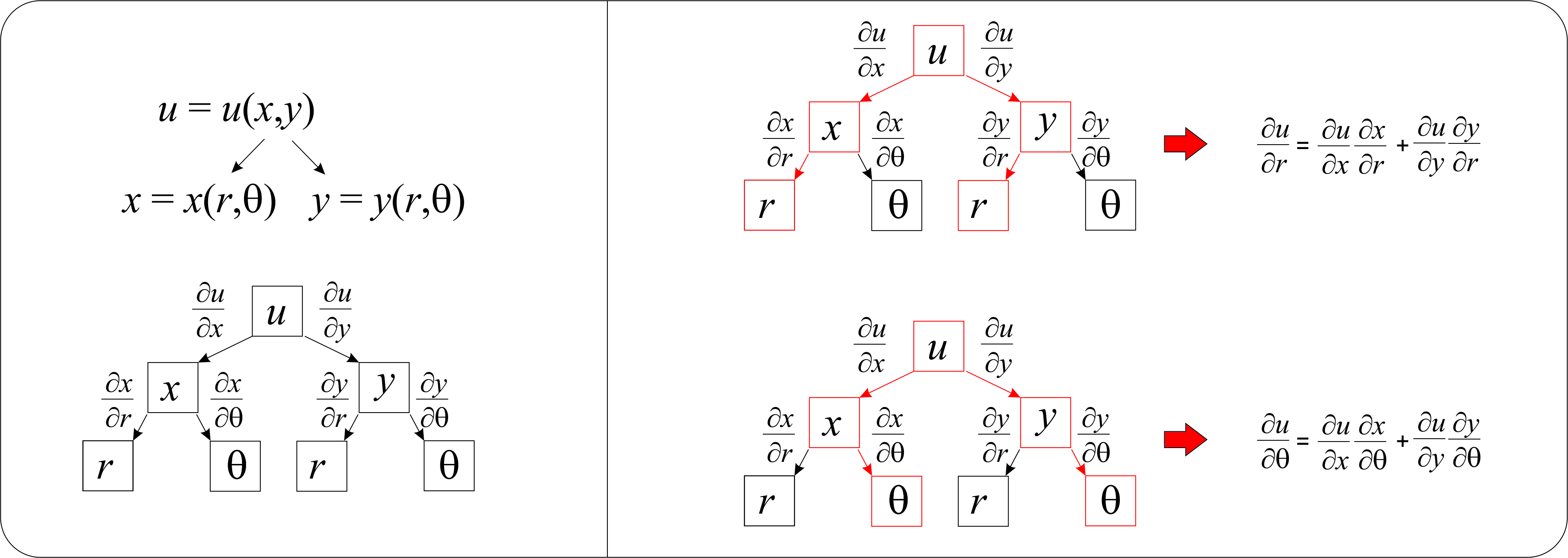
También podemos considerar\(u=u(r,\theta)\), y\(\theta=\theta(x,y)\) y\(r=r(x,y)\), que da:

\[\left ( \dfrac{\partial u}{\partial x} \right )_y=\left ( \dfrac{\partial u}{\partial r} \right )_\theta\left ( \dfrac{\partial r}{\partial x} \right )_y+\left ( \dfrac{\partial u}{\partial \theta} \right )_r\left ( \dfrac{\partial \theta}{\partial x} \right )_y\]

\[\left ( \dfrac{\partial u}{\partial y} \right )_x=\left ( \dfrac{\partial u}{\partial r} \right )_\theta\left ( \dfrac{\partial r}{\partial y} \right )_x+\left ( \dfrac{\partial u}{\partial \theta} \right )_r\left ( \dfrac{\partial \theta}{\partial y} \right )_x\]

Ejemplo\(\PageIndex{1}\)

Derivar Ecuación\ ref {c2v:eq:calculus2v_chain1}.

Solución

Tenemos que probarlo\(\left(\dfrac{\partial f}{\partial x}\right)_y=\cos{\theta}\left(\dfrac{\partial f}{\partial r}\right)_\theta-\dfrac{\sin{\theta}}{r}\left(\dfrac{\partial f}{\partial \theta}\right)_r\). Usando la regla de la cadena:

\[\left ( \dfrac{\partial f}{\partial x} \right )_y=\left ( \dfrac{\partial f}{\partial \theta} \right )_r\left ( \dfrac{\partial \theta}{\partial x} \right )_y+\left ( \dfrac{\partial f}{\partial r} \right )_\theta\left ( \dfrac{\partial r}{\partial x} \right )_y \nonumber\]

De la ecuación\ ref {c2v:eq:calculus2v_cartesiano} y\ ref {c2v:eq:calculus2v_polar}

\[\left ( \dfrac{\partial r}{\partial x} \right )_y=\dfrac{1}{2}(x^2+y^2)^{-1/2}(2x)=\dfrac{1}{2}(r^2)^{-1/2}(2r\cos{\theta})=\cos{\theta} \nonumber\]

\[\left ( \dfrac{\partial \theta}{\partial x} \right )_y=\dfrac{1}{1+(y/x)^2}\dfrac{(-y)}{x^2}=-\dfrac{1}{1+(y/x)^2}\dfrac{y}{x}\dfrac{1}{x}=-\dfrac{1}{1+\tan^2{\theta}}\tan{\theta}\dfrac{1}{r\cos{\theta}}=-\dfrac{1}{1+\dfrac{\sin^2{\theta}}{\cos^2{\theta}}}\dfrac{\sin{\theta}}{\cos{\theta}}\dfrac{1}{r\cos{\theta}}=-\dfrac{\sin{\theta}}{r} \nonumber\]

Por lo tanto,

\[\left ( \dfrac{\partial f}{\partial x} \right )_y=\cos{\theta}\left ( \dfrac{\partial f}{\partial r} \right )_\theta-\dfrac{\sin{\theta}}{r}\left ( \dfrac{\partial f}{\partial \theta} \right )_r \nonumber\]

¿Necesitas ayuda? Los videos a continuación contienen ejemplos de cómo usar la regla de cadena para derivadas parciales:

• Ejemplo 1: http://www.youtube.com/watch?v=HOYA0-pOHsg
• Ejemplo 2: http://www.youtube.com/watch?v=kCr13iTRN7E (diagramas de árbol)