9.5: Integrales de línea

En la Sección 9.1, discutimos que para calcular correctamente el cambio en la presión necesitaríamos integrar el diferencial definido en la Ecuación\ ref {eq:diferenciales1}:

\[dP=\left (\dfrac{\partial P}{\partial V} \right )_{T,n} dV+\left (\dfrac{\partial P}{\partial T} \right )_{V,n} dT \label{eq:differentials1}\]

Esto plantea la cuestión de cómo integrar diferenciales como éste. Antes de enfocarnos en esta pregunta, discutamos qué esperamos para un diferencial exacto. Digamos que sabemos cómo realizar estas integrales, e integramos\(dP\) desde la presión inicial (\(P_i\)) hasta la presión final (\(P_f\)) para calcular\(\Delta P\) para un cambio que no es infinitesimal:

\[ \Delta P = \int_{P_i}^{P_f} dP \nonumber\]

¿Te sorprendería que el resultado sea igual a la presión final menos la presión inicial?

\[ \Delta P = P_f - P_i \nonumber\]

Ojalá que no; el cambio de presión obviamente será la presión final menos la presión inicial, independientemente de si lo hicimos lentamente, rápido, a volumen constante, temperatura constante, etc. En otras palabras, solo necesitas la información del estado del sistema al inicio y al final del proceso , pero no necesitas saber nada de lo que pasó en el medio. Todo esto tiene sentido porque\(P\) es una función de estado, y el mismo argumento se aplica a otras funciones de estado, como la entropía, la energía interna, la energía libre, etc. Acabamos de llegar a una conclusión importante: si integramos un diferencial exacto, el resultado será independiente del camino, y será igual la función en el punto final menos la función en el punto inicial. Si integramos un diferencial inexacto esto no es cierto, porque estaremos integrando el diferencial de una función que no es una función de estado. Volveremos a esto muchas veces, pero es importante que antes de perdernos en las matemáticas tengamos en cuenta qué esperar.

Ya mencionamos la palabra “camino”, pero ¿qué queremos decir con eso? En el ejemplo del gas, la trayectoria estaría descrita por los valores de la temperatura y el volumen en todo momento. Por ejemplo, la Figura\(\PageIndex{1}\) muestra dos posibles trayectorias que dan como resultado el mismo cambio de presión. Podríamos imaginar un número infinito de otras opciones, y por supuesto no estamos restringidos a mantener constante una variable mientras cambiamos la otra.

Figura\(\PageIndex{1}\): Dos caminos diferentes que producen el mismo cambio de presión en un mol de un gas ideal. En el primer caso (rojo), el volumen se comprime de 30 L a 20 L a 250 K, y luego la temperatura se incrementa a 300 K a presión constante. En el segundo caso (verde) la temperatura se eleva primero a 300 K a un volumen constante de 30L, y luego el sistema se comprime a 20L a temperatura constante La superficie azul representa la función\(P=RT/V\) (CC BY-NC-SA; Marcia Levitus)

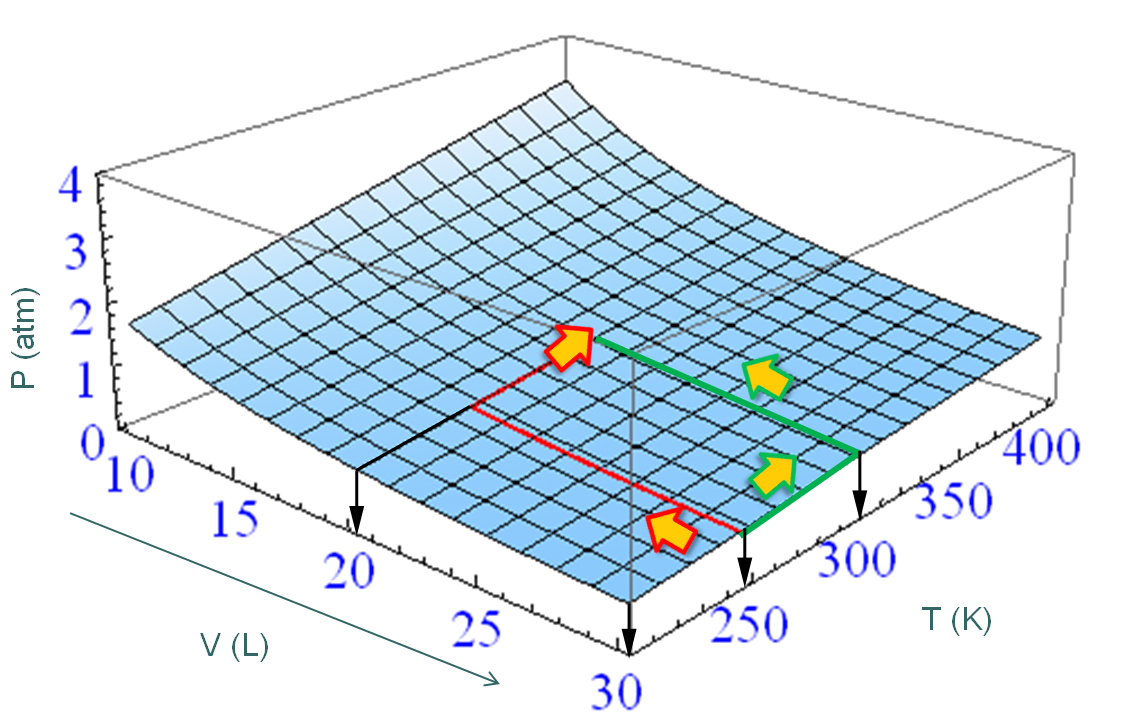
Podemos integrarnos\(dP\) por un camino u otro, pero ya sabemos lo que obtendremos:\(\int dP = P_2-P_1\) independientemente del camino. El trabajo y el calor, por otro lado, no son funciones estatales. No existe tal cosa como una cantidad de trabajo o calor en un sistema. Las cantidades de calor y trabajo que “fluyen” durante un proceso que conecta estados iniciales y finales específicos dependen de cómo se lleve a cabo el proceso. Esto significa que si queremos calcular el trabajo o el calor involucrado en el proceso, necesitaríamos integrar los diferenciales inexactos\(dw\) e\(dq\) indicar la ruta particular utilizada para tomar el sistema desde el estado inicial hasta el final:

\[q=\int\limits_{path} dq \nonumber\]

\[w=\int\limits_{path} dw \nonumber\]

Para un mol de un gas ideal (\(P = RT/V\)),

\[dP=\left (\dfrac{\partial P}{\partial V} \right )_{T,n} dV+\left (\dfrac{\partial P}{\partial T} \right )_{V,n} dT=-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT \nonumber\]

De nuestra discusión anterior, conocemos el resultado de integrar el diferencial

\[dP=-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT \nonumber\]

a lo largo de cualquier camino. El resultado debe ser la presión final menos la presión inicial:

\[\label{eq:diff17} \Delta P=R(T_f/V_f-T_i/V_i)\]

donde los subíndices\(f\) y\(i\) se refieren a los estados final e inicial.

Incluso es que conocemos la respuesta, hagámosla de todas formas para que aprendamos a integrar diferenciales. Consideraremos los dos caminos representados en la Figura\(\PageIndex{1}\). En ambos casos la temperatura inicial es de 250 K, el volumen inicial es de 30 L, la temperatura final es de 300 K y el volumen final es de 20 L.

Empecemos por el camino 'rojo'. Esta ruta es la suma de dos componentes, uno donde cambiamos el volumen a temperatura constante, y otro donde cambiamos la temperatura a volumen constante. Llamemos a estos pasos individuales path 1 y path 2, así que el path total es path1 + path 2:

\[\int\limits_{path}dP=\int\limits_{path 1}dP+\int\limits_{path 2}dP \nonumber\]

\[\int\limits_{path}{\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)}=\int\limits_{path 1}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)+\int\limits_{path 2}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right) \nonumber\]

En el camino 1, mantenemos la temperatura constante, entonces\(dT=0\). Además, la temperatura es igual\(T_i\) durante todo el proceso:

\[\int\limits_{path 1}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int\limits_{path 1}\left(-\dfrac{RT_i}{V^2}dV\right)=\int_{V_i}^{V_f}-\dfrac{RT_i}{V^2}dV \nonumber\]

en el camino 2 mantenemos constante el volumen, entonces\(dV=0\). Además, el volumen es igual\(V_f\) durante todo el proceso:

\[\int\limits_{path 2}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int\limits_{path 2}\dfrac{R}{V_f} dT=\int_{T_i}^{T_f}\dfrac{R}{V_f} dT \nonumber\]

Armando los dos resultados:

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int_{V_i}^{V_f}-\dfrac{RT_i}{V^2}dV+\int_{T_i}^{T_f}\dfrac{R}{V_f} dT \nonumber\]

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\left. \dfrac{RT_i}{V}\right|_{V_i}^{V_f}+\left. \dfrac{RT}{V_f}\right|_{T_i}^{T_f}=RT_i\left(\dfrac{1}{V_f}-\dfrac{1}{V_i}\right)+\dfrac{R}{V_f}(T_f-T_i) \nonumber\]

\[RT_i\left(\dfrac{1}{V_f}-\dfrac{1}{V_i}\right)+\dfrac{R}{V_f}(T_f-T_i)=R\left(\dfrac{T_i}{V_f}-\dfrac{T_i}{V_i}+\dfrac{T_f}{V_f}-\dfrac{T_i}{V_f} \right)=R\left(\dfrac{T_f}{V_f}-\dfrac{T_i}{V_i}\right) \nonumber\]

El resultado es, como se esperaba, idéntico a la Ecuación\ ref {eq:diff17}.

Consideremos ahora el camino de dos pasos representado en verde en la Figura\(\PageIndex{1}\). Seguiremos las mismas ideas que usamos para el camino que se muestra en rojo. En la primera parte del camino cambiamos la temperatura de\(T_i\) a\(T_f\) a volumen constante,\(V=V_i\). En la segunda parte del camino cambiamos el volumen de\(V_i\) a a\(V_f\) temperatura constante,\(T=T_f\). En la primera parte,\(dV=0\) y\(V=V_i\) en todo momento. En la segunda parte,\(dT=0\), y\(T=T_f\) en todo momento:

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int_{T_i}^{T_f}\left(\dfrac{R}{V_i} dT\right)+\int_{V_i}^{V_f}\left(-\dfrac{RT_f}{V^2}dV\right) \nonumber\]

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\left. \dfrac{RT}{V_i}\right|_{T_i}^{T_f}+\left. \dfrac{RT_f}{V}\right|_{V_i}^{V_f} \nonumber\]

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\dfrac{R}{V_i}(T_f-T_i)+RT_f\left(\dfrac{1}{V_f}-\dfrac{1}{V_i}\right)=R\left(\dfrac{T_f}{V_f}-\dfrac{T_i}{V_i}\right) \nonumber\]

El resultado es, como se esperaba,\(P_f-P_i\) (Ecuación\ ref {eq:diff17}).

Porque\(dP\) es exacto, no importa de qué camino elijamos ir\((V_i,P_i)\) a\((V_f,P_f)\), el resultado de la integral de\(dP\) voluntad siempre lo mismo\(R\left(\dfrac{T_f}{V_f}-\dfrac{T_i}{V_i}\right)\). Probemos otro camino; esta vez uno que no mantenga constante ninguna de las variables en ningún momento. Considera el camino que es la línea recta a la que une\((V_i,P_i)\) los puntos\((V_f,P_f)\). Para poder integrarnos a\(dP\) lo largo de un camino particular, necesitamos la ecuación de la ruta que indique cómo\(T\) están conectadas las variables\(V\) y en todo momento.

En este caso,\(T=a+bV\), donde\(a\) está la\(y-\) intercepción y\(b\) es la pendiente. Deberías poder demostrar que los valores de\(a\) y\(b\) para este camino son:

\[ \begin{align*} a&=T_i-\dfrac{T_f-T_i}{V_f-V_i}V_i \\[4pt] b&=\dfrac{T_f-T_i}{V_f-V_i} \end{align*} \nonumber\]

Porque\(T=a+bV\),\(dT=bdV\),\(V=(T-a)/b\), y\(dV=dT/b\). Estas relaciones nos dicen cómo\(T\) y\(V\) están conectadas a lo largo del camino, y por lo tanto podemos escribir estas expresiones equivalentes:

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=-\int_{V_i}^{V_f}\left(-\dfrac{R(a+bV)}{V^2}dV\right)+\int_{T_i}^{T_f}\left(\dfrac{bR}{T-a} dT\right) \nonumber\]

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=-\int_{V_i}^{V_f}\left(-\dfrac{R(a+bV)}{V^2}dV\right)+\int_{V_i}^{V_f}\left(\dfrac{R}{V} bdV\right) \nonumber\]

\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=-\int_{T_i}^{T_f}\left(-\dfrac{RT}{\left[(T-a)/b\right]^2}\dfrac{1}{b}dT\right)+\int_{T_i}^{T_f}\left(\dfrac{bR}{T-a} \right)dT \nonumber\]

En el primer caso acabamos de escribir el primer integrando en términos de\(V\) solo y el segundo integrando en términos de\(T\) solo. Para lograrlo, utilizamos la información del camino para ver cómo\(V\) y\(T\) estamos relacionados a medida que avanzamos de nuestros estados iniciales a nuestros estados finales. La misma idea se aplica a la segunda y tercera línea, donde escribimos todo en términos\(V\) o en términos de\(T\). Las tres ecuaciones darán el mismo resultado independientemente de si el diferencial es exacto en inexacto. No obstante, debido a que estamos integrando un diferencial exacto, el resultado será idéntico al resultado que obtuvimos para los otros dos caminos que comparten el mismo estado inicial y final, y también idéntico al\(P_f-P_i\).

Las tres ecuaciones anteriores no son demasiado difíciles de resolver, pero consumen más tiempo que las integrales que tuvimos que resolver para los caminos que involucran secciones del camino donde una u otra variable permanecen constantes. Esto es poderoso, porque significa que si estás integrando un diferencial exacto, puedes hacerte inteligente y resolver la integral para un camino muy fácil, siempre y cuando los estados inicial y final sean los mismos. Sabes que el resultado será el mismo porque el diferencial es exacto. Si, por otro lado, el diferencial es inexacto, no tenemos suerte. La integral depende del camino, por lo que necesitamos resolver el camino que se nos da.

Porque\(dP\) es exacto, la integral de línea es igual\(P_f-P_i\). Una consecuencia de esto es que la integral a lo largo de un camino cerrado (uno donde\(P_i=P_f\)) es cero. Matemáticamente:

\[\oint dP=0 \nonumber\]

donde el círculo dentro del símbolo de integración significa que el camino está cerrado. Esto es cierto para cualquier diferencial exacto, pero no necesariamente cierto para un diferencial que es inexacto. Volviendo a la termodinámica, imagina un mol de un gas en un contenedor cuyo volumen primero se reduce de 30 L a 20 L a una temperatura constante T= 250 K. Luego calienta el gas hasta 300 K manteniendo constante el volumen, luego vuelve a aumentar el volumen a 30 L manteniendo la temperatura constante, y finalmente enfriarlo hasta 250 K a volumen constante (ver Figura\(\PageIndex{1}\). Debido a que los estados inicial y final son los mismos, la integral de línea de cualquier función de estado es cero:

\[\Delta P=\oint dP=0 \nonumber\]

\[\Delta G= \oint dG= 0 \nonumber\]

\[\Delta S =\oint dS=0 \nonumber\]

etc, etc

Esta trayectoria cerrada no implica un cambio de presión, energía libre o entropía, porque estas funciones son funciones de estado, y el estado final es idéntico al estado inicial.

Por otra parte,

\[w=\oint dw\neq0 \nonumber\]

\[q= \oint dq\neq 0 \nonumber\]

porque estamos integrando diferenciales inexactos. Físicamente, había que hacer trabajos para expandir el gas, calentarlo, comprimirlo, enfriarlo, etc. no importa que termines exactamente donde empezaste, el trabajo y el calor estuvieron involucrados en el proceso. Puede ser posible que un camino cerrado en particular ceda\(w=0\) o\(q=0\), pero en general esto no necesita ser el caso.

Ejemplo\(\PageIndex{1}\)

Dado el siguiente diferencial\(dz=x\;dy+2y\;dx\), y el camino cerrado que se muestra en la figura, calcular la integral de línea\(\int\limits_{path}dz\)

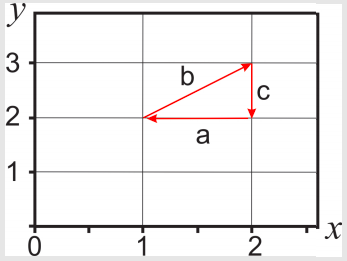
Nota: Este problema también está disponible en formato de video: http://tinyurl.com/mszuwr7

Solución

El camino se divide en tres secciones, por lo que

\[\int\limits_{path}dz= \int_{a}dz+ \int_{b}dz+ \int_{c}dz \nonumber\]

En la sección\(a\):\(y=2\),\(dy=0\) (\(y\)es una constante), y\(x\) cambia de un valor inicial de 2 a un valor final de 1:

\[\int_{a}dz=\int_{2}^1 4 dx=4x\left. \right|_{2}^1=4-8=-4 \nonumber\]

En la sección\(b\):\(y=1+x\)\(dy=dx\),, y\(x\) cambia de un valor inicial de 1 a un valor final de 2:

\[\int_{b}dz=\int_{b}x\;dy+2y\;dx=\int_{1}^{2} x\; dx+\int_{1}^2 2(1+x) \;dx=\left.\dfrac{x^2}{2}\right|_{1}^{2}+2\left.\dfrac{(1+x)^2}{2}\right|_{1}^{2}=\dfrac{3}{2}+(9-4)=\dfrac{13}{2} \nonumber\]

En la sección\(c\):\(x=2\),\(dx=0\) (\(x\)es una constante), y\(y\) cambia de un valor inicial de 3 a un valor final de 2:

\[\int_{c}dz=\int_{3}^2 2 dy=2y\left. \right|_{3}^2=4-6=-2 \nonumber\]

Por lo tanto,

\[\int\limits_{path}dz= \int_{a}dz+ \int_{b}dz+ \int_{c}dz=-4+13/2-2=\displaystyle{\color{Maroon}1/2} \nonumber\]

Observe que la integral no es cero aunque el camino estuviera cerrado. Esto no es sorprendente dado que el diferencial fue inexacto.

Ejemplo\(\PageIndex{2}\)

Considerar el diferencial

\[du=(x^2-y^2)dx+(2xy)dy \nonumber\]

1. ¿Es\(du\) exacto o inexacto?
2. Explique por qué cada uno de los siguientes es verdadero o falso:
   • \(du\)es el diferencial total de alguna función\(u(x,y)\). Encuentra\(u(x,y)\) si es posible.
   • \(\int_{a}du= \int_{b}du= \int_{c}du\)siempre\(a,b\) y cuando y\(c\) sean caminos en el\((x,y)\) espacio que comparten los mismos puntos de inicio y fin.
3. Calcular\(\int\limits_{path}du\) si el camino es la línea recta que une los puntos (0,2) y (2,0).

Solución:

Para probar si\(du\) es exacta o inexacta, comparamos las siguientes derivadas

\[\left(\dfrac{\partial (x^2-y^2)}{\partial y} \right )_x\overset{?}{=}\left(\dfrac{\partial (2xy)}{\partial x} \right )_y \nonumber \]

Debido a que las dos derivadas parciales no son iguales, el diferencial es inexacto.

Debido a que el diferencial es inexacto, no es el diferencial total de una función\(u(x,y)\). No podemos encontrar la función porque no existe.

Las integrales de línea\(\int_{a}du, \int_{b}du\) y\(\int_{c}du\) serán en principio diferentes porque la integral de un diferencial inexacto depende no sólo de los estados inicial y final, sino también de la ruta utilizada para llegar del estado inicial al final. El enunciado sería cierto para un diferencial exacto.

Para calcular la integral a lo largo de la línea recta que une los puntos (0,2) y (2,0), primero necesitamos encontrar la ecuación\(y(x)\) que describe este camino. Dibujar la función no es imprescindible, pero podría ayudar:

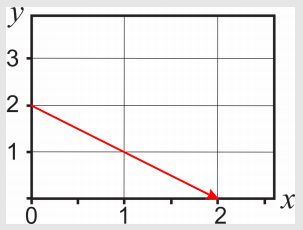
La ecuación de esta recta es\(y=2-x\). Por lo tanto, a lo largo del camino,\(y=2-x\) y\(dy=-dx\). La variable\(x\) cambia de un valor inicial\(x=0\) a un valor final\(x=2\):

\[\int\limits_{path}du=\int\limits_{path}(x^2-y^2)dx+(2xy)dy \nonumber\]

Es importante recalcar que\(x\) y no\(y\) son independientes a lo largo del proceso, sino que están conectados a través de la ecuación del camino. Escribiremos la ecuación en términos de\(x\) (podríamos hacerlo en términos de\(y\) con resultados idénticos):

\[ \begin{align*} \int\limits_{path}du &=\int\limits_{path}(x^2-y^2)dx+(2xy)dy \\[4pt] &=\int_{0}^2(x^2-(2-x)^2)dx+\int_{0}^2(2x(2-x))(-dx) \\[4pt] &=\int_{0}^2(x^2-(4+x^2-4x))dx-\int_{0}^2(4x-2x^2)dx \\[4pt] &=\int_{0}^2(4x-4)dx-\int_{0}^2(4x-2x^2)dx=\int_{0}^2(2x^2-4)dx \\[4pt] &=\left. \left(\dfrac{2x^3}{3}-4x\right)\right|_{0}^{2}=\dfrac{16}{3}-8=-\dfrac{8}{3} \\[4pt] &=\displaystyle{\color{Maroon}-\dfrac{8}{3}} \end{align*} \nonumber\]