12.3: La ecuación de onda en una dimensión
- Page ID
- 69844
La ecuación de onda es una ecuación diferencial parcial lineal importante de segundo orden que describe ondas tales como ondas sonoras, ondas de luz y ondas de agua. En este curso, nos centraremos en las oscilaciones en una dimensión. Consideremos una cadena delgada de longitud\(l\) que se fija en sus dos puntos finales, y llamemos al desplazamiento de la cadena desde su posición horizontal\(u(x,t)\) (figure [fig:pde1]). El desplazamiento de cada punto de la cadena se limita a una dimensión, pero debido a que el desplazamiento también depende del tiempo, la ecuación de onda unidimensional es una PDE:
\[\label{eq:pde10} \dfrac{\partial^2u(x,t)}{\partial x^2}=\dfrac{1}{v^2}\dfrac{\partial^2 u(x,t)}{\partial t^2}\]
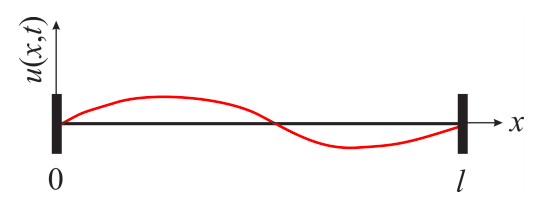
Debido a que la cadena se mantiene en ambos extremos, la PDE está sujeta a dos condiciones de límite:
\[\label{eq:pde11} u(0,t)=u(l,t)=0\]
Utilizando el método de separación de variables, asumimos que la función\(u(x,t)\) puede escribirse como el producto de una función de solo\(x\) y una función de solo\(t\).
\[\label{eq:pde12} u(x,t)=f(x)g(t)\]
Sustituyendo la ecuación\ ref {eq:pde12} en la ecuación\ ref {eq:pde10}:
\[\dfrac{\partial^2f(x)g(t)}{\partial x^2}=\dfrac{1}{v^2}\dfrac{\partial^2 f(x)g(t)}{\partial t^2} \nonumber\]
\[\label{eq:pde13} g(t)\dfrac{\partial^2 f(x)}{\partial x^2}=\dfrac{1}{v^2}f(x)\dfrac{\partial^2 g(t)}{\partial t^2}\]
y separar los términos\(x\) de los términos en\(y\):
\[\label{eq:pde14} \dfrac{1}{f(x)}\dfrac{\partial^2 f(x)}{\partial x^2}=\dfrac{1}{v^2}\dfrac{1}{g(t)}\dfrac{\partial^2 g(t)}{\partial t^2}\]
Recuerda que\(v\) es una constante, y podríamos dejarla a ambos lados de la Ecuación\ ref {eq:pde14}. El lado izquierdo de esta ecuación es una función de\(x\) solo, y el lado derecho es una función de\(t\) solo. Porque\(x\) y\(t\) son variables independientes, la única manera que sostiene la igualdad es que cada lado sea igual a una constante.
\[\dfrac{1}{f(x)}\dfrac{\partial^2 f(x)}{\partial x^2}=\dfrac{1}{v^2}\dfrac{1}{g(t)}\dfrac{\partial^2 g(t)}{\partial t^2}=K \nonumber\]
\(K\)se llama la constante de separación, y será determinada por las condiciones de límite. Tenga en cuenta que después de la separación de variables, una PDE se convirtió en dos ODE:
\[\label{eq:pde15a} \dfrac{1}{f(x)}\dfrac{\partial^2 f(x)}{\partial x^2}=K\rightarrow \dfrac{\partial^2 f(x)}{\partial x^2}-Kf(x)=0\]
\[\label{eq:pde15b} \dfrac{1}{v^2}\dfrac{1}{g(t)}\dfrac{\partial^2 g(t)}{\partial t^2}=K\rightarrow \dfrac{\partial^2 g(t)}{\partial t^2}-Kv^2g(t)=0\]
Ambas son ecuaciones diferenciales ordinarias de segundo orden con coeficientes constantes, por lo que podemos resolverlas usando los métodos que aprendimos en el Capítulo 5.
De la ecuación\ ref {eq:pde15a},
\[\dfrac{\partial ^2f(x)}{\partial x^2}-Kf(x)=0 \nonumber\]
que es una ODE de 2do orden con ecuación auxiliar
\[\alpha^2-K=0\Rightarrow \alpha=\pm\sqrt{K} \nonumber\]
y por lo tanto
\[\label{eq:pde16} f(x)=c_1e^{\sqrt{K}x}+c_2e^{-\sqrt{K}x}\]
Aún no sabemos si\(K\) es positivo, negativo o cero, por lo que no sabemos si se trata de exponenciales reales o complejos. Usaremos las condiciones de contorno (\(f(0)=f(l)=0\)) y veremos qué sucede:
\[f(x)=c_1e^{\sqrt{K}x}+c_2e^{-\sqrt{K}x}\rightarrow f(0)=c_1+c_2=0\Rightarrow c_1=-c_2 \nonumber\]
\[f(x)=c_1(e^{\sqrt{K}x}-e^{-\sqrt{K}x})\rightarrow f(l)=c_1(e^{\sqrt{K}l}-e^{-\sqrt{K}l})=0 \nonumber\]
Hay dos formas de hacer
\[f(l)=c_1(e^{\sqrt{K}l}-e^{-\sqrt{K}l})=0. \nonumber\]
Podríamos elegir\(c_1=0\), pero esta elección resultaría en\(f(x)=0\), lo que físicamente significa que la cuerda no está vibrando en absoluto (el desplazamiento de todos los puntos es cero). Esta es sin duda una solución matemáticamente aceptable, pero no es una solución que represente el comportamiento físico de nuestra cadena. Por lo tanto, la única opción viable es\(e^{\sqrt{K}l}=e^{-\sqrt{K}l}\). Veamos qué significa esto en términos de\(K\). No hay ningún valor positivo de\(K\) que hace
\[e^{\sqrt{K}l}=e^{-\sqrt{K}l}. \nonumber\]
Si\(K=0\), obtenemos\(f(x)=0\), lo que de nuevo no es físicamente aceptable. Entonces, el valor de\(K\) tiene que ser negativo, y\(\sqrt{K}\) es un número imaginario:
\[e^{\sqrt{K}l}=e^{-\sqrt{K}l} \nonumber\]
\[e^{i\sqrt{|K|}l}=e^{-i\sqrt{|K|}l} \nonumber\]
donde\(|K|=-K\) está el valor absoluto de\(K<0\). Usando la relación de Euler:
\[\cos(\sqrt{|K|}l)+i\sin(\sqrt{|K|}l)=\cos(\sqrt{|K|}l)-i\sin(\sqrt{|K|}l) \nonumber\]
\[2i\sin(\sqrt{|K|}l)=0\rightarrow \sqrt{|K|}l=n\pi\rightarrow \sqrt{|K|}=\left( \dfrac{n\pi}{l}\right) \nonumber\]
Ahora que tenemos una expresión para\(K\), podemos escribir una expresión para\(f(x)\):
\[f(x)=c_1(e^{\sqrt{K}x}-e^{-\sqrt{K}x})=c_1(e^{i\sqrt{|K|}x}-e^{-i\sqrt{|K|}x})=2ic_1\sin(\sqrt{|K|}x) \nonumber\]
\[\label{eq:pde17} f(x)=A\sin\left(\dfrac{n\pi}{l}x\right)\]
Hasta ahora llegamos\(f(x)\), así que tenemos que seguir adelante y obtener una expresión para\(g(t)\) de la ecuación\ ref {eq:pde15b}. Observe, sin embargo, que ahora conocemos el valor de\(K\), así que volvamos a escribir la ecuación\ ref {eq:pde15b} como:
\[\label{eq:pde 18} \dfrac{\partial^2 g(t)}{\partial t^2}+\left(\dfrac{n\pi}{l}\right)^2v^2g(t)=0\]
Esta es otra ODE de 2do orden, con ecuación auxiliar
\[\alpha^2+\left(\dfrac{n\pi}{l}\right)^2v^2=0\rightarrow \alpha=\pm i \left( \dfrac{n\pi}{l} v\right) \nonumber\]
entonces podemos escribir\(g(t)\) como:
\[g(t)=c_1e^{i \left( \dfrac{n\pi}{l} v\right) t}+c_2e^{-i \left( \dfrac{n\pi}{l} v\right) t} \nonumber\]
que deberías poder probar puede ser reescrito como
\[\label{eq:pde_19} g(t)=c_3\sin \left( \dfrac{n\pi}{l} vt\right) +c_4\cos \left( \dfrac{n\pi}{l} vt\right)\]
No podemos obtener los valores de\(c_3\) y\(c_4\) sin embargo porque no tenemos información sobre las condiciones iniciales. Antes de discutir esto, sin embargo, juntemos las dos piezas:
\[u(x,t)=\sin \left( \dfrac{n\pi}{l}x \right) \left[p_n\sin \left( \dfrac{n\pi}{l} vt\right) +q_n\cos \left( \dfrac{n\pi}{l} vt\right) \right] \nonumber\]
donde combinamos las constantes\(A\) y\(c_{1,2}\) y las renombramos\(p_n\) y\(q_n\). Los subíndices enfatizan el hecho de que estas constantes dependen\(n\), lo que será importante en un minuto. Antes de seguir adelante, y para simplificar la notación, reconozcamos que la cantidad\(\dfrac{n \pi v}{l}\) tiene unidades de tiempo recíproco. Esto es cierto porque necesita dar un número adimensional cuando se multiplica por\(t\). Esto quiere decir que, físicamente,\(\dfrac{n \pi v}{l}\) representa una frecuencia, por lo que podemos llamarla\(\omega_n\):
\[\label{eq:pde_20} u(x,t)=\sin \left( \dfrac{n\pi}{l}x \right) \left[p_n\sin \left(\omega_nt\right) +q_n\cos \left(\omega_nt\right) \right]\;n=1,2,...,\infty\]
En este punto, reconocemos que tenemos un número infinito de soluciones:
\[\label{eq:pde_21} u_1(x,t)=\sin \left( \dfrac{\pi}{l}x \right) \left[p_1\sin \left(\omega_1t\right) +q_1\cos \left(\omega_1 t\right) \right]\]
\[u_2(x,t)=\sin \left( 2\dfrac{\pi}{l}x \right) \left[p_2\sin \left(\omega_2t\right) +q_2\cos \left(\omega_2t\right) \right] \nonumber\]
\[\vdots \nonumber\]
\[u_n(x,t)=\sin \left( n\dfrac{\pi}{l}x \right) \left[p_n\sin \left(\omega_nt\right) +q_n\cos \left(\omega_nt\right) \right] \nonumber\]
donde\(\omega_1, \omega_2,...,\omega_n=\dfrac{\pi v}{l},\dfrac{2\pi v}{l},...,\dfrac{n\pi v}{l}\). Como es habitual, la solución general es una combinación lineal de todas estas soluciones:
\[\label{eq:pde_22} u(x,t)=c_1u_1(x,t)+c_2u_2(x,t)+...+c_nu_n(x,t)={\color{red}\sum_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) \left[a_n\sin \left(\omega_nt\right) +b_n\cos \left(\omega_nt\right) \right]}\]
dónde\(a_n=c_np_n\) y\(b_n=c_nq_n\).
Observe que aún no hemos utilizado ninguna condición inicial. Utilizamos las condiciones de límite que nos dieron (\(u(0,t)=u(l,t)=0\)), por lo que la ecuación\ ref {eq:pde_22} es válida independientemente de las condiciones iniciales siempre y cuando la cadena se mantiene fija en ambos extremos. Como puede sospechar, los valores de\(a_n\) y se\(b_n\) calcularán a partir de las condiciones iniciales. No obstante, observe que para poder describir el movimiento de la cadena en todo momento necesitaremos calcular un número infinito de\(a_n\) -valores y un número infinito de\(b_n\) -valores. Esto suena bastante intimidante, pero verás cómo todo el tiempo que pasaste aprendiendo sobre las series de Fourier finalmente dará sus frutos. Antes de investigar cómo hacerlo, echemos un vistazo a las soluciones individuales enumeradas en la ecuación\ ref {eq:pde_21}.
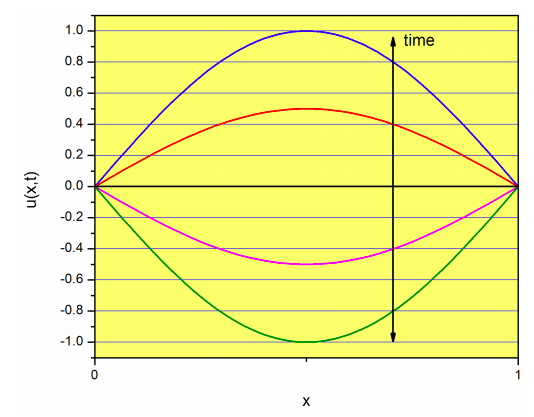
Cada uno\(u_n(x,t)\) se llama modo normal. Por ejemplo, para\(n=1\), tenemos
\[u_1(x,t)=\sin \left( \dfrac{\pi}{l}x \right) \left[p_1\sin \left(\omega_1t\right) +q_1\cos \left(\omega_1t\right) \right] \nonumber\]
que se llama el modo fundamental, o primer armónico.
Observe que esta función es producto de una función que depende únicamente de\(x\) (\(\sin \left( \dfrac{\pi}{l}x \right)\)) y otra función que depende únicamente de\(t\), es decir,
\[\left[p_1\sin \left(\omega_1t\right) +q_1\cos \left(\omega_1t\right) \right]. \nonumber\]
La función on\(t\) simplemente cambia la amplitud de la función sinusoidal en\(x\):
Para\(n=2\), contamos con:
\[u_2(x,t)=\sin \left( 2\dfrac{\pi}{l}x \right) \left[p_2\sin \left(\omega_2t\right) +q_2\cos \left(\omega_2t\right) \right] \nonumber\]
que se llama el primer armónico, o segundo armónico. Nuevamente, esta función es producto de una función que depende de\(x\) only (\(\sin \left( 2\dfrac{\pi}{l}x \right)\)), y otra que depende\(t\) y cambia la amplitud de\(\sin \left( 2\dfrac{\pi}{l}x \right)\) sin cambiar su forma general:
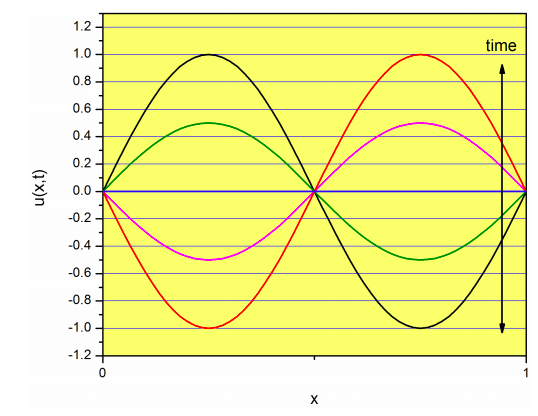
Para\(n=3\), contamos con:
\[u_3(x,t)=\sin \left( 3\dfrac{\pi}{l}x \right) \left[p_3\sin \left(\omega_3t\right) +q_3\cos \left(\omega_3t\right) \right] \nonumber\]
que se llama el segundo armónico, o tercer armónico. Nuevamente, esta función es producto de una función que depende de\(x\) only (\(\sin \left( 3\dfrac{\pi}{l}x \right)\)), y otra que depende\(t\) y cambia la amplitud de\(\sin \left( 3\dfrac{\pi}{l}x \right)\) sin cambiar su forma general:
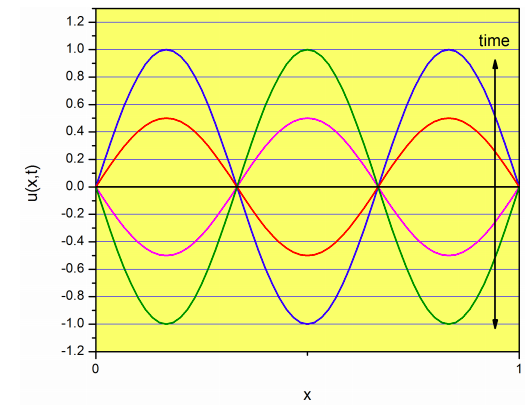
Si la forma inicial de la cadena (es decir, la función\(u(x,t)\) en el tiempo cero) es\(\sin \left( \dfrac{\pi}{l}x \right)\) (Figura\(\PageIndex{2}\), entonces la cuerda vibrará como se muestra en la figura, simplemente cambiando la amplitud pero no la forma general. En términos más generales, si\(u(x,0)\) es uno de los modos normales, la cuerda vibrará de acuerdo a ese modo normal, sin mezclarse con el resto. Sin embargo, en general, la forma de la cadena se describirá mediante una combinación lineal de modos normales (Ecuación\ ref {eq:pde_22}). Si recuerdas del Capítulo 7, una serie de Fourier te dice cómo expresar una función como una combinación lineal de senos y cosenos. La idea aquí es la misma: expresaremos una forma arbitraria como una combinación lineal de modos normales, que son una colección de funciones sinusoidales.
Para hacer eso, necesitamos información sobre la forma inicial:\(u(x,0)\). También necesitamos información sobre la velocidad inicial de todos los puntos de la cadena:\(\dfrac{\partial u(x,0)}{\partial t}\). La forma inicial es el desplazamiento de todos los puntos en el tiempo cero, y es una función de\(x\). Llamemos a esta función\(y_1(x)\):
\[\label{eq:pde23} u(x,0)=y_1(x)\]
La velocidad inicial de todos los puntos también es una función de\(x\), y la llamaremos\(y_2(x)\):
\[\label{eq:pde24} \dfrac{\partial u(x,0)}{\partial t}=y_2(x)\]
Ambas funciones juntas representan las condiciones iniciales, y serán utilizadas para calcular todos los\(b_n\) coeficientes\(a_n\) y. Para simplificar el problema, supongamos que en el tiempo cero mantenemos la cadena quieta, por lo que la velocidad de todos los puntos es cero:
\[\dfrac{\partial u(x,0)}{\partial t}=0 \nonumber\]
Veamos cómo podemos usar esta información para terminar el problema (es decir, calcular los coeficientes\(a_n\) y\(b_n\)). De Ecuaciones\ ref {eq:pde_22} y\ ref {eq:pde23}:
\[u(x,t)=\sum_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) \left[a_n\sin \left(\omega_nt\right) +b_n\cos \left(\omega_nt\right) \right] \nonumber\]
y aplicando la primera condición inicial:
\[\label{eq:pde_25} u(x,0)=\sum_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) [b_n]=y_1(x)\]
Esta ecuación nos dice que la forma inicial,\(y_1(x)\), puede describirse como una suma infinita de funciones sinusoidales... ¿suena familiar? En el Capítulo 7, vimos que podemos representar una función impar periódica\(f(x)\) del período\(2L\) como una suma infinita de funciones sinusoidales (Ecuación\(7.2.1\),\( f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}a_n \cos\left ( \dfrac{n\pi x}{L} \right )+\sum_{n=1}^{\infty}b_n \sin\left ( \dfrac{n\pi x}{L} \right )\)):
\[\label{eq:pde_26} f(x)=\sum_{n=1}^{\infty}b_n sin\left ( \dfrac{n\pi x}{L} \right )\]
Comparando las Ecuaciones\ ref {eq:pde_25} y\ ref {eq:pde_26}, vemos que para calcular los\(b_n\) coeficientes de la Ecuación\ ref {eq:pde_22}, necesitamos crear una extensión impar de\(y_1\) con periodo\(2l\).
Veamos cómo funciona esto con un ejemplo. Supongamos que el desplazamiento inicial viene dado por la función que se muestra en la figura:
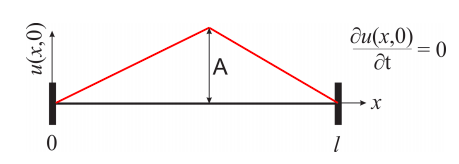
La ecuación\ ref {eq:pde_25} nos dice que la función de Figura se\(\PageIndex{5}\) puede expresar como una suma infinita de funciones sinusoidales. Si averiguamos qué suma, tendremos los coeficientes que\(b_n\) necesitamos para anotar la expresión de que\(u(x,y)\) estamos buscando (Ecuación\ ref {eq:pde_22}). Todavía necesitaremos los coeficientes\(a_n\), que se calcularán a partir de la segunda condición inicial (Ecuación\ ref {eq:pde24}).
Porque sabemos que la suma infinita de la Ecuación\ ref {eq:pde_25} describe una función periódica impar de punto\(2l\), nuestro primer paso es extender de una\(y_1(x)\) manera impar:
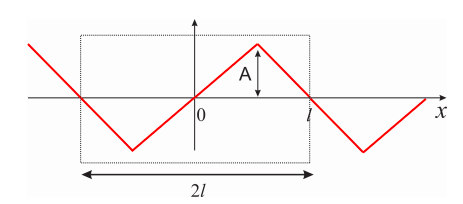
¿Cuál es la serie de Fourier de la función periódica de Figura\(\PageIndex{6}\)? Utilizando los métodos que aprendimos en el Capítulo 7, obtenemos:
\[\label{eq:pde_27} y_1(x)=\dfrac{8A}{\pi^2}\left[\sin \dfrac{\pi x}{l}- \dfrac{1}{3^2}\sin\dfrac{3\pi x}{l} + \dfrac{1}{5^2}\sin\dfrac{5\pi x}{l}... \right]=\dfrac{8A}{\pi^2} \sum\limits_{n=0}^{\infty}\dfrac{(-1)^n}{(2n+1)^2} \sin \left( \dfrac{(2n+1)\pi}{l}x \right)\]
De la ecuación\ ref {eq:pde_25}
\(u(x,0)=\sum\limits_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) [b_n]=y_1(x)\)
comparando Ecuaciones\ ref {eq:pde_25} y\ ref {eq:pde_27}:
\[\label{eq:pde_28} b_n = \begin{cases} 0& n=2,4,6... \\ \dfrac{8A}{\pi^2n^2} & n=1,5,9... \\ - \dfrac{8A}{\pi^2n^2} & n=3,7,11... \end{cases}\]
¡Genial! tenemos todos los coeficientes\(b_n\), así que estamos a un paso de nuestro objetivo final de expresar\(u(x,t)\). Nuestro último paso es calcular los coeficientes\(a_n\). Utilizaremos la última condición inicial:\(\dfrac{\partial u(x,0)}{\partial t}=y_2(x)\). Tomando la derivada parcial de la ecuación\ ref {eq:pde_22}:
\[u(x,t)=\sum\limits_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) \left[a_n\sin \left(\omega_nt\right) +b_n\cos \left(\omega_nt\right) \right] \nonumber\]
\[\dfrac{\partial u(x,t)}{\partial t}=\sum\limits_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) \left[a_n\omega_n\cos \left(\omega_nt\right) -b_n\omega_n\sin \left(\omega_nt\right) \right] \nonumber\]
\[\label{eq:pde_29} \dfrac{\partial u(x,0)}{\partial t}=\sum\limits_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) \left[a_n\omega_n\right]=y_2(x)\]
La ecuación\ ref {eq:pde_29} nos dice que la función\(y_2(x)\) puede expresarse como una suma infinita de funciones sinusoidales. Nuevamente, necesitamos crear una extensión impar de\(y_2(x)\) y obtener su serie de Fourier:\(y_2(x)=\sum_{n=1}^{\infty}b_n sin\left ( \dfrac{n\pi x}{L} \right )\). Los coeficientes\(b_n\) de la serie de Fourier son iguales\(a_n\omega_n\) (Ecuación\ ref {eq:pde_29}). En este caso particular:
\[\dfrac{\partial u(x,0)}{\partial t}=\sum\limits_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) \left[a_n\omega_n\right]=0\rightarrow a_n=0 \nonumber\]
Los coeficientes\(a_n\) son cero, porque la derivada necesita ser cero para todos los valores de\(x\).
Ahora que tenemos todos los coeficientes\(b_n\) y\(a_n\) estamos listos para concluir esto. De Ecuaciones\ ref {eq:pde_22} y\ ref {eq:pde_28}:
\[\begin{align} u(x,t) &=\sum\limits_{n=1}^{\infty}\sin \left( \dfrac{n\pi}{l}x \right) \left[a_n\sin \left(\omega_nt\right) +b_n\cos \left(\omega_nt\right) \right] \\[4pt] &=b_1\sin \left( \dfrac{\pi}{l}x \right)\cos \left( \omega_1t \right)+b_3\sin \left( \dfrac{3\pi}{l}x \right)\cos \left( \omega_3t \right)+b_5\sin \left( \dfrac{5\pi}{l}x \right)\cos \left( \omega_5t \right)... \\[4pt] &=\dfrac{8A}{\pi^2}\left[\sin \left( \dfrac{\pi}{l}x \right)\cos \left( \omega_1t \right)-\dfrac{1}{3^2}\sin \left( \dfrac{3\pi}{l}x \right)\cos \left( \omega_3t \right)+\dfrac{1}{5^2}\sin \left( \dfrac{5\pi}{l}x \right)\cos \left( \omega_5t \right)...\right] \end{align} \nonumber\]
Recordando que\(\omega_n=\dfrac{n\pi}{l}v\):
\[u(x,t)=\dfrac{8A}{\pi^2}\left[\sin \left( \dfrac{\pi}{l}x \right)\cos \left( \dfrac{\pi }{l}vt \right)-\dfrac{1}{3^2}\sin \left( \dfrac{3\pi}{l}x \right)\cos \left( \dfrac{3\pi }{l}vt \right)+\dfrac{1}{5^2}\sin \left( \dfrac{5\pi}{l}x \right)\cos \left(\dfrac{5\pi }{l}vt \right)...\right] \nonumber\]
\[\label{eq:pde_30} {\color{Maroon}u(x,t)=\dfrac{8A}{\pi^2}\sum\limits_{n=0}^{\infty}\dfrac{(-1)^n}{(2n+1)^2}\sin \left( \dfrac{(2n+1)\pi}{l}x \right) \cos \left(\dfrac{(2n+1)\pi }{l}vt \right)}\]
¡Éxito! Tenemos una descripción completa del movimiento de la cuerda. Solo necesitamos conocer la longitud de la cadena (\(l\)), el desplazamiento inicial del punto medio (\(A\)) y el parámetro\(v\), y podemos comenzar a trazar la forma de la cadena en diferentes momentos. Solo recuerda que Mathematica no puede trazar una función definida como una suma infinita, por lo que tendrás que trazar una versión truncada de Equation\ ref {eq:pde_30}. Como es habitual, cuantos más términos incluyas mejor será la aproximación, pero cuanto más tiempo tardará la computadora en ejecutar el comando. Para ver una increíble película en cámara lenta de una cadena real sigue este enlace de youtube.
El parámetro\(v\) tiene unidades de longitud a lo largo del tiempo (por ejemplo, m/s), y depende de factores como el material de la cuerda, su tensión y su grosor. Un instrumento de cuerda como una guitarra, por ejemplo, tiene cuerdas hechas de diferentes materiales, y sostenidas a diferentes tensiones. Al ser arrancados, producen vibraciones de diferentes frecuencias, que percibimos como diferentes notas musicales. En general, la vibración de la cuerda será una combinación lineal de los modos normales de los que hablamos anteriormente en esta sección. Cada modo normal tiene una frecuencia única (\(\omega_n=\dfrac{n\pi}{l}v\)), y si esta frecuencia está dentro de nuestro rango audible, la percibiremos como una nota musical pura. Una combinación lineal de modos normales contiene muchas frecuencias, y las percibimos como un sonido más complejo.
La música es agradable, pero ¿qué pasa con las aplicaciones de los modos normales en química? Ya mencionamos vibraciones moleculares en diferentes capítulos, y sabemos que los átomos en las moléculas están continuamente vibrando siguiendo movimientos aproximadamente armónicos. De la misma manera que la vibración de la cuerda de la Figura se\(\PageIndex{5}\) puede expresar como una combinación lineal de todos los modos normales (Figuras\(\PageIndex{2}\) -\(\PageIndex{4}\), podemos expresar las vibraciones de una molécula poliatómica como una combinación lineal de modos normales. Como verás en tus cursos avanzados de química física, una molécula poliatómica no lineal tiene modos\(3n-6\) vibracionales normales, donde\(n\) está el número de átomos. Para la molécula de agua, por ejemplo, tenemos 3 modos normales:
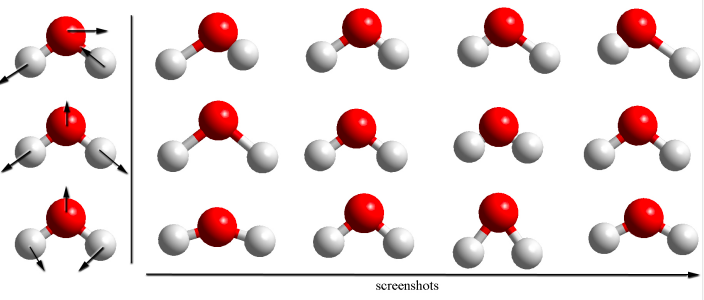
Cualquier otro tipo de vibración se puede expresar como una combinación lineal de estos tres modos normales. Como puedes imaginar, estos movimientos ocurren muy rápido. Normalmente, se puede ver del orden de\(10^{12}\) las vibraciones por segundo. La forma más directa de sondear las vibraciones de una molécula es a través de la espectroscopia infrarroja, y de hecho medirás y analizarás los espectros vibracionales de moléculas simples en tus laboratorios de química física de 300 niveles.

