12.4: Difusión Molecular
- Page ID
- 69842
La difusión molecular es el movimiento térmico de las moléculas a temperaturas superiores al cero absoluto. La velocidad de este movimiento es una función de la temperatura, viscosidad del fluido y el tamaño y forma de las partículas. La difusión explica el flujo neto de moléculas de una región de mayor concentración a una de menor concentración. El término “difusión” también se usa generalmente para describir el flujo de otras cantidades físicas. Por ejemplo, la difusión de la energía térmica (calor) es descrita por la ecuación de calor, que es matemáticamente idéntica a la ecuación de difusión que consideraremos en esta sección.
Para visualizar lo que entendemos por difusión molecular, considere un tinte rojo que se difunde en un tubo de ensayo. Supongamos que el experimento comienza colocando una muestra del tinte en una capa delgada a mitad del tubo. La difusión ocurre porque todas las moléculas se mueven debido a su energía térmica. Cada molécula se mueve en una dirección aleatoria, lo que significa que si esperas lo suficiente, las moléculas terminarán siendo distribuidas aleatoriamente por todo el tubo. Esto significa que hay un movimiento neto de moléculas de tinte desde áreas de alta concentración (la banda central) hacia áreas de baja concentración (Figura\(\PageIndex{1}\). La velocidad de difusión depende de la temperatura, el tamaño y la forma de las moléculas y la viscosidad del disolvente.
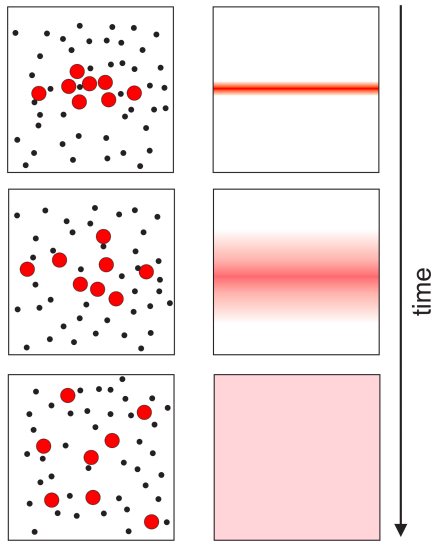
La ecuación de difusión que describe cómo cambia la concentración de soluto (en este caso el tinte rojo) con la posición y el tiempo es:
\[\label{eq:pde31} \nabla^2C(\mathbf{r},t)=\frac{1}{D}\frac{\partial C(\mathbf{r},t)}{\partial t}\]
donde\(\mathbf{r}\) es un vector que representa la posición en un sistema de coordenadas particular. Esta ecuación se conoce como la segunda ley de difusión de Fick, y su solución depende de la dimensionalidad del problema (1D, 2D, 3D), y de las condiciones iniciales y límite. Si las moléculas son capaces de moverse en una sola dimensión (por ejemplo, en un tubo que es mucho más largo que su diámetro):
\[\label{eq:pde32} \frac{\partial^2C(x,t)}{\partial x^2}=\frac{1}{D}\frac{\partial C(x,t)}{\partial t}\]
Supongamos que el tubo tiene una longitud\(L\) y está cerrado en ambos extremos. Matemáticamente, esto significa que el flujo de moléculas en\(x = 0\) y\(x = L\) es cero. El flujo se define como el número de moles de sustancia que atraviesan un\(1 m^2\) área por segundo, y se define matemáticamente como
\[\label{eq:pde33} J=-D\frac{\partial C(x,t)}{\partial x}\]
Si el tubo está cerrado, las moléculas en\(x=0\) no pueden moverse del lado derecho al lado izquierdo, y las moléculas en\(x=L\) no pueden moverse del lado izquierdo al lado derecho. Matemáticamente:
\[\label{eq:pde34} \frac{\partial C(0,t)}{\partial x}=\frac{\partial C(L,t)}{\partial x}=0\]
Estas serán las condiciones límite que usaremos para resolver el problema Todavía necesitamos una condición inicial, que en este caso es el perfil de concentración inicial:\(C(x,0)=y(x)\). Observe que debido a la conservación masiva, la integral de\(C(x)\) debe ser constante en todo momento. No vamos a usar esto para resolver el problema, pero podemos verificar que la solución satisface este requisito.
Independientemente de las condiciones iniciales, el perfil de concentración se expresará como (Problema 12.3):
\[\label{eq:pde_35} C(x,t)=\sum\limits_{n=0}^{\infty}a_n\cos\left(\frac{n\pi}{L}x \right)e^{-\left(\frac{n\pi}{L}\right)^2Dt}\]
Para calcular los coeficientes\(a_n\), necesitamos información sobre el perfil de concentración inicial:\(C(x,0)=y(x)\).
\[\label{eq:pde_36} C(x,0)=\sum\limits_{n=0}^{\infty}a_n\cos\left(\frac{n\pi}{L}x \right)=y(x)\]
Esta expresión nos dice que la función\(y(x)\) puede expresarse como una suma infinita de cosenos. Sabemos por el Capítulo 7 que una suma infinita de cosenos como este representa una función periódica par de período\(2L\), por lo que para encontrar los coeficientes\(a_n\), necesitamos construir la extensión incluso periódica de la función\(y(x)\) y encontrar su serie de Fourier. Por ejemplo, supongamos que el perfil de concentración inicial viene dado por la Figura\(\PageIndex{2}\). Imagina que tienes agua en la mitad derecha del tubo, y una solución 1M de tinte rojo en el medio lado izquierdo. En el tiempo cero, eliminas la barrera que separa las dos mitades, y observas cómo evoluciona la concentración en función del tiempo. Antes de calcular estos perfiles de concentración, pensemos en lo que esperamos en tiempos muy largos, cuando se permite que el tinte se mezcle completamente con el agua. Sabemos que el mismo número de moléculas presentes inicialmente necesitan ser redistribuidas en toda la longitud del tubo, por lo que el perfil de concentración debe ser constante a 0.5M. Es una buena idea que esboces lo que imaginas que sucede en el medio antes de pasar por las matemáticas y ver los resultados.
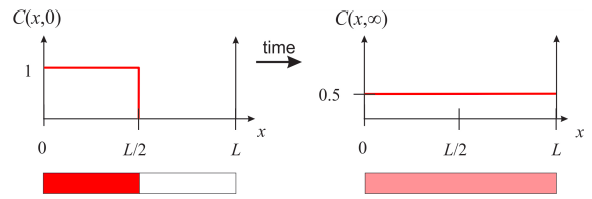
Para calcular los coeficientes\(a_n\) que necesitamos para completar la Ecuación\ ref {eq:pde_35}, necesitamos expresarnos\(C(x,0)\) como una suma infinita de funciones coseno, y por lo tanto necesitamos la extensión par de la función:
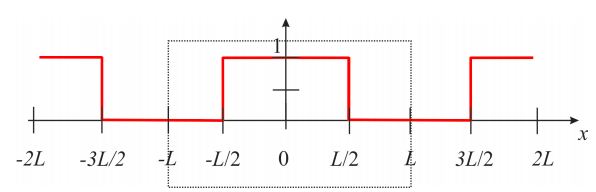
Calculemos la serie de Fourier de esta función periódica de periodo\(2L\) (Ecuación\(7.2.1\),\( f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}a_n \cos\left ( \dfrac{n\pi x}{L} \right )+\sum_{n=1}^{\infty}b_n \sin\left ( \dfrac{n\pi x}{L} \right )\)).
\[f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n cos\left ( \frac{n\pi x}{L} \right ) \nonumber\]
\[a_0=\frac{1}{L}\int_{-L}^{L}f(x)dx \nonumber\]
\[a_n=\frac{1}{L}\int_{-L}^{L}f(x)\cos{\left(\frac{n\pi x}{L} \right)}dx \nonumber\]
Supongamos\(L=1cm\) (usaremos\(D\) en unidades de\(cm^2/s\) y\(t\) en segundos):
\[a_0=\frac{1}{L}\int_{-L}^{L}f(x)dx=\int_{-1/2}^{1/2}1dx=1 \nonumber\]
\[a_n=\int_{-1/2}^{1/2}1\cos{\left(n\pi x\right)}dx=\frac{1}{n\pi}\left.\begin{matrix}\sin(n\pi x)\end{matrix}\right|_{-1/2}^{1/2}=\frac{1}{n\pi}[\sin{(n\pi/2)}-\sin{(-n\pi/2)}] \nonumber\]
porque\(\sin{x}\) es impar:
\[a_n=\frac{2}{n\pi}\sin{(n\pi/2)}\rightarrow a_1=\frac{2}{\pi}, a_2=0, a_3=-\frac{2}{3\pi}, a_4=0, a_5=\frac{2}{5\pi}... \nonumber \]
y por lo tanto:
\[C(x,0)=\frac{1}{2}+\frac{2}{\pi}\sum\limits_{n=0}^{\infty}(-1)^{n}\frac{1}{2n+1}\cos{[(2n+1)\pi x]} \nonumber\]
y la descripción completa de\(C(x,t)\) es (Ecuación\ ref {eq:pde_35}):
\[\label{eq:pde_37} C(x,t)=\frac{1}{2}+\frac{2}{\pi}\sum\limits_{n=0}^{\infty}(-1)^{n}\frac{1}{2n+1}\cos{[(2n+1)\pi x]}e^{-[(2n+1)\pi]^2Dt}\]
Vamos\(C(x,t)\) a trazar en diferentes momentos asumiendo\(L=1cm\) y\(D=6.5 \times 10^{-6}cm^2 s^{-1}\), que es el coeficiente de difusión de la sacarosa (azúcar regular) en el agua.
Observe que la derivada\(\frac{\partial C(x,t)}{\partial x}\) es cero en ambos\(x=0\) y\(x=L=1cm\) en todo momento, como debería ser el caso dadas las condiciones de contorno. Además, el área bajo la curva es constante debido a la conservación masiva. Además, ¡fíjate cuánto tiempo tarda la difusión en mezclar las dos mitades del tubo! Tomaría alrededor de un día para que la concentración sea relativamente homogénea en un tubo de 1 cm, lo que explica por qué es una buena idea remover el azúcar de tu café con una cuchara en lugar de esperar a que la difusión haga el trabajo. La difusión es ineficiente porque las moléculas se mueven en direcciones aleatorias, y cada vez que se topan con una molécula de agua cambian de dirección. Imagina que necesitas caminar desde la esquina de Apache y Rural hasta la esquina de College y University Ave, y cada vez que das un paso lanzas un dado de cuatro lados para decidir si te mueves al sur, norte, este u oeste. Eventualmente podrías llegar a tu destino, pero es probable que te lleve mucho tiempo.


