12.5: Problemas

Problema\(\PageIndex{1}\)

Encuentra\(f(x, y)\). Nota: Para obtener todas las soluciones posibles en cada caso habrá que considerar que la constante de separación puede ser positiva, negativa o cero.

1. \(2 \frac{ \partial f}{ \partial x} + \frac{ \partial f}{ \partial y} = 0\)
2. \(y \frac{ \partial f}{ \partial x} − x \frac{ \partial f}{ \partial y} = 0\)
3. \( \frac{\partial^2 f}{ \partial x^2} + \frac{\partial^2 f}{\partial y^2} = 0\)

Problema\(\PageIndex{2}\)

Considera una cuerda uniforme bajo tensión y longitud\(L\). En\(t = 0\) el momento la cuerda se desplaza como se muestra en la figura y se libera. El desplazamiento de la cuerda desde su posición horizontal\((u(x, t))\) depende de ambos\(x\)\(t\) y satisface los siguientes PDE:

\[ \frac{ \partial^2 u(x, t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 u(x, t)}{\partial t^2}\]

donde\(v\) es una constante que depende de las características de la cadena.

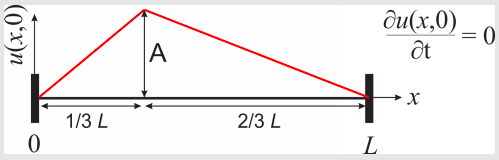
1. Obtener una expresión para\(u(x, t)\). Tenga en cuenta que la mayor parte del problema se resuelve en el libro, pero aún necesita mostrar TODOS los pasos.
2. En el laboratorio: Asumir\(v = 440 \text{m/s}, ~ A = 5 \text{cm}\) y\(L = 12 \text{cm}\). Crear una función\(u(x, t)\) con el resultado de 1). Recuerda que no puedes trazar una suma infinita, así que tendrás que truncarla al trazar en Mathematica. Usa la función “Manipulate” para generar una animación de la cuerda vibratoria. Asegúrese de ejecutarlo lentamente para que pueda ver el movimiento).

Problema\(\PageIndex{3}\)

Utilizar el método de separación de variables para obtener una expresión\(C(x, t)\) para el sistema descrito en la Sección 12.4:

\[ \frac{\partial^2 C(x,t)}{\partial x^2} = \frac{1}{D} \frac{\partial C(x,t)}{\partial t} \nonumber\]

\[\frac{\partial C(0,t)}{\partial x} = \frac{\partial C(L,t)}{\partial x} = 0 \nonumber\]

La solución es:

\[ C(x, t) = \sum_{n=0}^{\infty} a_n \cos \left( \frac{n \pi}{L} x \right)e^{− \left( \frac{n \pi}{L} \right)^2 Dt} \nonumber\]

donde los coeficientes\(a_n\) dependen del perfil de concentración inicial (condiciones iniciales).

Problema\(\PageIndex{4}\)

Continuar con el problema anterior y obtener la expresión completa de\(C(x, t)\) usar la condición inicial que se muestra en la Figura\(\PageIndex{1}\):

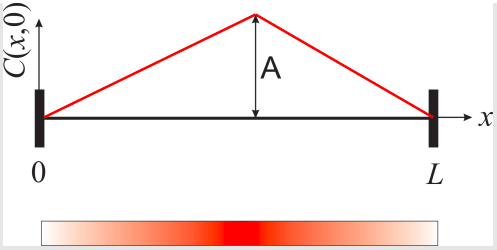
Figura\(\PageIndex{1}\): El perfil de concentración inicial,\(C(x, 0)\). El diagrama en la parte inferior representa una caricatura de cómo se vería el tubo en el tiempo cero, con mayor concentración de tinte rojo en el centro y concentración cero en ambos extremos.

La extensión uniforme de esta función es (comparar con la Figura\(12.3.6\))

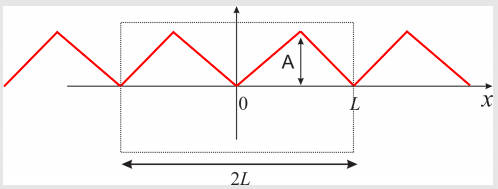
Figura\(\PageIndex{2}\): La extensión uniforme de y (x) (Figura\(\PageIndex{1}\)).

En el laboratorio:

• Asumir\(L = 1 \text{cm}, ~ A = 1 \text{M}\), y\(D = 6.510−10\text{m}^2/\text{s}\) (el coeficiente de difusión de la glucosa en el agua) Use Manipulate para crear una película que muestre cómo\(C(x)\) cambia con el tiempo.
• Trazar\(C(0, t)\) (es decir, la concentración al final del tubo en función del tiempo). ¿Cuánto tiempo tarda hasta que la concentración alcanza los 0.1M? (dar un valor aproximado). Esto debería demostrar la necesidad de remover su café después de agregar azúcar (es decir, esperar hasta que el azúcar se difunda por sí solo tardaría demasiado en disfrutar de una taza de café caliente).
• Repetir la pregunta anterior asumiendo\(L = 1 \mu \text{m}\) (el orden de magnitud del diámetro del núcleo de una célula). Esto debería demostrar que la difusión es un mecanismo eficiente para el transporte molecular dentro de células pequeñas como bacterias, o dentro del núcleo de células más grandes.