13.4: Propiedades de los Determinantes
- Page ID
- 69994
1-
\[\label{eq:identity} \begin{vmatrix} 1 &0&0 \\ 0&1 &0 \\ 0& 0 &1 \end{vmatrix}=1\]
Esto es cierto en cualquier dimensión, y se puede entender fácilmente a partir de argumentos geométricos. En dos dimensiones, las columnas representan vectores unitarios a lo largo del\(y\) eje\(x\) y, por lo tanto, el paralelogramo es un cuadrado de área unitaria. En tres dimensiones, las columnas representan vectores unitarios a lo largo del\(z\) eje\(x\),\(y\) y, por lo tanto, la caja es un cubo de volumen unitario.
2-
Antisimetría: Si se intercambian dos filas (o dos columnas) de un determinante, el valor del determinante se multiplica por -1. Esta propiedad es extremadamente útil en mecánica cuántica, por lo que vale la pena recordarla!
\[\label{eq:determinants4} \begin{vmatrix} a &b & c \\ d &e &f \\ g &h &i \end{vmatrix}=- \begin{vmatrix} b&a &c \\ e&d &f\\ h &g &i \end{vmatrix}=- \begin{vmatrix} d&e &f \\ a &b &c\\ g &h &i \end{vmatrix}\]
Ya discutimos esta propiedad en dos dimensiones (ver Figura\(13.3.3\)).
3-
Los escalares pueden ser factorizados a partir de filas y columnas.
\[\label{eq:determinants5} \begin{vmatrix} a&b &c \\ \lambda d &\lambda e &\lambda f\\ g &h&i \end{vmatrix} = \lambda \begin{vmatrix} a &b & c \\ d &e &f \\ g &h &i \end{vmatrix}\]
Geométricamente hablando, si multiplicas la longitud de uno de los bordes del paralelepípedo por\(\lambda\), el volumen también se multiplica por\(\lambda\).
4-
Regla de adición: Si todos los elementos de cualquier fila (o columna) se escriben como la suma de dos términos, entonces el determinante puede escribirse como la suma de dos determinantes
\[\label{eq:determinants6} \begin{vmatrix} a+b&c &d \\ e+f &g &h\\ i+j &k &l \end{vmatrix} = \begin{vmatrix} a&c & d \\ e& g &h\\ i&k &l \end{vmatrix} + \begin{vmatrix} b&c &d \\ f& g &h\\ j&k &l \end{vmatrix}\]
\[\label{eq:determinants6b} \begin{vmatrix} a+b&c+d &e+f \\ g &h &i\\ j &k &l \end{vmatrix}= \begin{vmatrix} a&c & e \\ g &h &i\\ j &k &l \end{vmatrix}+ \begin{vmatrix} b&d &f \\ g &h &i\\ j &k &l \end{vmatrix}\]
5-
El valor de un determinante es cero si dos filas o dos columnas son iguales. Esto es consecuencia de la propiedad 2. Intercambiar las dos filas idénticas se supone que cambia el signo del determinante, pero sabemos que intercambiar dos filas idénticas no le hace nada al determinante. Por lo tanto, el determinante tiene que ser cero.
Geométricamente, dos bordes de la caja serían iguales, renderizando una caja plana sin volumen.
\[\label{eq:determinants3} \begin{vmatrix} {\color{red}a} &{\color{Red}a} &{\color{Blue} b} \\ {\color{red}c} &{\color{red}c} &{\color{Blue}d} \\ {\color{red}e} &{\color{red}e} &{\color{Blue}f} \end{vmatrix}=0\]
6-
El valor de un determinante no cambia si una fila o columna se suma o se resta a otra. Esta propiedad es consecuencia de las propiedades 4 y 5:
\[\label{eq:determinants7} \begin{vmatrix} a+b&b &c \\ d+e & e & f\\ g+h &h &i \end{vmatrix}= \begin{vmatrix} a&b &c \\ d&e& f\\ g&h&i \end{vmatrix}+ \begin{vmatrix} b&b&c \\ e&e& f\\ h&h&i \end{vmatrix}\]
7-
Un caso especial de propiedad 3 es que si todos los elementos de una fila o columna son cero, el valor del determinante es cero. En términos geométricos, si uno de los bordes es un punto, el volumen es cero.
\[\label{eq:determinants6extra} \begin{vmatrix} a &b &c \\ 0 &0 &0 \\ d &e &f \end{vmatrix}=0\]
8-
El valor de un determinante es cero si una fila (o columna) es un múltiplo de otra fila (o columna). Geométricamente, esto significa que dos bordes del paralelepípedo se encuentran en la misma línea, y por lo tanto el volumen es cero. Esto es consecuencia de las propiedades 3 y 5:
\[\label{eq:determinants8} \begin{vmatrix} a&b &c \\ \lambda a &\lambda b &\lambda c\\ d &e &f \end{vmatrix}= \lambda\begin{vmatrix} a&b & c\\ a &b&c \\ d&e &f \end{vmatrix}=0\]
9-
Transposición: el valor del determinante no cambia si se intercambian sus filas y columnas. Esta propiedad se puede derivar de las propiedades anteriores, aunque es un poco complicado para el nivel de este curso.
\[\label{eq:determinants2} \begin{vmatrix} {\color{red}a}&{\color{OliveGreen}b} &{\color{Blue} c} \\ {\color{red}d} &{\color{OliveGreen}e} &{\color{Blue}f} \\ {\color{red}g} &{\color{OliveGreen}h} &{\color{Blue}i} \end{vmatrix}= \begin{vmatrix} {\color{red}a} &{\color{red}d} &{\color{red}g} \\ {\color{OliveGreen}b} &{\color{OliveGreen}e} &{\color{OliveGreen}h} \\ {\color{Blue}c}& {\color{Blue}f}&{\color{Blue}i} \end{vmatrix}\]
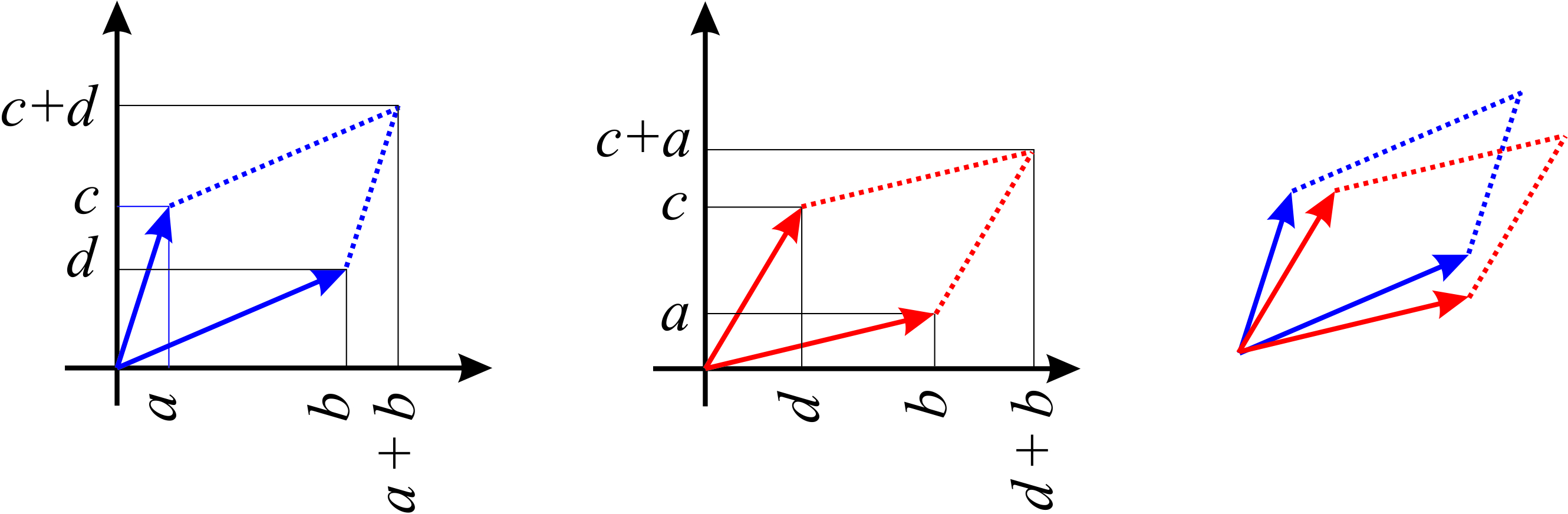
Geométricamente, el intercambio de filas por columnas gira el paralelogramo (o la caja en 3D) sin cambiar el área (o el volumen). La figura\(\PageIndex{1}\) muestra que
\[\begin{vmatrix}b &a\\ d& c \end{vmatrix}=\begin{vmatrix}b &d\\ a& c \end{vmatrix} \nonumber\]
Ejemplo\(\PageIndex{1}\)
Determinar el valor del siguiente determinante mediante inspección.
\[\begin{vmatrix} 2&6 &1 \\ -4 &4 &-2\\ 2 &-3 &1 \end{vmatrix} \nonumber\]
Solución
Notamos que la tercera columna es un múltiplo de la primera:
\[\begin{align*} \begin{vmatrix} 2&6 &1 \\ -4 &4 &-2\\ 2 &-3 &1 \end{vmatrix} &= \begin{vmatrix} 1\times 2&6 &1 \\ -2 \times 2 &4 &-2\\ 1 \times 2 &-3 &1 \end{vmatrix} \\[4pt] &=2\times \begin{vmatrix} 1&6 &1 \\ -2 &4 &-2\\ 1 &-3 &1 \end{vmatrix} \\[4pt] &=\displaystyle{\color{Maroon}0} \end{align*} \nonumber\]
El determinante es cero porque dos de sus columnas son iguales.

