1.27: Espectroscopia - Interacción de Átomos y Moléculas con la Luz

En nuestra aplicación final de la teoría de grupos, investigaremos la manera en que las consideraciones de simetría influyen en la interacción de la luz con la materia. Ya hemos utilizado la teoría de grupos para aprender sobre los orbitales moleculares en una molécula. En esta sección mostraremos que también se puede utilizar para predecir a qué estados electrónicos se puede acceder por absorción de un fotón. También podemos usar la teoría de grupos para investigar cómo se puede usar la luz para excitar los diversos modos vibracionales de una molécula poliatómica.

El año pasado, te introdujeron a la espectroscopia en el contexto de las transiciones electrónicas en átomos. Aprendiste que un fotón de la energía apropiada es capaz de excitar una transición electrónica en un átomo, sujeto a las siguientes reglas de selección:

\[\begin{array}{rcl} \Delta n & = & \text{integer} \\ \Delta l & = & \pm 1 \\ \Delta L & = & 0, \pm 1 \\ \Delta S & = & 0 \\ \Delta J & = & 0, \pm 1; J=0 \not \leftrightarrow J=0 \end{array} \tag{27.1}\]

Lo que quizás no hayas aprendido es de dónde vienen estas reglas de selección. En general, diferentes tipos de transición espectroscópica obedecen diferentes reglas de selección. Las transiciones que has encontrado hasta ahora implican cambiar el estado electrónico de un átomo, e implican la absorción de un fotón en la parte UV o visible del espectro electromagnético. Existen transiciones electrónicas análogas en las moléculas, las cuales consideraremos con más detalle en breve. La absorción de un fotón en la región infrarroja (IR) del espectro conduce a la excitación vibracional en las moléculas, mientras que los fotones en la región de microondas (MW) producen excitación rotacional. Cada tipo de excitación obedece a sus propias reglas de selección, pero el procedimiento general para determinar las reglas de selección es el mismo en todos los casos. Es simplemente determinar las condiciones bajo las cuales la probabilidad de una transición no es idéntica a cero.

Por lo tanto, el primer paso para comprender los orígenes de las reglas de selección debe ser aprender cómo se calculan las probabilidades de transición. Esto requiere de alguna mecánica cuántica.

El año pasado aprendiste sobre operadores, valores propios y funciones propias en la mecánica cuántica. Sabes que si una función es una función propia de un operador en particular, entonces operar en la función propia con el operador devolverá lo observable asociado a ese estado, conocido como el valor propio (es decir\(\hat{A} \Psi = a \Psi\) ). Lo que quizás no sepas es que operar en una función que NO es una función propia del operador conduce a un cambio en el estado del sistema. En las transiciones que estaremos considerando, la molécula interactúa con el campo eléctrico de la luz (a diferencia de la espectroscopia de RMN, en la que los núcleos interactúan con el campo magnético de la radiación electromagnética). Estas transiciones se llaman transiciones dipolares eléctricas, y el operador que nos interesa es el operador dipolo eléctrico, generalmente dado el símbolo\(\hat{\boldsymbol{\mu}}\), which describes the electric field of the light.

Si empezamos en algún estado inicial\(\Psi_i\), operando en este estado con\(\hat{\boldsymbol{\mu}}\) gives a new state, \(\Psi = \hat{\boldsymbol{\mu}} \Psi\). Si queremos conocer la probabilidad de terminar en algún estado final particular\(\Psi_f\), la amplitud de probabilidad viene dada simplemente por la integral de superposición entre\(\Psi\) y\(\Psi_f\). Esta amplitud de probabilidad se llama el momento dipolar de transición, y se le da el símbolo\(\boldsymbol{\mu}_{fi}\) _. .

\[\hat{\boldsymbol{\mu}}_{fi} = \langle\Psi_f | \Psi\rangle = \langle\Psi_f | \hat{\boldsymbol{\mu}} | \Psi_i\rangle \tag{27.2}\]

Físicamente, el momento dipolar de transición puede pensarse como describiendo la 'patada' que el electrón recibe o imparte al campo eléctrico de la luz a medida que experimenta una transición. La probabilidad de transición viene dada por el cuadrado de la amplitud de probabilidad.

\[P_{fi} = \hat{\boldsymbol{\mu}}_{fi}^2 = |\langle\Psi_f | \hat{\boldsymbol{\mu}} | \Psi_i\rangle|^2 \tag{27.3}\]

Ojalá quede claro que para determinar las reglas de selección para una transición dipolar eléctrica entre estados\(\Psi_i\) y\(\Psi_f\), necesitamos encontrar las condiciones bajo las cuales\(\boldsymbol{\mu}_{fi}\) puede ser distinto de cero. Una forma de hacer esto sería escribir las ecuaciones para las dos funciones de onda (que son funciones de los números cuánticos que definen los dos estados) y el operador de momento dipolo eléctrico, y simplemente pasar por las integrales. Al examinar el resultado, entonces sería posible decidir qué restricciones deben imponerse a los números cuánticos de los estados inicial y final para que se permita una transición, dando lugar a reglas de selección del tipo enumerado anteriormente para los átomos. Sin embargo, muchas reglas de selección pueden derivarse con mucho menos trabajo, basadas simplemente en consideraciones de simetría.

En la sección\(17\), we showed how to use group theory to determine whether or not an integral may be non-zero. This forms the basis of our consideration of selection rules.

Transiciones electrónicas en moléculas

Supongamos que tenemos una molécula en algún estado inicial\(\Psi_i\). Queremos determinar a qué estados finales se\(\Psi_f\) puede acceder por absorción de un fotón. Recordemos que para que una integral sea distinta de cero, la representación para el integrando debe contener la representación irreducible totalmente simétrica. La integral que queremos evaluar es

\[\hat{\boldsymbol{\mu}}_{fi} = \int \Psi_f^* \hat{\boldsymbol{\mu}} \Psi_i d\tau \tag{27.4}\]

por lo que necesitamos determinar la simetría de la función\(\Psi_f^* \hat{\boldsymbol{\mu}} \Psi_i\). Como aprendimos en Sección\(18\), the product of two functions transforms as the direct product of their symmetry species, so all we need to do to see if a transition between two chosen states is allowed is work out the symmetry species of \(\Psi_f\),\(\hat{\boldsymbol{\mu}}\) and \(\Psi_i\), tomar su producto directo, y ver si contiene la representación irreducible totalmente simétrica para el grupo puntual de interés. Equivalentemente (como se explica en la Sección\(18\)), we can take the direct product of the irreducible representations for \(\hat{\boldsymbol{\mu}}\) and \(\Psi_i\) y ver si contiene la representación irreducible para\(\Psi_f\) . Esto se ilustra mejor usando un par de ejemplos.

Anteriormente en el curso, aprendimos a determinar los orbitales moleculares de simetría. La simetría de un estado electrónico se encuentra identificando cualquier electrón desapareado y tomando el producto directo de las representaciones irreducibles de los orbitales moleculares en los que se encuentran. El estado fundamental de una molécula de caparazón cerrado, en la que todos los electrones están emparejados, siempre pertenece a la representación irreducible totalmente simétrica\(^7\). A modo de ejemplo, el estado básico electrónico de\(NH_3\), que pertenece al grupo de\(C_{3v}\) puntos, tiene\(A_1\) simetría. Para saber a qué estados electrónicos se puede acceder por absorción de un fotón, necesitamos determinar las representaciones irreducibles para el operador de dipolo eléctrico\(\hat{\boldsymbol{\mu}}\). La luz que se polariza linealmente a lo largo de\(z\) los ejes\(x\)\(y\),, y se transforma de la misma manera que las funciones\(x\)\(y\), y\(z\) en la tabla de caracteres\(^8\). De la tabla de\(C_{3v}\) personajes, vemos que\(x\) - y\(y\) -la luz polarizada se transforma como\(E\), mientras que\(z\) -la luz polarizada se transforma como\(A_1\). Por lo tanto:

1. Para\(x\)- or \(y\)-polarized light, \(\Gamma_\hat{\boldsymbol{\mu}} \otimes \Gamma_{\Psi 1}\) transformarse como luz\(E \otimes A_1 = E\). This means that absorption of \(x\)- or \(y\)- polarizada por\(NH_3\) (see figure below left) will excite the molecule to a state of \(E\) simetría de estado fundamental.
2. Para\(z\)-polarized light, \(\Gamma_\hat{\boldsymbol{\mu}} \otimes \Gamma_{\Psi 1 }\) transforma como\(A_1 \otimes A_1 = A_1\). Absorción del\(z\)-polarized light by ground estado\(NH_3\) (see figure below right) will excite the molecule to a state of \(A_1\) symmetry.

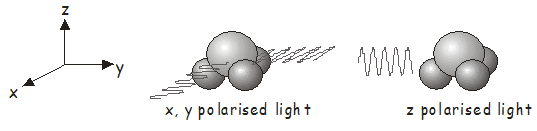
Por supuesto, los fotones también deben tener la energía adecuada, además de tener la polarización correcta para inducir una transición.

Podemos realizar el mismo análisis para\(H_2O\), which belongs to the \(C_{2v}\) point group. We showed previously that \(H_2O\) has three molecular orbitals of \(A_1\) symmetry, two of \(B_1\) symmetry, and one of \(B_2\) symmetry, with the ground state having \(A_1\) symmetry. In the \(C_{2v}\) point group, \(x\)-polarized light has \(B_1\) symmetry, and can therefore be used to excite electronic states of this symmetry; \(y\)-polarized light has \(B_2\) symmetry, and may be used to access the \(B_2\) excited state; and \(z\)-polarized light has \(A_1\) symmetry, and may be used to access higher lying \(A_1\) states. Consider our previous molecular orbital diagram for \(H_2O\).

El estado fundamental electrónico tiene dos electrones en a\(B_2\) orbital, giving a state of \(A_1\) symmetry (\(B_2 \otimes B_2 = A_1\)). El primer estado electrónico excitado tiene la configuración\((1B_2)^1(3A_1)^1\) and its symmetry is \(B_2 \otimes A_1 = B_2\). Se puede acceder desde el estado base por un\(y\)-polarized photon. The second excited state is accessed from the ground state by exciting an electron to the \(2B_1\) orbital. It has the configuration \((1B_2)^1(2B_1)^1\), its symmetry is \(B_2 \otimes B_1 = A_2\). Ya que ni\(x\)-, \(y\)- or \(z\)-polarized light transforms as \(A_2\), this state may not be excited from the ground state by absorption of a single photon.

Transiciones vibracionales en moléculas

Consideraciones similares se aplican para las transiciones vibracionales. Luz polarizada a lo largo del\(x\), \(y\), and \(z\) axes of the molecule may be used to excite vibrations with the same symmetry as the \(x\), \(y\) and \(z\) functions listed in the character table.

Por ejemplo, en el\(C_{2v}\) point group, \(x\)-polarized light may be used to excite vibrations of \(B_1\) symmetry, \(y\)-polarized light to excite vibrations of \(B_2\) symmetry, and \(z\)-polarized light to excite vibrations of \(A_1\) symmetry. In \(H_2O\), we would use \(z\)-polarized light to excite the symmetric stretch and bending modes, and \(x\)-polarized light to excite the asymmetric stretch. Shining \(y\)-polarized light onto a molecule of \(H_2O\) would not excite any vibrational motion.

Dispersión Raman

Si hay modos vibracionales en la molécula a los que no se puede acceder usando un solo fotón, aún puede ser posible excitarlos usando un proceso de dos fotones conocido como dispersión Raman\(^9\). A continuación se muestra un diagrama de nivel de energía para la dispersión Raman.

El primer fotón excita la molécula a algún estado intermedio alto, conocido como estado virtual. Los estados virtuales no son verdaderos estados estacionarios de la molécula (es decir, no son funciones propias del Hamiltoniano molecular), pero pueden considerarse como estados estacionarios del sistema de 'molécula de fotón + '. Este tipo de estados tienen una vida extremadamente corta, y rápidamente emitirán un fotón para devolver el sistema a un estado molecular estable, que puede ser diferente del estado original. Dado que hay dos fotones (uno absorbido y otro emitido) involucrados en la dispersión Raman, que pueden tener diferentes polarizaciones, el dipolo de transición para una transición Raman se transforma como uno de los productos cartesianos\(x^2\), \(y^2\), \(z^2\), \(xy\), \(xz\), \(yz\) listed in the character tables.

Los modos vibracionales que se transforman como uno de los productos cartesianos pueden ser excitados por una transición Raman, de la misma manera que los modos que se transforman como\(x\), \(y\), or \(z\) may be excited by a one-photon vibrational transition.

En\(H_2O\), all of the vibrational modes are accessible by ordinary one-photon vibrational transitions. However, they may also be accessed by Raman transitions. The Cartesian products transform as follows in the \(C_{2v}\) point group.

\[\begin{array}{clcl} A_1 & x^2, y^2, z^2 & B_1 & xz \\ A_2 & sy & B_2 & yz \end{array} \tag{27.5}\]

El estiramiento simétrico y la vibración de flexión del agua, ambos de\(A_1\) symmetry, may therefore be excited by any Raman scattering process involving two photons of the same polarization (\(x\)-, \(y\)- or \(z\)-polarized). The asymmetric stretch, which has \(B_1\) symmetry, may be excited in a Raman process in which one photon is \(x\)-polarized and the other \(z\)-polarized.

---

\(^7\)It is important not to confuse molecular orbitals (the energy levels that individual electrons may occupy within the molecule) with electronic states (arising from the different possible arrangements of all the molecular electrons amongst the molecular orbitals, e.g. the electronic states of \(NH_3\) are NOT the same thing as the molecular orbitals we derived earlier in the course. These orbitals were an incomplete set, based only on the valence \(s\) electrons in the molecule. Inclusion of the \(p\) electrons is required for a full treatment of the electronic states. The \(H_2O\) example above should hopefully clarify this point.

\(^8\)‘\(x\)-polarized’ means that the electric vector of the light (an electromagnetic wave) oscillates along the direction of the \(x\) axis.

\(^9\)You will cover Raman scattering (also known as Raman spectroscopy) in more detail in later courses. The aim here is really just to alert you to its existence and to show how it may be used to access otherwise inaccessible vibrational modes.