2.10: Derivando la Ley de Boyle de la Mecánica Newtoniana

Podemos derivar la ley de Boyle de la mecánica newtoniana. Esta derivación supone que las moléculas de gas se comportan como masas puntuales que no interactúan entre sí. La presión del gas resulta de colisiones de las moléculas de gas con las paredes del contenedor. La contribución de una colisión a la fuerza en la pared es igual al cambio en el impulso de la molécula dividido por el tiempo entre colisiones. La magnitud de esta fuerza depende de la velocidad de la molécula y del ángulo en el que golpea la pared. Cada colisión de este tipo contribuye a la presión que es igual a la fuerza dividida por el área de la pared. Para encontrar la presión de este modelo, es necesario promediar todas las velocidades moleculares posibles y todos los ángulos de colisión posibles. En el capítulo 4, derivamos de esta manera la ley de Boyle.

Podemos hacer una derivación simplificada haciendo una serie de suposiciones. Suponemos que todas las moléculas en una muestra de gas tienen la misma velocidad. Llamémoslo\(u\). Como se esboza en la Figura 3, suponemos que el contenedor es una caja cúbica cuya longitud de borde es\(d\). Si consideramos todas las colisiones entre moléculas y paredes, es claro que cada pared experimentará\({1}/{6}\) de las colisiones; o, cada par de paredes opuestas experimentará\({\mathrm{1}}/{\mathrm{3}}\) de las colisiones. En lugar de promediar todos los ángulos posibles en los que una molécula podría chocar contra una pared y todos los tiempos posibles entre colisiones, asumimos que las moléculas viajan a velocidad constante de ida y vuelta entre caras opuestas de la caja. Al ser masas puntuales, nunca chocan entre sí. Si suponemos que\({\mathrm{1}}/{\mathrm{3}}\) de las moléculas van y vienen entre cada par de paredes opuestas, podemos esperar lograr el mismo tipo de promedio en la configuración de nuestro modelo artificial que logramos promediando sobre la distribución real de ángulos y velocidades. De hecho, este resulta ser el caso; la derivación a continuación obtiene el mismo resultado que el tratamiento riguroso que desarrollamos en el Capítulo 4.

Figura 3. Modelo simplificado para velocidades de moléculas de gas en una caja cúbica.

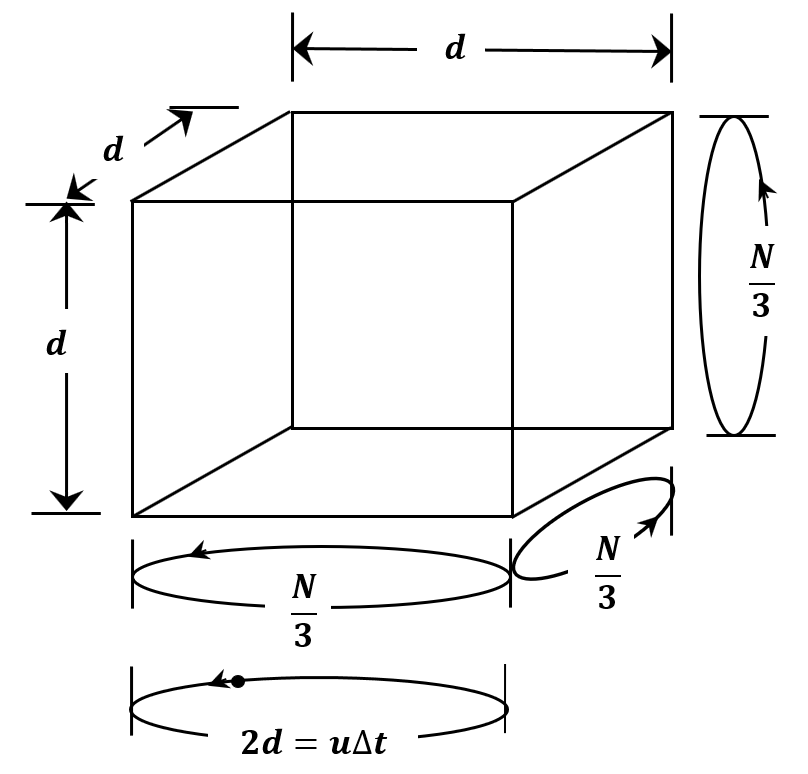
Dado que cada molécula va y viene entre paredes opuestas, choca con cada pared una vez durante cada viaje de ida y vuelta. En cada colisión, la velocidad de la molécula permanece constante, pero su dirección cambia 180\({}^{o}\); es decir, la velocidad de la molécula cambia de\(\mathop{u}\limits^{\rightharpoonup}\) a\(-\mathop{u}\limits^{\rightharpoonup}\). Dejando\(\Delta t\) ser el tiempo requerido para un viaje de ida y vuelta, la distancia recorrida en un viaje de ida y vuelta es

\[\begin{aligned} 2d & =\left|\mathop{u}\limits^{\rightharpoonup}\right|\Delta t \\ ~ & =u\Delta t \end{aligned}\]

La magnitud del cambio de momento para una molécula en una colisión es

\[\begin{align*} \left|\Delta (m\mathop{u}\limits^{\rightharpoonup})\right| &=\left|m{\mathop{u}\limits^{\rightharpoonup}}_{final}-m{\mathop{u}\limits^{\rightharpoonup}}_{initial}\right| \\[4pt] &=\left|m{\mathop{u}\limits^{\rightharpoonup}}_{final}-\left({-m\mathop{u}\limits^{\rightharpoonup}}_{final}\right)\right| \\[4pt] &=2mu \end{align*}\]

La magnitud de la fuerza en la pared de una colisión es

\[F=\frac{\left|\Delta \left(m\mathop{u}\limits^{\rightharpoonup}\right)\right|}{\Delta t}=\frac{2mu}{\left({2d}/{u}\right)}=\frac{mu^2}{d}\]

y la contribución de presión de una colisión en la pared, de área\(d^2\), es

\[P=\frac{F}{A}=\frac{mu^2}{d\bullet d^2}=\frac{{mu}^2}{d^3}=\frac{{mu}^2}{V}\]

para que tengamos

\[PV=mu^2\]

de la colisión de una molécula con una pared.

Si el número de moléculas en la caja es\(N\),\(N/3\) de ellas hacen colisiones con esta pared, de manera que la presión total en una pared atribuible a todas las\(N\) moléculas en la caja es

\[P=\frac{mu^2}{V}\frac{N}{3}\]

o

\[PV=\frac{Nmu^2}{3}\]

Ya que la ecuación de gas ideal se puede escribir como\(PV=NkT\) vemos\({Nmu^2}/{3}=NkT\) eso para que\(mu^2=3kT\) y

\[u=\sqrt{\frac{3kT}{m}}\]

Así, hemos encontrado una relación entre la velocidad molecular y la temperatura del gas. (La velocidad real de una molécula,\(v\), puede tener cualquier valor entre cero y, para propósitos actuales, infinito. Cuando promediamos los valores de\(v^2\) para muchas moléculas, encontramos el valor promedio de las velocidades al cuadrado,\(\overline{v^2}\). En el capítulo 4, nos encontramos con eso\(u^2=\overline{v^2}\). Es decir, la velocidad promedio que utilizamos en nuestra derivación resulta ser una cantidad llamada velocidad media cuadrática,\(v_{rms}=u=\sqrt{\overline{v^2}}\).) Este resultado también nos da la energía cinética (promedio) de una sola molécula de gas:

\[KE=\frac{mu^2}{2}=\frac{3kT}{2}\]

A partir de esta derivación, tenemos un modelo mecánico simple que explica la ley de Boyle como consecuencia lógica de moléculas punto-masa colisionando con las paredes de su contenedor. Al combinar este resultado con la ecuación de gas ideal, encontramos que la velocidad promedio de las moléculas de gas ideales depende únicamente de la temperatura. De esto tenemos el resultado muy importante de que la energía cinética traslacional de un gas ideal depende únicamente de la temperatura.

Dado que nuestras moléculas punto-masa que no interactúan no tienen energía potencial derivada de sus interacciones entre sí, su energía cinética traslacional es la totalidad de su energía. (Debido a que dos de esas moléculas no se atraen ni se repelen entre sí, no se requiere ningún trabajo para cambiar la distancia entre ellas. El trabajo asociado a cambiar el volumen de una muestra confinada de un gas ideal surge por la presión que las moléculas ejercen sobre las paredes del contenedor; la presión surge por la energía cinética de las moléculas). La energía de un mol de moléculas de gas ideales monatómicas es

\[KE=\left({3}/{2}\right)RT\]

Cuando ampliamos nuestro concepto de gases ideales para incluir moléculas que tienen energía rotacional o vibratoria, pero que no se atraen ni se repelen entre sí, sigue siendo cierto que la energía de una muestra macroscópica depende únicamente de la temperatura. Sin embargo, la energía molar de dicho gas es mayor que\(\left({3}/{2}\right)RT\), debido a la energía asociada a estos movimientos adicionales.

Hacemos uso extensivo de la conclusión de que la energía de un gas ideal depende únicamente de la temperatura. Resulta que esta conclusión se desprende rigurosamente de la segunda ley de la termodinámica. En el Capítulo 10, mostramos que

\[{\left(\frac{\partial E}{\partial V}\right)}_T={\left(\frac{\partial E}{\partial P}\right)}_T=0\]

para una sustancia que obedece a la ecuación de gas ideal; a temperatura constante, la energía de un gas ideal es independiente del volumen e independiente de la presión. En tanto que la presión, el volumen y la temperatura sean las únicas variables necesarias para especificar su estado, las leyes de la termodinámica implican que la energía de un gas ideal depende únicamente de la temperatura.

Si bien la energía de un gas ideal es independiente de la presión, la energía de un gas real es una función de la presión a una temperatura dada. A presiones y temperaturas ordinarias, esta dependencia es débil y a menudo se puede descuidar. La primera investigación experimental de este tema la realizó James Prescott Joule, para quien se nombra a la unidad de energía SI. A partir de 1838, Joule realizó una larga serie de medidas cuidadosas del equivalente mecánico del calor. Estas mediciones formaron la base experimental original para la teoría cinética del calor. Entre los primeros experimentos de Joule se encontró un intento de medir el calor absorbido por un gas a medida que se expandió en un contenedor evacuado, un proceso conocido como expansión libre. No se observó absorción de calor, lo que implicó que la energía del gas no se vio afectada por el cambio de volumen. Sin embargo, es difícil hacer este experimento con una precisión significativa.

Posteriormente, Joule colaboró con William Thomson (Lord Kelvin) en un enfoque experimental algo diferente para esencialmente la misma cuestión. El experimento de Joule-Thomson proporciona una medida mucho más sensible de los efectos de las fuerzas intermoleculares de atracción y repulsión sobre la energía de un gas durante su expansión. Dado que nuestra definición de un gas ideal incluye la estipulación de que no hay fuerzas intermoleculares, el experimento de Joule-Thomson es consistente con la conclusión de que la energía de un gas ideal depende únicamente de la temperatura. Sin embargo, dado que las fuerzas intermoleculares no son cero para ningún gas real, nuestro análisis llega a esta conclusión de una manera algo indirecta. La complicación surge porque los resultados de Joule-Thomson no son del todo consistentes con la idea de que todas las propiedades de un gas real se acercan a las de un gas ideal a una presión suficientemente baja. (El mejor de los modelos puede tener limitaciones.) Se discute el experimento de Joule-Thomson en la Sección 10.14.