2.11: La Fórmula Barométrica

Podemos medir la presión de la atmósfera en cualquier lugar mediante el uso de un barómetro. Un barómetro de mercurio es un tubo sellado que contiene una columna vertical de mercurio líquido. El espacio en el tubo por encima del mercurio líquido está ocupado por vapor de mercurio. Dado que la presión de vapor del mercurio líquido a temperaturas ordinarias es muy baja, la presión en la parte superior de la columna de mercurio es muy baja y generalmente puede ignorarse. La presión en la parte inferior de la columna de mercurio es igual a la presión de una columna de aire que se extiende desde la elevación del barómetro hasta la parte superior de la atmósfera terrestre. A medida que llevamos el barómetro a mayores altitudes, encontramos que la altura de la columna de mercurio disminuye, porque cada vez menos de la atmósfera está por encima del barómetro.

Figura 4. Presión atmosférica versus altitud.

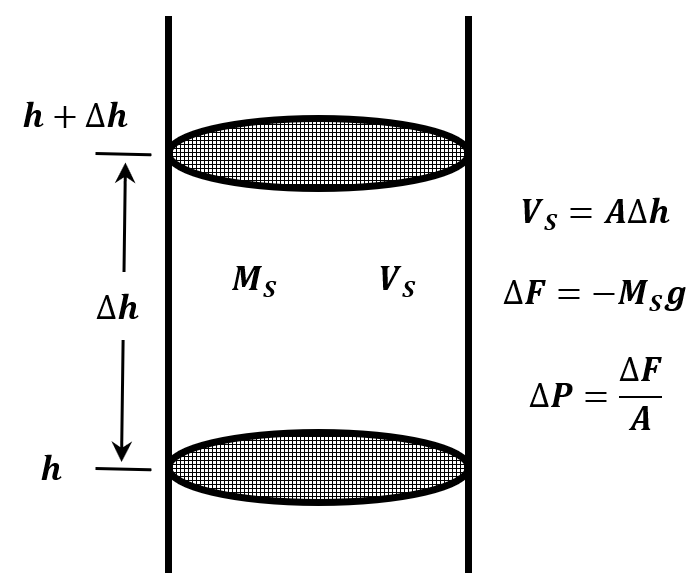
Si asumimos que la atmósfera está compuesta por un gas ideal y que su temperatura es constante, podemos derivar una ecuación para la presión atmosférica en función de la altitud. Imagine una columna cilíndrica de aire que se extiende desde la superficie terrestre hasta la parte superior de la atmósfera (Figura 4). La fuerza ejercida por esta columna en su base es el peso del aire en la columna; la presión es este peso dividido por el área transversal de la columna. Deje que el área de la sección transversal de la columna sea\(A\).

Considera una breve sección de esta columna. Que la parte inferior de esta sección esté a una\(h\) distancia de la superficie terrestre, mientras que su parte superior está a una\(h+\Delta h\) distancia de la superficie terrestre. El volumen de esta sección cilíndrica es entonces\(V_S=A\Delta h\). Que la masa del gas en esta sección sea\(M_S\). La presión a\(h+\Delta h\) es menor que la presión a\(h\) por el peso de este gas dividido por el área de la sección transversal. El peso del gas es\(M_Sg\). La diferencia de presión es\(\Delta P=-{M_Sg}/{A}\). Tenemos

\[\frac{P\left(h+\Delta h\right)-P\left(h\right)}{\Delta h}=\frac{\Delta P}{\Delta h}=\frac{-M_Sg}{A\Delta h}=\frac{-M_Sg}{V_S}\]

Ya que estamos asumiendo que la muestra de gas en la sección cilíndrica se comporta de manera ideal, tenemos\(V_S={n_SRT}/{P}\). Sustituyendo\(V_S\) y tomando el límite como\(\Delta h\to 0\), encontramos

\[\frac{dP}{dh}=\left(\frac{{-M}_Sg}{n_SRT}\right)P=\left(\frac{{-n}_S\overline{M}g}{n_SRT}\right)P=\left(\frac{-mg}{kT}\right)P\]

donde introducimos\(n_S\) como el número de moles de gas en la muestra,\(\overline{M}\) como la masa molar de este gas, y\(m\) como la masa de una molécula de atmósfera individual. La última igualdad a la derecha hace uso de las identidades\(\overline{M}=m\overline{N}\) y\(R=\overline{N}k\). Separando variables e integrando entre límites\(P\left(0\right)=P_0\) y\(P\left(h\right)=P\), encontramos

\[\int^P_{P_0}{\frac{dP}{P}}=\left(\frac{-mg}{kT}\right)\int^h_0{dh}\]

para que\[{ \ln \left(\frac{P}{P_0}\right)\ }=\frac{-mgh}{kT}\]

y

\[P=P_0\mathrm{exp}\left(\frac{-mgh}{kT}\right)\]

Cualquiera de estas últimas relaciones se denomina frecuentemente fórmula barométrica.

Si dejamos\(\eta\) ser el número de moléculas por unidad de volumen,\(\eta ={N}/{V}\), podemos escribir\(P={NkT}/{V}=\eta kT\) y\(P_0={\eta }_0kT\) para que la fórmula barométrica pueda expresarse en términos de estas densidades numéricas como

\[\eta ={\eta }_0\mathrm{exp}\left(\frac{-mgh}{kT}\right)\]