11.7: La fugacidad de un gas

Resulta que la dependencia de la presión de la energía libre de Gibbs es útil con más frecuencia que la de la entalpía o entropía. A partir de la relación definitoria\(G=H-TS\), y los resultados anteriores, encontramos

\[{\Delta }_fG^o_A\left({HIG}^o\right)={\Delta }_fH^o_A\left({HIG}^o\right)-T{\Delta }_fS^o_A\left({HIG}^o\right)\]\[={\overline{H}}_A\left(P\right)+\int^{P^*}_P{\left[\overline{V}-T{\left(\frac{\partial \overline{V}}{\partial T}\right)}_P\right]dP}\]\[-T{\overline{S}}_A\left(P\right)+\int^{P^*}_P{T{\left(\frac{\partial \overline{V}}{\partial T}\right)}_PdP}+\int^{P^o}_{P^*}{\frac{RT}{P}dP}\]\[={\overline{G}}_A\left(P\right)-\int^P_{P^*}{\overline{V}dP}-\int^{P^*}_{P^o}{\frac{RT}{P}dP}\]donde hemos invertido la dirección de integración en las integrales restantes. Nuevamente, no podemos evaluar las integrales con P* = 0. Para superar esta dificultad, introducimos un recurso inteligente: sumamos y restamos la misma integral, obteniendo

\[{\Delta }_fG^o_A\left({HIG}^o\right)={\overline{G}}_A\left(P\right)-\int^P_{P^*}{\overline{V}dP}-\int^{P^*}_{P^o}{\frac{RT}{P}dP}\]\[-\int^P_{P^*}{\frac{RT}{P}dP}+\int^P_{P^*}{\frac{RT}{P}dP}\]

\[ ={\overline{G}}_A\left(P\right)-\int^P_{P^*}{\left[\overline{V}-\frac{RT}{P}\right]dP}-\int^P_{P^o}{\frac{RT}{P}dP}\]

Este resultado es fundamental. Lo volveremos a derivar más tarde por un argumento ligeramente diferente. Por ahora, evaluamos la última integral y reorganizamos la ecuación a la forma en que la escribimos con más frecuencia:

\[{\overline{G}}_A\left(P\right)={\Delta }_fG^o_A\left({HIG}^o\right)+RT{ \ln \left(\frac{P}{P^0}\right)\ }+RT\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP}\]

Al hacerlo, utilizamos el hecho de que

\[\frac{\overline{V}}{RT}-\frac{1}{P}\]

se desvanece para cualquier gas cuando la presión es suficientemente baja, lo que significa que la integral de\(P^*\) a\(P\) permanece finita cuando dejamos\(P^*\to 0\).

Recapitulando: La última ecuación relaciona la energía libre de Gibbs de un mol de un gas real a presión\(P\) y temperatura\(T\)\({\overline{G}}_A\left(P\right)\),, a la energía libre de Gibbs de formación del gas en su estado estándar\({\Delta }_f\)\(G^o_A\left({HIG}^o\right)\),, donde el estado estándar es el hipotético gas ideal en \(P=P^o=1\ \mathrm{bar}\)y la misma temperatura. (Escribimos “\(RT{ \ln \left({P}/{P^o}\right)\ }\)” en lugar de “\(RT{ \ln P\ }\)” para enfatizar que el argumento del logaritmo es una cantidad adimensional.)

Si el gas es ideal, el integrando es cero a cualquier presión. Para un gas ideal, la energía libre de Gibbs, a presión\(P\) y temperatura\(T\), está relacionada con la energía libre de Gibbs en el estado estándar por

\[{\overline{G}}_A\left(P\right)=G^o_A\left(\mathrm{1\ bar}\right)+RT{ \ln \left(\frac{P}{P^o}\right)\ }\](gas ideal)

Esta observación nos permite dar una interpretación física a la integral

\[\int^P_0{\left[\overline{V}-\frac{RT}{P}\right]dP}=RT\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP}\]

Evidentemente, esta integral es la diferencia entre la energía libre de Gibbs de un mol del gas real y la energía libre de Gibbs que tendría si se comportara como un gas ideal. Cuando lo agregamos a la energía libre de Gibbs del hipotético gas ideal, obtenemos la energía libre de Gibbs del gas real.

Para un gas ideal, la energía libre de Gibbs es una función simple de su presión. Resulta útil ver la integral como una contribución a una “presión corregida”. La “corrección” es un ajuste a la presión que, en nuestros cálculos, hace que el gas real se comporte como un gas ideal. La idea es que podamos expresar la energía libre de Gibbs en función de esta presión corregida, a la que llamamos la fugacidad, y a la que le damos el símbolo “\(f\)”. Por lo tanto, la fugacidad es una función de la presión. Fugacidad también tiene las unidades de presión, que siempre tomamos como barras. Definimos la fugacidad de\(A\) a presión\(P\),\(f_A\left(P\right)\), por

\[{\overline{G}}_A\left(P\right)={\Delta }_fG^o_A\left({HIG}^o\right)+RT{ \ln \left(\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right)\ }\](gas real)

La fugacidad\(f_A\left({HIG}^o\right)\), y la energía libre de formación estándar de Gibbs\({\Delta }_fG^o_A\left({HIG}^o\right)\), describen el mismo estado. Definimos la fugacidad en este estado estándar como una barra. Es decir, la fugacidad de una sustancia en su hipotético estado estándar ideal-gas,\(f_A\left({HIG}^o\right)\), es una constante cuyo valor es de 1 bar. (Si queremos expresar fugacidad en unidades de, digamos, pascales, entonces)\(P^o=f_A\left({HIG}^o\right)={10}^5\ \mathrm{Pa}\).

Podemos calcular la fugacidad de un gas real, a presión\(P\) y temperatura\(T\), a partir de

\[RT{ \ln \left(\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right)\ }=\ RT{ \ln \left(\frac{P}{P_0}\right)\ }+RT\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP}\]

Nos resulta útil introducir una función de presión que llamamos el coeficiente de fugacidad,\({\gamma }_A\left(P\right)\). Lo definimos como

\[{\gamma }_A\left(P\right)=\frac{f_A\left(P\right)}{P}\]

Desde entonces\(f_A\left({HIG}^o\right)=P^o=1\ \mathrm{bar}\), tenemos

\[{ \ln {\gamma }_A\left(P\right)\ }=\int^P_0{\left[\frac{\overline{V}}{RT}-\frac{1}{P}\right]dP}\]

Figura 3. Descripción gráfica de\(\ln \gamma\)

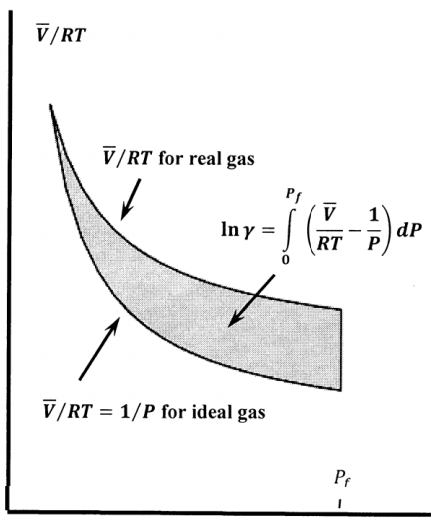
La Figura 3 muestra gráficamente estas cantidades. El área sombreada es\({ \ln {\gamma }_A\left(P\right)\ }\).