18.3: La ecuación de Schrödinger para una partícula en una caja

Un problema generalmente llamado la partícula en una caja proporciona una ilustración conveniente de los principios involucrados en la configuración y resolución de la ecuación de Schrödinger. Además de ser una buena ilustración, el problema también demuestra ser una aproximación útil a muchos sistemas físicos. El enunciado del problema es sencillo. Tenemos una partícula de masa\(m\) que está obligada a moverse solo en una dimensión. Para ubicaciones en el intervalo\(0\le x\le \ell\), la partícula tiene cero energía potencial. Para ubicaciones fuera de este rango, la partícula tiene energía potencial infinita. Dado que la partícula no puede tener energía infinita, esto significa que nunca podrá encontrar su camino hacia ubicaciones fuera del intervalo\(0\le x\le \ell\). Podemos pensar en esta partícula como una perla que se mueve sobre un alambre, con topes ubicados en el cable en\(x=0\) y en\(x=\ell\). También podemos pensarlo como confinado a una caja unidimensional de longitud\(\ell\), que es el punto de vista representado por el nombre. La partícula en un modelo de caja se esquematiza en la Figura 1.

Figura 1. Energía potencial versus distancia para una partícula en una caja.

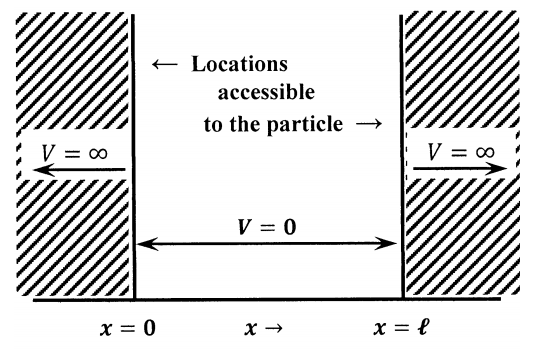
Las restricciones de energía potencial significan que la amplitud de la función de onda de la partícula debe ser cero,\(\psi \left(x\right)=0\), cuando el valor de\(x\) se encuentra en el intervalo

\[ - \infty x < 0\]

o

\[ \ell < x < + \infty\]

Suponemos que la probabilidad de encontrar la partícula no puede cambiar abruptamente cuando su ubicación cambia en una cantidad arbitrariamente pequeña. Esto quiere decir que la función de onda debe ser continua, y de ello se deduce que\(\psi \left(0\right)=0\) y\(\psi \left(\ell \right)=0\). Dentro de la caja, la ecuación de Schrödinger de la partícula es

\[-\left(\frac{h^2}{8{\pi }^2m}\right)\frac{d^2\psi }{dx^2}=E\psi\]

y buscamos aquellas funciones\(\psi \left(x\right)\) que satisfagan tanto esta ecuación diferencial como las ecuaciones de restricción\(\psi \left(0\right)=0\) y\(\psi \left(\ell \right)=0\). Resulta que hay infinitamente muchas soluciones de este tipo,\({\psi }_n\), cada una de las cuales corresponde a un nivel de energía único,\(E_n\).

Para encontrar estas soluciones, primero suponemos, guiados por nuestras consideraciones en el § 2, que las soluciones serán de la forma\[\psi \left(x\right)=A{\mathrm{sin} \left(ax\right)\ }+B{\mathrm{cos} \left(bx\right)\ }\]

Una solución debe satisfacer

\[\psi \left(0\right)=A{\mathrm{sin} \left(0\right)\ }+B{\mathrm{cos} \left(0\right)\ }=B{\mathrm{cos} \left(0\right)=0\ }\]

para que\(B=0\). En el otro extremo de la caja, debemos tener

\[\psi \left(\ell \right)=A{\mathrm{sin} \left(a\ell \right)\ }=0\]

lo que significa que\(a\ell =n\pi\), donde\(n\) está cualquier entero:\(n\ =1,\ 2,\ \dots .\) Por lo tanto, tenemos

\[a={n\pi }/{\ell }\]

y las únicas ecuaciones de la forma propuesta que satisfacen las condiciones en los extremos de la caja son

\[{\psi }_n\left(x\right)=A{\mathrm{sin} \left({n\pi x}/{\ell }\right)\ }\]

Para probar si estas ecuaciones satisfacen la ecuación de Schrödinger, verificamos

\[-\left(\frac{h^2}{8{\pi }^2m}\right)\frac{d^2}{dx^2}\left[A{\mathrm{sin} \left(\frac{n\pi x}{\ell }\right)\ }\right]=E_n{\psi }_n\]

y encuentra

\[\left(\frac{h^2}{8{\pi }^2m}\right){\left(\frac{n\pi }{\ell }\right)}^2\left[A{\mathrm{sin} \left(\frac{n\pi x}{\ell }\right)\ }\right]=\left(\frac{n^2h^2}{8{m\ell }^2}\right){\psi }_n=E_n{\psi }_n\]

para que las funciones de onda\({\psi }_n\left(x\right)=A{\mathrm{sin} \left({n\pi x}/{\ell }\right)\ }\) sean de hecho soluciones y la energía\(E_n\),, asociada con la función de onda\({\psi }_n\left(x\right)\) es

\[E_n=\frac{n^2h^2}{8{m\ell }^2}\]

Vemos que los valores de energía están cuantificados; aunque hay infinitamente muchos niveles de energía\(E_n\), solo números reales muy particulares —los dados por la ecuación anterior— corresponden a energías que la partícula puede tener. Si bosquejamos las primeras funciones de onda,\({\psi }_n\left(x\right)\), vemos que siempre hay\(n-1\) ubicaciones dentro de la caja en las que\({\psi }_n\left(x\right)\) es cero. Estas ubicaciones se llaman nodos. Una vez que conocemos\(n\), conocemos el número de nodos, y podemos bosquejar la forma general de la función de onda correspondiente. Las tres primeras funciones de onda y sus cuadrados se esbozan en la Figura 2.

Figura 2. Funciones de onda para una partícula en una caja.

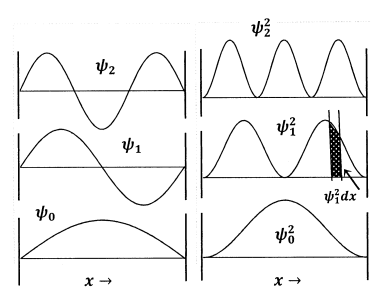
En este punto, hemos encontrado un conjunto completo de infinitamente muchas soluciones, a excepción del parámetro\(A\). Para determinar\(A\), interpretamos\({\psi }^2\left(x\right)\) como una función de densidad de probabilidad, y requerimos que la probabilidad de encontrar la partícula en la caja sea igual a la unidad. Esto significa que

\[1=\int^{\ell }_0{A^2{{\mathrm{sin}}^2 \left(\frac{n\pi x}{\ell }\right)\ }dx}=A^2\int^{\ell }_0{\left[\frac{1}{2}-\frac{1}{2}{\mathrm{cos} \left(\frac{2n\pi x}{\ell }\right)\ }\right]dx}=A^2\left(\frac{\ell }{2}\right)\]

de manera que\(A=\sqrt{2/\ell }\), y las últimas olaslas funcionamientos son

\[{\psi }_n\left(x\right)=\sqrt{\frac{2}{\ell }}{\mathrm{sin} \left(\frac{n\pi x}{\ell }\right)\ }\]