20.7: Conjunto de microestados de una población determinada
- Page ID
- 74355
Hasta el momento, solo hemos considerado las probabilidades asociadas a la asignación de moléculas distinguibles a los niveles de energía permitidos. En la Sección 20.2, se introduce la hipótesis de que todos los estados cuánticos\(g_i\) degenerados con energía\(\epsilon_i\) son igualmente probables, de manera que la probabilidad de que una molécula tenga energía\(\epsilon _i\) es\(P_i=P\left(\epsilon _i\right)=g_i\rho \left(\epsilon _i\right)\). Haciendo esta sustitución, la suma de probabilidad total se convierte en
\[\begin{align*} 1&=\left(P_1+P_2+\dots +P_i+\dots \right)^N \\[4pt] &=\sum_{\left\{N_i\right\}}{\frac{N!}{N_1!N_2!\dots N_i!\dots }}P^{N_1}_1P^{N_2}_2\dots P^{N_i}_i\dots \\[4pt] &=\sum_{\left\{N_i\right\}}{\frac{N!g^{N_1}_1g^{N_2}_2\dots g^{N_i}_i\dots }{N_1!N_2!\dots N_i!\dots }}{\rho \left(\epsilon _1\right)}^{N_1}{\rho \left(\epsilon _2\right)}^{N_2}\dots {\rho \left(\epsilon _i\right)}^{N_i}\dots . \\[4pt] &=\sum_{\left\{N_i\right\}}{N!} \prod^{\infty}_{i=1} \left(\frac{g^{N_i}_i}{N_i!}\right) \rho \left(\epsilon_i\right)^{N_i} \\[4pt] &=\sum_{\left\{N_i\right\}} W\prod^{\infty }_{i=1}\rho \left(\epsilon _i\right)^{N_i} \end{align*}\]
donde usamos la notación
\[a_1\times a_2\times \dots a_i\times \dots a_{\omega }\times =\prod^{\omega }_{i=1}{a_i}\]
para productos extendidos e introducir la función
\[\begin{align*} W &= W\left(N_i,g_i\right) \\[4pt] &=W\left(N_1,g_1,N_2,g_2,\dots ,N_i,g_i,\dots .\right) \\[4pt] &=N!\prod^{\infty }_{i=1}{\left(\frac{g^{N_i}_i}{N_i!}\right)} \\[4pt] &= C\left(N_1,N_2,\dots ,N_i,\dots \right)\prod^{\infty }_{i=1}{g^{N_i}_i} \end{align*}\]
Por razones que se aclaran más adelante, tradicionalmente\(W\) se llama la probabilidad termodinámica. Este nombre es algo desafortunado, porque\(W\) es claramente diferente de una probabilidad ordinaria.
En la Sección 20. 5, observamos que\(P^{N_1}_1P^{N_2}_2\dots P^{N_i}_i\) es la probabilidad de que\(N_i\) las moléculas ocupen cada uno de los niveles de energía\(\epsilon _i\) y ese\({N!}/{\left(N_1!N_2!\dots N_i!\dots \right)}\) es el número de combinaciones de moléculas distinguibles que surgen del conjunto poblacional\(\{N_1,N_2,\dots ,N_i,\dots \}\). Ahora observamos que el producto extendido
\[{\rho \left(\epsilon _1\right)}^{N_1}{\rho \left(\epsilon _2\right)}^{N_2}\dots {\rho \left(\epsilon _i\right)}^{N_i}\dots .\]
es la probabilidad de cualquier asignación de las moléculas distinguibles a estados cuánticos tales que\(N_i\) las moléculas se encuentran en estados cuánticos cuyas energías están\(\epsilon _i\). Dado que una molécula dada de energía\(\epsilon _i\) puede estar en cualquiera de los estados cuánticos\(g_i\) degenerados, la probabilidad de que esté en el nivel de energía\(\epsilon _i\) es\(g_i\) -veces mayor que la probabilidad de que esté en cualquiera de estos estados cuánticos.
Microestados
Llamamos microestado a una asignación particular de moléculas distinguibles a los estados cuánticos disponibles. Para cualquier conjunto poblacional, hay muchas combinaciones. Cuando los niveles de energía son degenerados, cada combinación da lugar a muchos microestados. El factor\({\rho \left(\epsilon _1\right)}^{N_1}{\rho \left(\epsilon _2\right)}^{N_2}\dots {\rho \left(\epsilon _i\right)}^{N_i}\dots .\) es la probabilidad de cualquier microestado del conjunto poblacional\(\{N_1,N_2,\dots ,N_i,\dots \}\). Evidentemente, la probabilidad termodinámica
\[W=N!\prod^{\infty }_{i=1}{\left(\frac{g^{N_i}_i}{N_i!}\right)} \label{micro}\]
es el número total de microestados de ese conjunto poblacional.
Para ver directamente que el número de microestados viene dictado por la Ecuación\ ref {micro}, consideremos el número de formas en que podemos asignar moléculas\(N\) distinguibles a los estados cuánticos cuando el conjunto poblacional es\(\{N_1,N_2,\dots ,N_i,\dots \}\) y el nivel de energía\(\epsilon _i\) es\(g_i\) -fold degenerado. Comenzamos asignando las\(N_1\) moléculas en nivel de energía\(\epsilon _1\). Podemos elegir la primera molécula de entre cualquiera de las moléculas\(N\) distinguibles y podemos optar por colocarla en cualquiera de los estados\(g_1\) cuánticos cuya energía es\(\epsilon _1\). El número de formas en que podemos tomar estas decisiones es\({Ng}_1\). Podemos elegir la segunda molécula de entre las moléculas distinguibles\(N-1\) restantes. En la estadística de Boltzmann, podemos colocar cualquier número de moléculas en cualquier estado cuántico, por lo que nuevamente hay estados\(g_1\) cuánticos en los que podemos colocar la segunda molécula. El número total de formas en que podemos colocar la segunda molécula es\(\left(N-1\right)g_1\).
Por lo tanto, el número de formas en que se pueden elegir y colocar las moléculas primera y segunda es\(N\left(N-1\right)g^2_1\). Encontramos el número de formas en que las moléculas sucesivas pueden ser colocadas en los estados cuánticos de la energía\(\epsilon _1\) por el mismo argumento. La última molécula cuya energía es\(\epsilon _1\) puede elegirse de entre las moléculas\(\left(N-N_1+1\right)\) restantes y colocarse en cualquiera de los estados\(g_1\) cuánticos. El número total de formas de colocar las\(N_1\) moléculas en nivel de energía\(\epsilon _1\) es\(N\left(N-1\right)\left(N-2\right)\dots \left(N-N_1+1\right)g^{N_1}_1\).
Este total incluye todos los pedidos posibles para colocar cada conjunto de moléculas\(N_1\) distinguibles en cada conjunto posible de estados cuánticos. No obstante, el orden no importa; lo único que afecta al estado del sistema es qué moléculas entran en qué estado cuántico. (Cuando consideramos todas las formas en que nuestro procedimiento pone todas las moléculas en cualquiera de los estados cuánticos, encontramos que cualquier asignación de moléculas\(A\)\(B\), y\(C\) a cualquier conjunto particular de estados cuánticos ocurre seis veces. Selecciones en los órdenes\(A\)\(B\),\(C\)\(A\),\(C\),,\(B\)\(B\),\(A\),\(C\)\(B\),,\(C\),\(A\)\(C\),\(A\),\(B\) y\(C\),\(B\),\(A\) todas ponen las mismas moléculas en el mismo quantum estados.) Hay\(N_1!\) órdenes en las que nuestro procedimiento elige las\(N_1\) moléculas; para corregirlo, debemos dividirlas por\(N_1!\), de manera que el número total de asignaciones que queremos incluir en nuestro conteo sea
\[N\left(N-1\right)\left(N-2\right)\dots \left(N-N_1+1\right)g^{N_1}_1/N_1!\]
La primera molécula que asignamos al segundo nivel de energía puede elegirse de entre las moléculas\(N-N_1\) restantes y colocarse en cualquiera de los estados\(g_2\) cuánticos cuya energía es\(\epsilon _2\). La última se puede elegir entre las\(\left(N-N_1-N_2+1\right)\) moléculas restantes. El número de asignaciones de las\(N_2\) moléculas a\(g_2\) -fold degeneran estados cuánticos cuya energía es\(\epsilon _2\) es
\[\left(N-N_1\right)\left(N-N_1-1\right)\dots \left(N-N_1-N_2+1\right)g^{N_2}_2/N_2!\]
Cuando consideramos el número de asignaciones de moléculas a estados cuánticos con energías\(\epsilon _1\) y\(\epsilon _2\) tenemos
\[N\left(N-1\right)\dots \left(N-N_1+1\right)\left(N-N_1\right)\left(N-N_1-1\right)\dots\]\[\times \left(N-N_1-N_2+1\right)\left(\frac{g^{N_1}_1}{N_1!}\right)\left(\frac{g^{N_2}_2}{N_2!}\right)\]
Que sea el último nivel de energía para contener cualquier molécula\(\epsilon _{\omega }\). El número de formas en que las\(N_{\omega }\) moléculas pueden ser asignadas a los estados cuánticos con energía\(\epsilon _{\omega }\) es\(N_{\omega }\left(N_{\omega }-1\right)\dots \left(1\right)g^{N_{\omega }}_{\omega }/N_{\omega }!\) El número total de microestados para el conjunto poblacional\(\{N_1,N_2,\dots ,N_i,\dots \}\) se convierte
\[N\left(N-1\right)\dots \left(N-N_1\right)\left(N-N_1-1\right)\dots\]\[\times \left(N_{\omega }\right)\left(N_{\omega }-1\right)\dots \left(1\right)\prod^{\infty }_{i=1}{\left(\frac{g^{N_i}_i}{N_i!}\right)}=N!\prod^{\infty }_{i=1}{\left(\frac{g^{N_i}_i}{N_i!}\right)}\]
Cuando consideramos las estadísticas de Fermi-Dirac y Bose-Einstein, ya no es cierto que las moléculas sean distinguibles. Para las estadísticas de Fermi-Dirac, no se puede asignar más de una molécula a un estado cuántico particular. Para un conjunto de población determinado, las estadísticas de Boltzmann, Fermi-Dirac y Bose-Einstein producen diferentes números de microestados.
Es útil tener notación que nos permita especificar diferentes combinaciones y diferentes microestados. Si\(\epsilon _i\) es la energía asociada a la ecuación de onda la que describe una molécula en particular, es conveniente decir que la molécula está en nivel de energía\(\epsilon _i\); es decir, su estado cuántico es uno de los que tiene energía\(\epsilon _i\). Usando letras mayúsculas para representar moléculas, indicamos que la molécula\(A\) está en nivel de energía\(\epsilon _i\) por escrito\(\epsilon _i\left(A\right)\). Para indicar que\(A\),\(B\), y\(C\) están en\(\epsilon _i\), escribimos\(\epsilon _i\left(A,B,C\right)\). De igual manera, para indicar que las moléculas\(D\) y\(E\) están en\(\epsilon _k\), escribimos\(\epsilon _k\left(D,E\right)\). Para este sistema de cinco moléculas, la asignación\(\epsilon _i\left(A,B,C\right)\epsilon _k\left(D,E\right)\) representa una de las posibles combinaciones. El orden en que presentamos las moléculas que tienen una energía dada es inmaterial:\(\epsilon _i\left(A,B,C\right)\epsilon _k\left(D,E\right)\) y\(\epsilon _i\left(C,B,A\right)\epsilon _k\left(E,D\right)\) representan la misma combinación. Cuando una molécula cualquiera es distinguible de otras de la misma sustancia, las asignaciones en las que una molécula dada tiene diferentes energías son físicamente diferentes y representan diferentes combinaciones. Las asignaciones\(\epsilon _i\left(A,B,C\right)\epsilon _k\left(D,E\right)\) y\(\epsilon _i\left(D,B,C\right)\epsilon _k\left(A,E\right)\) representan diferentes combinaciones. En la Figura 2, representamos estas asignaciones de manera más esquemática.
Dos asignaciones cualesquiera en las que una molécula en particular ocupa diferentes estados cuánticos dan lugar a diferentes microestados. Si el nivel de\(i^{th}\) energía es triple degenerado, una molécula en cualquiera de los estados cuánticos\({\psi }_{i,1}\)\({\psi }_{i,2}\), o\({\psi }_{i,3}\) tiene energía\(\epsilon _i\). Escribamos
\[{\psi }_{i,1}\left(A,B\right){\psi }_{i,2}\left(C\right){\psi }_{k,1}\left(DE\right)\]
para indicar el microestado que surge de la combinación\(\epsilon _i\left(A,B,C\right)\epsilon _k\left(D,E\right)\) en la que las moléculas\(A\) y\(B\) ocupan\({\psi }_{i,1}\), la molécula\(C\) ocupa\({\psi }_{i,2}\), y las moléculas\(D\) y\(E\) ocupan\({\psi }_{k,1}\). Entonces,
\[{\psi }_{i,1}\left(A,B\right){\psi }_{i,2}\left(C\right){\psi }_{k,1}\left(DE\right)\]\[{\psi }_{i,1}\left(B,C\right){\psi }_{i,2}\left(A\right){\psi }_{k,1}\left(DE\right)\]\[{\psi }_{i,1}\left(A\right){\psi }_{i,2}\left(B,C\right){\psi }_{k,1}\left(DE\right)\]
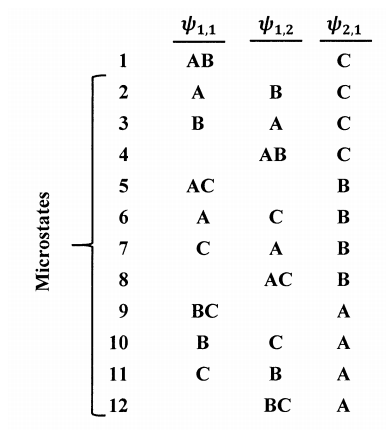
son tres de los muchos microestados que surgen de la combinación\(\epsilon _i\left(A,B,C\right)\epsilon _k\left(D,E\right)\). La Figura 3 muestra todos los microestados posibles para el conjunto poblacional\(\{2,1\}\) cuando los estados cuánticos de una molécula son\({\psi }_{1,1}\),\({\psi }_{1,2}\), y\({\psi }_{2,1}\).