21.2: Método Lagrange de multiplicadores indeterminados

El método de Lagrange de multiplicadores indeterminados es un método para encontrar el valor mínimo o máximo de una función sujeta a una o más restricciones. Un ejemplo sencillo sirve para aclarar el problema general. Considera la función

\[z=z_0\ \mathrm{exp}\left(x^2+y^2\right)\nonumber \]

donde\(z_0\) es una constante. Esta función es una superficie de revolución, que es tangente al plano\(z=z_0\) en\(\left(0,0,z_0\right)\). El punto de tangencia es el valor mínimo de\(z\). En cualquier otro punto del\(xy\) -plano,\(z\left(x,y\right)\) es mayor que\(z_0\). Si cualquiera\(x\) o\(y\) se vuelve arbitrariamente grande, también\(z\) lo hace. Si proyectamos un contorno de constante\(z\) sobre el\(xy\) plano, la proyección es un círculo de radio

\[r=\left(x^2+y^2\right)^{1/2}.\]

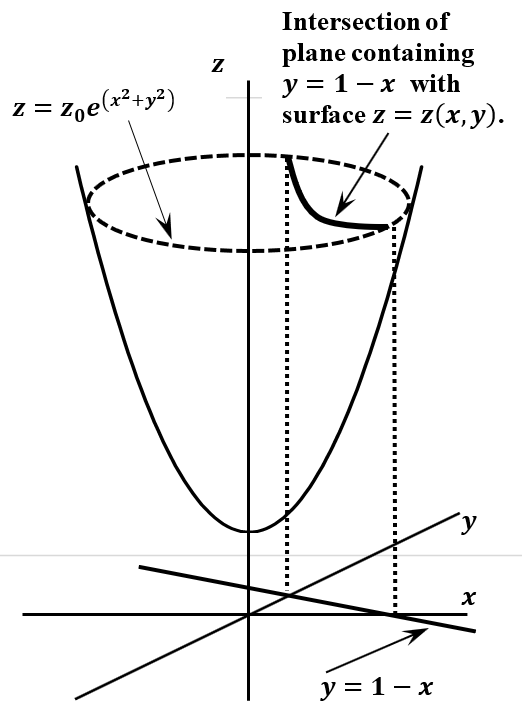
Supongamos que introducimos una condición adicional; requerimos\(y=1-x\). Entonces pedimos el valor más pequeño de\(z\) congruente con esta restricción. En el\(xy\) plano -la restricción es una línea de pendiente\(-1\) e intercepción\(1\). Un plano que incluye esta línea y es paralelo al\(z\) eje -interseca la función\(z\). Como se esboza en la Figura 1, esta intersección es una curva. Lejos del origen, el valor\(z\) en el que se produce la intersección es grande. Más cerca del origen, el valor de\(z\) es menor, y hay algunos\(\left(x,y\right)\) en los que es mínimo. Nuestro objetivo es encontrar este mínimo.

Figura 1: Una superficie y una ecuación de restricción.

Hay una solución directa de este problema; podemos sustituir la ecuación de restricción\(y\) en la ecuación para\(\ z\), haciendo\(z\) una función de una sola variable,\(x\). Tenemos

\[ \begin{align*} z&=z_0\ \mathrm{exp} \left(x^2+{\left(1-x\right)}^2\right) \\[4pt] &=z_0\ \mathrm{exp} \left(2x^2-2x+1\right)\end{align*} \]

Para encontrar el mínimo, equiparamos la derivada a cero, dando

\[0=\frac{dz}{dx}=\left(4x-2\right)z_0\ \mathrm{exp} \left(2x^2-2x+1\right)\nonumber \]

para que el mínimo ocurra en\(x={1}/{2}\), y\(={1}/{2}\), y

\[z=z_0\ \mathrm{exp}\left({1}/{2}\right)\nonumber \]

Resolver tales problemas mediante la eliminación de variables puede llegar a ser difícil. El método de Lagrange de multiplicadores indeterminados es un método general, que suele ser fácil de aplicar y que se extiende fácilmente a casos en los que existen múltiples restricciones. Podemos ver cómo surge el método de Lagrange pensando más en nuestro ejemplo particular. Podemos imaginar que “caminamos” a lo largo de la línea de restricción en el\(xy\) plano y medimos el\(z\) que está directamente sobre la cabeza a medida que avanzamos. El problema es encontrar el valor mínimo del\(z\) que encontramos a medida que avanzamos por la línea. Esta perspectiva resalta la característica central del problema: Si bien es formalmente un problema en tres dimensiones (\(x\),\(y\), y\(z\)), la introducción de la restricción lo convierte en un problema bidimensional. Podemos pensar en una dimensión como un desplazamiento a lo largo de la línea\(y=1-x\), desde algún punto de partida arbitrario en la línea. La otra dimensión es la distancia perpendicular desde el\(xy\) plano -plano a la intersección con la superficie\(z\).

La parte relevante del\(xy\) plano es solo la línea de restricción unidimensional. Podemos reconocer esto parametrizando la línea. Vamos a\(t\) medir la ubicación en la línea relativa a algún punto inicial en el que\(t\ =\ 0\). Entonces tenemos\(x=x\left(t\right)\) y\(y=y\left(t\right)\) y

\[z\left(x,y\right)=z\left(x\left(t\right),y\left(t\right)\right)=z\left(t\right).\nonumber \]

El punto que buscamos es aquel en el que\({dz}/{dt}=0\).

Ahora examinemos un problema algo más general. Queremos una forma general de encontrar los valores\(\left(x,y\right)\) que minimizan (o maximizan) una función\(h=h\left(x,y\right)\) sujeta a una restricción de la forma\(c=g\left(x,y\right)\), donde\(c\) es una constante. Como en nuestro ejemplo, esta restricción requiere de una solución en la que\(\left(x,y\right)\) se encuentran en una línea particular. Si parametrizamos este problema, tenemos

\[h=h\left(x,y\right)=h\left(x\left(t\right),y\left(t\right)\right)=h\left(t\right)\nonumber \]

y

\[c=g\left(x,y\right)=g\left(x\left(t\right),y\left(t\right)\right)=g\left(t\right)\nonumber \]

Porque\(c\) es una constante,\({dc}/{dt}={dg}/{dt}=0\). La solución que buscamos es el punto en el que\(h\) es un extremo. En este punto,\({dh}/{dt}=0\). Por lo tanto, en el punto que buscamos, tenemos

\[\frac{dh}{dt}={\left(\frac{\partial h}{\partial x}\right)}_y\frac{dx}{dt}+{\left(\frac{\partial h}{\partial y}\right)}_x\frac{dy}{dt}=0\nonumber \]y\[\frac{dg}{dt}={\left(\frac{\partial g}{\partial x}\right)}_y\frac{dx}{dt}+{\left(\frac{\partial g}{\partial y}\right)}_x\frac{dy}{dt}=0\nonumber \]

Podemos multiplicar cualquiera de estas ecuaciones por cualquier factor, y el producto será cero. Multiplicamos\({dg}/{dt}\) por\(\lambda\) (dónde\(\lambda \neq 0\)) y restamos el resultado de\({dh}/{dt}\). Entonces, en el punto que buscamos,

\[0=\frac{dh}{dt}-\lambda \frac{dg}{dt}={\left(\frac{\partial h}{\partial x}-\lambda \frac{\partial g}{\partial x}\right)}_y\frac{dx}{dt}+{\left(\frac{\partial h}{\partial y}-\lambda \frac{\partial g}{\partial y}\right)}_x\frac{dy}{dt}\nonumber \]

Ya que podemos elegir\(x\left(t\right)\) y de\(y\left(t\right)\) cualquier manera que nos plazca, podemos asegurar eso\({dx}/{dt}\neq 0\) y\({dy}/{dt}\neq 0\) en el punto de solución. Si lo hacemos, los términos entre paréntesis deben ser cero en el punto de solución.

Por el contrario, establecer

\[{\left(\frac{\partial h}{\partial x}-\lambda \frac{\partial g}{\partial x}\right)}_y=0\nonumber \]y\[{\left(\frac{\partial h}{\partial y}-\lambda \frac{\partial g}{\partial y}\right)}_x=0\nonumber \]

es suficiente para asegurar que

\[\frac{dh}{dt}=\lambda \frac{dg}{dt}\nonumber \]

Ya que\({dg}/{dt}=0\), estas condiciones aseguran eso\({dh}/{dt}=0\). Esto significa que, si podemos encontrar un conjunto\(\{x,y,\lambda \}\) satisfactorio

\[{\left(\frac{\partial h}{\partial x}-\lambda \frac{\partial g}{\partial x}\right)}_y=0\nonumber \]y\[{\left(\frac{\partial h}{\partial y}-\lambda \frac{\partial g}{\partial y}\right)}_x=0\nonumber \] y\[c-g\left(x,y\right)=0\nonumber \]

entonces los valores de\(x\) y\(y\) deben ser los que hacen\(h\left(x,y\right)\) un extremo, sujeto a la restricción que\(c=g\left(x,y\right)\). No hemos demostrado que el conjunto\(\{x,y,\lambda \}\) existe, pero hemos demostrado que si existe, es la solución deseada.

Un mnemotécnico útil simplifica la tarea de generar la familia de ecuaciones que necesitamos para usar el método de Lagrange. El mnemotécnico nos llama a formar una nueva función, que es una suma de la función cuyo extremo buscamos y una serie de términos adicionales. Hay un término adicional para cada ecuación de restricción. Generamos este término poniendo la ecuación de restricción en la forma\(c-g\left(x,y\right)=0\) y multiplicando por un parámetro indeterminado. Para el caso que acabamos de considerar, la función mnemotécnica es

\[F_{mn}=h\left(x,y\right)+\lambda \left(c-g\left(x,y\right)\right)\nonumber \]

Podemos generar el conjunto de ecuaciones que describen el conjunto de soluciones\(\{x,y,\lambda \}\),, igualando las derivadas parciales de\(F_{mn}\) con respecto a\(x\)\(y\), y\(\lambda\) a cero. Es decir, el conjunto de soluciones satisface las ecuaciones simultáneas

\[\frac{\partial F_{mn}}{\partial x}=0\nonumber \]

\[\frac{\partial F_{mn}}{\partial y}=0\nonumber \]y\[\frac{\partial F_{mn}}{\partial \lambda }=0\nonumber \]

Si hay múltiples ecuaciones de restricción,\(c_{\lambda }-g_{\lambda }\left(x,y\right)=0\)\(c_{\alpha }-g_{\alpha }\left(x,y\right)=0\), y\(c_{\beta }-g_{\beta }\left(x,y\right)=0\), entonces la función mnemotécnica es

\[F_{mn}=h\left(x,y\right)+\lambda \left(c_{\lambda }-g_{\lambda }\left(x,y\right)\right)+\alpha \left(c_{\alpha }-g_{\alpha }\left(x,y\right)\right)+\beta \left(c_{\beta }-g_{\beta }\left(x,y\right)\right)\nonumber \]

y las ecuaciones simultáneas que representan el extremo restringido son

• \({\partial F_{mn}}/{\partial }x=0\),
• \({\partial F_{mn}}/{\partial }y=0\),
• \({\partial F_{mn}}/{\partial }\lambda =0\),
• \({\partial F_{mn}}/{\partial }\alpha =0\), y
• \({\partial F_{mn}}/{\partial }\beta =0\).

Para ilustrar el uso del mnemotécnico, volvamos al ejemplo con el que comenzamos. La ecuación mnemotécnica es

\[F_{mn}=z_0\ \mathrm{exp} \left(x^2+y^2\right)+\lambda \left(1-x-y\right)\nonumber \]

para que

\[\frac{\partial F_{mn}}{\partial x}=2xz_0\ \mathrm{exp} \left(x^2+y^2\right)-\lambda =0, \nonumber\]

\[\frac{\partial F_{mn}}{\partial y}=2yz_0\ \mathrm{exp} \left(x^2+y^2\right)-\lambda =0\nonumber \]

y

\[\frac{\partial F_{mn}}{\partial \lambda }=1-x-y=0 \nonumber\]

que rinden\(x={1}/{2}\), y\(={1}/{2}\), y\(\lambda =z_0\ \mathrm{exp} \left({1}/{2}\right)\).