21.7: El Modelo Microscópico para Cambio Reversible

Ahora volvamos al sistema cerrado (constante\(N\)) para desarrollar otra perspectiva sobre la dependencia de sus propiedades termodinámicas macroscópicas de los niveles de energía molecular y sus probabilidades. Nos comprometemos a describir el sistema utilizando el volumen y la temperatura como variables independientes. Al pensar en las probabilidades de nivel de energía, estipulamos que cualquier parámetro que afecte el estado del sistema permanezca constante. Específicamente, queremos decir que cualquier parámetro que aparezca en la ecuación de Schrödinger permanece constante. Por ejemplo, los niveles de energía de una partícula en una caja dependen de la masa de la partícula y la longitud de la caja. Cualquier parámetro de este tipo se llama una variable exógena. Si cambiamos una variable exógena (digamos la longitud de la caja) por una pequeña cantidad, todos los niveles de energía cambian en una pequeña cantidad, y todas las probabilidades cambian en una pequeña cantidad. Los niveles de energía y sus probabilidades son funciones suaves de la variable exógena. Si\(\xi\) es la variable exógena, tenemos

\[P_i=P\left(\epsilon_i\right)=g_i\rho \left(\epsilon_i\left(\xi \right)\right)\]

Un cambio en la variable exógena corresponde a un proceso macroscópico reversible.

Para una partícula en una caja, las sucesivas\({\psi }_i\) son funciones que dependen del número cuántico,\(i\), y la longitud de la caja,\(\ell\). Cuando cambiamos la longitud de la caja, la función de onda y su energía asociada cambian ambas. Ambas son funciones continuas de la longitud de la caja. La energía es

\[\epsilon_i=\frac{i^2h^2}{8m{\ell }^2}\]

Cambiar la longitud de la caja es análogo a cambiar el volumen de un sistema. Un cambio de volumen reversible implica trabajo. Vemos que cambiar la longitud de la caja sí funciona en la partícula en una caja, así como cambiar el volumen de un sistema tridimensional sí funciona en el sistema.

La temperatura juega un papel central en la descripción del equilibrio desde la perspectiva macroscópica. Podemos ver que la temperatura entra en la descripción del equilibrio desde la perspectiva microscópica a través de su efecto sobre los factores de probabilidad. Cuando aumentamos la temperatura de un sistema, su energía aumenta. La energía promedio de sus moléculas aumenta. La probabilidad de un nivel de energía debe depender de la temperatura. Evidentemente, las probabilidades de niveles de energía que son superiores a la energía promedio original aumentan cuando aumenta la temperatura. Las probabilidades de niveles de energía que son inferiores a la energía promedio original disminuyen cuando aumenta la temperatura. Los efectos del calor y el trabajo sobre los niveles de energía y sus poblaciones de equilibrio se esquematizan en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Los efectos del calor y el trabajo sobre los niveles de energía y sus poblaciones.

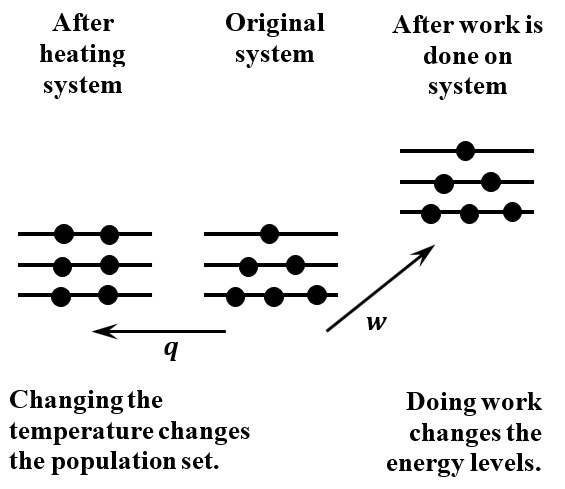
Para que nuestra teoría sea útil, la energía que medimos para un sistema macroscópico debe ser indistinguiblemente cercana al valor esperado de la energía del sistema calculada a partir de nuestro modelo microscópico:

\[E_{\mathrm{experiment}}\approx \left\langle E\right\rangle =N\left\langle \epsilon \right\rangle =N\sum^{\infty }_{i=1}{P_i\epsilon_i}\]

Podemos usar esta ecuación para relacionar las probabilidades\(P_i\),, con otras funciones termodinámicas. Dejando de lado la distinción entre las energías experimentales y esperadas, y asumiendo que las\(\epsilon_i\) y las\(P_i\) son variables continuas, encontramos el diferencial total

\[dE=N\sum^{\infty }_{i=1}{\epsilon_idP_i}+N\sum^{\infty }_{i=1}{{P_id\epsilon }_i}\]

Esta ecuación es importante porque describe un proceso macroscópico reversible en términos de las variables microscópicas\(\epsilon_i\) y\(P_i\).

Consideremos el primer término. Ya que\(N\) es una constante, tenemos de\(N^{\textrm{⦁}}_i=P_iN\) eso\(dN^{\textrm{⦁}}_i=NdP_i\). Sustituyendo, tenemos

\[\left(dE\right)_{\epsilon_i}=N\sum^{\infty }_{i=1}{\epsilon_idP_i}=\sum^{\infty }_{i=1}{\epsilon_i}dN^{\textrm{⦁}}_i\]

Esto afirma que la energía del sistema cambia si redistribuimos las moléculas entre los diversos niveles de energía. Si la redistribución saca moléculas de niveles de energía más bajos y las pone en niveles de energía más altos, la energía del sistema aumenta. Este es nuestro cuadro estadístico-mecánico del cambio en la posición de equilibrio que se produce cuando calentamos un sistema de moléculas independientes; la asignación de moléculas entre los niveles de energía disponibles se desplaza para poner más moléculas en niveles de energía más altos y menos en los inferiores. Esto corresponde a un incremento en la temperatura del sistema macroscópico.

En cuanto al sistema macroscópico, el primer término representa un incremento de calor agregado al sistema en un proceso reversible; es decir,

\[dq^{rev}=N\sum^{\infty }_{i=1}{\epsilon_idP_i}\]

El segundo término,\(N\sum^{\infty }_{i=1}{{P_id\epsilon }_i}\), es una contribución al cambio en la energía del sistema a partir de cambios reversibles en la energía de los diversos estados cuánticos, mientras que el número de moléculas en cada estado cuántico permanece constante. Este término corresponde a un proceso en el que los estados cuánticos (y sus energías) evolucionan de manera continua a medida que cambia el estado del sistema. El segundo término representa un incremento del trabajo realizado sobre el sistema en un proceso reversible; es decir

\[dw^{rev}=N\sum^{\infty }_{i=1}{{P_id\epsilon }_i}\]

Evidentemente, la expresión diferencial total para\(dE\) es la ecuación fundamental de la termodinámica expresada en términos de las variables que utilizamos para caracterizar el sistema molecular. Nos permite relacionar las variables que caracterizan nuestro modelo microscópico del sistema molecular con las variables que caracterizan al sistema macroscópico.

Para un sistema en el que el trabajo reversible es trabajo de presión-volumen, los niveles de energía dependen del volumen. A temperatura constante tenemos

\[dw^{rev}=-PdV=N\sum^{\infty }_{i=1}{{P_id\epsilon }_i}=N\sum^{\infty }_{i=1}{P_i{\left(\frac{\partial \epsilon_i}{\partial V}\right)}_TdV}\]

de manera que la presión del sistema\(P\),, está relacionada con las probabilidades de nivel de energía,\(P_i\), como

\[P=-N\sum^{\infty }_{i=1}{P_i{\left(\frac{\partial \epsilon_i}{\partial V}\right)}_T}\]

Para evaluar la presión, debemos saber cómo los niveles de energía dependen del volumen del sistema.

El primer término relaciona la entropía con las probabilidades de nivel de energía. Desde entonces\(dq^{rev}=TdS=N\sum^{\infty }_{i=1}{\epsilon_idP_i}\), tenemos\[dS=\frac{N}{T}\sum^{\infty }_{i=1}{\epsilon_idP_i}\]

Desde la función de distribución de Boltzmann tenemos

\(P_i=z^{-1}g_i\mathrm{exp}\left({-\epsilon_i}/{kT}\right)\), o

\[\epsilon_i=-kT\ln P_i +kT\ln g_i -kT\ln z \]

Sustituyendo en nuestra expresión por\(dS\), encontramos

\[dS=-Nk\sum^{\infty }_{i=1}{\left(\ln P_i \right)}dP_i+Nk\sum^{\infty }_{i=1}{\left(\ln g_i \right)}dP_i-Nk\left(\ln z \right)\sum^{\infty }_{i=1}{dP_i}\]

Ya que\(\sum^{\infty }_{i=1}{P_i}=1\), tenemos\(\sum^{\infty }_{i=1}{dP_i}=0\), y el último término se desvanece. Además,

\[\sum^{\infty }_{i=1}{d\left(P_i\ln P_i \right)}=\sum^{\infty }_{i=1}{\left(\ln P_i \right){dP}_i}+\sum^{\infty }_{i=1}{dP_i}=\sum^{\infty }_{i=1}{\left(\ln P_i \right){dP}_i}\]

para que

\[dS=-Nk\sum^{\infty }_{i=1}{d\left(P_i\ln P_i \right)}+Nk\sum^{\infty }_{i=1}{\left(\ln g_i \right)}dP_i\]

A cualquier temperatura, la relación de probabilidad para dos niveles de energía sucesivos cualesquiera es

\[\frac{P_{i+1}\left(T\right)}{P_i\left(T\right)}=\frac{P_{i+1}}{P_i}=\frac{g_{i+1}}{g_i}\mathrm{exp}\left(\frac{-\left(\epsilon_{i+1}-\epsilon_i\right)}{kT}\right)\]

En el límite a medida que la temperatura va a cero,

\[\frac{P_{i+1}}{P_i}\to 0\]

De ello se deduce que\(P_1\left(0\right)=1\) y\(P_i\left(0\right)=0\) para\(i>1\). Integrando de\(T=0\) a\(T\), la entropía del sistema va de\(S\left(0\right)=S_0\) a\(S\left(T\right)\), y las probabilidades de nivel de energía van de\(P_i\left(0\right)\) a\(P_i\left(T\right)\). Tenemos

\[\int^{S\left(T\right)}_{S_0}{dS}=-Nk\sum^{\infty }_{i=1}{\int^{P_i\left(T\right)}_{P_i\left(0\right)}{d\left(P_i\ln P_i \right)}}+Nk\sum^{\infty }_{i=1}{\int^{P_i\left(T\right)}_{P_i\left(0\right)}{\left(\ln g_i \right)dP_i}}\]

para que

\[S\left(T\right)-S_0=-Nk\sum^{\infty }_{i=1}{P_i\left(T\right)}\ln P_i\left(T\right) +NkP_1\left(0\right)\ln P_1\left(0\right) +Nk\sum^{\infty }_{i=1}{\left(\ln g_i \right)P_i\left(T\right)}-Nk\left(\ln g_1 \right)P_1\left(0\right)\]

Ya que\(P_1\left(0\right)=1\), se\(\ln P_1\left(0\right) \) desvanece. El cambio de entropía se convierte

\[S\left(T\right)-S_0=-Nk\sum^{\infty }_{i=1}{P_i}\left[\ln P_i -\ln g_i \right]-Nk\ln g_1 =-Nk\sum^{\infty }_{i=1}{P_i}\ln \rho \left(\epsilon_i\right) -Nk\ln g_1 \]

Nosotros tenemos\(S_0=Nk\ln g_1 \). Si\(g_1=1\), el nivel de energía más bajo es no degenerado, y\(S_0=0\); entonces tenemos

\[S=-Nk\sum^{\infty }_{i=1}{P_i}\ln \rho \left(\epsilon_i\right) \]

Esta es la entropía de un sistema de\(N\) -molécula, volumen constante, temperatura constante que está en contacto térmico con su entorno a la misma temperatura. Obtenemos este mismo resultado en las Secciones 20.10 y 20.14 por argumentos en los que asumimos que el sistema está aislado. En todos estos argumentos, asumimos que el sistema de temperatura constante y su contraparte aislada son funcionalmente equivalentes; es decir, un grupo de conjuntos poblacionales que da cuenta de casi toda la probabilidad en un sistema también representa casi toda la probabilidad en el otro.

Debido a que obtenemos este resultado asumiendo que el sistema está compuesto por moléculas distinguibles independientes\(N\), no interaccionantes, la entropía de este sistema es\(N\) veces la contribución de entropía de una molécula individual. Podemos escribir

\[S_{\mathrm{molecule}}=-k\sum^{\infty }_{i=1}{P_i}\ln \rho \left(\epsilon_i\right) \]