4.4: Derivación de la Declaración Matemática de la Segunda Ley
- Page ID
- 78006
4.4.1 La existencia de la función de entropía
Esta sección deriva la existencia y propiedades de la función de estado llamada entropía.
Considerar un proceso cíclico arbitrario de un sistema cerrado. Para evitar confusiones, este sistema será el “sistema experimental” y el proceso será el “proceso experimental” o “ciclo experimental”. No hay restricciones sobre los contenidos del sistema experimental, puede tener algún grado de complejidad. El proceso experimental puede involucrar más de un tipo de trabajo, pueden ocurrir cambios de fase y reacciones, puede haber gradientes de temperatura y presión, pueden estar presentes restricciones y campos externos, y así sucesivamente. Todas las partes del proceso deben ser irreversibles o reversibles, pero no imposibles.
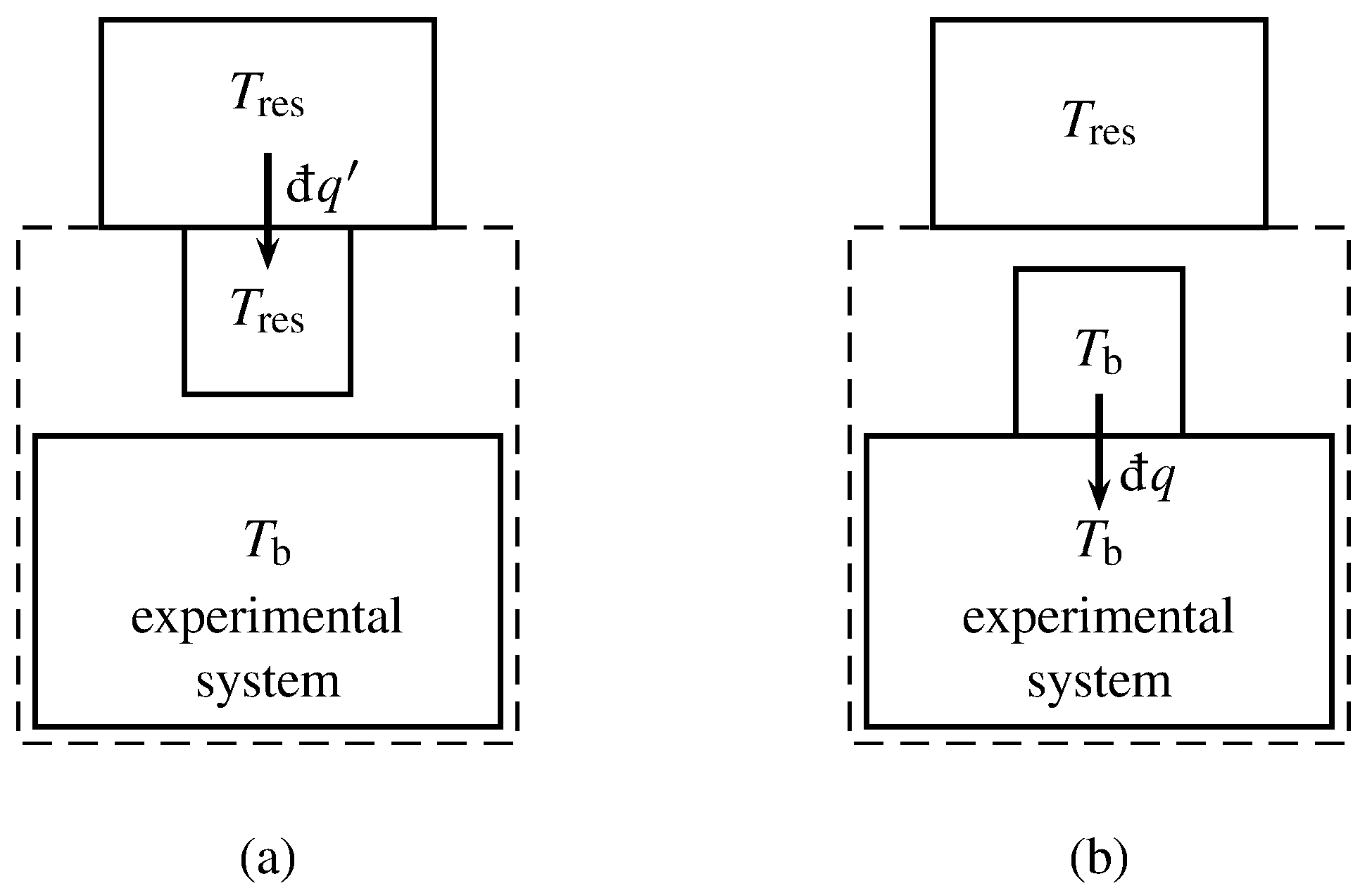
Figura 4.8 Sistema experimental, motor Carnot (representado por una pequeña caja cuadrada) y depósito de calor. Las líneas discontinuas indican el límite del supersistema.
(a) Transferencia de calor reversible entre el depósito de calor y el motor Carnot.
b) Transferencia de calor entre el motor Carnot y el sistema experimental.
Las cantidades infinitesimales\(\dq'\) y\(\dq\) son positivas para la transferencia en las direcciones indicadas por las flechas.
Imaginamos que el ciclo experimental se lleva a cabo de una manera especial que nos permite aplicar la declaración Kelvin—Planck de la segunda ley. El calor transferido a través del límite del sistema experimental en cada elemento de trayectoria infinitesimal del ciclo se intercambia con un hipotético motor Carnot. La combinación del sistema experimental y el motor Carnot es un supersistema cerrado (ver Fig. 4.8). En los alrededores del supersistema se encuentra un reservorio de calor de temperatura constante arbitraria\(T\subs{res}\). Al permitir que el supersistema intercambie calor solo con este único reservorio de calor, podremos aplicar la declaración Kelvin—Planck a un ciclo del supersistema.
Este procedimiento es similar a los descritos por A. B. Pippard (Elements of Classical Thermodynamics for Advanced Students of Physics, Cambridge University Press, Cambridge, 1966, cap. 4); C. J. Adkins (Equilibrium Thermodynamics, 3a edición, Cambridge University Press, Cambridge, 1983 , Cap. 5); y Peter T. Landsberg (Thermodynamics and Statistical Mechanics, Dover Publications, Inc., Nueva York, 1990, p. 53).
Suponemos que somos capaces de controlar los cambios de las coordenadas de trabajo del sistema experimental desde el entorno del supersistema. También podemos controlar el motor Carnot desde estos alrededores, por ejemplo moviendo el pistón de un dispositivo de cilindro-y-pistón que contiene la sustancia de trabajo. Así, la energía transferida por el trabajo a través del límite del sistema experimental, y el trabajo requerido para operar el motor Carnot, se intercambia con el entorno del supersistema.
Durante cada etapa del proceso experimental con calor distinto de cero, permitimos que el motor Carnot se someta a muchos ciclos infinitesimales de Carnot con cantidades infinitesimales de calor y trabajo. En uno de los pasos isotérmicos de cada ciclo de Carnot, el motor Carnot se encuentra en contacto térmico con el reservorio de calor, como se representa en la Fig. 4.8 (a). En este paso el motor Carnot tiene la misma temperatura que el depósito de calor, e intercambia calor reversiblemente\(\dq'\) con él. La convención de señal es que\(\dq'\) es positiva si el calor se transfiere en la dirección de la flecha, desde el depósito de calor hasta el motor Carnot.
En la otra etapa isotérmica del ciclo Carnot, el motor Carnot está en contacto térmico con el sistema experimental en una porción de los límites del sistema como se representa en la Fig. 4.8 (b). El motor Carnot tiene ahora la misma temperatura,\(T\bd\), que el sistema experimental en esta parte del límite, e intercambia calor con él. El calor\(\dq\) es positivo si la transferencia es al sistema experimental.
La relación entre temperaturas y calores en las etapas isotérmicas de un ciclo de Carnot viene dada por la Ec. 4.3.15. De esta relación obtenemos, para un ciclo infinitesimal de Carnot, la relación\(T\bd/T\subs{res}=\dq/\dq'\), o\ begin {ecuación}\ dQ'=T\ subs {res}\ frac {\ dq} {T\ bd}\ tag {4.4.1}\ end {ecuación}
Después de muchos ciclos infinitesimales de Carnot, el ciclo experimental está completo, el sistema experimental ha vuelto a su estado inicial y el motor Carnot ha vuelto a su estado inicial en contacto térmico con el reservorio de calor. La integración de la Ec. 4.4.1 alrededor del ciclo experimental da el calor neto que ingresa al supersistema durante el proceso:\ begin {join} Q'=T\ subs {res}\ tag {4.4.2}\ oint\! \ frac {\ dq} {T\ bd}\ end {reúnen} La integración aquí es sobre cada elemento path del proceso experimental y sobre cada elemento superficial del límite del sistema experimental.
Hay que tener en cuenta que el valor de la integral cíclica\(\oint\dq/T\bd\) depende únicamente de la trayectoria del ciclo experimental, que este proceso puede ser reversible o irreversible, y esa\(T\subs{res}\) es una constante positiva.
En este ciclo experimental, ¿podría ser positivo el calor neto\(q'\) transferido al supersistema? De ser así, el trabajo neto sería negativo (para hacer cero el cambio de energía interna) y el supersistema habría convertido completamente el calor de un único reservorio de calor en obra, un proceso que la declaración Kelvin—Planck de la segunda ley dice que es imposible. Por lo tanto es imposible que sea positivo, y\(q'\) a partir de la Ecuación 4.4.2 obtenemos la relación\ comenzar {reunir}\ s {\ oint\! \ frac {\ dq} {T\ bd}\ leq 0}\ tag {4.4.3}\ cond {(proceso cíclico de un sistema cerrado)}\ end {reunir} Esta relación se conoce como la desigualdad de Clausius. Solo es válido si la integración se toma alrededor de un camino cíclico en una dirección con nada más que cambios reversibles e irreversibles, el camino no debe incluir un cambio imposible, como el reverso de un cambio irreversible. La desigualdad Clausius dice que si un camino cíclico cumple con esta especificación, es imposible que la integral cíclica\(\oint(\dq/T\bd)\) sea positiva.
Si todo el ciclo experimental es adiabático (lo cual solo es posible si el proceso es reversible), no se necesita el motor Carnot y la Ec. 4.4.3 puede ser reemplazada por\(\oint(\dq/T\bd)=0\).
A continuación investiguemos un proceso no adiabático reversible del sistema experimental cerrado. Partiendo de un determinado estado de equilibrio A, llevamos a cabo un proceso reversible en el que hay un flujo neto de calor hacia el sistema, y en el que\(\dq\) es positivo o cero en cada elemento de trayectoria. El estado final de este proceso es el estado de equilibrio B. Si cada cantidad infinitesimal de calor\(\dq\) es positiva o cero durante el proceso, entonces la integral\(\int_{\tx{A}}^{\tx{B}}(\dq/T\bd)\) debe ser positiva. En este caso la desigualdad Clausius nos dice que si el sistema completa un ciclo volviendo del estado B de nuevo al estado A por un camino diferente, la integral\(\int_{\tx{B}}^{\tx{A}}(\dq/T\bd)\) para este segundo camino debe ser negativa. Por lo tanto, el cambio B\(\ra\) A no puede ser llevado a cabo por ningún proceso adiabático.
Cualquier proceso reversible se puede llevar a cabo a la inversa. Así, al invertir el proceso no adiabático reversible, es posible cambiar el estado de B a A mediante un proceso reversible con un flujo neto de calor fuera del sistema y con negativo\(\dq\) o cero en cada elemento de la trayectoria inversa. En contraste, la ausencia de una trayectoria adiabática de B a A significa que es imposible llevar a cabo el cambio A\(\ra\) B por un proceso adiabático reversible.
La regla general, entonces, es que siempre que el estado de equilibrio A de un sistema cerrado puede cambiarse al estado de equilibrio B mediante un proceso reversible con calor finito “unidireccional” (es decir, el flujo de calor está completamente dentro del sistema o completamente fuera de él), es imposible que el sistema cambie de cualquiera de estos estados al otro por un proceso adiabático reversible.
Un ejemplo sencillo relacionará esta regla con la experiencia. Podemos aumentar la temperatura de un líquido permitiendo que el calor fluya reversiblemente hacia el líquido. Es imposible duplicar este cambio de estado mediante un proceso reversible sin calor, es decir, usando algún tipo de trabajo reversible. La razón es que el trabajo reversible implica el cambio de una coordenada de trabajo que lleva al sistema a un estado final diferente. No hay nada en la regla que diga que no podemos aumentar la temperatura irreversiblemente sin calor, como podemos por ejemplo con el trabajo de agitación.
Los Estados A y B pueden estar arbitrariamente cercanos. Concluimos que cada estado de equilibrio de un sistema cerrado tiene otros estados de equilibrio infinitesimalmente cercanos a él que son inaccesibles por un proceso adiabático reversible. Este es el principio de inaccesibilidad adiabática de Carathéodory. (Constantin Carathéodory en 1909 combinó este principio con un teorema matemático El teorema de\(—\) Carathéodory\(—\) para deducir la existencia de la función de entropía. La derivación aquí esbozada evita las complejidades de ese tratamiento matemático y conduce a los mismos resultados.)
A continuación consideremos los procesos adiabáticos reversibles que son posibles. Para llevar a cabo un proceso adiabático reversible, partiendo de un estado de equilibrio inicial, utilizamos un límite adiabático y variamos lentamente una o más de las coordenadas de trabajo. Se obtendrá una cierta temperatura final. Es útil para visualizar este proceso pensar en un espacio\(N\) -dimensional en el que cada eje represente una de las variables\(N\) independientes necesarias para describir un estado de equilibrio. Un punto en este espacio representa un estado de equilibrio, y la trayectoria de un proceso reversible puede representarse como una curva en este espacio.
Un conjunto adecuado de variables independientes para estados de equilibrio de un sistema cerrado de temperatura uniforme consiste en la temperatura\(T\) y cada una de las coordenadas de trabajo (Sec. 3.10). Podemos variar las coordenadas de trabajo independientemente manteniendo el límite adiabático, por lo que los caminos para posibles procesos adiabáticos reversibles pueden conectar cualquier combinación arbitraria de valores de coordenadas de trabajo.
Sin embargo, existe la dimensión adicional de la temperatura en el espacio\(N\) -dimensional. ¿Los caminos para posibles procesos adiabáticos reversibles, partiendo de un punto inicial común, se encuentran en un volumen en el espacio\(N\) -dimensional? ¿O caen sobre una superficie descrita por\(T\) como una función de las coordenadas de trabajo? Si los caminos se encuentran en un volumen, entonces cada punto en un elemento de volumen que rodea el punto inicial debe ser accesible desde el punto inicial por una trayectoria adiabática reversible. Esta accesibilidad es precisamente lo que niega el principio de inaccesibilidad adiabática de Carathéodory. Por lo tanto, los caminos para todos los procesos adiabáticos reversibles posibles con un estado inicial común deben estar sobre una superficie única. Esta es una hipersuperficie\((N-1)\) -dimensional en el espacio\(N\) -dimensional, o una curva si\(N\) es\(2\). Una de estas superficies o curvas se denominará superficie adiabática reversible.
Ahora considere los estados inicial y final de un proceso reversible con calor unidireccional (es decir, cada cantidad infinitesimal distinta de cero de calor\(\dq\) tiene el mismo signo). Ya que hemos visto que es imposible que exista un camino adiabático reversible entre estos estados, los puntos para estos estados deben estar sobre diferentes superficies adiabáticas reversibles que no se crucen en ninguna parte del espacio\(N\) -dimensional. En consecuencia, hay un número infinito de superficies adiabáticas reversibles no intersecantes que llenan el espacio\(N\) -dimensional. (Para visualizar esto\(N=3\), piense en una pila flexionada de hojas de papel; cada hoja representa una superficie adiabática reversible diferente en el espacio tridimensional). Un proceso reversible no adiabático con calor unidireccional se representa por una trayectoria que comienza en un punto en una superficie adiabática reversible y termina en un punto en una superficie diferente. Si\(q\) es positivo, la superficie final se encuentra en un lado de la superficie inicial, y si\(q\) es negativa, la superficie final está en el lado opuesto.
4.4.2 Utilizar procesos reversibles para definir la entropía
La existencia de superficies adiabáticas reversibles es la justificación para definir una nueva función de estado\(S\), la entropía. \(S\)se especifica para tener el mismo valor en todas partes en una de estas superficies, y un valor diferente y único en cada superficie diferente. En otras palabras, las superficies adiabáticas reversibles son superficies de entropía constante en el espacio\(N\) -dimensional. El hecho de que las superficies llenen este espacio sin intersecarse asegura que\(S\) es una función de estado para estados de equilibrio, porque cualquier punto en este espacio representa un estado de equilibrio y también se encuentra sobre una sola superficie adiabática reversible con un valor definido de\(S\).
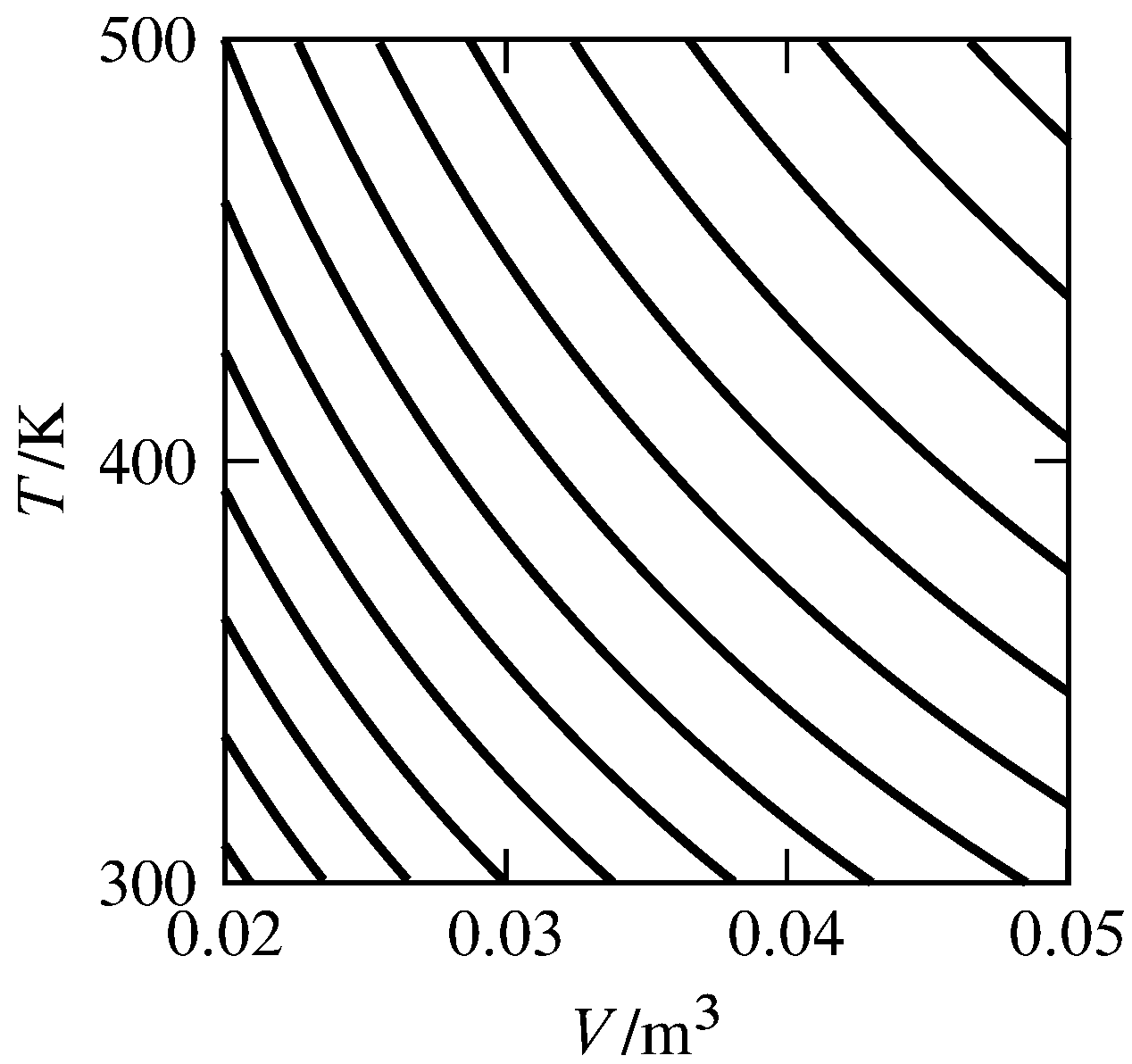
Figura 4.9 Familia de curvas adiabáticas reversibles (superficies adiabáticas reversibles bidimensionales) para un gas ideal con\(V\) y\(T\) como variables independientes. Un proceso adiabático reversible mueve el estado del sistema a lo largo de una curva, mientras que un proceso reversible con calor positivo mueve el estado de una curva a otra arriba y a la derecha. Las curvas se calculan para\(n = 1\mol\) y\(\CVm = (3/2)R\). Las curvas adyacentes difieren en entropía por\(1\units{J K\(^{-1}\)}\).
Sabemos que la función de entropía debe existir, porque existen las superficies adiabáticas reversibles. Por ejemplo, la Fig. 4.9 muestra una familia de estas superficies para un sistema cerrado de una sustancia pura en una sola fase. En este sistema,\(N\) es igual a 2, y las superficies son curvas bidimensionales. Cada curva es un contorno de constante\(S\). En esta etapa de la derivación, nuestra asignación de valores de\(S\) a las diferentes curvas es totalmente arbitraria.
¿Cómo podemos asignar un valor único de\(S\) a cada superficie adiabática reversible? Podemos ordenar los valores dejando que un proceso reversible con calor positivo unidireccional, que mueve el punto para el estado a una nueva superficie, corresponda a un incremento en el valor de\(S\). El calor negativo unidireccional corresponderá entonces a la disminución\(S\). Podemos asignar un valor arbitrario a la entropía en una superficie adiabática reversible particular. (Para ello se utiliza la tercera ley de la termodinámica, ver Sec. 6.1.) Entonces todo lo que se necesita para asignar un valor de\(S\) a cada estado de equilibrio es una fórmula para evaluar la diferencia en las entropías de dos superficies cualesquiera.
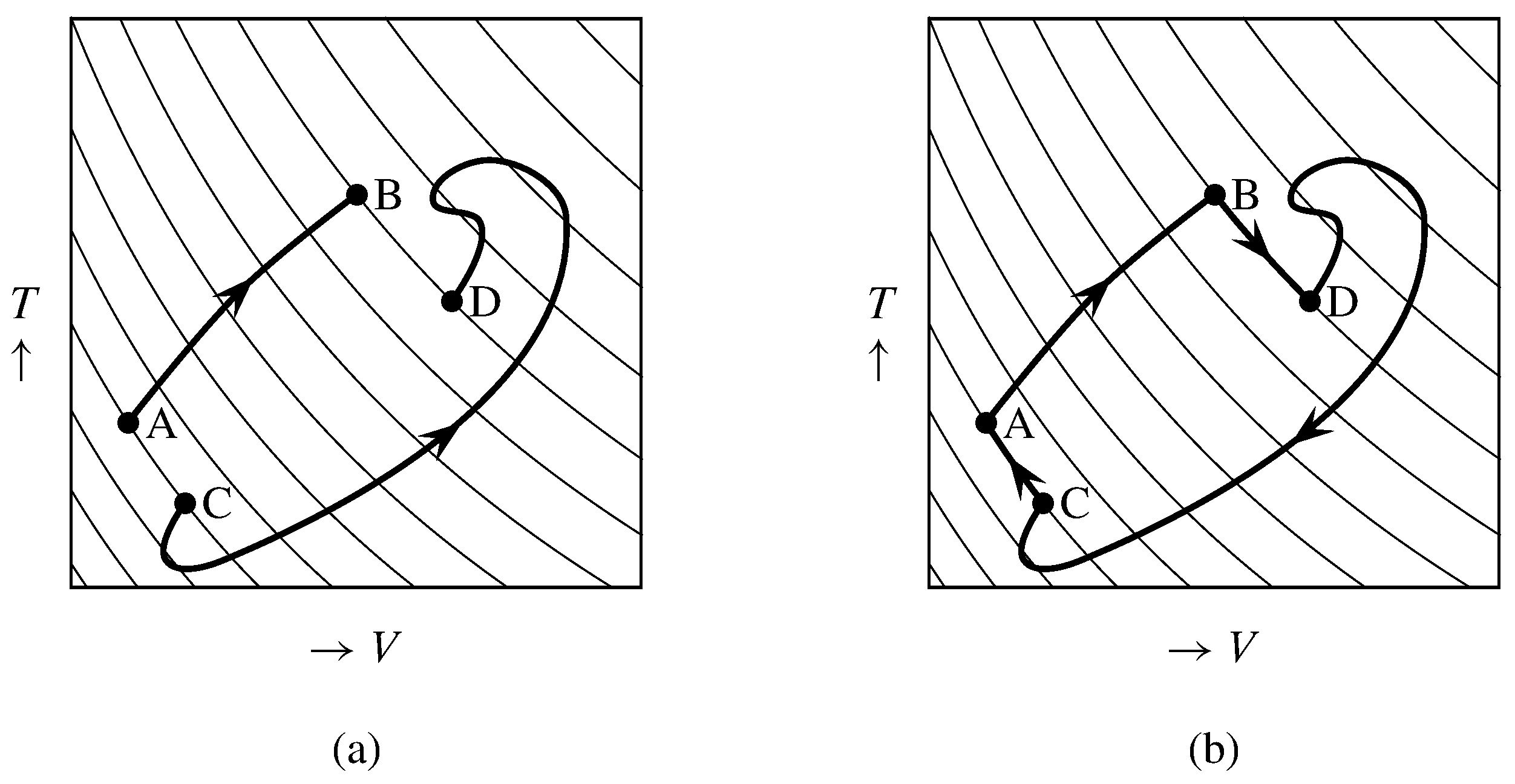
Figura 4.10 Caminos reversibles en\(V\) —\(T\) espacio. Las curvas delgadas son superficies adiabáticas reversibles.
a) Dos caminos que conectan el mismo par de superficies adiabáticas reversibles.
(b) Una trayectoria cíclica.
Considerar un proceso reversible con calor positivo unidireccional que cambie el sistema del estado A al estado B. El camino para este proceso debe mover el sistema de una superficie adiabática reversible de cierta entropía a una superficie diferente de mayor entropía. Un ejemplo es el camino A\(\ra\) B en la Fig. 4.10 (a). (Las superficies adiabáticas en esta figura son en realidad curvas bidimensionales). Como antes, combinamos el sistema experimental con un motor Carnot para formar un supersistema que intercambia calor con un único reservorio de calor de temperatura constante\(T\subs{res}\). El calor neto entrando al supersistema, encontrado al integrar la Ecuación 4.4.1, es\ begin {ecuación} q' = T\ subs {res}\ int_ {\ tx {A}} ^ {\ tx {B}}\ frac {\ dq} {T\ bd}\ tag {4.4.4}\ end {ecuación} y es positivo.
Supongamos que el mismo sistema experimental experimenta un segundo proceso reversible, no necesariamente con calor unidireccional, a lo largo de una trayectoria diferente que conecta el mismo par de superficies adiabáticas reversibles. Esta podría ser la ruta C\(\ra\) D en la Fig. 4.10 (a). El calor neto que ingresa al supersistema durante este segundo proceso es\(q''\):\ begin {equation} q” = T\ subs {res}\ int_ {\ tx {C}} ^ {\ tx {D}}\ frac {\ dq} {T\ bd}\ tag {4.4.5}\ end {ecuación} Podemos entonces idear un ciclo del supersistema en el que el sistema experimental se somete a la ruta reversible A \(\ra\)B\(\ra\) D\(\ra\) C\(\ra\) A, como se muestra en la Fig. 4.10 (b). La etapa A\(\ra\) B es el primer proceso descrito anteriormente, la etapa D\(\ra\) C es la inversa del segundo proceso descrito anteriormente, y las etapas B\(\ra\) D y C\(\ra\) A son reversibles y adiabáticas. El calor neto que ingresa al supersistema en el ciclo es\(q' - q''\). En el ciclo inverso el calor neto es\(q''-q'\). En ambos ciclos el calor se intercambia con un único reservorio de calor; por lo tanto, según la declaración Kelvin—Planck, ninguno de los ciclos puede tener calor neto positivo. Por lo tanto\(q'\) y\(q''\) debe ser igual, y las ecuaciones 4.4.4 y 4.4.5 luego muestran que la integral\(\int(\dq/T\bd)\) tiene el mismo valor cuando se evalúa a lo largo de cualquiera de las trayectorias reversibles desde la superficie de entropía inferior a la superior.
Obsérvese que dado que la segunda trayectoria (C\(\ra\) D) no necesariamente tiene calor unidireccional, puede tomar el sistema experimental a través de cualquier secuencia de valores de entropía intermedios, siempre que comience en la superficie de entropía inferior y termine en la más alta. Además, dado que el camino es reversible, se puede llevar a cabo a la inversa dando como resultado la inversión de los signos de\(\Del S\) y\(\int(\dq/T\bd)\).
Ahora debería ser evidente que una fórmula satisfactoria para definir el cambio de entropía de un proceso reversible en un sistema cerrado es\ begin {recopilar}\ s {\ Del S =\ int\! \ frac {\ dq} {T\ bd}}\ tag {4.4.6}\ cond {(proceso reversible,}\ nextcond {sistema cerrado)}\ end {recopilar} Esta fórmula satisface los requisitos necesarios: hace que el valor de\(\Del S\) positivo si el proceso tiene calor positivo unidireccional, negativo si el proceso tiene calor negativo unidireccional, y cero si el proceso es adiabático. Da el mismo valor de\(\Del S\) para cualquier cambio reversible entre las mismas dos superficies adiabáticas reversibles, y hace que la suma de los\(\Del S\) valores de varios procesos reversibles consecutivos sea igual a\(\Del S\) para el proceso general.
En la Ecuación 4.4.6,\(\Del S\) se encuentra el cambio de entropía cuando el sistema cambia de un estado de equilibrio arbitrario a otro. Si el cambio es un elemento de ruta infinitesimal de un proceso reversible, la ecuación se convierte en\ begin {recopilar}\ s {\ dif S =\ frac {\ dq} {T\ bd}}\ tag {4.4.7}\ cond {(proceso reversible,}\ nextcond {sistema cerrado)}\ end {recopilar} Es común ver esta ecuación escrita en la forma\(\dif S = \dq\rev/T\), donde\(\dq\rev\) denota un cantidad infinitesimal de calor en un proceso reversible.
En la Ecuación 4.4.7, la cantidad\(1/T\bd\) se denomina factor integrador for\(\dq\), factor que hace que el producto\((1/T\bd)\dq\) sea el cambio infinitesimal de una función de estado. La cantidad\(c/T\bd\), donde\(c\) está cualquier constante distinta de cero, también sería un factor integrador satisfactorio; por lo que la definición de entropía, utilizando\(c{=}1\), es en realidad una de un número infinito de opciones posibles para asignar valores a las superficies adiabáticas reversibles.
4.4.3 Algunas propiedades de la entropía
No es difícil demostrar que la entropía de un sistema cerrado en estado de equilibrio es una propiedad extensa. Supongamos que un sistema de temperatura uniforme\(T\) se divide en dos subsistemas cerrados A y B. Cuando se produce un cambio infinitesimal reversible, los cambios de entropía de los subsistemas son\(\dif S\subs{A} = \dq\subs{A}/T\)\(\dif S\subs{B} = \dq\subs{B}/T\) y y del sistema\(\dif S = \dq/T\). Pero\(\dq\) es la suma de\(\dq\subs{A}\) y\(\dq\subs{B}\), que da\(\dif S = \dif S\subs{A} + \dif S\subs{B}\). Así, los cambios de entropía son aditivos, por lo que la entropía debe ser extensa:\(S=S\subs{A}+S\subs{B}\). (El argumento no es del todo completo, porque no hemos demostrado que cuando cada subsistema tiene una entropía de cero, también lo hace todo el sistema. El cero de entropía se discutirá en la Sec. 6.1.)
¿Cómo podemos evaluar la entropía de un estado de equilibrio particular del sistema? Debemos asignar un valor arbitrario a un estado y luego evaluar el cambio de entropía a lo largo de un camino reversible desde este estado al estado de interés utilizando\(\Del S=\int(\dq/T\bd)\).
Es posible que necesitemos evaluar la entropía de un estado de no equilibrio. Para ello, imaginamos imponer restricciones internas hipotéticas que cambian el estado de no equilibrio a un estado de equilibrio restringido con la misma estructura interna. Algunos ejemplos de tales restricciones internas se dieron en la Sec. 2.4.4, e incluyen particiones adiabáticas rígidas entre fases de diferente temperatura y presión, membranas semipermeables para evitar la transferencia de ciertas especies entre fases adyacentes e inhibidores para prevenir reacciones químicas.
Suponemos que podemos, en principio, imponer o eliminar dichas restricciones de manera reversible sin calor, por lo que no hay cambio de entropía. Si el estado de no equilibrio incluye movimiento interno macroscópico, la imposición de restricciones internas implica un trabajo reversible negativo para que las regiones móviles del sistema descansen. Este concepto equivale a definir la entropía de un estado con movimiento interno macroscópico para que sea la misma que la entropía de un estado con la misma estructura interna pero sin el movimiento, es decir, el mismo estado congelado en el tiempo. Por esta definición,\(\Del S\) para un proceso puramente mecánico (Sec. 3.2.3) es cero.
Si el sistema no es uniforme en su extensión, las restricciones internas lo dividirán en regiones prácticamente uniformes cuya entropía es aditiva. La entropía del estado de no equilibrio se encuentra a partir del\(\Del S=\int(\dq/T\bd)\) uso de un camino reversible que cambia el sistema de un estado de equilibrio de entropía conocida al estado de equilibrio restringido con la misma entropía que el estado de interés. Este procedimiento permite que cada estado posible (al menos conceptualmente) tenga un valor definido de\(S\).


