4.5: Procesos irreversibles

Template:DeVoeMathJax

Sabemos que durante un proceso reversible de un sistema cerrado, cada cambio de entropía infinitesimal\(\dif S\) es igual a\(\dq/T\bd\) y el cambio finito\(\Del S\) es igual a lo integral\(\int(\dq/T\bd)\), pero ¿qué podemos decir sobre\(\dif S\) y\(\Del S\) para un proceso irreversible?

La derivación de esta sección mostrará que para un cambio irreversible infinitesimal de un sistema cerrado,\(\dif S\) es mayor que\(\dq/T\bd\), y para todo un proceso\(\Del S\) es mayor que\(\int(\dq/T\bd)\). Es decir, las igualdades que se aplican a un proceso reversible son reemplazadas, por un proceso irreversible, por desigualdades.

La derivación comienza con procesos irreversibles que son adiabáticos, y luego se extiende a procesos irreversibles en general.

4.5.1 Procesos adiabáticos irreversibles

Considerar un proceso adiabático irreversible arbitrario de un sistema cerrado comenzando con un estado inicial particular A. El estado final B depende de la trayectoria de este proceso. Deseamos investigar el signo del cambio de entropía\(\Del S\subs{A\(\ra\) B}\). Nuestro razonamiento dependerá de si hay o no trabajo durante el proceso.

Si hay trabajo a lo largo de algún elemento de trayectoria infinitesimal del proceso adiabático irreversible (\(\dw \ne 0\)), sabemos por experiencia que este trabajo sería diferente si la coordenada o coordenadas de trabajo cambiaran a un ritmo diferente, porque la disipación de energía de la fricción interna sería entonces diferente. En el límite de la lentitud infinita, un proceso adiabático con estado inicial A y el mismo cambio de coordenadas de trabajo se volvería reversible, y el trabajo neto y la energía interna final diferirían de los del proceso irreversible. Debido a que el estado final del proceso adiabático reversible es diferente del B, no existe una trayectoria adiabática reversible con trabajo entre los estados A y B.

Todos los estados de un proceso reversible, incluyendo los estados inicial y final, deben ser estados de equilibrio. Por lo tanto, existe una dificultad conceptual para considerar caminos reversibles entre dos estados si alguno de estos estados son estados de no equilibrio. En tal caso asumiremos que el estado ha sido sustituido por un estado de equilibrio restringido de la misma entropía como se describe en la Sec. 4.4.3.

Si, por otro lado, no hay trabajo a lo largo de ningún elemento de trayectoria infinitesimal del proceso adiabático irreversible (\(\dw{=}0\)), el proceso se está llevando a cabo a energía interna constante\(U\) en un sistema aislado. No se puede alcanzar un límite reversible sin calor o trabajo (Sec. 3.2.1). Por lo tanto, cualquier cambio adiabático reversible del estado A requeriría trabajo, provocando un cambio\(U\) e impidiendo que el sistema alcance el estado B por cualquier trayectoria adiabática reversible.

Entonces, independientemente de que un proceso adiabático irreversible A\(\ra\) B implique o no trabajo, no existe un camino adiabático reversible entre A y B. Los únicos caminos reversibles entre estos estados deben ser no adiabáticos. De ello se deduce que el cambio de entropía\(\Del S\subs{A\(\ra\) B}\), dado por el valor de\(\dq/T\bd\) integrado sobre una ruta reversible de A a B, no puede ser cero.

A continuación nos preguntamos si\(\Del S\subs{A\(\ra\) B}\) podría ser negativo. En cada camino infinitesimal elemento del proceso adiabático irreversible A\(\ra\) B,\(\dq\) es cero y la integral\(\int_{\tx{A}}^{\tx{B}}(\dq/T\bd)\) a lo largo de la trayectoria de este proceso es cero. Supongamos que el sistema completa un ciclo regresando por un camino diferente y reversible del estado B de regreso al estado A. La desigualdad de Clausius (Ec. 4.4.3) nos dice que en este caso la integral\(\int_{\tx{B}}^{\tx{A}}(\dq/T\bd)\) a lo largo del camino reversible no puede ser positiva. Pero esta integral para el camino reversible es igual a\(-\Del S\subs{A\(\ra\) B}\), así que\(\Del S\subs{A\(\ra\) B}\) no puede ser negativa.

Se concluye que debido a que el cambio de entropía del proceso adiabático irreversible A\(\ra\) B no puede ser cero, y no puede ser negativo, debe ser positivo.

En esta derivación, el estado inicial A es arbitrario y el estado final B se alcanza mediante un proceso adiabático irreversible. Si los dos estados son infinitesimalmente diferentes, entonces el cambio es infinitesimal. Así, para un cambio infinitesimal que sea irreversible y adiabático,\(\dif S\) debe ser positivo.

4.5.2 Procesos irreversibles en general

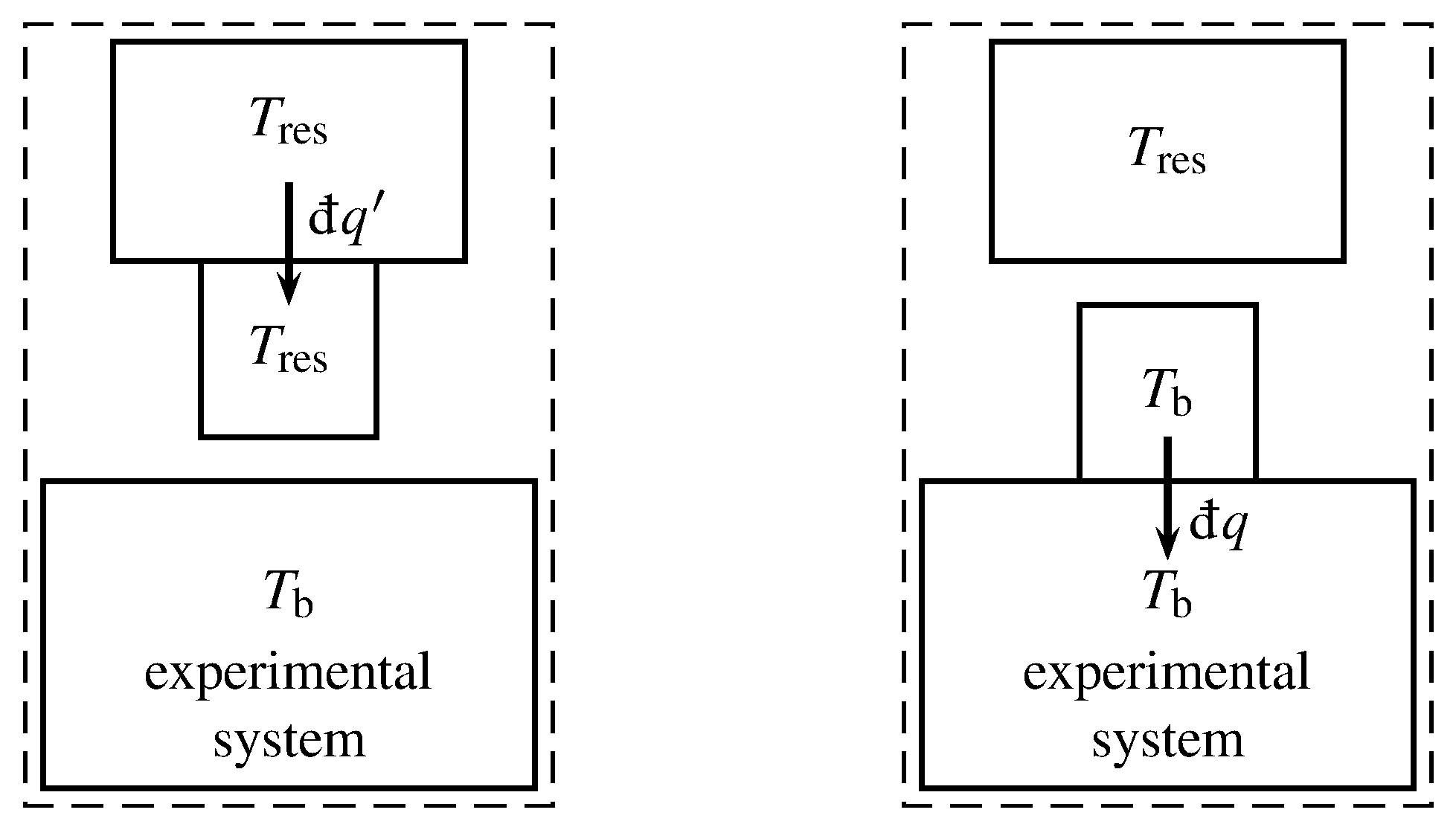
Figura 4.11 Supersystem que incluye el sistema experimental, un motor Carnot (caja cuadrada) y un reservorio de calor. El rectángulo discontinuo indica el límite del supersistema.

Para tratar un proceso irreversible de un sistema cerrado que no es adiabático, se procede de la siguiente manera. Al igual que en la Sec. 4.4.1, utilizamos un motor Carnot para la transferencia de calor a través del límite del sistema experimental. Movemos el límite del supersistema de la Fig. 4.8 de manera que el supersistema ahora incluye el sistema experimental, el motor Carnot, y un reservorio de calor de temperatura constante\(T\subs{res}\), como se representa en la Fig. 4.11. Durante un cambio irreversible del sistema experimental, el motor Carnot sufre muchos ciclos infinitesimales. Durante cada ciclo, el motor Carnot\(\dq'\) intercambia calor a temperatura\(T\subs{res}\) con el reservorio de calor y calor\(\dq\) a temperatura\(T\bd\) con el sistema experimental, como se indica en la figura. Utilizamos la convención de señal que\(\dq'\) es positiva si el calor se transfiere al motor Carnot, y\(\dq\) es positivo si el calor se transfiere al sistema experimental, en las direcciones de las flechas en la figura.

Los intercambios de supersistemas funcionan, pero no el calor, con su entorno. Durante un ciclo infinitesimal del motor Carnot, el cambio neto de entropía del motor Carnot es cero, el cambio de entropía del sistema experimental es\(\dif S\), el calor transferido entre el motor Carnot y el sistema experimental es\(\dq\), y el calor transferido entre el depósito de calor y el motor Carnot viene dado por\(\dq'=T\subs{res}\dq/T\bd\) (Ec. 4.4.1). La transferencia de calor entre el depósito de calor y el motor Carnot es reversible, por lo que el cambio de entropía del depósito de calor es\ begin {ecuación}\ dif S\ subs {res} = -\ frac {\ dq'} {T\ subs {res}} = -\ frac {\ dq} {T\ bd}\ tag {4.5.1}\ end {ecuación} El cambio de entropía de la superyínea es la suma de los cambios de entropía de su partes:\ begin {ecuación}\ dif S\ subs {ss} =\ dif S +\ dif S\ subs {res} =\ dif S -\ frac {\ dq} {T\ bd}\ tag {4.5.2}\ end {ecuación} El proceso dentro del supersistema es adiabático e incluye un cambio irreversible dentro del sistema experimental, por lo que según las conclusiones del Sec. 4.5.1,\(\dif S\subs{ss}\) es positivo. La ecuación 4.5.2 muestra entonces que\(\dif S\), el cambio de entropía infinitesimal durante el cambio irreversible del sistema experimental, debe ser mayor que\(\dq/T\bd\):\ begin {recopilar}\ s {\ dif S >\ frac {\ dq} {T\ bd}}\ tag {4.5.3}\ cond {(cambio irreversible, sistema cerrado)}\ end {reúnen} Esta relación incluye el caso de un cambio adiabático irreversible, porque muestra que si\(\dq\) es cero,\(\dif S\) es mayor que cero.

Al integrar ambos lados de la ecuación 4.5.3 entre los estados inicial y final del proceso irreversible, obtenemos una relación para el cambio de entropía finito correspondiente a muchos ciclos infinitesimales del motor Carnot:\ begin {recopilar}\ s {\ Del S >\ int\! \ frac {\ dq} {T\ bd}}\ tag {4.5.4}\ cond {(proceso irreversible, sistema cerrado)}\ end {reunir}