1.3: Modelos mecánicos cuánticos básicos

En esta sección se resumen los resultados que surgen para modelos comunes para objetos mecánicos cuánticos. Estos forman el punto de partida para describir el movimiento de los electrones y los movimientos traslacionales, rotacionales y vibracionales de las moléculas. Por lo tanto, son la base para desarrollar la intuición sobre problemas más complejos.

Olas

Las ondas forman la base de nuestra descripción mecánica cuántica de la materia. Las ondas describen la amplitud oscilatoria de la materia y los campos en el tiempo y el espacio, y pueden tomar varias formas. La forma más simple que usaremos son las ondas planas, que se pueden escribir como

\[\psi ( \mathbf {r} , t ) = \mathbf {A} \exp [ i \mathbf {k} \cdot \mathbf {r} - \mathbf {i} \omega t ] \label{43}\]

La frecuencia angular\(ω\) describe las oscilaciones en el tiempo y está relacionada con el número de ciclos por segundo a través\(ν = ω/2π\). La amplitud de onda también varía en el espacio según lo determina el evector de ondas\(\mathbf {k}\), donde está el número de ciclos por unidad de distancia (longitud de onda)\(λ = ω/k\). Así, la onda se propaga en tiempo y espacio a lo largo de una dirección\(\mathbf {k}\) con una amplitud vectorial A con una velocidad de fase\(vϕ = νλ\).

Partículas Libres

Para una partícula libre de masa\(m\) en una dimensión, el hamiltoniano solo refleja la energía cinética de la partícula

\[\hat {H} = \hat {T} = \frac {\hat {p}^{2}} {2 m} \label{44}\]

A juzgar por la forma funcional del operador de impulso, asumimos que las funciones de onda tendrán la forma de ondas planas

\[\psi (x) = A e^{i k x} \label{45}\]

Insertando esta expresión en el TISE, eq. (1.1.6), encontramos que

\[k = \sqrt {\frac {2 m E} {\hbar^{2}}} \label{46}\]

y establecer\(A = 1 / \sqrt {2 \pi}\). Ahora, como sabemos eso\(E = p^{2} / 2 m\), podemos escribir

\[k = \frac {p} {\hbar} \label{47}\]

\(k\)es el evector de ondas, que equiparamos con el impulso de la partícula.

Las ondas de plano de partículas libres\(\psi _ {k} (x)\) forman un conjunto de bases completo y continuo con el que describir la función de onda. Tenga en cuenta que las funciones propias, Ecuación (\ ref {45}), son oscilatorias en todo el espacio. Por lo tanto, describir una onda plana permite especificar exactamente el vector de onda o el momento de la partícula, pero no se puede localizarla en ningún punto del espacio. De esta forma, la partícula libre no es observable porque su función ondulada se extiende infinitamente y no puede normalizarse. Una observación, sin embargo, tomando un valor de expectativa de un operador hermitiano colapsará esta función de onda para producir un impulso promedio de la partícula con una relación de incertidumbre correspondiente a su posición.

Partículas unidas

Particle-in-a-Box

El modelo mínimo para el movimiento de traslación de una partícula que está confinada en el espacio viene dado por la partícula en una caja. Para el caso de una partícula confinada en una dimensión en una caja de longitud L con paredes impenetrables, definimos el hamiltoniano como

\[\hat {H} = \frac {\hat {p}^{2}} {2 m} + V (x) \label{48}\]

\[V (x) = \left\{\begin{array} {l l} {0} & {0 < x < L _ {x}} \\ {\infty} & {\text {otherwise}} \end{array} \right. \label{49}\]

Las condiciones límite requieren que la partícula no pueda tener ninguna probabilidad de estar dentro de la pared, por lo que la función de onda debe desaparecer en\(x = 0\) y\(L_x\), como con las ondas estacionarias. Por lo tanto, asumimos una solución en forma de función sinusoidal. Las funciones propias normalizadas correctamente son

\[\psi _ {n} = \sqrt {\frac {2} {L}} \sin \frac {n \pi x} {L} \quad n = 1,2,3 \dots \label{50}\]

Aquí\(n\) están los números cuánticos enteros que describen los armónicos de la frecuencia fundamental\(\pi/L\) cuyas oscilaciones encajarán en la caja mientras obedecen las condiciones límite. Vemos que cualquier estado de la partícula en una caja se puede expresar en una serie de Fourier. Al insertar la ecuación\ ref {50} en la ecuación de Schrödinger independiente del tiempo, encontramos los valores propios de energía

\[E _ {n} = \frac {n^{2} \pi^{2} h^{2}} {2 m L^{2}} \label{51}\]

Tenga en cuenta que la separación entre los niveles de energía adyacentes crece a medida que\(n(n+1)\). Este modelo se extiende fácilmente a una caja tridimensional separando la caja en\(x\),\(y\), y\(z\) coordenadas. Entonces

\[\hat {H} = \hat {H} _ {x} + \hat {H} _ {y} + \hat {H} _ {z} \label{52}\]

en el que cada término se especifica como Ecuación\ ref {48}. Ya que\(\hat {H} _ {x}\)\(\hat {H} _ {y}\),,\(\hat {H} _ {z}\) conmutar, cada dimensión es separable de las demás. Entonces encontramos

\[\psi ( x , y , z ) = \psi _ {x} \psi _ {y} \psi _ {z} \label{53}\]

y

\[E _ {x , y , z} = E _ {x} + E _ {y} + E _ {z} \label{54}\]

que siguen las definiciones dadas en la Ecuación\ ref {50} y\ ref {51} anteriores. El estado del sistema se especifica ahora por tres números cuánticos con valores enteros positivos:\(n_x\),\(n_y\),\(n_z\)

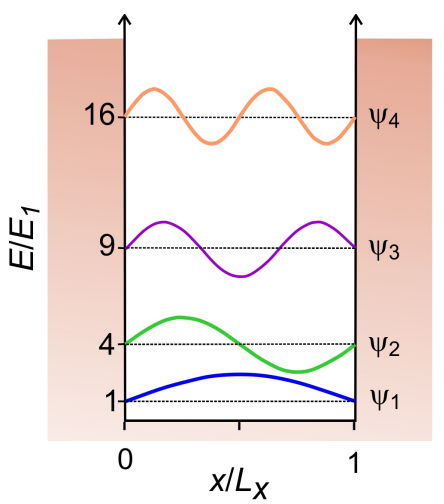
Figura 1. Fusiones de onda potenciales de partículas en una caja que se trazan superpuestas a sus niveles de energía correspondientes.

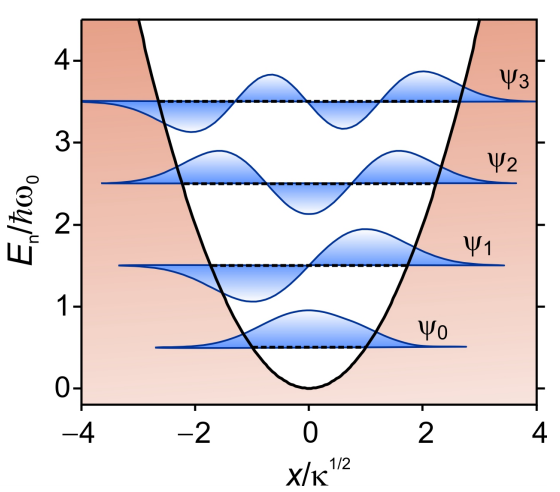
Figura 2. Potencial de oscilador armónico que muestra funciones de onda superpuestas a sus niveles de energía correspondientes.

Oscilador armónico

El oscilador armónico Hamiltoniano se refiere a una partícula confinada a un potencial parabólico o armónico. Lo usaremos para representar el movimiento vibracional en las moléculas, pero también se convierte en un marco general para entender todos los bosones. Para una partícula clásica unida en un potencial unidimensional, el potencial cercano al mínimo se\(x_0\) puede expandir como

\[V (x) = V \left( x _ {0} \right) + \left( \frac {\partial V} {\partial x} \right) _ {x = x _ {0}} \left( x - x _ {0} \right) + \frac {1} {2} \left( \frac {\partial V^{2}} {\partial x^{2}} \right) _ {x = x _ {0}} \left( x - x _ {0} \right)^{2} + \cdots \label{55}\]

Estableciendo\(x_0\) en 0, el término principal con una dependencia de\(x\) es el término de segundo orden (armónico)\(V = - \mathrm {K} x^{2} / 2\), donde la constante de fuerza

\[\kappa = - \left( \partial^{2} V / \partial x^{2} \right) _ {x = 0}.\]

El hamiltoniano clásico para una partícula de masa\(m\) confinada a este potencial es

\[H = \frac {p^{2}} {2 m} + \frac {1} {2} \kappa x^{2} \label{56}\]

Observando que la constante de fuerza y la frecuencia de oscilación están relacionadas por

\[\kappa = m \omega _ {0}^{2},\]

podemos sustituir operadores por\(p\) y\(x\) en Ecuación\ ref {56} para obtener el quántico hamiltoniano

\[\hat {H} = - \frac {1} {2} \frac {\hbar^{2}} {m} \frac {\partial^{2}} {\partial x^{2}} + \frac {1} {2} m \omega _ {0}^{2} \hat {x}^{2} \label{57}\]

También haremos uso de coordenadas ponderadas en masa reducidas definidas como

\[p = \sqrt {\frac {2} {m \hbar \omega _ {0}}} \hat {p}\label{58A}\]

\[x = \sqrt {\frac {m \omega _ {0}} {2 \hbar}} \hat {x} \label{58B}\]

para lo cual el hamiltoniano puede escribirse como

\[\hat {H} = \hbar \omega _ {0} \left( p^{2} + q^{2} \right) \label{59}\]

Los estados propios para el oscilador armónico se expresan en términos de polinomios hermitas

\[\psi _ {n} (x) = \sqrt {\frac {\alpha} {2^{n} \sqrt {\pi} n !}} e^{- \alpha^{2} x^{2} / 2} \mathcal {H} _ {n} ( \alpha x ) \label{60}\]

donde\(\alpha=\sqrt{m \omega_{0} / \hbar}\) y los polinomios hermitas se obtienen de

\[\mathcal {H} _ {n} (x) = ( - 1 )^{n} e^{x^{2}} \frac {d^{n}} {d x^{n}} e^{- x^{2}} \label{61}\]

Los valores propios de energía correspondientes están igualmente espaciados en unidades del cuántico vibracional\(\hbar \omega _ {0} \) por encima de la energía de punto cero\(\hbar \omega _ {0} / 2\).

\(E_{n}=\hbar \omega_{0}\left(n+\frac{1}{2}\right) \quad n=0,1,2 \ldots \label{62}\)

Operadores de elevación y descenso para osciladores armónicos

Desde un punto de vista práctico, será más útil para nosotros trabajar problemas que involucren osciladores armónicos en términos de operadores de subida y baja (también conocidos como operadores de creación y aniquilación, u operadores de escalera). Los definimos como

\[\hat {a} = \sqrt {\frac {2 \hbar} {m \omega _ {0}}} \left( \hat {x} + \frac {i} {m \omega _ {0}} \hat {p} \right) \label{63}\]

\[\hat {a}^{\dagger} = \sqrt {\frac {2 \hbar} {m \omega _ {0}}} \left( \hat {x} - \frac {i} {m \omega _ {0}} \hat {p} \right) \label{64}\]

Note\(a\) y\(a^†\) los operadores son conjugados hermitianos entre sí. Estos operadores obtienen su nombre de su acción sobre las funciones de onda del oscilador armónico, que es bajar o elevar el estado del sistema:

\[\hat {a} | n \rangle = \sqrt {n} | n - 1 \rangle \label{65}\]

y

\[\hat {a}^{\dagger} | n \rangle = \sqrt {n + 1} | n + 1 \rangle\]

Entonces encontramos que los operadores de posición e impulso son

\[\hat {x} = \sqrt {\frac {\hbar} {2 m \omega _ {0}}} \left( \hat {a}^{\dagger} + \hat {a} \right) \label{66}\]

\[\hat {p} = i \sqrt {\frac {m \hbar \omega _ {0}} {2}} \left( \hat {a}^{\dagger} - \hat {a} \right) \label{67}\]

Cuando sustituimos a estos operadores de escalera por los operadores de posición e impulso, conocidos como segunda cuantificación, el hamiltoniano se convierte en

\[\hat {H} = \hbar \omega _ {0} \left( \hat {n} + \frac {1} {2} \right) \label{68}\]

El operador numérico se define como\(\hat {n} = \hat {a}^{\dagger} \hat {a}\) y devuelve el estado del sistema:\(\hat {n} = \hat {a}^{\dagger} \hat {a}\). Los valores propios de energía\(\hat {H} | n \rangle = E _ {n} | n \rangle\) que satisfacen están dados por la Ecuación\ ref {62). Dado que los números cuánticos no pueden ser negativos, afirmamos una condición límite\(a | 0 \rangle = 0\), donde\(0\) se refiere al vector nulo. El oscilador armónico Hamiltoniano expresado en operadores de elevación y descenso, junto con su relación de conmutación

\[\left[ a , a^{\dagger} \right] = 1 \label{69}\]

se utiliza como representación general de todos los bosones, que para nuestros fines incluye vibraciones y fotones.

Propiedades de operadores de elevación y baja

\(a\)y\(a^†\) a operadores son conjugados hermitianos entre sí.

\[a a^{\dagger} + a^{\dagger} a = a^{\dagger} a + \frac {1} {2} \label{70}\]

\[\left[ a , a^{\dagger} \right] = 1 \label{71}\]

\[[ a , a ] = 0 \left[ a^{\dagger} , a^{\dagger} \right] = 0 \label{72}\]

\[\left[ a , \left( a^{\dagger} \right)^{n} \right] = n \left( a^{\dagger} \right)^{n - 1} \label{73}\]

\[\left[ a^{\dagger} , a^{n} \right] = - n a^{n - 1} \label{74}\]

\[| n \rangle = \frac {1} {\sqrt {n !}} \left( a^{\dagger} \right)^{n} | 0 \rangle \label{75}\]

Oscilador Morse

El oscilador Morse es un modelo para una partícula en una superficie de energía potencial anarmónica unidimensional con un límite disociativo a desplazamiento infinito. Se utiliza comúnmente para describir la espectroscopia de moléculas diatómicas y dinámicas vibracionales anarmónicas, y la mayoría de sus propiedades se pueden expresar a través de expresiones analíticas.3 El potencial de Morse es

\[V (x) = D _ {e} \left[ 1 - e^{- \alpha x} \right]^{2} \label{76}\]

donde\(x = \left( r - r _ {0} \right)\). \(D_e\)establece la profundidad del mínimo de energía en\(r = r_0\) relación con el límite de disociación como\(r → ∞\), y α establece la curvatura del potencial. Si nos expandimos\(V\) en potencias de\(x\) como se describe en la Ecuación\ ref {55}

\[V (x) \approx \frac {1} {2} \kappa x^{2} + \frac {1} {6} g x^{3} + \frac {1} {24} h x^{4} + \cdots \label{77}\]

encontramos que los coeficientes de expansión armónicos, cúbicos y cuárticos son

\[\kappa = 2 D _ {e} \alpha^{2},\]

\[g = - 6 D _ {e} \alpha^{3},\]

y\[h = 14 D _ {e} \alpha^{4}.\]

El oscilador Morse Hamiltoniano para una molécula diatómica de mR de masa reducida unida por este potencial es

\[H = \frac {p^{2}} {2 m _ {R}} + V (x) \label{78}\]

y tiene los valores propios

\[E _ {n} = \hbar \omega _ {0} \left[ \left( n + \frac {1} {2} \right) - x _ {e} \left( n + \frac {1} {2} \right)^{2} \right] \label{79}\]

Aquí\(\omega _ {0} = \sqrt {2 D _ {e} \alpha^{2} / m _ {R}}\) está la frecuencia fundamental y\(x _ {e} = \hbar \omega _ {0} / 4 D _ {e}\) es la constante anarmónica. Similar al oscilador armónico, la frecuencia\(\omega _ {0} = \sqrt {\kappa / m _ {R}}\). La constante anarmónica e x se ve comúnmente en la expresión espectroscópica para los niveles de energía vibratoria anarmónica

\[G ( v ) = \omega _ {e} \left( v + \frac {1} {2} \right) - \omega _ {e} x _ {e} \left( v + \frac {1} {2} \right)^{2} + \omega _ {e} y _ {e} \left( v + \frac {1} {2} \right)^{3} + \cdots \label{80}\]

De la ecuación\ ref {79}, la energía del estado fundamental (o punto cero) es

\[E _ {0} = \frac {1} {2} \hbar \omega _ {0} \left( 1 - \frac {1} {2} x _ {e} \right) \label{81}\]

Entonces la energía de disociación para el potencial Morse viene dada por\(D_{0}=D_{e}-E_{0}\). Las energías de transición son

\[E _ {n} - E _ {m} = \hbar \omega _ {0} ( n - m ) \left[ 1 - x _ {e} \left( n + m + \frac {1} {2} \right) \right] \label{82}\]

Las expresiones armónicas adecuadas se obtienen de las expresiones correspondientes del oscilador Morse configurando\(D _ {e} \rightarrow \infty\) o\(x _ {e} \rightarrow 0\).

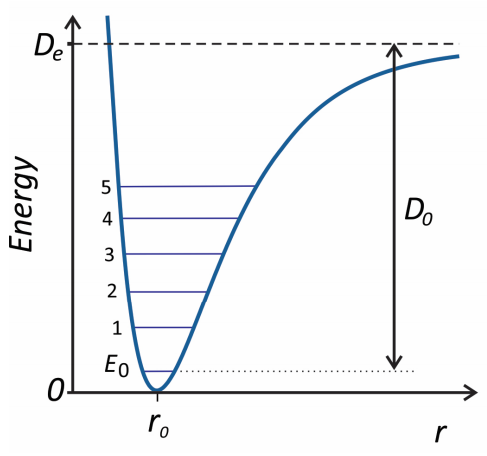
Figura 3. Forma del potencial Morse que ilustra los primeros seis valores propios de energía.

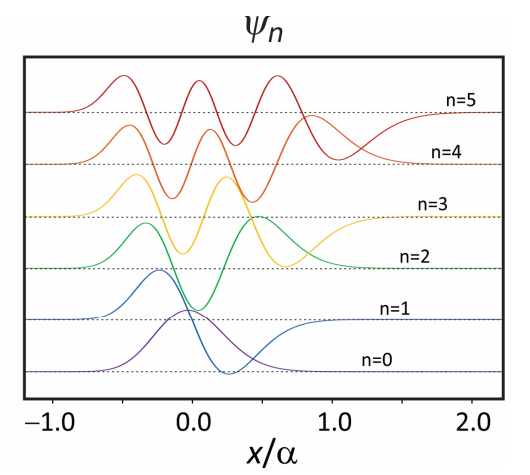
Figura 4. Las primeras seis funciones propias del potencial del oscilador Morse.

Las funciones de onda para el oscilador Morse también pueden expresar analíticamente en términos de polinomios asociados de Laguerre\(\mathcal {L} _ {n}^{\prime} ( z )\)

\[\psi _ {n} = N _ {n} e^{- z / 2} z^{b / 2} \mathcal {L} _ {n}^{b} ( z ) \label{83}\]

dónde\(N_{n}=[\alpha \cdot b \cdot n ! / \Gamma(k-n)]^{1 / 2}\),\(z=k \exp [-\alpha q], b=k-2 n-1\), y\(k=4 D_{e} / \hbar \omega_{0}\). Estas expresiones y las de los elementos matriciales en\(q, q^{2}, \mathrm{e}^{-\alpha q}, \text {and} q \mathrm{e}^{-\alpha q}\) han sido dadas por Vasan y Cross.

Momento angular

Operadores de momento angular

Para describir la rotación mecánica cuántica o el movimiento orbital, se tiene que cuantificar el momento angular. El operador de momento angular orbital total se define como

\[\hat{L}=\hat{r} \times \hat{p}=i \hbar(\hat{r} \times \nabla)\]

Tiene tres componentes\(\left(\hat{L}_{x}, \hat{L}_{y}, \hat{L}_{z}\right)\) que generan rotación alrededor del eje x, y o z, y cuya magnitud viene dada por

\(\hat{L}^{2}=\hat{L}_{x}^{2}+\hat{L}_{y}^{2}+\hat{L}_{z}^{2}\). Los operadores de momento angular siguen las relaciones de conmutación

\[\left[ H , L _ {z} \right] = 0 \label{85A}\]

\[\left[ H , L^{2} \right] = 0 \label{85B}\]

\[\left[ L _ {x} , L _ {y} \right] = i \hbar L _ {z} \label{86}\]

(En la Ecuación\ ref {86} los\(z\) índices\(x\)\(y\),, pueden permutarse cíclicamente.) Hay una base propia común a\(H\) y\(L^2\) y una de las\(L_i\), que tomamos para ser\(L_z\). Los valores propios para el operador de momento angular orbital L y la proyección z del momento angular Lz son

\[L^{2} | \ell m \rangle = \hbar^{2} \ell ( \ell + 1 ) | \ell m \rangle \quad \ell = 0,1,2 \ldots \label{87}\]

\[L _ {z} | \ell m \rangle = \hbar m | \ell m \rangle \quad m = 0 , \pm 1 , \pm 2 \ldots \pm \ell \label{88}\]

donde los estados propios\(| \ell m \rangle\) están etiquetados por el número cuántico de momento angular orbital\(\ell\), y el número cuántico magnético,\(m\).

Similar a la estrategia utilizada para el oscilador armónico, también podemos definir operadores de subida y bajada para el momento angular total,

\[\hat {L} _ {\pm} = \hat {L} _ {i} \pm \mathrm {i} \hat {L} _ {y} \label{89}\]

que siguen las relaciones de conmutación\(\left[ \hat {L}^{2} , \hat {L} _ {\pm} \right] = 0\) y\(\left[ \hat {L} _ {z} , \hat {L} _ {\pm} \right] = \pm \hbar \hat {L} _ {\pm}\), y satisfacen la ecuación del valor propio

\[\hat {L} _ {\pm} | \ell m \rangle = A _ {\ell , m} | \ell m \rangle \label{90}\]

\[A _ {\ell , m} = \hbar [ \ell ( \ell + 1 ) - m ( m \pm 1 ) ]^{1 / 2}\]

Potencial esféricamente simétrico

Examinemos el papel del momento angular para el caso de una partícula que experimenta un potencial esféricamente simétrico V (r) como el átomo de hidrógeno, el oscilador armónico isotrópico 3D y las partículas o moléculas libres. Para una partícula con masa\(m_{R}\), el hamiltoniano es

\[\hat{H}=-\frac{\hbar^{2}}{2 m} \nabla^{2}+V(r) \label{91}\]

Escribir el operador de energía cinética en coordenadas esféricas,

\[-\frac{\hbar^{2}}{2 m} \nabla^{2}=-\frac{\hbar^{2}}{2 m}\left(\frac{1}{r^{2}} \frac{\partial}{\partial r} r^{2} \frac{\partial}{\partial r}-\frac{1}{r^{2}} L^{2}\right) \label{92}\]

donde el cuadrado del momento angular total es

\[L^{2}=-\frac{1}{\sin \theta}\left(\frac{1}{\sin \theta} \frac{\partial^{2}}{\partial \phi^{2}}+\frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta}\right) \label{93}\]

Observamos que esta representación separa la dependencia radial en el hamiltoniano de la parte angular. Por lo tanto, esperamos que la función de onda general pueda escribirse como un producto de una parte radial y una parte angular en la forma

\[\psi(r, \theta, \phi)=R(r) Y(\theta, \phi) \label{94}\]

Sustituyendo esto en el TISE, encontramos que resolvemos las funciones de onda orientacional y radial por separado. Considerando soluciones primero a la parte angular, observamos que el potencial es solo una función de r, y solo hay que considerar el momento angular. Esto lleva a las identidades en eqs. (\ ref {87}) y (\ ref {88}), y revela que las funciones de\(|\ell m\rangle\) onda proyectadas sobre coordenadas esféricas están representadas por los armónicos esféricos

\[Y_{\ell}^{m}(\theta, \phi)=N_{t m}^{Y} P_{\ell}^{|m|}(\cos \theta) \mathrm{e}^{i m \phi} \label{95}\]

\(P_{\ell}^{m}\)son los polinomios de Legendre asociados y el factor de normalización es

\[N_{(m}^{Y}=(-1)^{(m+\mid m) / 2} i^{\ell}\left[\frac{2 \ell+1}{4 \pi} \frac{(\ell-|m|) !}{(\ell+|m|) !}\right]^{1 / 2}\]

Los componentes angulares de la función de onda son comunes a todos los estados propios de potenciales esféricamente simétricos. En química, es común usar funciones de onda angulares reales en lugar de la forma compleja en eq. (\ ref {95}). Estas se construyen a partir de las combinaciones lineales\(Y_{\mathrm{n}, z} \pm Y_{\mathrm{n},-\ell}\).

Sustituyendo eq. (\ ref {92}) y eq. (\ ref {87}) en eq. (\ ref {91}) conduce a un nuevo hamiltoniano que se puede insertar en la ecuación de Schrödinger. Esto se puede resolver como un problema puramente radial para un valor dado de\(l\). Es conveniente definir la función de distribución radial\(\chi(r)=r R(r)\), que permite que el TISE se reescriba como

\[\left(-\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial r^{2}}+U(r, \ell)\right) \chi=E \chi \label{96}\]

U juega el papel de un potencial efectivo

\[U(r, \ell)=V(r)+\frac{\hbar^{2}}{2 m r^{2}} \ell(\ell+1) \label{97}\]

La ecuación (\ ref {96}) se conoce como la ecuación de onda radial. Parece el TISE para un problema unidimensional en r, donde podríamos resolver esta ecuación para cada valor de\(\ell\). Nota U tiene una barrera debido a la energía cinética centrífuga que escala como\(r^{-2} \text {for} \ell>0\).

Las funciones de onda definidas en la eq. (\ ref {94}) se normalizan de tal manera que

\[\int|\psi|^{2} d \Omega=1 \label{98}\]

donde

\[\int d \Omega \equiv \int_{0}^{\infty} r^{2} d r \int_{0}^{\pi} \sin \theta d \theta \int_{0}^{2 \pi} d \phi \label{99}\]

Si restringimos la integración a estar por encima de todos los ángulos, encontramos que la probabilidad de encontrar una partícula entre una distancia r y\(r+d r \text {is} P(r)=4 \pi r^{2}|R(r)|^{2}=4 \pi|\chi(r)|^{2}\).

A este punto el tratamiento del momento angular orbital es idéntico para cualquier potencial esféricamente simétrico. Ahora debemos considerar la forma específica del potencial; por ejemplo en el caso del oscilador armónico isotrópico,\(U(r)=1 / 2 \kappa r^{2}\). En el caso de una partícula libre, sustituimos\(V(r)=0 \text {in eq.}(\ref{97})\) y encontramos que las soluciones radiales pueden escribirse en términos de funciones esféricas de Bessel,\(j_{\ell}\). Entonces las soluciones a la función de onda completa para la partícula libre se pueden escribir como

\[\Psi(r, \theta, \phi)=j_{\ell}(\mathrm{k} r) Y_{\ell}^{m}(\theta, \phi) \label{100}\]

donde el evector de ondas k se define como en la eq. (\ ref {46}).

Átomo de hidrógeno

Para un átomo similar a hidrógeno, un solo electrón de carga e interactúa con un núcleo de carga\(Ze\) bajo la influencia de un potencial de Coulomb

\[V_{H}(r)=-\frac{Z e^{2}}{4 \pi \epsilon_{0}} \frac{1}{r} \label{101}\]

Podemos simplificar la expresión definiendo unidades atómicas para distancia y energía. El radio de Bohr se define como

\[a_{0}=4 \pi \varepsilon_{0} \frac{\hbar^{2}}{m_{e} e^{2}}=5.2918 \times 10^{-11} \mathrm{~m} \label{102}\]

y el Hartree es

\[\mathcal{E}_{H}=\frac{1}{4 \pi \varepsilon_{0}} \frac{e^{2}}{a_{0}}=4.3598 \times 10^{-18} J=27.2 \mathrm{eV} \label{103}\]

Escrito en términos de unidades atómicas, podemos ver a partir de la eq. (\ ref {103}) que eq. (\ ref {101}) se convierte\(\left(V / \mathcal{E}_{H}\right)=-Z /\left(r / a_{0}\right)\). Así, la conversión establece efectivamente las variables SI\(m_{\mathrm{e}}=e=\left(4 \pi \varepsilon_{0}\right)^{-1}=\hbar = 1\). Entonces la ecuación de onda radial es

\[\frac{\partial^{2} \chi}{\partial r^{2}}+\left(\frac{2 Z}{r}-\frac{\ell(\ell+1)}{r^{2}}\right) \chi=2 E \chi \label{104}\]

El potencial efectivo dentro de los paréntesis en la eq. (\ ref {104}) se muestra en la Figura 5 para variar\(\ell\). Las soluciones a la función de onda radial para el átomo de hidrógeno toman la forma

\[R_{n \ell}(r)=N_{n \ell}^{R} \rho^{\ell} \mathcal{L}_{n+\ell}^{2 \ell+1}(\rho) e^{-\rho / 2} \label{105}\]

donde el radio reducido\(\rho=2 r / n a_{0} \text {and} \mathcal{L}_{k}^{\alpha}(z)\) son los polinomios asociados de Laguerre. El número cuántico primario toma valores enteros\(n=1,2,3 \ldots, \text {and} \ell\) está restringido de tal manera que\(\ell= 0,1,2 \ldots n-1\). El factor de normalización radial en eq. (\ ref {105}) es

\[N_{n \ell}^{R}=-\frac{2}{n^{3} a_{0}^{3 / 2}}\left[\frac{(\mathrm{n}-\ell-1) !}{[(n+1) !]^{3}}\right]^{1 / 2} \label{106}\]

Los valores propios de la energía son

\[E_{n}=-\frac{Z^{2}}{2 n^{2}} \mathcal{E}_{H} \label{107}\]

Figura 5. El potencial efectivo radial,\(U_{e f f}(\rho)\)

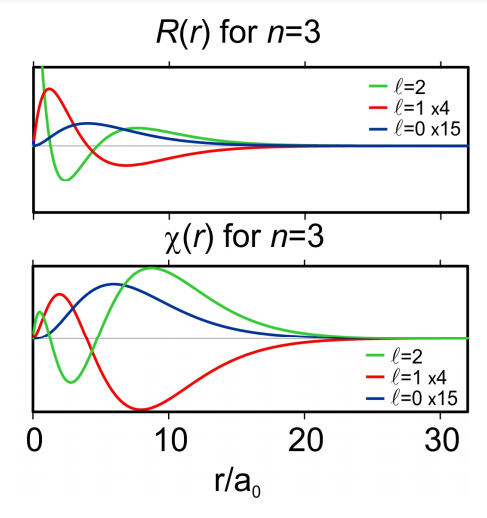
Figura 6. Densidad de probabilidad radial R y función de distribución radial\(\chi=r R\).

Espín de electrones

Al describir las funciones de onda electrónicas, el espín electrónico también da como resultado una contribución al momento angular total, y resulta en una contribución de espín a la función de onda. El momento angular de espín electrónico S y su proyección z se cuantifican como

\[S^{2}\left|s m_{s}\right\rangle=\hbar^{2} s(s+1)\left|s m_{s}\right\rangle \quad s=0,1 / 2,1,3 / 2,2 \ldots \label{108}\]

\[S_{z}\left|s m_{s}\right\rangle=\hbar m_{s}\left|s m_{s}\right\rangle \quad m_{s}=-s,-s+1, \ldots, s \label{109}\]

donde los estados propios de espín electrónico\(\left|s m_{s}\right\rangle\) están etiquetados por el número cuántico de momento angular de espín electrónico s y el número cuántico magnético de espín\(m s\). El número de valores de\(S_{z}\) es\(2 s+1\) y se conoce como la multiplicidad de espín. Como fermiones, los electrones tienen espín medio entero, y cada electrón no apareado contribuye\(1 / 2\) al número cuántico de espín de electrones s. Un solo electrón no apareado tiene configuraciones\(s=1 / 2, \text {for which} m_{s}=\pm 1 / 2\) correspondientes a espin-up y spin-down. Para los sistemas de múltiples electrones, el espín se calcula como la suma vectorial de espines, esencialmente\(1 / 2\) multiplicada por el número de electrones desapareados.

El momento angular total resultante para un electrón es\(J=L+S\). J le ha asociado el número cuántico de momento angular total\(j\), que adquiere valores de\(j=|\ell-s|,|\ell-s|+1, \ldots \ell+s\). La naturaleza aditiva de las contribuciones orbitales y de espín al momento angular conduce a una función de onda electrónica total que es un producto de las funciones espaciales y de ondas de espín.

\[\Psi_{\text {tot}}=\Psi(r, \theta, \phi)\left|s m_{s}\right\rangle \label{110}\]

Así, el estado de un electrón puede especificarse mediante cuatro números cuánticos\(\Psi_{t o t}=\left|n \ell m_{\ell} m_{s}\right\rangle\).

Rotor Rígido

En el caso de una molécula anisotrópica que gira libremente, el momento angular total J se obtiene de la suma del momento angular orbital L y el momento angular de giro S para los constituyentes moleculares:\(J=L+S, \text {where} L=\sum_{i} L_{i} \text {and} S=\sum_{i} S_{i}\). El caso del rotor rígido se refiere al modelo mínimo para los estados cuánticos rotacionales de un objeto que gira libremente que tiene simetría cilíndrica y sin giro magnético. Entonces, el hamiltoniano viene dado por la energía cinética rotacional

\[H_{r o t}=\frac{\hat{J}^{2}}{2 I} \label{111}\]

I es el momento de inercia sobre el eje principal de rotación. Las funciones propias de este hamiltoniano son armónicos esféricos\(Y_{J, M}(\theta, \phi)\)

\ [\ begin {array} {ll}
\ hat {J} ^ {2}\ izquierda|y_ {J, M}\ derecha\ rangle=\ hbar^ {2} J (J+1)\ izquierda|y_ {J, M}\ derecha\ rangle & J=0,1,2\ ldots\\
\ sombrero {J} _ _ {z}\ izquierda|y_ {J, M}\ derecha\ rangle=M\ hbar\ izquierda|y_ {J, M}\ derecha\ rangle & M=-J, -J+1,\ ldots, J
\ end {array}\ label {112}\]

J es el número cuántico rotacional. M es su proyección sobre el eje z. Los valores propios de energía para\(H_{\text {rot}}\) son

\[E_{J, M}=\bar{B} J(J+1) \label{113}\]

donde la constante de rotación es

\[\bar{B}=\frac{\hbar^{2}}{2 I} \label{114}\]

Más comúnmente,\(\bar{B}\) se da en unidades de\(c m^{-1} \text {using} \bar{B}=h / 8 \pi^{2} I c\).