3.3: Transiciones inducidas por el potencial dependiente del tiempo

Para muchos problemas dependientes del tiempo, sobre todo en espectroscopia, a menudo podemos dividir el problema para que el hamiltoniano dependiente del tiempo contenga una parte independiente del tiempo\(H_0\) que podamos describir exactamente, y un potencial dependiente del tiempo\(V(t)\)

\[H = H _ {0} + V (t) \label{2.45}\]

Los restantes grados de libertad son descartados, y luego sólo entran en el sentido de que dan lugar al potencial de interacción con\(H_0\). Esto es efectivo si tienes razones para creer que el hamiltoniano externo puede ser tratado clásicamente, o si la influencia de\(H_0\) en los otros grados de libertad es insignificante. A partir de la Ecuación\ ref {2.45}, existe un enfoque directo para describir la función de onda que evoluciona en el tiempo para el sistema en términos de los autoestados y los valores propios de energía de\(H_0\).

Para comenzar, conocemos el conjunto completo de autoestados y valores propios para el sistema hamiltoniano

\[H _ {0} | n \rangle = E _ {n} | n \rangle \label{2.46}\]

El estado del sistema puede entonces expresarse como una superposición de estos autoestados:

\[| \psi (t) \rangle = \sum _ {n} c _ {n} (t) | n \rangle \label{2.47}\]

El TDSE se puede utilizar para encontrar una ecuación de movimiento para los coeficientes de estado propio

\[c _ {k} (t) = \langle k | \psi (t) \rangle \label{2.48}\]

Empezando con

\[\frac {\partial | \psi \rangle} {\partial t} = \frac {- i} {\hbar} H | \psi \rangle \label{2.49}\]

\[\frac {\partial c _ {k} (t)} {\partial t} = - \frac {i} {\hbar} \langle k | H | \psi (t) \rangle \label{2.50}\]

y de Ecuación\ ref {2.47}

\[\frac {\partial c _ {k} (t)} {\partial t} = - \frac {i} {\hbar} \sum _ {n} \langle k | H | n \rangle c _ {n} (t) \label{2.51}\]

Ya vemos que la evolución temporal equivale a resolver un conjunto de ecuaciones diferenciales ordinarias lineales acopladas. Se trata de ecuaciones de velocidad con constantes de velocidad complejas, que describen la alimentación de un estado a otro. Ecuación sustitutiva\ ref {2.45} tenemos:

\[\left.\begin{aligned} \frac {\partial c _ {k} (t)} {\partial t} & = - \frac {i} {\hbar} \sum _ {n} \left\langle k \left| \left( H _ {0} + V (t) \right) \right| n \right\rangle c _ {n} (t) \\ & = - \frac {i} {\hbar} \sum _ {n} \left[ E _ {n} \delta _ {k n} + V _ {k n} (t) \right] c _ {n} (t) \end{aligned} \right. \label{2.52}\]

o\(\frac {\partial c _ {k} (t)} {\partial t} + \frac {i} {\hbar} E _ {k} c _ {k} (t) = - \frac {i} {\hbar} \sum _ {n} V _ {k n} (t) c _ {n} (t) \label{2.53}\)

A continuación, definimos y sustituimos

\[c _ {m} (t) = e^{- i E _ {m} t / h} b _ {m} (t) \label{2.54}\]

lo que implica una definición para la función de onda como

\[| \psi (t) \rangle = \sum _ {n} b _ {n} (t) e^{- i E _ {n} t / h} | n \rangle \label{2.55}\]

Esto define una amplitud compleja ligeramente diferente, que nos permite simplificar las cosas considerablemente. Observe que

\[\left| b _ {k} (t) \right|^{2} = \left| c _ {k} (t) \right|^{2}.\]

También,\(b _ {k} ( 0 ) = c _ {k} ( 0 )\). En la práctica lo que estamos haciendo es sacar la parte “trivial” de la evolución del tiempo, el factor de fase de evolución temporal, que típicamente oscila mucho más rápido que los cambios en la amplitud de\(b\) o\(c\).

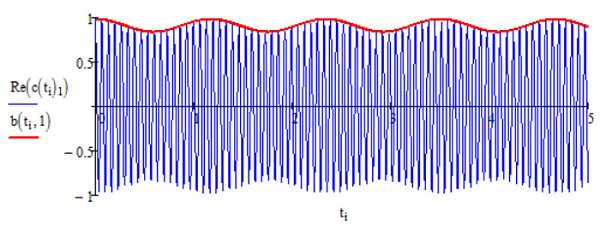
Volveremos a esta estrategia en la que discutimos el panorama de la interacción.

Ahora la ecuación\ ref {2.53} se convierte

\[e^{- i E _ {t} t / h} \frac {\partial b _ {k}} {\partial t} = - \frac {i} {\hbar} \sum _ {n} V _ {k n} (t) e^{- i E _ {n} t / h} b _ {n} (t) \label{2.56}\]

o\(i \hbar \frac {\partial b _ {k}} {\partial t} = \sum _ {n} V _ {k n} (t) e^{- i \omega _ {n k} t} b _ {n} (t) \label{2.57}\)

Esta ecuación es una solución exacta. Se trata de un conjunto de ecuaciones diferenciales acopladas que describen cómo la amplitud de probabilidad se mueve a través de estados propios debido a un potencial dependiente del tiempo. Excepto en casos simples, estas ecuaciones no pueden resolverse analíticamente, pero a menudo es sencillo de integrar numéricamente.

¿Cuándo podemos usar el enfoque aquí descrito? Considera dividir el hamiltoniano completo en dos componentes, uno que queremos estudiar\(H_0\) y los restantes grados de libertad\(H_1\). Para cada parte, tenemos conocimiento de los autoestados completos y valores propios del hamiltoniano:\(H _ {i} | \psi _ {i , n} \rangle = E _ {i , n} | \psi _ {i , n} \rangle\). Estos subsistemas interactuarán entre sí a través de\(H_{int}\). Si tenemos cuidado de particionar esto de tal manera que HIP sea pequeño comparado\(H_0\) y\(H_1\), entonces debería ser posible describir correctamente el estado del sistema completo como estados de producto en los subsistemas:\(| \psi \rangle = | \psi _ {0} \psi _ {1} \rangle\). Además, podemos escribir una ecuación de Schrödinger dependiente del tiempo para el movimiento de cada subsistema como:

\[i \hbar \frac {\partial | \psi _ {1} \rangle} {\partial t} = H _ {1} | \psi _ {1} \rangle \label{2.58}\]

Dentro de estos supuestos, podemos escribir la ecuación completa de Schrödinger dependiente del tiempo en términos de los dos subestados:

\[i \hbar | \psi _ {0} \rangle \frac {\partial | \psi _ {1} \rangle} {\partial t} + i \hbar | \psi _ {1} \rangle \frac {\partial | \psi _ {0} \rangle} {\partial t} = | \psi _ {0} \rangle H _ {1} | \psi _ {1} \rangle + | \psi _ {1} \rangle H _ {0} | \psi _ {0} \rangle + H _ {\mathrm {int}} | \psi _ {0} \rangle | \psi _ {1} \rangle \label{2.59}\]

Luego a la izquierda operando por\(\langle \psi _ {1} |\) y haciendo uso de la Ecuación\ ref {2.58}, podemos escribir

\[i \hbar \frac {\partial | \psi _ {0} \rangle} {\partial t} = \left[ H _ {0} + \left\langle \psi _ {1} \left| H _ {\mathrm {int}} \right| \psi _ {1} \right\rangle \right] | \psi _ {0} \rangle \label{2.60}\]

Esto es equivalente al TDSE para un hamiltoniano de forma (Ecuación\ ref {2.45}) donde la interacción externa\(V (t) = \left\langle \psi _ {1} \left| H _ {\mathrm {int}} (t) \right| \psi _ {1} \right\rangle\) proviene de integrar la interacción 1-2 sobre el subespacio de\(| \psi _ {1} \rangle\). Entonces esto representa un método de campo medio dependiente del tiempo.

Lecturas

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; p. 308.
2. Merzbacher, E., Mecánica Cuántica. 3a ed.; Wiley: Nueva York, 1998; Ch. 14.
3. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Sec. 2.3.
4. Sakurai, J. J., Mecánica Cuántica Moderna, Edición Revisada. Addison-Wesley: Reading, MA, 1994; Ch. 2.