3.4: Conducción resonante de un sistema de dos niveles

Vamos a describir lo que sucede cuando conduces un sistema de dos niveles con un potencial oscilante.

\[V (t) = V \cos \omega t \label{2.61}\]

\[V _ {k \ell} (t) = V _ {k \ell} \cos \omega t \label{2.62}\]

Tenga en cuenta que esta es la forma que esperaría de un campo electromagnético que interactúa con partículas cargadas, es decir, transiciones dipolares. En un sentido sencillo, el campo eléctrico es\(\overline {E} (t) = \overline {E} _ {0} \cos \omega t\) y el potencial de interacción puede escribirse como\(V = - \overline {E} \cdot \overline {\mu},\) donde\(\overline {\mu}\) representa al operador dipolo.

Más adelante veremos la forma de esta interacción con más detenimiento. Ahora acoplamos dos estados\(| a \rangle\) y\(| b \rangle\) con el campo oscilante. Aquí se ordena la energía de los estados para que\(\varepsilon _ {b} > \varepsilon _ {a}\). Preguntemos si el sistema inicia en\(| a \rangle\) ¿cuál es la probabilidad de encontrarlo en\(| a \rangle\) el momento\(t\)?

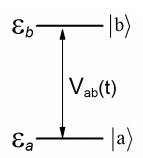
El sistema de ecuaciones diferenciales que describen este problema es:

\[\begin{align} i \hbar \frac {\partial} {\partial t} b _ {k} (t) & = \sum _ {n = a , b} b _ {n} (t) V _ {k n} (t) e^{- i \omega _ {n k} t} \\[4pt] & = \sum _ {n = a , b} b _ {n} (t) V _ {k n} e^{- i \omega _ {n k} t} \cdot \frac {1} {2} \left( e^{- i \omega t} + e^{i \omega t} \right) \label{2.63} \end{align}\]

Donde\(\cos \omega t\) en escrito su forma compleja. Escribiendo esto explícitamente

\[i \hbar \dot {b} _ {b} = \frac {1} {2} b _ {a} V _ {b a} \left[ e^{i \left( \omega _ {b a} - \omega \right) t} + e^{i \left( \omega _ {b a} + \omega \right) t} \right] + \frac {1} {2} b _ {b} V _ {b b} \left[ e^{i \omega t} + e^{- i \omega t} \right]\]

\[i \hbar \dot {b} _ {a} = \frac {1} {2} b _ {a} V _ {a a} \left[ e^{i \omega t} + e^{- i \omega t} \right] + \frac {1} {2} b _ {b} V _ {a b} \left[ e^{i \left( \omega _ {a b} - \omega \right) t} + e^{i \left( \omega _ {a b} + \omega \right) t} \right]\]

o alternadamente cambiar el último término:

\[i \hbar \dot {b} _ {a} = \frac {1} {2} b _ {a} V _ {a a} \left[ e^{i \omega t} + e^{- i \omega t} \right] + \frac {1} {2} b _ {b} V _ {a b} \left[ e^{- i \left( \omega _ {b a} + \omega \right) t} + e^{- i \left( \omega _ {b a} - \omega \right) t} \right]\]

Aquí las expresiones se han escrito en términos de la frecuencia\(\omega_{ba}\). Dos de estos términos se dejan caer, ya que (para nuestro caso) los elementos de la matriz diagonal\(V_{ii} =0\). También hacemos la aproximación secular (o aproximación de onda giratoria) en la que se dejan caer los términos no resonantes. Cuando\(\omega _ {b a} \approx \omega\), términos como\(e^{\pm i \omega t}\) u\(e^{i \left( \omega _ {b a} + \omega \right) t}\) oscilan muy rápidamente (relativo a\(\left| V _ {b a} \right|^{- 1}\)) y así no contribuyen mucho al cambio de\(c_n\). (Recuerda, tomamos las frecuencias\(\omega_{b a}\) y\(\omega\) para ser positivos). Entonces ahora tenemos:

\[\dot {b} _ {b} = \frac {- i} {2 \hbar} b _ {a} V _ {b a} e^{i \left( \omega _ {b a} - \omega \right) t} \label{2.66}\]

\[\dot {b} _ {a} = \frac {- i} {2 \hbar} b _ {b} V _ {a b} e^{- i \left( \omega _ {b a} - \omega \right) t} \label{2.67}\]

Obsérvese que los coeficientes oscilan a la misma frecuencia pero desplazados de fase entre sí. Ahora bien, si diferenciamos Ecuación\ ref {2.66}:

\[\ddot {b} _ {b} = \frac {- i} {2 \hbar} \left[ \dot {b} _ {a} V _ {b a} e^{i \left( \omega _ {b a} - \omega \right) t} + i \left( \omega _ {b a} - \omega \right) b _ {a} V _ {b a} e^{i \left( \omega _ {b a} - \omega \right) t} \right] \label{2.68}\]

Reescribir la ecuación\ ref {2.66}:

\[b _ {a} = \frac {2 i \hbar} {V _ {b a}} \dot {b} _ {b} e^{- i \left( \omega _ {b a} - \omega \right) t} \label{2.69}\]

y sustituimos las Ecuaciones\ ref {2.69} y\ ref {2.67} en la Ecuación\ ref {2.68}, obtenemos la ecuación lineal de segundo orden para\(b_b\).

\[\ddot {b} _ {b} - i \left( \omega _ {b a} - \omega \right) \dot {b} _ {b} + \frac {\left| V _ {b a} \right|^{2}} {4 \hbar^{2}} b _ {b} = 0 \label{2.70}\]

Esta es solo la ecuación diferencial de segundo orden para un oscilador armónico amortiguado:

\[a \ddot {x} + b \dot {x} + c x = 0 \label{2.71}\]

\[x = e^{- ( b / 2 a ) t} ( A \cos \mu t + B \sin \mu t ) \label{2.72}\]

con

\[\mu = \frac {1} {2 a} \sqrt {4 a c - b^{2}}\]

Con un poco más de manipulación, y recordando las condiciones iniciales\(b_j(0)=0\) y\(b_{\ell} (0) =1\), encontramos

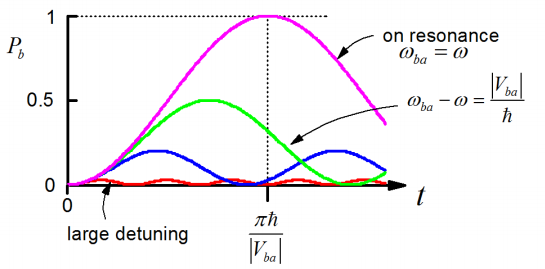
\[P _ {b} (t) = \left| b _ {b} (t) \right|^{2} = \frac {\left| V _ {b a} \right|^{2}} {\left| V _ {b a} \right|^{2} + \hbar^{2} \left( \omega _ {b a} - \omega \right)^{2}} \sin^{2} \Omega _ {R} t \label{2.73}\]

Donde la Frecuencia Rabi

\[\Omega _ {R} = \frac {1} {2 \hbar} \sqrt {\left| V _ {b a} \right|^{2} + \hbar^{2} \left( \omega _ {b a} - \omega \right)^{2}} \label{2.74}\]

También,

\[P _ {a} = 1 - P _ {b} \label{2.75}\]

La amplitud oscila de un lado a otro entre los dos estados a una frecuencia dictada por el acoplamiento entre ellos. [Nota un resultado al que volveremos más adelante: los campos eléctricos se acogen a estados cuánticos, ¡creando coherencias!]

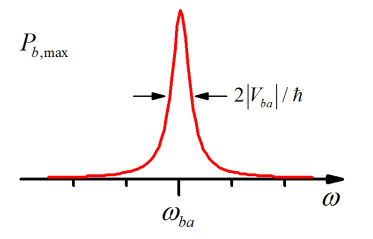
Una observación importante es la importancia de la resonancia entre el potencial impulsor y la división de energía entre estados. Para obtener la transferencia de densidad de probabilidad se necesita que el campo de conducción esté a la misma frecuencia que la división de energía. En resonancia, siempre conduces la amplitud de probabilidad por completo de un estado a otro.

La eficiencia de conducir entre\(| a \rangle\) y\(|b \rangle\) estados disminuye con la desintonización. Aquí trazando el valor máximo de\(P_b\) como una función de la frecuencia: