3.6: Imagen de interacción

El cuadro de interacción es una representación híbrida que es útil para resolver problemas con hamiltonianos dependientes del tiempo en los que podemos particionar el hamiltoniano como

\[H (t) = H_0 + V (t) \label{2.93}\]

\(H_0\)es un hamiltoniano por los grados de libertad que nos interesan, que tratamos exactamente, y puede ser (aunque para nosotros normalmente no lo será) una función del tiempo. \(V(t)\)es un potencial dependiente del tiempo que puede ser complicado. En el cuadro de interacción, trataremos cada parte del hamiltoniano en una representación diferente. Utilizaremos los autoestados de\(H_0\) como conjunto de bases para describir la dinámica inducida por\(V(t)\), asumiendo que\(V(t)\) es lo suficientemente pequeña como para que los autoestados de\(H_0\) sean una base útil. Si no\(H_0\) es una función del tiempo, entonces hay una simple dependencia del tiempo a esta parte del hamiltoniano que tal vez podamos dar cuenta fácilmente. Al poner\(V\) a cero, podemos ver que la evolución temporal de la parte exacta del hamiltoniano\(H_0\) es descrita por

\[\frac {\partial} {\partial t} U_0 \left( t , t_0 \right) = - \frac {i} {\hbar} H_0 (t) U_0 \left( t , t_0 \right) \label{2.94}\]

donde,

\[U_0 \left( t , t_0 \right) = \exp _ {+} \left[ - \frac {i} {\hbar} \int _ {t_0}^{t} d \tau H_0 (t) \right] \label{2.95}\]

o, para un tiempo independiente\(H_0\),

\[U_0 \left( t , t_0 \right) = e^{- i H_0 \left( t - t_0 \right) / \hbar} \label{2.96}\]

Definimos una función de onda en la imagen de interacción\(| \psi _ {I} \rangle\) en términos de la función de onda Schrödinger a través de:

\[| \psi _ {S} (t) \rangle \equiv U_0 \left( t , t_0 \right) | \psi _ {I} (t) \rangle \label{2.97}\]

o

\[| \psi _ {I} \rangle = U_0^{\dagger} | \psi _ {S} \rangle \label{2.98}\]

Efectivamente, la representación de interacción define las funciones de onda de tal manera que\(e^{- i H_0 t / h}\) se elimina la fase acumulada bajo. Para pequeños\(V\), estas son típicamente oscilaciones de alta frecuencia en relación con los cambios de amplitud más lentos inducidos por\(V\).

Ahora necesitamos una ecuación de movimiento que describa la evolución temporal de las funciones de onda de imagen de interacción. Comenzamos sustituyendo la Ecuación\ ref {2.97} en el TDSE:

\[ \begin{align} | \psi _ {S} (t) \rangle & = U_0 \left( t , t_0 \right) | \psi _ {1} (t) \rangle \\[4pt] & = U_0 \left( t , t_0 \right) U _ {I} \left( t , t_0 \right) | \psi _ {I} \left( t_0 \right) \rangle \\[4pt] & = U_0 \left( t , t_0 \right) U _ {I} \left( t , t_0 \right) | \psi _ {S} \left( t_0 \right) \rangle \\[4pt] \therefore \quad U & \left( t , t_0 \right) = U_0 \left( t , t_0 \right) U _ {I} \left( t , t_0 \right) \end{align} \]

\[\therefore \quad i \hbar \frac {\partial | \psi _ {I} \rangle} {\partial t} = V_I | \psi _ {I} \rangle \label{2.101}\]

donde

\[V_I (t) = U_0^{\dagger} \left( t , t_0 \right) V (t) U_0 \left( t , t_0 \right) \label{2.102}\]

\(| \psi _ {I} \rangle\)satisface la ecuación de Schrödinger con un nuevo hamiltoniano en la ecuación\ ref {2.102}: la imagen de interacción hamiltoniana,\(V_I(t)\). Hemos realizado una transformación unitaria de\(V(t)\) en el marco de referencia de\(H_0\), utilizando\(U_0\). Nota: Elementos de matriz en

\[V_I = \left\langle k \left| V_I \right| l \right\rangle = e^{- i \omega _ {l k} t} V _ {k l}\]

donde\(k\) y\(l\) son estados propios de\(H_0\). Ahora podemos definir un operador de evolución temporal en la imagen de interacción:

\[| \psi _ {I} (t) \rangle = U _ {I} \left( t , t_0 \right) | \psi _ {I} \left( t_0 \right) \rangle \label{2.103}\]

donde

\[U _ {I} \left( t , t_0 \right) = \exp _ {+} \left[ \frac {- i} {\hbar} \int _ {t_0}^{t} d \tau V_I ( \tau ) \right] \label{2.104}\]

Ahora vemos que

\ [\ begin {alineado}
\ izquierda|\ psi_ {S} (t)\ derecha\ rangle &=U_ {0}\ izquierda (t, t_ {0}\ derecha)\ izquierda|\ psi_ {I} (t)\ derecha\ rangle\\ [4pt]
&=U_ {0}\ izquierda (t, t_ {0}\ derecha) U_ {I}\ izquierda (t, t_ {0}\ derecha)\ izquierda|\ psi_ {I}\ izquierda (t_ {0}\ derecha)\ derecha\ rangle\\ [4pt]
&=U_ {0}\ izquierda (t, t_ {0}\ derecha) U_ { I}\ izquierda (t, t_ {0}\ derecha)\ izquierda|\ psi_ {S}\ izquierda (t_ {0}\ derecha)\ derecha\ rangle
\ final {alineado}\]

\[\therefore U\left(t, t_{0}\right)=U_{0}\left(t, t_{0}\right) U_{I}\left(t, t_{0}\right)\label{2.106}\]

Además, se puede escribir la evolución temporal de la función de onda conjugada en la imagen de interacción

\[U^{\dagger} \left( t , t_0 \right) = U _ {I}^{\dagger} \left( t , t_0 \right) U_0^{\dagger} \left( t , t_0 \right) = \exp _ {-} \left[ \frac {i} {\hbar} \int _ {t_0}^{t} d \tau V_I ( \tau ) \right] \exp _ {-} \left[ \frac {i} {\hbar} \int _ {t_0}^{t} d \tau H_0 ( \tau ) \right] \label{2.107}\]

Para las dos últimas expresiones, el orden de estos operadores ciertamente importa. Entonces, ¿qué cambia sobre la propagación del tiempo en la representación de interacción? Empecemos por escribir el exponencial ordenado por tiempo para\(U\) en la Ecuación\ ref {2.106} usando la Ecuación\ ref {2.104}:

\[ \begin{align} U \left( t , t_0 \right) &= U_0 \left( t , t_0 \right) + \left( \frac {- i} {\hbar} \right) \int _ {t_0}^{t} d \tau U_0 ( t , \tau ) V ( \tau ) U_0 \left( \tau , t_0 \right) + \cdots \\[4pt] &= U_0 \left( t , t_0 \right) + \sum _ {n = 1}^{\infty} \left( \frac {- i} {\hbar} \right)^{n} \int _ {t_0}^{t} d \tau _ {n} \int _ {t_0}^{\tau _ {n}} d \tau _ {n - 1} \cdots \int _ {t_0}^{\tau _ {2}} d \tau _ {1} U_0 \left( t , \tau _ {n} \right) V \left( \tau _ {n} \right) U_0 \left( \tau _ {n} , \tau _ {n - 1} \right) \ldots \times U_0 \left( \tau _ {2} , \tau _ {1} \right) V \left( \tau _ {1} \right) U_0 \left( \tau _ {1} , t_0 \right) \label{2.108} \end{align}\]

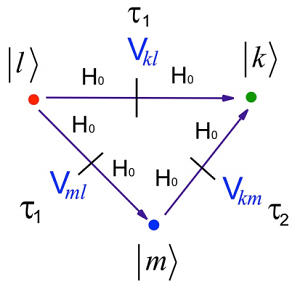
Aquí he usado la propiedad de composición de\(U \left( t , t_0 \right)\). Se aplica el mismo orden de tiempo positivo. Tenga en cuenta que las interacciones no\(V(\tau_i)\) están en la representación de interacción aquí. Más bien usamos la definición en Ecuación\ ref {2.102} y recogimos términos. Ahora considere cómo\(U\) describe la dependencia del tiempo si\(I\) inicia el sistema en un estado propio de\(H_0\),\(| l \rangle\) y observar la amplitud en un estado propio objetivo\(| k \rangle\). El sistema evoluciona en estados propios de\(H_0\) durante los diferentes periodos de tiempo, con las interacciones dependientes del tiempo\(V\) impulsando las transiciones entre estos estados. El término de primer orden describe transiciones directas entre\(l\) e\(k\) inducidas por\(V\), integradas durante el período de tiempo completo. Antes se adquiere la fase de interacción como\(e^{- i E _ {\ell} \left( \tau - t_0 \right) / \hbar}\), mientras que después de la fase de interacción se adquiere como\(e^{- i E _ {\ell} ( t - \tau ) / \hbar}\). Términos de orden superior en las cuentas exponenciales ordenadas por tiempo para todas las vías intermedias posibles.

Ahora sabemos cómo las funciones de onda de imagen de interacción evolucionan en el tiempo. ¿Qué pasa con los operadores? En primer lugar, al examinar el valor de expectativa de un operador vemos

\[\left.\begin{aligned} \langle \hat {A} (t) \rangle & = \langle \psi (t) | \hat {A} | \psi (t) \rangle \\[4pt] & = \left\langle \psi \left( t_0 \right) \left| U^{\dagger} \left( t , t_0 \right) \hat {A} U \left( t , t_0 \right) \right| \psi \left( t_0 \right) \right\rangle \\[4pt] & = \left\langle \psi \left( t_0 \right) \left| U _ {I}^{\dagger} U_0^{\dagger} \hat {A} U_0 U _ {I} \right| \psi \left( t_0 \right) \right\rangle \\[4pt] & = \left\langle \psi _ {L} (t) \left| \hat {A} _ {L} \right| \psi _ {L} (t) \right\rangle \end{aligned} \right. \label{2.109}\]

donde

\[A _ {I} \equiv U_0^{\dagger} A _ {S} U_0 \label{2.110}\]

Entonces los operadores en la imagen de interacción también evolucionan en el tiempo, pero bajo\(H_0\). Esto se puede expresar como una ecuación de Heisenberg diferenciando

\[\frac {\partial} {\partial t} \hat {A} _ {I} = \frac {i} {\hbar} \left[ H_0 , \hat {A} _ {I} \right] \label{2.111}\]

También, sabemos

\[\frac {\partial} {\partial t} | \psi _ {I} \rangle = \frac {- i} {\hbar} V_I (t) | \psi _ {I} \rangle \label{2.112}\]

Observe que la representación de interacción es una partición entre las representaciones de Schrödinger y Heisenberg. Las funciones de onda evolucionan bajo VI, mientras que los operadores evolucionan bajo

\[\text {For} H_0 = 0 , V (t) = H \quad \Rightarrow \quad \frac {\partial \hat {A}} {\partial t} = 0 ; \quad \frac {\partial} {\partial t} | \psi _ {S} \rangle = \frac {- i} {\hbar} H | \psi _ {S} \rangle \text{For Schrödinger} \]

\[\text {For} H_0 = H , V (t) = 0 \Rightarrow \frac {\partial \hat {A}} {\partial t} = \frac {i} {\hbar} [ H , \hat {A} ] ; \quad \frac {\partial \psi} {\partial t} = 0 \text{For Heisenberg} \label{2.113}\]

La relación entre UI y bn

Anteriormente describimos cómo los problemas dependientes del tiempo con los hamiltonianos de la forma\(H = H_0 + V (t)\) podrían resolverse en términos de las amplitudes que evolucionan en el tiempo en los propios estados de\(H_0\). Podemos describir el estado del sistema como una superposición

\[| \psi (t) \rangle = \sum _ {n} c _ {n} (t) | n \rangle \label{2.114}\]

donde los coeficientes de expansión\(c _ {k} (t)\) están dados por

\[\left.\begin{aligned} c _ {k} (t) & = \langle k | \psi (t) \rangle = \left\langle k \left| U \left( t , t_0 \right) \right| \psi \left( t_0 \right) \right\rangle \\[4pt] & = \left\langle k \left| U_0 U _ {I} \right| \psi \left( t_0 \right) \right\rangle \\[4pt] & = e^{- i E _ {k} t / \hbar} \left\langle k \left| U _ {I} \right| \psi \left( t_0 \right) \right\rangle \end{aligned} \right. \label{2.115}\]

Ahora, comparar las ecuaciones\ ref {2.115} y\ ref {2.54} nos permite reconocer que nuestros coeficientes de expansión modificados anteriormente\(b_n\) eran coeficientes de expansión para funciones de onda de imagen de interacción

\[b _ {k} (t) = \langle k | \psi _ {I} (t) \rangle = \left\langle k \left| U _ {I} \right| \psi \left( t_0 \right) \right\rangle \label{2.116}\]

Lecturas

1. Mukamel, S., Principios de Espectroscopia Óptica No Lineal. Oxford University Press: Nueva York, 1995.
2. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Cap. 4.