3.7: Teoría de la perturbación dependiente del tiempo

La teoría de perturbación se refiere a calcular la dependencia del tiempo de un sistema truncando la expansión del operador de tiempo-evolución de imagen de interacción después de un cierto término. En la práctica, truncar el propagador de tiempo completo no\(U\) es efectivo, y solo funciona bien por tiempos cortos en comparación con la inversa de la división de energía entre estados acoplados de su hamiltoniano. El cuadro de interacción se aplica a los hamiltonianos que pueden ser lanzados como

\[H=H_o + V(t)\]

y nos permite enfocarnos en la influencia del acoplamiento. Entonces podemos tratar la evolución del tiempo bajo\(H_o\) exactamente, pero truncar la influencia de\(V(t)\). Esto funciona bien para las perturbaciones débiles. Veamos más de cerca esto.

Conocemos los estados propios para\(H_o\):

\[H _ {0} | n \rangle = E _ {n} | n \rangle\]

y podemos calcular la evolución de la función de onda que resulta de\(V(t)\):

\[| \psi _ {I} (t) \rangle = \sum _ {n} b _ {n} (t) | n \rangle \label{2.117}\]

Para un estado dado\(k\), calculamos\(b_k(t)\) como:

\[b _ {k} = \left\langle k \left| U _ {I} \left( t , t _ {0} \right) \right| \psi \left( t _ {0} \right) \right\rangle \label{2.118}\]

donde

\[U _ {I} \left( t , t _ {0} \right) = \exp _ {+} \left[ \frac {- i} {\hbar} \int _ {t _ {0}}^{t} V _ {I} ( \tau ) d \tau \right ]\label{2.119}\]

Ahora podemos truncar la expansión después de algunos términos. Esto funciona bien para pequeños cambios en la amplitud de los estados cuánticos con pequeños elementos de la matriz de acoplamiento en relación con las divisiones de energía involucradas (\(\left| b _ {k} (t) \right| \approx \left| b _ {k} ( 0 ) \right| ; | V | \ll \left| E _ {k} - E _ {n} \right|\)). Como veremos, los resultados que obtenemos de la teoría de la perturbación son ampliamente utilizados para espectroscopía, dinámica de fase condensada y relajación. Tomemos el caso específico donde tenemos un sistema preparado en, y queremos saber la probabilidad de observar el sistema en el\(| k \rangle\) momento\(t\) debido a\(V(t)\):

\[P _ {k} (t) = \left| b _ {k} (t) \right|^{2}] \label{2.120}.\]

Ampliando

\[b _ {k} (t) = \langle k | \exp _ {+} \left[ - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau V _ {I} ( \tau ) \right] \ell \rangle\]

\[\left.\begin{aligned} b _ {k} (t) = \langle k | \ell \rangle & - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau \left\langle k \left| V _ {I} ( \tau ) \right| \ell \right\rangle \\ & + \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d \tau _ {2} \int _ {t _ {0}}^{\tau _ {2}} d \tau _ {1} \left\langle k \left| V _ {I} \left( \tau _ {2} \right) V _ {I} \left( \tau _ {1} \right) \right| \ell \right\rangle + \ldots \end{aligned} \right. \label{2.121}\]

Ahora, usando

\[\left\langle k \left| V _ {I} (t) \right| \ell \right\rangle = \left\langle k \left| U _ {0}^{\dagger} V (t) U _ {0} \right| \ell \right\rangle = e^{- i \omega _ {l k} t} V _ {k \ell} (t) \label{2.122}\]

obtenemos:

\[b _ {k} (t) = \delta _ {k \ell} - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau _ {1} e^{- i \omega _ {l k} \tau _ {1}} V _ {k \ell} \left( \tau _ {1} \right) "first-order” \label{2.123}\]

\[+ \sum _ {m} \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d \tau _ {2} \int _ {t _ {0}}^{\tau _ {2}} d \tau _ {1} e^{- i \omega _ {m k} \tau _ {2}} V _ {k n} \left( \tau _ {2} \right) e^{- i \omega _ {\ln t _ {1}}} V _ {m \ell} \left( \tau _ {1} \right) \label{2.124}\]

\[ + ...\]

El término de primer orden solo permite transiciones directas entre\(| \ell \rangle\) y\(| k \rangle\), según lo permita el elemento matriz en\(V\), mientras que el término de segundo orden da cuenta de las transiciones que ocurren a través de todos los estados intermedios posibles\(| m \rangle\). Para la teoría de la perturbación, la integral ordenada por el tiempo se trunca en el orden apropiado. Incluyendo solo la primera integral es la teoría de perturbación de primer orden. El orden de la teoría de perturbación que uno extendería un cálculo debe evaluarse inicialmente por el cual las vías permitidas entre\(| \ell \rangle\) y hay\(| k \rangle\) que dar cuenta y cuáles son permitidas por los elementos de la matriz.

Para la teoría de perturbaciones de primer orden, la expresión en Ecuación\ ref {2.123} es la solución a la ecuación diferencial que se obtiene para el acoplamiento directo entre\(| \ell \rangle\) y\(| k \rangle\):

\[\frac {\partial} {\partial t} b _ {k} = \frac {- i} {\hbar} e^{- i \omega _ {a x} t} V _ {k \ell} (t) b _ {\ell} ( 0 ) \label{2.125}\]

Esto indica que la solución no permite la retroalimentación entre\(| \ell \rangle\) y\(| k \rangle\) eso explica el cambio de poblaciones. Esta es la razón por la que decimos que la validez dicta

\[\left| b _ {k} (t) \right|^{2} - \left| b _ {k} ( 0 ) \right|^{2} \ll 1.\]

Si el estado inicial del sistema no\(\left|\psi_{0}\right\rangle\) es un estado propio de\(H_0\), podemos expresarlo como una superposición de autoestados,

\[b _ {k} (t) = \sum _ {n} b _ {n} ( 0 ) \left\langle k \left| U _ {I} \right| n \right\rangle \label{2.126}\]

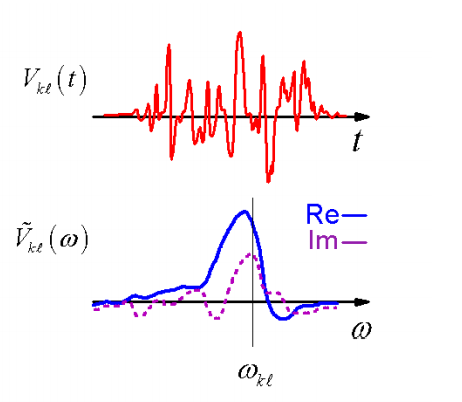
Otra observación se aplica a la teoría de perturbaciones de primer orden. Si el sistema se prepara inicialmente en un estado\(| \ell \rangle\), y una perturbación dependiente del tiempo se enciende y luego se apaga durante el intervalo de tiempo\(t=-\infty \text {to}+\infty\), entonces la amplitud compleja en el estado objetivo solo\(| k \rangle\) se relaciona con la transformada de Fourier de\(V_{\ell k}(t)\) evaluada en la brecha de energía \(\omega_{\ell k}\).

\[b _ {k} (t) = - \frac {i} {\hbar} \int _ {- \infty}^{+ \infty} d \tau \,e^{- i \omega _ {\ell k} \tau} V _ {k \ell} ( \tau ) \label{2.127}\]

Si el par de transformada de Fourier se define de la siguiente manera:

\[\tilde {V} ( \omega ) \equiv \tilde {\mathcal {F}} [ V (t) ] = \int _ {- \infty}^{+ \infty} d t \,V (t) \exp ( i \omega t ) \label{2.128}\]

\[V (t) \equiv \tilde {\mathcal {F}}^{- 1} [ \tilde {V} ( \omega ) ] = \frac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d \omega\, \tilde {V} ( \omega ) \exp ( - i \omega t ) \label{2.129}\]

Entonces podemos escribir la probabilidad de transferencia al estado\(k\) como

\[P _ {k \ell} = \frac {2 \pi \left| \tilde {V} _ {k \ell} \left( \omega _ {k \ell} \right) \right|^{2}} {\hbar^{2}} \label{2.130}\]

Ejemplo: Teoría de perturbaciones de primer orden

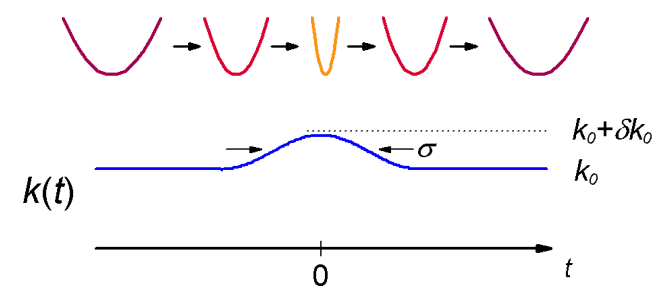
Consideremos un modelo simple para la excitación vibracional inducida por la compresión del oscilador armónico. Vamos a someter un oscilador armónico inicialmente en su estado fundamental a un pulso de compresión gaussiano, lo que aumenta su constante de fuerza.

Primero, escribe el hamiltoniano completo dependiente del tiempo:

\[H (t) = T + V (t) = \frac {p^{2}} {2 m} + \frac {1} {2} k (t) x^{2} \label{2.131}\]

Ahora, partirlo según de tal\(H=H_o + V(t) \) manera que podamos escribir\(H_o\) como un oscilador armónico hamiltoniano. Esto implica dividir la constante de fuerza dependiente del tiempo en dos partes:

\[k (t) = k _ {0} + \delta k (t)\]

\[k _ {0} = m \Omega^{2}\]

\[\delta k (t) = \delta k _ {0} \exp \left( - \frac {\left( t - t _ {0} \right)^{2}} {2 \sigma^{2}} \right) \label{2.133}\]

\[H=\underbrace{\frac{p^{2}}{2 m}+\frac{1}{2} k_{0} x^{2}}_{H_{0}}+\underbrace{\frac{1}{2} \delta k_{0} x^{2} \exp \left(-\frac{\left(t-t_{0}\right)^{2}}{2 \sigma^{2}}\right)}_{V(t)}\]

Aquí\(\delta k _ {0}\) está la magnitud del cambio inducido en la constante de fuerza, y\(\sigma\) es el ancho de tiempo de la perturbación gaussiana. Entonces, conocemos los estados propios de\(H_0\):\(H _ {0} | n \rangle = E _ {n} | n \rangle\)

\[H_{0}=\hbar \Omega\left(a^{\dagger} a+\frac{1}{2}\right)\]

y

\[E _ {n} = \hbar \Omega \left( n + \frac {1} {2} \right)\]

Ahora preguntamos, si el sistema está adentro\(|0\rangle\) antes de aplicar la perturbación, ¿cuál es la probabilidad de encontrarlo en el estado n después de la perturbación?

Para\(n \neq 0\)

\[b _ {n} (t) = \frac {- i} {\hbar} \int _ {t _ {0}}^{t} d \tau V _ {n 0} ( \tau ) e^{i \omega _ {n 0} \tau} \label{2.135}\]

Usando

\[\omega _ {n 0} = \left( E _ {n} - E _ {0} \right) / \hbar = n \Omega\]

y reconociendo que podemos establecer los límites para\(t_{0}=-\infty \text {and} \mathrm{t}=\infty\)

\[b _ {n} (t) = \frac {- i} {2 \hbar} \delta k _ {0} \left\langle n \left| x^{2} \right| 0 \right\rangle \int _ {- \infty}^{+ \infty} d \tau e^{i n \Omega \tau} e^{- \tau^{2} / 2 \sigma^{2}} \label{2.136}\]

Esto lleva a

\[b _ {n} (t) = \frac {- i} {2 \hbar} \delta k _ {0} \sqrt {2 \pi} \sigma \left\langle n \left| x^{2} \right| 0 \right\rangle e^{- n^{2} \sigma^{2} \Omega^{2} / 2} \label{2.137}\]

Aquí hicimos uso de una identidad importante para las integrales gaussianas:

\[\int _ {- \infty}^{+ \infty} \exp \left( a x^{2} + b x + c \right) d x = \sqrt {\frac {- \pi} {a}} \exp \left( c - \frac {1} {4} \frac {b^{2}} {a} \right) \label{2.138}\]

y

\[\int _ {- \infty}^{+ \infty} \exp \left( - a x^{2} + i b x \right) d x = \sqrt {\frac {\pi} {a}} \exp \left( - \frac {b^{2}} {4 a} \right) \label{2.139}\]

¿Qué pasa con el elemento matriz?

\[x^{2} = \frac {\hbar} {2 m \Omega} \left( a + a^{\dagger} \right)^{2} = \frac {\hbar} {2 m \Omega} \left( a a + a^{\dagger} a + a a^{\dagger} + a^{\dagger} a^{\dagger} \right)\label{2.140}\]

A partir de estos vemos que la teoría de perturbación de primer orden no permitirá transiciones a\(n =1\), solo\(n = 0\) y\(n = 2\). Generalmente esto no sería realista, porque ciertamente esperarías que la excitación\(n=1\) dominara sobre la excitación a\(n=2\). Un sistema real también sería anarmónico, en cuyo caso, el término principal en la expansión del potencial V (x), es decir lineal en x, no desaparecería como lo hace para un oscilador armónico, y esto conduciría a elementos matriciales que elevan y bajarían la excitación por un cuántico.

Sin embargo, para el presente caso,

\[\left\langle 2 \left| x^{2} \right| 0 \right\rangle = \sqrt {2} \frac {\hbar} {2 m \Omega} \label{2.141}\]

Entonces,

\[b _ {2} = \frac {- i \sqrt {\pi} \delta k _ {0} \sigma} {2 m \Omega} e^{- 2 \sigma^{2} \Omega^{2}} \label{2.142}\]

y podemos escribir la probabilidad de ocupar el\(n = 2\) estado como

\[P _ {2} = \left| b _ {2} \right|^{2} = \frac {\pi \delta k _ {0}^{2} \sigma^{2}} {2 m^{2} \Omega^{2}} e^{- 4 \sigma^{2} \Omega^{2}} \label{2.143}\]

A partir del argumento exponencial, se produce una transferencia significativa de amplitud cuando el ancho del pulso de compresión es pequeño en comparación con el período vibracional.

\[\sigma \ll \dfrac {1} {\Omega} \label{2.144}\]

En este régimen, el potencial está cambiando más rápido de lo que los átomos pueden responder a la perturbación. En la práctica, al considerar un problema de estado sólido, con frecuencias que coinciden con las de los fonones acústicos y las dimensiones de la celda unitaria, necesitamos perturbaciones que se muevan más rápido que la velocidad del sonido, es decir, una onda de choque. El límite opuesto,\(\sigma \Omega > > 1\), es el límite adiabático. En este caso, la perturbación es tan lenta que el sistema siempre permanece completamente en n=0, incluso mientras está comprimido.

Ahora, consideremos la validez de este tratamiento de primer orden. La teoría de la perturbación no\(b_n\) permite cambiar mucho de su valor inicial. Primero reescribimos la ecuación\ ref {2.143} como

\[P _ {2} = \sigma^{2} \Omega^{2} \frac {\pi} {2} \left( \frac {\delta k _ {0}^{2}} {k _ {0}^{2}} \right) e^{- 4 \sigma^{2} \Omega^{2}} \label{2.145}\]

Ahora para los cambios que no difieren mucho del valor inicial,\(P _ {2} \ll 1\)

\[\sigma^{2} \Omega^{2} \frac {\pi} {2} \left( \frac {\delta k _ {0}^{2}} {k _ {0}^{2}} \right) \ll 1 \label{2.146}\]

Generalmente, la magnitud de la perturbación\(\delta k _ {0}\) debe ser pequeña en comparación con\(k_0\).

Un paso más allá...

El ejemplo anterior fue simple, pero rastrea el enfoque general para configurar problemas que se tratan con la teoría de perturbación dependiente del tiempo. El enfoque se basa en escribir un hamiltoniano que se pueda convertir en un hamiltoniano que pueda tratar exactamente\(H_0\), y perturbaciones dependientes del tiempo que cambian las amplitudes entre sus propios estados. Para que este esquema funcione bien, necesitamos que la magnitud de la perturbación sea pequeña, lo que inmediatamente sugiere trabajar con una expansión del potencial de la serie Taylor. Por ejemplo, tomar un potencial unidimensional para una partícula unida\(V(x)\), que depende de la forma de una variable externa y. Podemos expandir el potencial en x alrededor de su mínimo\(x = 0\) como

\[\begin{align} V (x) &= \frac {1} {2 !} \left. \frac {\partial^{2} V} {\partial x^{2}} \right| _ {x = 0} x^{2} + \frac {1} {2 !} \left. \frac {\partial^{2} V} {\partial x \partial y} \right| _ {x = 0} x y + \frac {1} {3 !} \sum _ {y , z} \left. \frac {\partial^{3} V} {\partial x \partial y \partial z} \right| _ {x = 0} x y z + \cdots \label{2.147} \\ &= \frac {1} {2} k x^{2} + V^{( 2 )} x y + \left( V _ {3}^{( 3 )} x^{3} + V _ {2}^{( 3 )} x^{2} y + V _ {1}^{( 3 )} x y^{2} \right) + \cdots\end{align}\]

El primer término es la constante de fuerza armónica para\(x\), y el segundo término es un acoplamiento bi-lineal cuya magnitud\(V^{(2)}\) indica cuánto influye un cambio en la variable y en la variable\(x\). Los términos restantes son términos de expansión cúbica. \(V_3^{(3)}\)es la anarmonicidad cúbica de\(V(x)\), y los dos términos restantes son acoplamientos cúbicos que describen la dependencia de x e y. Introduciendo un potencial dependiente del tiempo equivale a introducir una dependencia del tiempo al operador y, donde la forma y la fuerza de la interacción se subsumen en la amplitud\(V\). En el caso del ejemplo anterior, nuestra formulación del problema fue equivalente a seleccionar sólo el\(V _ {2}^{( 3 )}\) término, de modo que\(\delta k _ {0} / 2 = V _ {2}^{( 3 )}\), y darle al valor de y una dependencia del tiempo descrita por la forma de onda gaussiana.

Lecturas

1. Cohen-Tannudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; p. 1285.
2. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Cap. 4.
3. Sakurai, J. J., Mecánica Cuántica Moderna, Edición Revisada. Addison-Wesley: Reading, MA, 1994; Ch. 2.