3.8: La regla de oro de Fermi

Una serie de relaciones importantes en la mecánica cuántica que describen los procesos de tasa provienen de la teoría de perturbaciones de primer orden. Estas expresiones comienzan con dos problemas de modelo que queremos resolver:

1. evolución del tiempo después de aplicar una perturbación escalonada, y
2. evolución del tiempo después de aplicar una perturbación armónica.

Como antes, preguntaremos: si preparamos el sistema en el estado\(| \ell \rangle\), ¿cuál es la probabilidad de observar el sistema en estado\(| k \rangle\) tras la perturbación?

Perturbación constante (o una perturbación escalonada)

El sistema se prepara de tal manera que\(| \psi ( - \infty ) \rangle = | \ell \rangle\). Se aplica una perturbación constante\(V\) de amplitud en\(t_o\):

\[V (t) = V \Theta \left( t - t _ {0} \right) = \left\{\begin{array} {l l} {0} & {t < t _ {0}} \\ {V} & {t \geq t _ {0}} \end{array} \right. \label{2.148}\]

Aquí\(\Theta \left( t - t _ {0} \right)\) está la función de respuesta de paso Heaviside, que es 0 para\(t < t_o\) y 1 para\(t ≥ t_0\). Ahora, volviendo a la teoría de perturbación de primer orden, la amplitud en\(k \neq \ell\), tenemos:

\[b _ {k} = - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau \,e^{i \omega _ {k l} \left( \tau - t _ {0} \right)} V _ {k \ell} ( \tau ) \label{2.149}\]

Aquí\(V_{k\ell}\) es independiente del tiempo.

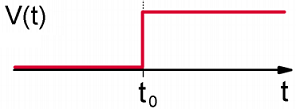
Ajuste\(t_o = 0\)

\[ \begin{align} b _ {k} &= - \frac {i} {\hbar} V _ {k \ell} \int _ {0}^{t} d \tau \,e^{i \omega _ {k \ell} \tau} \\[4pt] &= - \frac {V _ {k \ell}} {E _ {k} - E _ {\ell}} \left[ \exp \left( i \omega _ {k l} t \right) - 1 \right] \\[4pt] &= - \frac {2 i V _ {k \ell} e^{i \omega _ {k t} t / 2}} {E _ {k} - E _ {\ell}} \sin \left( \omega _ {k t} t / 2 \right) \label{2.150} \end{align}\]

Para la Ecuación\ ref {2.150}, se utilizó la siguiente identidad

\[e^{i \theta} - 1 = 2 i e^{i \theta / 2} \sin ( \theta / 2 ).\]

Ahora la probabilidad de estar en el\(k\) estado es

\[ \begin{align} P _ {k} &= \left| b _ {k} \right|^{2} \\[4pt] &= \frac {4 \left| V _ {k \ell} \right|^{2}} {\left| E _ {k} - E _ {\ell} \right|^{2}} \sin^{2} \left( \frac {\omega _ {k \ell} t} {2} \right) \label{2.151} \end{align}\]

Si escribimos esto usando la variable de división de energía que usamos anteriormente:

\[\Delta = \left( E _ {k} - E _ {t} \right) / 2\]

entonces

\[P _ {k} = \frac {V^{2}} {\Delta^{2}} \sin^{2} ( \Delta t / \hbar ) \label{2.152}\]

Afortunadamente, tenemos el resultado exacto para el problema de dos niveles para comparar esta aproximación con

\[P _ {k} = \frac {V^{2}} {V^{2} + \Delta^{2}} \sin^{2} \left( \sqrt {\Delta^{2} + V^{2}} t / \hbar \right) \label{2.153}\]

Al comparar la ecuación\ ref {2.152} y\ ref {2.153}, es claro que el resultado de la teoría de perturbación funciona bien para\(V \ll \Delta\), como se esperaba para este enfoque de aproximación.

Examinemos la dependencia del tiempo a\(P_k\), y comparemos la teoría de perturbación (líneas continuas) con el resultado exacto (líneas discontinuas) para diferentes valores de\(\Delta\).

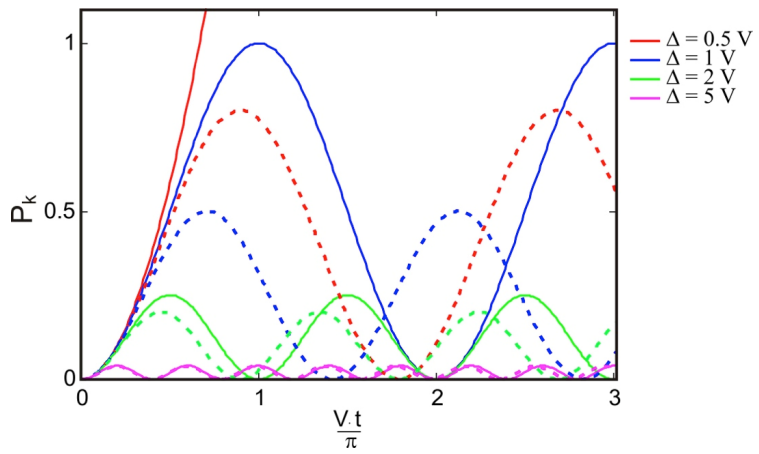
La peor correspondencia es para\(\Delta=0.5\) (curvas rojas) para las cuales el comportamiento aparece cuadrático y la probabilidad supera rápidamente la unidad. Ciertamente es poco realista, pero no esperamos que la expresión se mantenga para el caso del “acoplamiento fuerte”:\(\Delta \ll V\). Uno comienza a tener precisión cuantitativa en para el régimen\(P _ {k} (t) - P _ {k} ( 0 ) < 0.1\) o\(\Delta < 4V\).

Ahora veamos la dependencia de\(\Delta\). Podemos escribir el resultado de primer orden Ecuación\ ref {2.152} como

\[P _ {k} = \frac {V^{2} t^{2}} {\hbar^{2}} \text{sinc}^{2} ( \Delta t / 2 \hbar ) \label{2.154}\]

donde

\[\text{sinc} (x) = \dfrac{\sin (x)}{x}.\]

Si trazamos la probabilidad de transferencia de\(| \ell \rangle\) a\(| k \rangle\) como una función del nivel de energía splitting (\(E_k-K_{\ell}\)), tenemos:

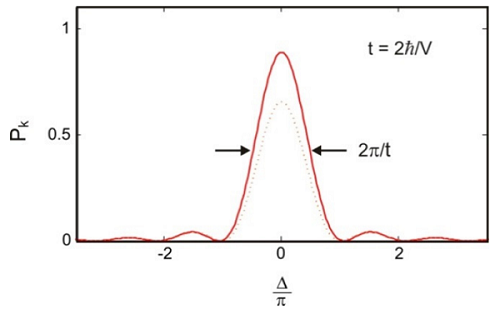
La probabilidad de transferencia alcanza un pico brusco donde la energía del estado inicial coincide con la del estado final, y el ancho de la falta de coincidencia de energía se estrecha con el tiempo. Desde

\[\lim _ {x \rightarrow 0} \operatorname {sinc} (x) = 1,\]

vemos que el comportamiento a corto plazo es un crecimiento cuadrático en\(P_k\)

\[\lim _ {\Delta \rightarrow 0} P _ {k} = \dfrac{V^{2} t^{2}}{\hbar^{2}} \label{2.155}\]

El área integrada crece linealmente con el tiempo.

Incertidumbre

Dado que la dispersión energética de los estados a los que la transferencia es eficiente escala aproximadamente como\(E _ {k} - E _ {\ell} < 2 \pi \hbar / t\), a esta observación se le denomina a veces una relación de incertidumbre con

\[\Delta E \cdot \Delta t \geq 2 \pi \hbar\]

Sin embargo, recuerde que esto es realmente solo una observación de los principios de las transformadas de Fourier. Una frecuencia solo se puede determinar con la misma precisión que la duración del tiempo durante el cual se observan oscilaciones. Como el tiempo no es un operador, no es una verdadera relación insegura como

\[\Delta p \cdot \Delta x \geq 2 \pi \hbar.\]

En el límite de tiempo largo, la\(\text{sinc}^2 (x)\) función se reduce a una función delta:

\[\lim _ {t \rightarrow \infty} \frac {\sin^{2} ( a x / 2 )} {a x^{2}} = \frac {\pi} {2} \delta (x) \label{2.156}\]

Entonces la probabilidad de mucho tiempo de estar en el\(k\) estado es

\[\lim _ {t \rightarrow \infty} P _ {k} (t) = \frac {2 \pi} {\hbar} \left| V _ {k \ell} \right|^{2} \delta \left( E _ {k} - E _ {\ell} \right) t \label{2.157}\]

La función delta hace cumplir la conservación de energía, diciendo que las energías del estado inicial y objetivo deben ser las mismas en el límite de tiempo largo. Lo interesante en la Ecuación\ ref {2.157} es que vemos una probabilidad creciendo linealmente en el tiempo. Esto sugiere una tasa de transferencia que es independiente del tiempo, como se esperaba para la cinética simple de primer orden:

\[w _ {k} (t) = \frac {\partial P _ {k} (t)} {\partial t} = \frac {2 \pi \left| V _ {k \ell} \right|^{2}} {\hbar} \delta \left( E _ {k} - E _ {\ell} \right) \label{2.158}\]

Esta es una declaración de la regla de oro de Fermi, la forma de estado a estado, que describe las tasas de relajación de la teoría de perturbación de primer orden. Mostraremos que esta tasa describe adecuadamente las tasas de relajación exponencial de largo tiempo que esperaría de la solución a

\[\dfrac{d P}{d t} = - w P.\]

Perturbación armónica

El segundo cálculo del modelo es la interacción de un sistema con una perturbación oscilante encendida en el momento\(t_0 = 0\). Los resultados se utilizarán para describir cómo un campo de luz induce transiciones en un sistema a través de interacciones dipolares.

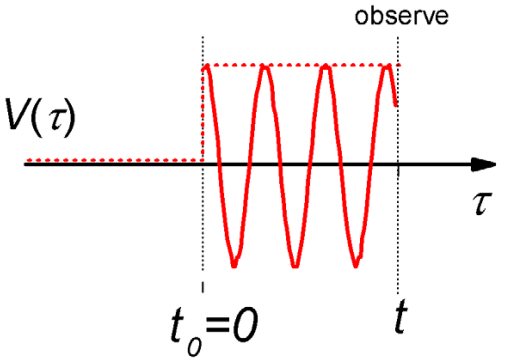
Nuevamente, estamos buscando calcular la probabilidad de transición entre estados\(\ell\) y\(k\):

\[V (t) = V \cos \omega t \Theta (t) \label{2.159}\]

\[ \begin{align} V _ {k \ell} (t) &= V _ {k \ell} \cos \omega t \label{2.160} \\[4pt] &= \frac {V _ {k \ell}} {2} \left[ e^{- i \omega t} + e^{i \omega t} \right] \end{align}\]

Configuración\(t _ {0} \rightarrow 0\), teoría de perturbación de primer orden conduce a

\[ \begin{align} b _ {k} &= \frac {- i} {\hbar} \int _ {t _ {0}}^{t} d \tau\, V _ {k \ell} ( \tau ) e^{i \omega _ {k l} \tau} \\[4pt] &= \frac {- i V _ {k \ell}} {2 \hbar} \int _ {0}^{t} d \tau \left[ e^{i \left( \omega _ {k l} - \omega \right) \tau} + e^{i \left( \omega _ {k l} + \omega \right) \tau} \right] \\[4pt] &= \frac {- i V _ {k \ell}} {2 \hbar} \left[ \frac {e^{i \left( \omega _ {k l} - \omega \right) t} - 1} {\omega _ {k \ell} - \omega} + \frac {e^{i \left( \omega _ {k t} + \omega \right) t} - 1} {\omega _ {k \ell} + \omega} \right] \end{align} \]

Usando

\[e^{\theta} - 1 = 2 i e^{i \theta / 2} \sin ( \theta / 2 )\]

como antes:

\[b _ {k} = \frac {V _ {k \ell}} {\hbar} \left[ \underbrace{\frac {e^{i \left( \omega _ {k \ell} - \omega \right) t / 2} \sin \left[ \left( \omega _ {k \ell} - \omega \right) t / 2 \right]} {\omega _ {k \ell} - \omega}}_{\text{absorption}} + \underbrace{\frac {e^{i \left( \omega _ {k \ell} + \omega \right) t / 2} \sin \left[ \left( \omega _ {k \ell} + \omega \right) t / 2 \right]} {\omega _ {k \ell} + \omega}}_{\text{stimulated emission}} \right] \label{2.162}\]

Observe que estos términos sólo son significativos cuando\(\omega \approx \pm \omega _ {k \ell}\). La condición para una transferencia eficiente es la resonancia, una coincidencia de la frecuencia de la interacción armónica con la división de energía entre estados cuánticos. Considere las condiciones de resonancia que maximizarán cada una de estas:

Si consideramos únicamente la absorción,

\[P _ {k \ell} = \left| b _ {k} \right|^{2} = \frac {\left| V _ {k l} \right|^{2}} {\hbar^{2} \left( \omega _ {k t} - \omega \right)^{2}} \quad \sin^{2} \left[ \frac {1} {2} \left( \omega _ {k \ell} - \omega \right) t \right] \label{2.163}\]

Podemos comparar esto con la expresión exacta:

\[P _ {k \ell} = \left| b _ {k} \right|^{2} = \frac {\left| V _ {k l} \right|^{2}} {\hbar^{2} \left( \omega _ {k t} - \omega \right)^{2} + \left| V _ {k l} \right|^{2}} \sin^{2} \left[ \frac {1} {2 \hbar} \sqrt {\left| V _ {k l} \right|^{2} + \left( \omega _ {k \ell} - \omega \right)^{2}} t \right] \label{2.164}\]

Nuevamente, vemos que la expresión de primer orden es válida para acoplamientos\(\left| V _ {k \ell} \right|\) que son pequeños en relación con el desintonizado\(\Delta \omega = \left( \omega _ {k \ell} - \omega \right)\). La probabilidad máxima de transferencia está en resonancia\(\omega _ {k \ell} = \omega\)

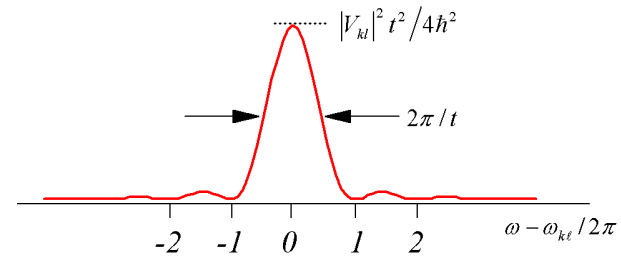
Similar a nuestra descripción de la perturbación constante, el límite de tiempo largo para esta expresión conduce a una función delta\(\delta \left( \omega _ {k \ell} - \omega \right)\). En este largo límite de tiempo, podemos descuidar las interferencias entre los términos resonante y antirresonante. Las tasas de transiciones entre\(k\) y\(\ell\) estados determinados a partir de\(w _ {k \ell} = \partial P _ {k} / \partial t\) se convierte

\[w _ {k \ell} = \frac {\pi} {2 \hbar^{2}} \left| V _ {k \ell} \right|^{2} \left[ \delta \left( \omega _ {k \ell} - \omega \right) + \delta \left( \omega _ {k \ell} + \omega \right) \right] \label{2.165}\]

Podemos examinar las limitaciones de esta fórmula. Cuando buscamos el comportamiento en resonancia, expandir el pecado (x) nos muestra que Pk se eleva cuadráticamente por tiempos cortos:

\[\lim _ {\Delta \omega \rightarrow 0} P _ {k} (t) = \frac {\left| V _ {k \ell} \right|^{2}} {4 \hbar^{2}} t^{2} \label{2.166}\]

Esto claramente no describirá el comportamiento a largo plazo, pero se mantendrá para pequeños\(P_k\), por lo que requerimos

\[t \ll \frac {2 \hbar} {V _ {k \ell}} \label{2.167}\]

Al mismo tiempo, no podemos observar el sistema en una escala de tiempo demasiado corta. Necesitamos que el campo haga varias oscilaciones para que esto se considere una perturbación armónica.

\[t > \frac {1} {\omega} \approx \frac {1} {\omega _ {k \ell}} \label{2.168}\]

Estas relaciones implican que requerimos

\[V _ {k \ell} \ll \hbar \omega _ {k \ell} \label{2.169}\]

Lecturas

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; p. 1299.
2. McHale, J. L., Espectroscopia Molecular. 1a ed.; Prentice Hall: Upper Saddle River, NJ, 1999; Ch. 4.
3. Sakurai, J. J., Mecánica Cuántica Moderna, Edición Revisada. Addison-Wesley: Reading, MA, 1994.