10.3: Funciones cuánticas de correlación temporal

Las funciones de correlación cuántica implican el promedio de equilibrio (térmico) sobre un producto de operadores hermitianos evaluados dos veces. El promedio térmico está implícito en la escritura

\[C _ {A A} ( \tau ) = \langle A ( \tau ) A ( 0 ) \rangle.\]

Naturalmente, esto también invoca una representación de Heisenberg de los operadores, aunque en casi todos los casos, estaremos escribiendo funciones de correlación como operadores de imagen de interacción

\[A _ {I} (t) = e^{i H _ {0} t} A e^{- i H _ {0} t}.\]

Para enfatizar el promedio térmico, la función de correlación cuántica también se puede escribir como

\[C _ {A A} ( \tau ) = \left\langle \frac {e^{- \beta H}} {Z} A ( \tau ) A ( 0 ) \right\rangle \label{9.18}\]

con\(\beta = \left( k _ {\mathrm {B}} T \right)^{- 1}\). Si evaluamos esto para un hamiltoniano independiente del tiempo en una base de estados n, insertar un operador de proyección conduce a nuestra expresión anterior

\[C _ {A A} ( \tau ) = \sum _ {n} p _ {n} \langle n | A ( \tau ) A ( 0 ) | n \rangle \label{9.19}\]

con\(p _ {n} = e^{- \beta E _ {n}} / Z\). Dado el caso de un hamiltoniano independiente del tiempo para el que tenemos conocimiento de los autoestados, también podemos expresar la función de correlación en la imagen de Schrödinger como

\[\begin{align} C _ {A A} ( \tau ) &= \sum _ {n} p _ {n} \left\langle n \left| U^{\dagger} ( \tau ) A U ( \tau ) A \right| n \right\rangle \\[4pt] &= \sum _ {n , m} p _ {n} \langle n | A | m \rangle \langle m | A | n \rangle e^{- i \omega _ {m n} \tau} \\[4pt] &= \sum _ {n , m} p _ {n} \left| A _ {m n} \right|^{2} e^{- i \omega _ {m n} \tau} \label{9.20} \end{align}\]

Propiedades de las funciones de correlación cuántica

Existen algunas propiedades de las funciones de correlación cuántica para los operadores hermitianos que se pueden obtener usando las propiedades del operador de evolución temporal. Primero, podemos mostrar que las funciones de correlación son estacionarias:

\[\left.\begin{aligned} \left\langle A (t) A \left( t^{\prime} \right) \right\rangle & = \left\langle U^{\dagger} (t) A ( 0 ) U (t) U^{\dagger} \left( t^{\prime} \right) A ( 0 ) U \left( t^{\prime} \right) \right\rangle \\[4pt] & = \left\langle U \left( t^{\prime} \right) U^{\dagger} (t) A U (t) U^{\dagger} \left( t^{\prime} \right) A \right\rangle \\[4pt] & = \left\langle U^{\dagger} \left( t - t^{\prime} \right) A U \left( t - t^{\prime} \right) A \right\rangle \\[4pt] & = \left\langle A \left( t - t^{\prime} \right) A ( 0 ) \right\rangle \end{aligned} \right. \label{9.21}\]

Del mismo modo, podemos mostrar

\[\langle A ( - t ) A ( 0 ) \rangle = \langle A (t) A ( 0 ) \rangle^{*} = \langle A ( 0 ) A (t) \rangle \label{9.22}\]

o en resumen

\[C _ {A A}^{*} (t) = C _ {A A} ( - t ) \label{9.23}\]

Tenga en cuenta que el cuántico\(C_{AA}(t)\) es complejo. No se puede medir directamente una función de correlación cuántica, pero los observables suelen estar relacionados con la parte real o imaginaria de las funciones de correlación.

\[C _ {A A} (t) = C _ {A A}^{\prime} (t) + i C _ {A A}^{\prime \prime} (t) \label{9.24}\]

Las partes reales e imaginarias de se\(C_{AA}(t)\) pueden separar como

\[\left.\begin{aligned} C _ {A A}^{\prime} (t) & = \frac {1} {2} \left[ C _ {A A} (t) + C _ {A A}^{*} (t) \right] = \frac {1} {2} [ \langle A (t) A ( 0 ) \rangle + \langle A ( 0 ) A (t) \rangle ] \\[4pt] & = \frac {1} {2} \left\langle [ A (t) , A ( 0 ) ] _ {+} \right\rangle \end{aligned} \right. \label{9.25}\]

\[\left.\begin{aligned} C _ {A A}^{\prime \prime} (t) & = \frac {1} {2} \left[ C _ {A A} (t) - C _ {A A}^{*} (t) \right] = \frac {1} {2} [ \langle A (t) A ( 0 ) \rangle - \langle A ( 0 ) A (t) \rangle ] \\[4pt] & = \frac {1} {2} \langle [ A (t) , A ( 0 ) ] \rangle \end{aligned} \right. \label{9.26}\]

Arriba\([ A , B ] _ {+} \equiv A B + B A\) está el anticonmutador. Como se ilustra a continuación, la parte real es par en el tiempo, y se puede expandir como series de Fourier en cosenos, mientras que la parte imaginaria es impar, y puede expandirse en senos. Veremos más adelante que la magnitud de la parte real crece con la temperatura, pero lo imaginario no. A 0 K, los componentes real e imaginario tienen amplitudes iguales, pero a medida que uno se acerca al límite de temperatura alta o clásico, la parte real domina lo imaginario.

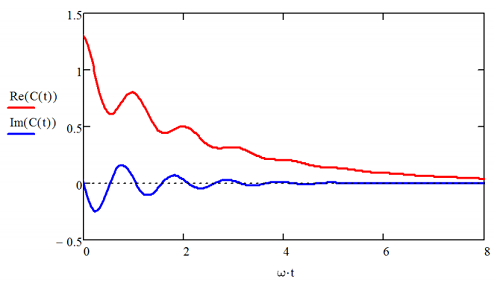
También veremos en nuestra discusión de respuesta lineal que\(C'_{AA}\) y\(C''_{AA}\) son directamente proporcionales a la función de respuesta escalonada\(S\) y a la función de respuesta de impulso\(R\), respectivamente. \(R\)describe cómo un sistema es alejado del equilibrio por un potencial externo, mientras que\(S\) describe la relajación del sistema al equilibrio cuando se libera una fuerza que lo mantiene alejado del equilibrio. Clásicamente, los dos están relacionados por\(R \propto \partial S / \partial t\).

Dado que el tiempo y la frecuencia son variables conjugadas, también podemos definir una función de correlación espectral o de dominio de frecuencia mediante la transformación de Fourier del TCF. La transformada de Fourier y su inversa se definen como

\[ \begin{align} \tilde {C} _ {A A} ( \omega ) &= \tilde {\mathcal {F}} \left[ C _ {A A} (t) \right] \\[4pt] &= \int _ {- \infty}^{+ \infty} \mathrm {e}^{i \omega t} C _ {A A} (t) \,d t \label{9.27} \end{align}\]

\[\begin{align} C _ {A A} (t) &= \tilde {\mathcal {F}}^{- 1} \left[ \tilde {C} _ {A A} ( \omega ) \right] \\[4pt] &= \frac {1} {2 \pi} \int _ {- \infty}^{+ \infty} \mathrm {e}^{- i \omega t} \tilde {C} _ {A A} ( \omega ) \,d \omega \label{9.28} \end{align}\]

A continuación se muestran ejemplos de las funciones de correlación en el dominio de la frecuencia.

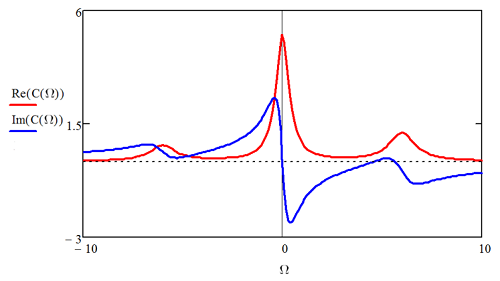
Para un hamiltoniano independiente del tiempo, como podríamos tener en un problema de imagen de interacción, la transformada de Fourier del TCF en la Ecuación\ ref {9.20} da

\[\tilde {C} _ {A A} ( \omega ) = \sum _ {n , m} p _ {n} \left| A _ {m n} \right|^{2} \delta \left( \omega - \omega _ {m n} \right) \label{9.29}\]

Esta expresión se parece mucho a la tasa de transición de la Regla de Oro de la teoría de perturbaciones de primer orden. De hecho, la transformada de Fourier de funciones de correlación temporal evaluadas en la brecha de energía da la tasa de transición entre estados que obtenemos de la teoría de perturbación de primer orden. Tenga en cuenta que esta expresión es válida tanto si los estados iniciales\(n\) son más altos o menores en energía que los estados finales\(m\), y da cuenta de las transiciones ascendentes y descendentes. Si comparamos la relación de las tasas de transición ascendente y descendente entre dos estados\(i\) y\(j\), tenemos

\[\frac {\tilde {C} _ {A A} \left( \omega _ {i j} \right)} {\tilde {C} _ {A A} \left( \omega _ {j i} \right)} = \frac {p _ {j}} {p _ {i}} = e^{\beta E _ {j}} \label{9.30}\]

Esta es una forma de mostrar el principio de equilibrio detallado, que relaciona las tasas de transición ascendente y descendente en equilibrio con la diferencia en la ocupación térmica entre estados:

\[\tilde {C} _ {A A} ( \omega ) = e^{\beta \hbar \omega} \tilde {C} _ {A A} ( - \omega ) \label{9.31}\]

Esta relación junto con una transformada de Fourier de la Ecuación\ ref {9.23} nos permite obtener los componentes reales e imaginarios usando

\[\tilde {C} _ {A A} ( \omega ) \pm \tilde {C} _ {A A} ( - \omega ) = \left( 1 \pm e^{- \beta \hbar \omega} \right) \tilde {C} _ {A A} ( \omega ) \label{9.32}\]

\[\tilde {C} _ {A A}^{\prime} ( \omega ) = \tilde {C} _ {A A} ( \omega ) \left( 1 + e^{- \beta \hbar \omega} \right) \label{9.33}\]

\[\tilde {C} _ {A A}^{\prime \prime} ( \omega ) = \tilde {C} _ {A A} ( \omega ) \left( 1 - e^{- \beta \hbar \omega} \right) \label{9.34}\]