11.4: Relajación de un Estado Preparado
- Page ID
- 74145
La función de respuesta al impulso\(R(t)\) describe el comportamiento de un sistema inicialmente en equilibrio que es impulsado por un campo externo. Alternativamente, es posible que necesitemos describir la relajación de un estado preparado, en el que seguimos el retorno al equilibrio de un sistema inicialmente mantenido en un estado de no equilibrio. Este comportamiento se describe mediante la función de respuesta paso a paso\(S(t)\). La respuesta de paso viene de mantener el sistema con un campo constante\(H = H _ {0} - f A\) hasta un\(t_0\) momento en que se libera el sistema, y se relaja al estado de equilibrio gobernado por\(H=H_o\).
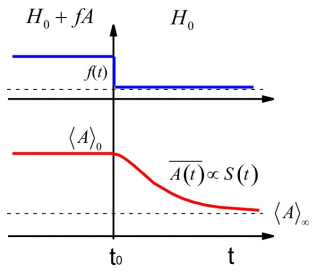
Podemos anticipar que las formas de estas dos funciones están relacionadas. Así como esperamos que la respuesta de impulso suba de cero y se exprese como una función impar en el tiempo, la respuesta de paso debería decairse desde un valor fijo y verse pareja en el tiempo. De hecho, podríamos esperar describir la respuesta al impulso diferenciando la respuesta escalonada, como se ve en el caso clásico.
\[R (t) = \frac {1} {k T} \frac {d} {d t} S (t) \label{10.72}\]
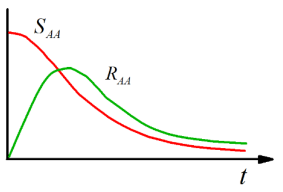
Una derivación empírica de la respuesta escalonada comienza con algunas observaciones. Primero, las funciones de respuesta deben ser reales ya que son proporcionales a los observables, sin embargo, las funciones de correlación cuántica son complejas y siguen
\[C ( - t ) = C^{*} (t).\]
Las funciones clásicas de correlación son reales e incluso,
\[C (t) = C ( - t )\]
y tienen las propiedades de una respuesta escalonada. Para obtener la relajación de un observable real que es incluso en el tiempo, podemos construir una función simétrica, que es solo la parte real de la función de correlación:
\[\begin{align} S _ {A A} (t) & = \frac {1} {2} \left\{\left\langle A _ {I} (t) A _ {I} ( 0 ) \right\rangle + \left\langle A _ {I} ( 0 ) A _ {I} (t) \right\rangle \right\} \\ & = \frac {1} {2} \left\{C _ {A A} (t) + C _ {A A} ( - t ) \right\} \\ & = C _ {A A}^{\prime} (t) \end{align} \label{10.74}\]
La función de respuesta de paso\(S\) se define de la siguiente manera para\(t \ge 0\).
\[S ( \tau ) \equiv \frac {1} {\hbar} \Theta ( \tau ) \left\langle \left[ A _ {I} ( \tau ) , A _ {I} ( 0 ) \right] \right\rangle _ {+}\]
A partir de la representación autoestatal de la función de correlación,
\[C (t) = \sum _ {n , m} p _ {n} \left| A _ {m n} \right|^{2} e^{- i \omega _ {m n} t} \label{10.75}\]
vemos que la función de respuesta escalonada se puede expresar como una expansión en cosenos
\[S (t) = \frac {2} {\hbar} \Theta (t) \sum _ {n , m} p _ {n} \left| A _ {m n} \right|^{2} \cos \omega _ {m n} t \label{10.76}\]
Además, se puede demostrar fácilmente que las partes reales e imaginarias están relacionadas por
\[ \begin{align} \omega \dfrac {d C^{\prime}} {d t} &= C^{\prime \prime} \\[4pt] \omega \dfrac {d C^{\prime \prime}} {d t} &= C^{\prime} \end{align} \label{10.77}\]
Lo que muestra cómo se relaciona la respuesta de impulso con la derivada de tiempo de la respuesta escalonada.
En el dominio de frecuencia, la representación espectral de la respuesta escalonada se obtiene de la transformada de Fourier—Laplace
\[S _ {A A} ( \omega ) = \int _ {0}^{\infty} d t S _ {A A} (t) e^{i \omega t} \label{10.78}\]
\[\begin{align} S _ {A A} ( \omega ) & = \frac {1} {2} \left[ C _ {A A} ( \omega ) + C _ {A A} ( - \omega ) \right] \\ & = \frac {1} {2} \left( 1 + e^{- \beta \hbar \omega} \right) C _ {A A} ( \omega ) \label{10.79} \end{align}\]
Ahora, con la expresión para la parte imaginaria de la susceptibilidad,
\[\chi^{\prime \prime} ( \omega ) = \frac {1} {2 \hbar} \left( 1 - e^{- \beta \hbar \omega} \right) C _ {AA} ( \omega ) \label{10.80} \]
obtenemos la relación
\[\chi^{\prime \prime} ( \omega ) = \frac {1} {\hbar} \tanh \left( \frac {\beta \hbar \omega} {2} \right) S _ {A A} ( \omega ) \label{10.81}\]
La ecuación\ ref {10.81} es la expresión formal para el teorema de fluctuación-disipación, probado en 1951 por Callen y Welton. Siguió una observación hecha muchos años antes (1930) por Lars Onsager por la que fue galardonado con el Premio Nobel de Química de 1968: “La relajación de la perturbación macroscópica del desequilibrio se rige por las mismas leyes que la regresión de las fluctuaciones microscópicas espontáneas en un estado de equilibrio”.
Señalando que
\[\tanh (x) = \dfrac{e^{x} - e^{- x}}{e^{x} + e^{- x}}\]
y
\[\tanh (x) \rightarrow x\]
para\(x \gg 1\), vemos que en el límite de alta temperatura (clásico)
\[\chi^{\prime \prime} ( \omega ) \Rightarrow \frac {1} {2 k T} \omega S _ {A A} ( \omega ) \label{10.82}\]
Apéndice: Derivación de la función de respuesta escalonada
Podemos mostrar de manera más directa cómo se relacionan el impulso y la respuesta escalonada. Para comenzar, consideremos el experimento de respuesta escalonada,
\[H = \left\{\begin{array} {l l} {H _ {0} - f A} & {t < 0} \\ {H _ {0}} & {t \geq 0} \end{array} \right. \label{10.83}\]
y escribir los valores de expectativa de la variable interna A para el sistema equilibrada bajo\(H\) en tiempo\(t = 0\) y\(t = ∞\).
\[\langle A \rangle _ {0} = \left\langle \frac {e^{- \beta \left( H _ {0} - f A \right)}} {Z _ {0}} A \right\rangle \label{10.84A}\]
con
\[Z _ {0} = \left\langle e^{- \beta \left( H _ {0} - f A \right)} \right\rangle \label{10.84B}\]
y
\[\langle A \rangle _ {\infty} = \left\langle \frac {e^{- \beta H _ {0}}} {Z _ {\infty}} A \right\rangle \label{10.85A}\]
con
\[Z _ {\infty} = \left\langle e^{- \beta H _ {0}} \right\rangle \label{10.85B}\]
Si hacemos la aproximación de respuesta lineal clásica, que establece que cuando el potencial aplicado\(fA\) es muy pequeño en relación con\(0_o\), entonces
\[e^{- \beta \left( H _ {0} - f A \right)} \approx e^{- \beta H _ {0}} ( 1 + \beta f A ) \label{10.86}\]
y\(Z _ {0} \approx Z _ {\infty}\), que
\[\delta A = \langle A \rangle _ {0} - \langle A \rangle _ {\infty} \approx \beta f \left\langle A^{2} \right\rangle \label{10.87}\]
y la relajación dependiente del tiempo viene dada por la función de correlación clásica
\[\delta A (t) = \beta f \langle A ( 0 ) A (t) \rangle \label{10.88}\]
Para una descripción que funcione para el caso cuántico, comencemos con el sistema debajo de\(H_o\) at\(t=-∞\), aumentemos el potencial externo a una velocidad lenta\(\eta\) hasta\(t=0\), y luego apagemos abruptamente el potencial externo y veamos el sistema. Describiremos el comportamiento en el límite\(\eta → 0\).
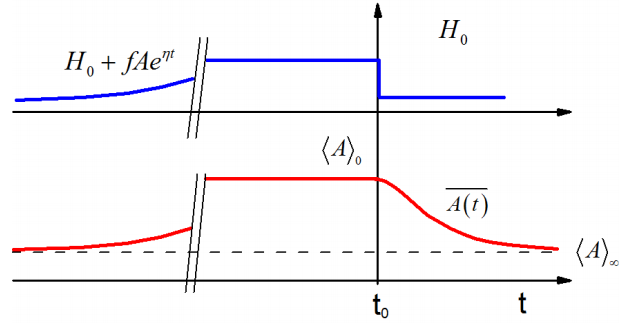
\[H = \left\{\begin{array} {l l} {H _ {0} + f A e^{\eta t}} & {t < 0} \\ {H _ {0}} & {t \geq 0} \end{array} \right. \label{10.89}\]
Escribiendo la dependencia del tiempo en términos de una convolución sobre la función de respuesta al impulso\(R\), tenemos
\[\overline {\delta A (t)} = \lim _ {\eta \rightarrow 0} \int _ {- \infty}^{0} d t^{\prime} \Theta \left( t - t^{\prime} \right) R \left( t - t^{\prime} \right) e^{\eta t^{\prime}} f \label{10.90}\]
Aunque la integral sobre la fuerza aplicada (t') es a lo largo de los tiempos t<0, el factor de respuesta escalonada asegura que t≥0. Ahora, expresando R como una transformada de Fourier sobre la parte imaginaria de la susceptibilidad, obtenemos
\[\left.\begin{aligned} \overline {\delta A (t)} & = \lim _ {\eta \rightarrow 0} \frac {f} {2 \pi} \int _ {- \infty}^{0} d t^{\prime} \int _ {- \infty}^{\infty} d \omega e^{( \eta - i \omega ) t^{\prime}} e^{i \omega t} \chi^{\prime \prime} ( \omega ) \\ & = \frac {f} {2 \pi} \int _ {- \infty}^{\infty} d \omega P P \left( \frac {1} {- i \omega} \right) \chi^{\prime \prime} ( \omega ) e^{i \omega t} \\ & = \frac {f} {2 \pi i} \int _ {- \infty}^{\infty} d \omega \chi^{\prime} ( \omega ) e^{i \omega t} \\ & = f C^{\prime} (t) \end{aligned} \right. \label{10.91}\]
Una derivación más cuidadosa de este resultado que trata adecuadamente a los operadores mecánicos cuánticos se encuentra en las referencias.
Lecturas
- Mazenko, G., Mecánica Estadística de No Equilibrio. Wiley-VCH: Weinheim, 2006.
- Zwanzig, R., Mecánica Estadística de No Equilibrio. Oxford University Press: Nueva York, 2001.

