14.3: Modelo Gaussiano-Estocástico para Difusión Espectral

Comenzaremos con una descripción clásica de cómo las fluctuaciones aleatorias en la frecuencia influyen en la forma de línea de absorción, calculando la función de correlación dipolo para la transición resonante. Este es un modelo estocástico gaussiano para fluctuaciones, lo que significa que describiremos la dependencia del tiempo de la energía de transición como fluctuaciones aleatorias alrededor de un valor promedio a través de una distribución gaussiana.

\[ \begin{align} \omega (t) &= \langle \omega \rangle + \delta \omega (t) \label{13.9} \\[4pt] \langle \delta \omega (t) \rangle &= 0 \label{13.10} \end{align}\]

Las fluctuaciones en\(\omega\) permiten al sistema explorar una distribución gaussiana de frecuencias de transición caracterizada por una varianza:

\[\Delta = \sqrt {\left\langle \omega^{2} \right\rangle - \langle \omega \rangle^{2}} = \sqrt {\left\langle \delta \omega^{2} \right\rangle} \label{13.11}\]

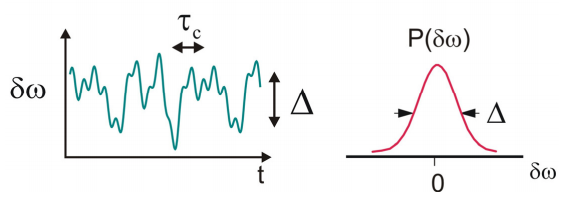
En muchas figuras el ancho de la distribución gaussiana se etiqueta con la desviación estándar (aquí\(\Delta\)). Esto pretende simbolizar ese\(\Delta\) es el parámetro que determina el ancho, y no que sea el ancho de línea. Para las distribuciones gaussianas, el ancho de línea completo a la mitad de la amplitud máxima (FWHM) es\(2.35 \Delta\).

Las escalas de tiempo para los desplazamientos de frecuencia se describirán en términos de una función de correlación de frecuencia.

\[C _ {\delta \omega s \omega} (t) = \langle \delta \omega (t) \delta \omega ( 0 ) \rangle \label{13.12}\]

Además, describiremos la escala de tiempo de las fluctuaciones aleatorias a través de un tiempo de correlación\(\tau_c\).

La forma de línea de absorción se describe con una función de correlación de tiempo dipolo. Tratemos el momento dipolar como una variable interna al sistema, cuyo valor depende del de\(\omega\). Cualitativamente, es posible escribir una ecuación de movimiento para\(\mu\) asociando el momento dipolar con el desplazamiento de una partícula ligada (\(x\)) veces su carga, y utilizando nuestra intuición sobre cómo se comporta el sistema. Para un estado imperturbable, esperamos que\(x\) oscile a una frecuencia\(\omega\), pero con perturbaciones, variará a través de la distribución de frecuencias disponibles. Una función que tiene este comportamiento es

\[x (t) = x _ {0} e^{- i \omega (t) t} \label{13.13}\]

Si diferenciamos esta ecuación con respecto al tiempo y multiplicamos por carga tenemos

\[\frac {\partial \mu} {\partial t} = - i \omega (t) \mu (t) \label{13.14}\]

Aunque es una ecuación clásica, observe la similitud con la ecuación cuántica de Heisenberg para el operador dipolo:

\[\partial \mu / \partial t = i H (t) \mu / \hbar + h . c .\]

La correspondencia de\(\omega (t)\) con\(H (t) / \hbar\) ofrece una idea de cómo se verá la versión cuántica de este problema.

La solución a la Ecuación\ ref {13.14} es

\[\mu (t) = \mu ( 0 ) \exp \left[ - i \int _ {0}^{t} d \tau \, \omega ( \tau ) \right] \label{13.15}\]

Sustituyendo esta expresión y la Ecuación\ ref {13.9} en la función de correlación dipolo da o

\[C _ {\mu \mu} (t) = | \mu |^{2} e^{- i \langle \omega \rangle t} F (t) \label{13.16}\]

donde

\[F (t) = \left\langle \exp \left[ - i \int _ {0}^{t} d \tau \, \delta \omega ( \tau ) \right] \right\rangle \label{13.17}\]

La función de desfase (\(F(t)\)) se obtiene realizando un promedio de equilibrio del argumento exponencial sobre trayectorias fluctuantes. Para los sistemas ergódicos, esto equivale a promediar el tiempo suficiente en una sola trayectoria.

La función de desfase es un poco complicada de trabajar como está escrita. Sin embargo, para el caso de la estadística gaussiana para las fluctuaciones, es posible simplificarla\(F(t)\) expandiéndola como una expansión acumulante de promedios (ver apéndice a continuación para más detalles).

\[F (t) = \exp \left[ - i \int _ {0}^{t} d \tau^{\prime} \, \left\langle \delta \omega \left( \tau^{\prime} \right) \right\rangle + \frac {i^{2}} {2 !} \int _ {0}^{t} d \tau^{\prime} \, \int _ {0}^{t} d \tau^{\prime \prime} \, \left\{\left\langle \delta \omega \left( \tau^{\prime} \right) \delta \omega \left( \tau^{\prime \prime} \right) \right\rangle - \left\langle \delta \omega \left( \tau^{\prime} \right) \right\rangle \left\langle \delta \omega \left( \tau^{\prime \prime} \right) \right\rangle \right\} \right] \label{13.18}\]

En esta expresión, el primer término es cero, ya que\(\langle \delta \omega \rangle = 0\). Sólo el segundo término sobrevive para un sistema con estadísticas gaussianas. Ahora reconociendo que tenemos un sistema estacionario, tenemos

\[F (t) = \exp \left[ - \frac {1} {2} \int _ {0}^{t} d \tau^{\prime} \, \int _ {0}^{t} d \tau^{\prime \prime} \, \left\langle \delta \omega \left( \tau^{\prime} - \tau^{\prime \prime} \right) \delta \omega ( 0 ) \right\rangle \right] \label{13.19}\]

Hemos reescrito la función de desfase n términos de una función de correlación que describe la brecha de energía fluctuante. Tenga en cuenta que esta es una excepción clásica, por lo que no hay ordenación del tiempo a lo exponencial. \(F(t)\)se puede reescribir a través de un cambio de variables (\(\tau = \tau^{\prime} - \tau^{\prime \prime}\)):

\[F (t) = \exp \left[ - \int _ {0}^{t} d \tau ( t - \tau ) \langle \delta \omega ( \tau ) \delta \omega ( 0 ) \rangle \right] \label{13.20}\]

Por lo que el modelo estocástico gaussiano permite describir la influencia de las fluctuaciones de frecuencia en la forma de línea mediante\(C _ {\delta \omega \delta v} (t)\) una función de correlación de frecuencia que sigue las estadísticas gaussianas. Tenga en cuenta, ahora estamos tratando con dos funciones de correlación diferentes\(C _ {\delta \omega \delta \omega}\) y\(C _ {\mu \mu}\). La función de correlación de frecuencia codifica la dinámica que resulta de moléculas que interactúan con el entorno, mientras que la función de correlación dipolo describe cómo interactúa el sistema con un campo de luz y con ello el espectro de absorción.

Ahora, calcularemos la forma de línea asumiendo que\(C _ {\delta \omega \delta \omega}\) decae con un tiempo de correlación\(\tau_c\) y toma una forma exponencial

\[C _ {\delta \omega \delta \omega} (t) = \Delta^{2} \exp \left[ - t / \tau _ {c} \right] \label{13.21}\]

Entonces la ecuación\ ref {13.20} da

\[F (t) = \exp \left[ - \Delta^{2} \tau _ {c}^{2} \left( \exp \left( - t / \tau _ {c} \right) + t / \tau _ {c} - 1 \right) \right] \label{13.22}\]

que está en la forma que hemos visto anteriormente\(F (t) = \exp ( - g (t) )\)

\[g (t) = \Delta^{2} \tau _ {c}^{2} \left( \exp \left( - t / \tau _ {c} \right) + t / \tau _ {c} - 1 \right) \label{13.23}\]

para interpretar esta función lineshape, veamos sus formas limitantes.

Tiempos de correlación largos (\( t \ll \tau_c\))

Esto corresponde al caso no homogéneo donde\(C _ {\delta \omega \delta \omega} (t) = \Delta^{2}\), una constante. Para\(t \ll \tau _ {c}\), podemos realizar una expansión de corto tiempo de exponencial

\[e^{- t / \tau _ {c}} \approx 1 - \frac {t} {\tau _ {c}} + \frac {t^{2}} {2 \tau _ {c}^{2}} + \ldots \label{13.24}\]

y de la Ecuación\ ref {13.23} obtenemos

\[g (t) = \Delta^{2} t^{2} / 2 \label{13.25}\]

En tiempos cortos, la función de correlación dipolo tendrá un decaimiento gaussiano con una tasa dada por\(\Delta^{2}\):

\[F (t) = \exp \left( - \Delta^{2} t^{2} / 2 \right)\]

Esto tiene el comportamiento adecuado para una función de correlación clásica, es decir, incluso en el tiempo

\[C _ {\mu \mu} (t) = C _ {\mu \mu} ( - t ).\]

En este límite, el lineshape de absorción es:

\[\begin{align} \sigma ( \omega ) & = | \mu |^{2} \int _ {- \infty}^{+ \infty} d t \, e^{i \omega t} e^{- i ( \omega ) t - g (t)} \\ & = | \mu |^{2} \int _ {- \infty}^{+ \infty} d t \, e^{i ( \omega - ( \omega ) ) t} e^{- \Delta^{2} t^{2} / 2} \\ & = \sqrt {\frac {2 \pi} {\Delta^{2}}} | \mu |^{2} \exp \left( - \frac {( \omega - \langle \omega \rangle )^{2}} {2 \Delta^{2}} \right) \label{13.26} \end{align}\]

Obtenemos un lineshape gaussiano no homogéneo centrado en la frecuencia media con un ancho dictado por la distribución de frecuencias.

Tiempos de correlación cortos (\( t \gg \tau_c\))

Esto corresponde al límite homogéneo en el que se puede aproximar

\[C _ {\delta \omega \delta \omega} (t) = \Delta^{2} \delta (t).\]

Para\(t \gg \tau _ {c}\) establecemos\(e^{- t / \tau _ {c}} \approx 0\),\(t / \tau _ {c} > > 1\), y la ecuación\ ref {13.23} da

\[g (t) = - \Delta^{2} \tau _ {c} t \label{13.27}\]

Si definimos la constante

\[\Delta^{2} \tau _ {c} \equiv \Gamma \label{13.28}\]

vemos que la función de desfase tiene un decaimiento exponencial:

\[F (t) = \exp [ - \Gamma t ] \label{13.29}\]

La forma de línea para tiempos de correlación cortos (o fluctuaciones rápidas) adquiere una forma lorentziana

\[ \begin{array} {c} {\sigma ( \omega ) = | \mu |^{2} \int _ {- \infty}^{+ \infty} d t \, e^{i ( \omega - \langle \omega ) t} e^{- \Gamma t}} \\ {\operatorname {Re} \sigma ( \omega ) = | \mu |^{2} \frac {\Gamma} {( \omega - \langle \omega \rangle )^{2} + \Gamma^{2}}} \end{array} \label{13.30}\]

Esto representa el límite homogéneo. Incluso con una amplia distribución de frecuencias accesibles, si el sistema explora todas estas frecuencias en una escala de tiempo rápida en comparación con la inversa de la distribución (\(\Delta \tau _ {\mathrm {c}} > 1\), entonces la resonancia se “estrechará mocionalmente” en una línea lorentziana.

De manera más general, la envolvente de la función de correlación dipolo se verá gaussiana en tiempos cortos y exponencial en tiempos largos.

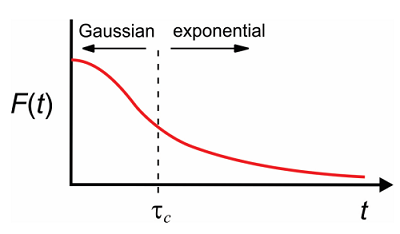
El tiempo de correlación es la separación entre estos regímenes. El comportamiento para escalas de tiempo variables de la dinámica (\(\tau_c\)) se caracteriza mejor con respecto a la distribución de frecuencias accesibles (\(\Delta\)). Así podemos definir un factor

\[\kappa = \Delta \cdot \tau _ {c} \label{13.31}\]

\(\kappa \ll 1\)es el límite de modulación rápida y\(\kappa \gg 1\) es el límite de modulación lenta. Veamos cómo\(C _ {\delta o \delta \omega}\),\(F (t)\), y\(\sigma _ {a b s} ( \omega )\) cambiar en función de\(\kappa\).

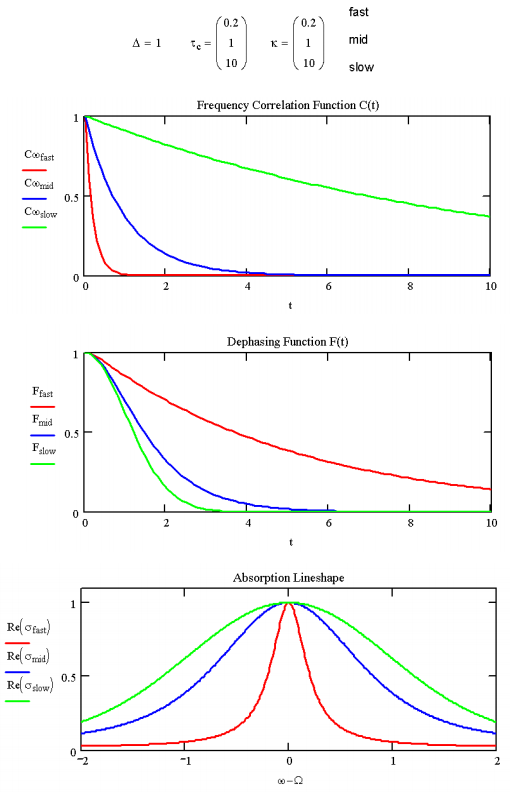
Vemos que para una distribución fija de frecuencias\(\Delta\) el efecto de aumentar la escala de tiempo de las fluctuaciones a través de esta distribución (decreciente\(\tau_c\)) es estrechar gradualmente la forma de línea observada de una distribución gaussiana de frecuencias estáticas con ancho (FWHM) de\(2.35\Delta\) a un mocionalmente estrechado Lorentzian lineshape con ancho (FWHM) de

\[\Delta^{2} \tau _ {c} / \pi = \Delta \cdot \kappa / \pi.\]

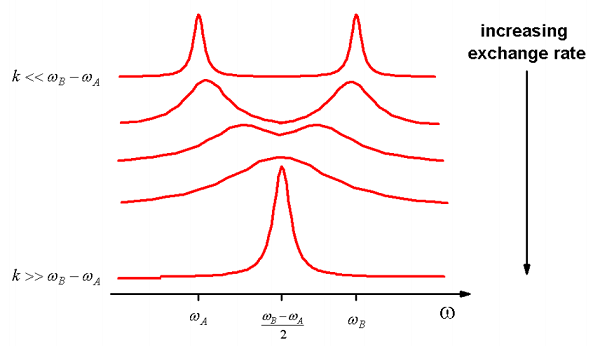
Esto es análogo al efecto de estrechamiento del movimiento descrito por primera vez en el caso de espectros de RMN dependientes de la temperatura de dos especies de intercambio. Supongamos que tenemos dos resonancias en\(\omega_A\) y\(\omega_B\) asociadas con dos especies químicas que están intercambiando a una velocidad\(k_{AB}\)

\[\ce{A <=> B}\]

Si la tasa de cambio es lenta en relación con la división de frecuencia,\(k _ {A B} < < \omega _ {A} - \omega B\) entonces se esperan dos resonancias, cada una con un ancho de línea dictado por los procesos de relajación molecular (\(T_2\)) y velocidad de transferencia de cada especie. Por otro lado, cuando la tasa de intercambio entre las dos especies se vuelve más rápida que la división de energía, entonces las dos resonancias se estrechan juntas para formar una resonancia a la frecuencia media.

Apéndice: La expansión acumulante

Para una descripción estadística de la variable aleatoria\(x\), deseamos caracterizar los momentos de\(x\):\(\langle x \rangle\),\(\langle x^2 \rangle\),... Entonces el promedio de un exponencial de se\(x\) puede expresar como una expansión en momentos

\[\underbrace{\left\langle e^{i k x} \right\rangle = \sum _ {n = 0}^{\infty} \frac {( i k )^n} {n !} \left\langle x^n \right\rangle}_{\text{expansion in moments}} \label{13.31A}\]

Una forma alternativa de expresar esta expansión es en términos de cumulantes

\[\underbrace{\left\langle e^{i k x} \right\rangle = \exp \left( \sum _ {n = 1}^{\infty} \frac {( i k )^{n}} {n !} c _ {n} (x) \right)}_{\text{expansion in cumulants}} \label{13.32}\]

donde los primeros acumulantes son:

\[ \begin{align} c _ {1} (x) &= \langle x \rangle \tag{mean} \label{13.33} \\[4pt] c _ {2} (x) &= \left\langle x^{2} \right\rangle - \langle x \rangle^{2} \label{13.34} \tag{variance} \\[4pt] c _ {3} (x) &= \left\langle x^{3} \right\rangle - 3 \langle x \rangle \left\langle x^{2} \right\rangle + 2 \langle x \rangle^{3} \tag{skewness} \label{13.35} \end{align}\]

Una expansión en acumulantes converge mucho más rápidamente que una expansión en momentos, particularmente cuando se considera que\(x\) puede ser una variable dependiente del tiempo. Particularmente útil es la observación de que todos los acumulantes con\(n > 2\) desaparecen para un sistema que obedece a las estadísticas gaussianas.

Obtenemos los acumulantes anteriores expandiendo la Ecuación\ ref {13.31} y\ ref {13.32}, y comparando términos en potencias de\(x\). Comenzamos postulando que, en lugar de expandir lo exponencial directamente, podemos expandir el argumento exponencial en potencias de un operador o variable\(H\)

\[F = \exp [ c ] = 1 + c + \frac {1} {2} c^{2} + \cdots \label{13.36}\]

\[c = c _ {1} H + \frac {1} {2} c _ {2} H^{2} + \cdots \label{13.37}\]

Insertando la ecuación\ ref {13.37} en la ecuación\ ref {13.36} y recogiendo términos en órdenes de\(H\) da

\[\begin{aligned} F & = 1 + \left( c _ {1} H + \frac {1} {2} c _ {2} H^{2} + \cdots \right) + \frac {1} {2} \left( c _ {1} H + \frac {1} {2} c _ {2} H^{2} + \cdots \right)^{2} + \cdots \\ & = 1 + \left( c _ {1} \right) H + \frac {1} {2} \left( c _ {2} + c _ {1}^{2} \right) H^{2} + \cdots \end{aligned} \label{13.38}\]

Ahora comparando esto con la expansión del operador exponencial (de\(H\))

\[\begin{align} F & = \exp [ f H ] \\ & = 1 + f _ {1} H + \frac {1} {2} f _ {2} H^{2} + \cdots \label{13.39} \end{align}\]

permite que uno vea que

\[\begin{array} {l} {c _ {1} = f _ {1}} \\ {c _ {2} = f _ {2} - f _ {1}^{2}} \end{array} \label{13.40}\]

La expansión acumulante también se puede aplicar a correlaciones de tiempo. Aplicando esto al operador exponencial ordenado por tiempo obtenemos:

\[\begin{align} F (t) & = \left\langle \exp _ {+} \left[ - i \int _ {0}^{t} d t \omega (t) \right] \right\rangle \\ & \approx \exp \left[ c _ {1} (t) + c _ {2} (t) \right] \label{13.42} \end{align} \]

\[\begin{aligned} c _ {1} & = - i \int _ {0}^{t} d \tau \langle \omega ( \tau ) \rangle \\ c _ {2} & = - \int _ {0}^{t} d \tau _ {2} \int _ {0}^{\tau _ {2}} d \tau _ {1} \left\{\left\langle \omega \left( \tau _ {2} \right) \omega \left( \tau _ {1} \right) \right\rangle - \left\langle \omega \left( \tau _ {2} \right) \right\rangle \left\langle \omega \left( \tau _ {1} \right) \right\rangle \right\} \\ & = - \int _ {0}^{t} d \tau _ {2} \int _ {0}^{\tau _ {2}} d \tau _ {1} \left\langle \delta \omega \left( \tau _ {2} \right) \delta \omega \left( \tau _ {1} \right) \right\rangle \end{aligned} \label{13.43}\]

Para las estadísticas gaussianas, todos los acumulantes superiores desaparecen.

Lecturas

1. Kubo, R., Una teoría estocástica de la forma de línea y la relajación. En Fluctuación, Relajación y Resonancia en Sistemas Magnéticos, Ter Haar, D., Ed. Oliver y Boyd: Edimburgo, 1962; pp 23- 68.
2. McHale, J. L., Espectroscopia Molecular. 1a ed.; Prentice Hall: Upper Saddle River, NJ, 1999.
3. Mukamel, S., Principios de Espectroscopia Óptica No Lineal. Oxford University Press: Nueva York, 1995.
4. Schatz, G. C.; Ratner, M. A., Mecánica Cuántica en Química. Publicaciones de Dover: Mineola, NY, 2002; Secciones 7.4 y 7.5.
5. W. Anderson, P., Un modelo matemático para el estrechamiento de líneas espectrales por intercambio o movimiento. Revista de la Sociedad Física de Japón 1954, 9, 316-339.
6. Wang, C. H., Espectroscopia de Medios Condensados: Dinámica de Interacciones Moleculares. Prensa Académica: Orlando, 1985.