14.4: La brecha energética hamiltoniana

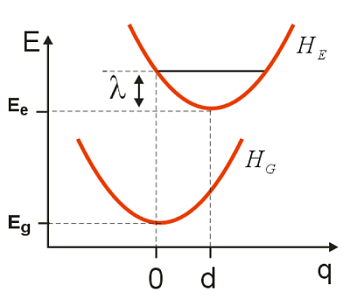
Al describir las fluctuaciones en un sistema mecánico cuántico, describimos cómo un observable experimental es influenciado por sus interacciones con un ambiente agitado térmicamente. Para ello, se trabaja con el ejemplo específico de un espectro electrónico de absorción y retorno al modelo de Oscilador Armónico Desplazado (DHO). Anteriormente describimos este modelo en términos de los estados propios del material Hamiltoniano\(H_0\), e interpretamos la función de correlación dipolo y la forma de línea resultante en términos de la superposición entre dos paquetes de ondas que evolucionan sobre el suelo y superficies excitadas\(| E \rangle\) y\(| G \rangle\).

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \left( E _ {e} - E _ {g} \right) t / \hbar} \left\langle \varphi _ {g} (t) | \varphi _ {e} (t) \right\rangle \label{13.43}\]

Cabe destacar una similitud entre el DHO Hamiltoniano, y una forma general para la interacción de un “sistema” electrónico de dos niveles con un oscilador armónico “baño” cuyos grados de libertad son oscuros a la observación, pero que influyen en el comportamiento del sistema.

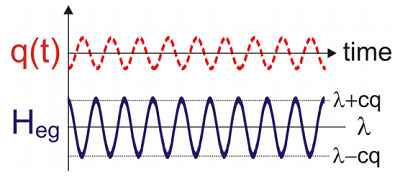
Expresado en una imagen física ligeramente diferente, también podemos concebir este proceso como movimientos nucleares que actúan para modular la brecha de energía electrónica\(\omega _ {e g}\). Podemos imaginar reescribir el mismo hamiltoniano en una forma con una nueva imagen física que describe la dependencia de la brecha de energía electrónica de\(q\), es decir, su variación relativa a\(\omega _ {e g}\). Si definimos una Brecha Energética Hamiltoniana:

\[H _ {e g} = H _ {e} - H _ {g}\]

podemos reescribir el DHO Hamiltoniano

\[H _ {0} = | e \rangle E _ {e} \langle e | + | g \rangle E _ {g} \langle g | + H _ {e} + H _ {g} \label{13.44}\]

como una transición electrónica acoplada linealmente a un oscilador armónico:

\[H _ {0} = | e \rangle E _ {e} \langle e | + | g \rangle E _ {g} \langle g | + H _ {e g} + 2 H _ {g} \label{13.44B}\]

Señalando que

\[H _ {g} = \frac {p^{2}} {2 m} + \frac {1} {2} m \omega _ {0}^{2} q^{2} \label{13.44C}\]

podemos escribir esto como un hamiltoniano sistema-baño:

\[H _ {0} = H _ {S} + H _ {B} + H _ {S B} \label{13.44D}\]

donde se\(H_{SB}\) describe la interacción del sistema electrónico (\(H_S\)) con el baño vibratorio (\(H_B\)). Aquí

\[H _ {S} = | e \rangle E _ {e} \langle e | + | g \rangle E _ {g} \langle g |\]

\[H _ {B} = 2 H _ {g}\]

y

\[\begin{align} H _ {S B} = H _ {e g} &= \dfrac {1} {2} m \omega _ {0}^{2} ( q - d )^{2} - \frac {1} {2} m \omega _ {0}^{2} q^{2} \\ &= - m \omega _ {0}^{2} d q + \frac {1} {2} m \omega _ {0}^{2} d^{2} \\ &= - c q + \lambda \end{align}\]

El Hamiltoniano Energy Gap describe un acoplamiento lineal entre la transición electrónica y un oscilador armónico. La fuerza del acoplamiento es\(c\) y el hamiltoniano tiene un valor de compensación de energía constante dado por la energía de reorganización (\(\lambda\)). Cualquier movimiento en la coordenada del baño\(q\) introduce un cambio proporcional en la brecha de energía electrónica.

En una forma alternativa, la Brecha de Energía Hamiltoniana también se puede escribir para incorporar la energía de reorganización al sistema:

\[\begin{align*} H _ {0} &= | e \rangle E _ {e} \langle e | + | g \rangle E _ {g} \langle g | + H _ {e g} + 2 H _ {g} \label{13.44E} \\[4pt] H _ {S}^{\prime} &= | e \rangle \left( E _ {e} + \lambda \right) \langle e | + | g \rangle E _ {g} \langle g | \\[4pt] H _ {B}^{\prime} &= \frac {p^{2}} {2 m} + \frac {1} {2} m \omega _ {0}^{2} q^{2} \\[4pt] H _ {S B}^{\prime} &= - m \omega _ {0}^{2} d q \end{align*}\]

Esta formulación describe fluctuaciones sobre el valor promedio de la brecha energética\(\hbar \omega _ {e g} + \lambda\), sin embargo, los observables calculados son los mismos.

A partir de la imagen de una brecha de energía modulada se puede comenzar a ver cómo se pueden tratar las fluctuaciones aleatorias acoplándose a un baño armónico. Si cada oscilador modula la brecha de energía a una frecuencia dada, y la fase entre los osciladores es aleatoria como resultado de su independencia, entonces las fluctuaciones en el dominio del tiempo y la desfase se pueden emitir en términos de un espectro de Fourier de acoplamientos a osciladores con frecuencia continuamente variable.

Brecha Energética Hamiltoniana

Ahora trabajemos a través de la descripción de la espectroscopia electrónica con el Hamiltoniano Energy Gap con más cuidado. Trabajando a partir de las ecuaciones\ ref {13.43} y\ ref {13.44} expresamos la brecha de energía hamiltoniana a través de coordenadas reducidas para el impulso, la coordenada y el desplazamiento del oscilador.

\[p = \hat {p} \left( 2 \hbar \omega _ {0} m \right)^{- 1 / 2}\]

\[q = \hat {q} \left( m \omega _ {0} / 2 \hbar \right)^{1 / 2}\]

\[d = d \left( m \omega _ {0} / 2 \hbar \right)^{1 / 2}\]

con

\[ \begin{align} H _ {e} &= \hbar \omega _ {0} \left( p^{2} + ( q - d )^{2} \right) \\[4pt] H_{g} &= \hbar \omega _ {0} \left( p^{2} + q^{2} \right) \end{align} \label{13.48}\]

De la Ecuación\ ref {13.43} tenemos

\[\left.\begin{aligned} H _ {e g} & = - 2 \hbar \omega _ {0} d q + \hbar \omega _ {0} d^{2} \\ & = - m \omega _ {0}^{2} d q + \lambda \end{aligned} \right. \label{13.49}\]

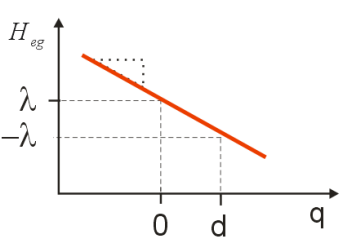
La brecha de energía Hamiltoniano describe un acoplamiento lineal del sistema electrónico a la coordenada q. La pendiente de\(H_{eg}\) versus\(q\) es la fuerza de acoplamiento, y el valor promedio de\(H_{eg}\) en el estado fundamental,\(H _ {e g} ( q = 0 )\), está compensado por la energía de reorganización\(\lambda\). Observamos que el valor promedio de la brecha energética hamiltoniana es\(\left\langle H _ {e g} \right\rangle = \lambda\).

Para obtener la forma de línea de absorción a partir de la función de correlación dipolo

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \omega _ {e g} t} F (t) \label{13.50}\]

debemos evaluar la función de desfase.

\[F (t) = \left\langle e^{i H _ {g} t} e^{- i H _ {e} t} \right\rangle = \left\langle U _ {g}^{\dagger} U _ {e} \right\rangle \label{13.51}\]

Queremos reescribir la función de desfase en términos de la dependencia del tiempo a la brecha energética\(H_{eg}\); es decir, si\(F (t) = \left\langle U _ {c g} \right\rangle\), entonces ¿qué es\(U _ {e g}\)? Esto implica una transformación unitaria de la dinámica a un nuevo marco de referencia. La transformación del DHO Hamiltoniano al EG Hamiltoniano es similar a nuestra derivación de la imagen de interacción.

Transformación de propagadores de tiempo

Si tenemos una cantidad dependiente del tiempo del formulario

\[e^{i H _ {A} t} A e^{- i H _ {B} t} \label{13.52}\]

también podemos expresar la dinámica a través de la diferencia hamiltoniana\(H _ {B A} = H _ {B} - H _ {A}\)

\[A e^{- i \left( H _ {B} - H _ {A} \right) t} = A e^{- i H _ {B A} t} \label{13.53}\]

utilizando una transformación unitaria comúnmente realizada. Si escribimos

\[H _ {B} = H _ {A} + H _ {B A} \label{13.54}\]

podemos usar el mismo procedimiento para particionar la dinámica en la imagen de interacción para escribir

\[e^{- i H _ {B t} t} = e^{- i H _ {A} t} \exp _ {+} \left[ - \frac {i} {\hbar} \int _ {0}^{t} d \tau H _ {B A} ( \tau ) \right] \label{13.55}\]

donde

\[H _ {B A} ( \tau ) = e^{i H _ {A} t} H _ {B A} e^{- i H _ {A} t} \label{13.56}\]

Entonces, también podemos escribir:

\[e^{i H _ {A} t} e^{- i H _ {B} t} = \exp _ {+} \left[ - \frac {i} {\hbar} \int _ {0}^{t} d \tau H _ {B A} ( \tau ) \right] \label{13.57}\]

Observando el mapeo a la imagen de interacción

\[H _ {e} = H _ {g} + H _ {e g} \quad \Leftrightarrow \quad H = H _ {0} + V \label{13.58}\]

vemos que podemos representar la dependencia temporal de la brecha de energía electrónica\(H_{eg}\) utilizando

\[e^{- i H _ {c} t / h} = e^{- i H _ {g} t / h} \exp _ {+} \left[ \frac {- i} {\hbar} \int _ {0}^{t} d \tau H _ {e g} ( \tau ) \right] \label{13.59}\]

\[U _ {e} = U _ {g} U _ {e g}\]

donde

\[\begin{align} H _ {e g} (t) & = e^{i H _ {g} t / \hbar} H _ {e g} e^{- i H _ {g} t / \hbar} \\ & = U _ {g}^{\dagger} H _ {e g} U _ {g} \label{13.60} \end{align} \]

Recordar la equivalencia entre el modo armónico\(H_g\) y el modo (s) de baño\(H_B\) indica que la dependencia del tiempo del EG Hamiltoniano refleja cómo se modula la brecha de energía electrónica como resultado de las interacciones con el baño. Eso es\(U _ {g} \Leftrightarrow U _ {B}\).

La ecuación\ ref {13.59} implica inmediatamente que

\[F (t) = \left\langle e^{i H _ {g} t / \hbar} e^{- i H _ {e} t / \hbar} \right\rangle = \left\langle \exp _ {+} \left[ \frac {- i} {\hbar} \int _ {0}^{t} d \tau H _ {e g} ( \tau ) \right] \right\rangle \label{13.61}\]

Ahora la función de desfase cuántica está en la misma forma que vimos en nuestra derivación clásica anterior. El uso de la expansión acumulante de segundo orden permite que la función de desfase se escriba como

\[F (t) = \left\langle e^{i H _ {g} t / \hbar} e^{- i H _ {e} t / \hbar} \right\rangle = \left\langle \exp _ {+} \left[ \frac {- i} {\hbar} \int _ {0}^{t} d \tau H _ {e g} ( \tau ) \right] \right\rangle \label{13.62}\]

Tenga en cuenta que la expansión acumulante se escribe aquí como una expansión ordenada por tiempo. El primer término exponencial depende del valor medio de\(H_{eg}\)

\[\left\langle H _ {e g} \right\rangle = \hbar \omega _ {0} d^{2} = \lambda \label{13.63}\]

Esto es resultado de cómo definimos\(H_{eg}\). Alternativamente, el EG Hamiltoniano podría haberse definido en relación con la brecha de energía en\(Q=0\):\(H _ {e g} = H _ {e} - H _ {g} + \lambda\). En este caso el término principal en la Ecuación\ ref {13.62} sería cero, y la brecha de energía media que describe la oscilación de alta frecuencia (sistema) en la función de correlación dipolo es\(\omega _ {e g} + \lambda\).

El segundo término exponencial en la Ecuación\ ref {13.62} es una función de correlación que describe la dependencia temporal de la brecha de energía

\[\left. \begin{array} {c} {\left\langle H _ {e g} \left( \tau _ {2} \right) H _ {e g} \left( \tau _ {1} \right) \right\rangle - \left\langle H _ {e g} \left( \tau _ {2} \right) \right\rangle \left\langle H _ {e g} \left( \tau _ {1} \right) \right\rangle} \\ {= \left\langle \delta H _ {e g} \left( \tau _ {2} \right) \delta H _ {e g} \left( \tau _ {1} \right) \right\rangle} \end{array} \right. \label{13.64}\]

donde

\[\left.\begin{aligned} \delta H _ {e g} & = H _ {e g} - \left\langle H _ {e g} \right\rangle \\ & = - m \omega _ {0}^{2} d q \end{aligned} \right. \label{13.65}\]

Definición de la frecuencia de transición de brecha energética dependiente del tiempo en términos del EG Hamiltoniano como

\[\delta \hat {\omega} _ {e g} \equiv \frac {\delta H _ {e g}} {\hbar} \label{13.66}\]

podemos escribir la función de correlación de brecha de energía

\[C _ {e g} \left( \tau _ {2} , \tau _ {1} \right) = \left\langle \delta \hat {\omega} _ {e g} \left( \tau _ {2} - \tau _ {1} \right) \delta \hat {\omega} _ {e g} ( 0 ) \right\rangle \label{13.68}\]

De ello se deduce que

\[F (t) = e^{- i \lambda t / \hbar} e^{- g (t)}\]

y

\[g (t) = \int _ {0}^{t} d \tau _ {2} \int _ {0}^{\tau _ {2}} d \tau _ {1} C _ {e g} \left( \tau _ {2} , \tau _ {1} \right) \label{13.69}\]

y la función de correlación dipolo se puede expresar como

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \left( E _ {e} - E _ {g} + \lambda \right) t / \hbar} e^{- g (t)} \label{13.70}\]

Esta es la expresión de la función de correlación que determina la forma de línea de absorción para una brecha de energía dependiente del tiempo. Es una expresión general en este punto, para todas las formas de la función de correlación de brecha de energía. La única aproximación hecha para el baño es la segunda expansión acumulante.

Ahora, veamos específicamente el caso en el que el baño al que estamos acoplados es un modo de armónico único. La función de correlación de brecha de energía se evalúa a partir de

\[\left.\begin{aligned} C _ {e g} (t) & = \sum _ {n} p _ {n} \left\langle n \left| \delta \hat {\omega} _ {e g} (t) \delta \hat {\omega} _ {e g} ( 0 ) \right| n \right\rangle \\ & = \frac {1} {\hbar^{2}} \sum _ {n} p _ {n} \left\langle n \left| e^{i H _ {g} t / \hbar} \delta H _ {e g} e^{- i H _ {g} t / \hbar} \delta H _ {e g} \right| n \right\rangle \end{aligned} \right. \label{13.71}\]

Observando que la función de correlación del oscilador de baño

\[C _ {q q} (t) = \langle q (t) q ( 0 ) \rangle = \frac {\hbar} {2 m \omega _ {0}} \left[ ( \overline {n} + 1 ) e^{- i \omega _ {0} t} + \overline {n} e^{i \omega _ {0} t} \right] \label{13.72}\]

encontramos

\[C _ {e g} (t) = \omega _ {0}^{2} D \left[ ( \overline {n} + 1 ) e^{- i \omega _ {0} t} + \overline {n} e^{i \omega _ {0} t} \right] \label{13.73}\]

Aquí, como antes\(\beta = 1 / k _ {B} T\),\(\overline {n}\) está el número de ocupación promediado térmicamente para el oscilador

\[\overline {n} = \sum _ {n} p _ {n} \left\langle n \left| a^{\dagger} a \right| n \right\rangle = \left( e^{\beta \hbar \omega _ {b}} - 1 \right)^{- 1} \label{13.74}\]

y\(\beta = 1 / \mathrm {kB} \mathrm {T}\). Tenga en cuenta que la función de correlación de brecha de energía es una función compleja. Podemos separar las partes reales e imaginarias de\(C_{eg}\) como

\[C _ {e g} (t) = C _ {e g}^{\prime} + i C _ {e g}^{\prime \prime} \label{13.75}\]

con

\[\begin{align} C _ {e g}^{\prime} (t) &= \omega _ {0}^{2} D \operatorname {coth} \left( \beta \hbar \omega _ {0} / 2 \right) \cos \left( \omega _ {0} t \right) \\[4pt] C _ {e g}^{\prime \prime} (t) &= \omega _ {0}^{2} D \sin \left( \omega _ {0} t \right) \end{align} \label{13.76}\]

donde hemos hecho uso de la relación

\[2 \overline {n} ( \omega ) + 1 = \operatorname {coth} ( \beta \hbar \omega / 2 ) \label{13.77}\]

y

\[\operatorname{coth}(x)=\left(e^{x}+e^{-x}\right) /\left(e^{x}-e^{-x}\right)\]

Vemos que la parte imaginaria de la función de correlación de brecha de energía es independiente de la temperatura. La parte real tiene la misma amplitud a\(T=0\), y se eleva con la temperatura. Podemos analizar los límites de temperatura alta y baja de esta expresión desde

\[\begin{align} \lim_{x \rightarrow \infty} \operatorname {coth} (x) = 1 \\[4pt] \lim_{x \rightarrow 0} \operatorname {coth} (x) \approx \frac {1} {x} \end{align} \label{13.78}\]

Mirando el límite de temperatura baja\(\operatorname{coth}\left(\beta \hbar \omega_{0} / 2\right) \rightarrow 1\) y\(\overline {n} \rightarrow 0\) vemos que la Ecuación\ ref {13.82} reduce a la Ecuación\ ref {13.84}.

En el límite de temperatura alta\(k T > \star \omega _ {0}\),\(\operatorname {coth} \left( \hbar \omega _ {0} / 2 k T \right) \rightarrow 2 k T / \hbar \omega _ {0}\) y recuperamos el resultado clásico esperado. La magnitud del componente real domina la parte imaginaria\(\left| C _ {e g}^{\prime} \right| > > \left| C _ {e g}^{\prime \prime} \right|\) y la función de correlación de brecha de energía (\(C_{eq}(t)\)se vuelve real e incluso en el tiempo.

Del mismo modo, podemos evaluar la ecuación\ ref {13.69}, la función lineshape

\[g (t) = - D \left[ ( \overline {n} + 1 ) \left( e^{- i \omega _ {0} t} - 1 \right) + \overline {n} \left( e^{i \omega _ {0} t} - 1 \right) \right] - i D \omega _ {0} t \label{13.79}\]

El término principal en la Ecuación\ ref {13.79} nos da una progresión vibracional, el segundo término conduce a bandas calientes, y el término final es la energía de reorganización (\(- i D \omega _ {0} t = - i \lambda t / \hbar\)). La función lineshape se puede escribir en términos de sus partes reales e imaginarias

\[g(t)=g^{\prime}+i g^{\prime \prime}\]

con

\[\begin{align} g^{\prime} (t) &= D \operatorname {coth} \left( \beta \hbar \omega _ {0} / 2 \right) \left( 1 - \cos \omega _ {0} t \right) \\[4pt] g^{\prime \prime} (t) &= D \left( \sin \omega _ {0} t - \omega _ {0} t \right) \label{13.81} \end{align}\]

Debido a que estos entran en la función de correlación dipolo como argumentos exponenciales, la parte imaginaria de\(g(t)\) reflejará el cambio de energía inducido por el baño de la brecha de transición electrónica y la estructura vibrónica, y la parte real reflejará la amortiguación, y por lo tanto la ampliación de la forma de línea. De manera similar a\(C_{eg}(t)\), en el límite de temperatura alta\(g' \gg g''\). Ahora, usando la ecuación\ ref {13.68}, vemos que la función de desfase viene dada por

\ [\ begin {align} F (t) &=\ exp\ izquierda [D\ izquierda ((\ bar {n} +1)\ izquierda (e^ {-i\ omega_ {0} t} -1\ derecha) +\ bar {n}\ izquierda (e^ {i\ omega_ {0} t} -1\ derecha)\ derecha)\ derecha]\\ [4pt]
&=\ exp izquierda\ [D\ izquierda (\ nombreoperador {coth}\ izquierda (\ frac {\ beta\ hbar\ omega} {2}\ derecha) (1-\ cos\ omega t) +i\ sin\ omega t\ derecha)\ derecha]\ end {align}\ etiqueta {13.82}\]

Confirmemos que obtenemos el mismo resultado que con nuestro modelo DHO original, cuando tomamos el límite de temperatura baja. Estableciendo\(\overline {n} \rightarrow 0\) en Ecuación\ ref {13.82}, tenemos nuestro resultado original

\[F_{k T=0}(t)=\exp \left[D\left(e^{-i \omega_{0} t}-1\right)\right]\label{13.84}\]

En el límite de temperatura alta\(g' \gg g''\), y de la Ecuación\ ref {13.78} obtenemos

\[\left.\begin{aligned} F (t) & = \exp \left[ \frac {2 D k T} {\hbar \omega _ {0}} \cos \left( \omega _ {0} t \right) \right] \\ & = \sum _ {j = 0}^{\infty} \frac {1} {j !} \left( \frac {2 D k T} {\hbar \omega _ {0}} \right)^{j} \cos^{j} \left( \omega _ {0} t \right) \end{aligned} \right. \label{13.85}\]

lo que conduce a un espectro de absorción que es una serie de bandas laterales igualmente espaciadas a cada lado de\(\text {oleg}\).

Representación espectral de la función de correlación de brecha energética

Dado que las representaciones en el dominio del tiempo y la frecuencia son complementarias, y una forma puede ser preferible sobre otra, es posible expresar la función de correlación de frecuencia en términos de su espectro. Para un espectro complejo de movimientos vibracionales compuesto por muchos modos, representar los movimientos nucleares en términos de un espectro en lugar de un patrón de latidos suele ser más fácil. Resulta que los cálculos suelen ser más fáciles de realizar en el dominio de la frecuencia. Para comenzar definimos un par de transformada de Fourier que relaciona las representaciones de dominio de tiempo y frecuencia:

\[\tilde {C} _ {e g} ( \omega ) = \int _ {- \infty}^{+ \infty} e^{i \omega t} C _ {e g} (t) d t \label{13.86}\]

\[C _ {e g} (t) = \frac {1} {2 \pi} \int _ {- \infty}^{+ \infty} e^{- i \omega t} \tilde {C} _ {e g} ( \omega ) d \omega \label{13.87}\]

Dado que la función de correlación de brecha de energía tiene la propiedad

\[C _ {e g} ( - t ) = C _ {e g}^{*} (t)\]

también se deduce de la Ecuación\ ref {13.86} que el espectro de correlación de brecha de energía es completamente real:

\[\tilde {C} _ {e g} ( \omega ) = 2 \operatorname {Re} \int _ {0}^{\infty} e^{i \omega t} C _ {e g} (t) d t \label{13.88}\]

o

\[\tilde {C} _ {e g} ( \omega ) = \tilde {C} _ {e g}^{\prime} ( \omega ) + \tilde {C} _ {e g}^{\prime \prime} ( \omega ) \label{13.89}\]

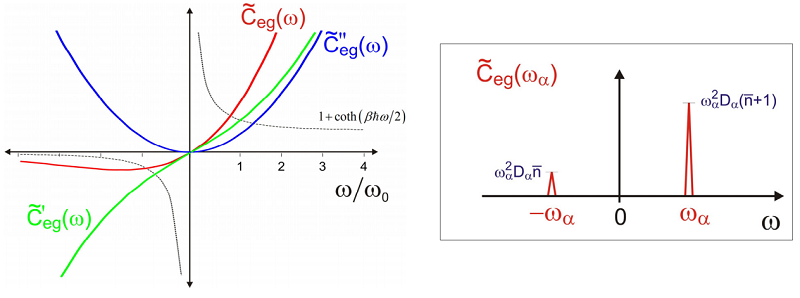
Aquí\(\tilde {C} _ {e s}^{\prime} ( \omega )\) y\(\tilde {C} _ {e g}^{\prime \prime} ( \omega )\) están las transformaciones de Fourier de los componentes real e imaginario de\(C _ {e s} (t)\), respectivamente. \(\tilde {C} _ {e s}^{\prime} ( \omega )\)y\(\tilde {C} _ {e g}^{\prime \prime} ( \omega )\) son pares e impares en frecuencia. Así, si bien\(\tilde {C} _ {e s} ( \omega )\) es totalmente real valorado, es asimétrico sobre\(\omega = 0\).

Con estas definiciones en la mano, podemos escribir el espectro de la función de correlación de brecha de energía para acoplarse a un espectro de modo armónico único (Ecuación\ ref {13.71}):

\[\tilde {C} _ {e g} \left( \omega _ {\alpha} \right) = \omega _ {\alpha}^{2} D \left( \omega _ {\alpha} \right) \left[ \left( \overline {n} _ {\alpha} + 1 \right) \delta \left( \omega - \omega _ {\alpha} \right) + \overline {n} _ {\alpha} \delta \left( \omega + \omega _ {\alpha} \right) \right] \label{13.90}\]

Se trata de un espectro que caracteriza cómo actúan los modos vibratorios de baño de cierta frecuencia y ocupación térmica para modificar la energía observada del sistema. El primer y segundo términos en la Ecuación\ ref {13.90} describen los desplazamientos de energía hacia arriba y hacia abajo del sistema, respectivamente. El acoplamiento a una vibración generalmente conduce a un cambio ascendente de la energía de transición de brecha de energía, ya que la energía debe ser puesta en el sistema y el baño. Sin embargo, al igual que con las bandas calientes, cuando hay energía térmica disponible en el baño, también permite cambios descendentes en la brecha de energía. El saldo neto de los desplazamientos ascendentes y descendentes promediados sobre el baño sigue la expresión detallada del balance

\[\tilde {C} ( - \omega ) = e^{- \beta \hbar \omega} \tilde {C} ( \omega ) \label{13.91}\]

El balance de tasas tiende a ser igual con el aumento de la temperatura. Las transformaciones de Fourier de la Ecuación\ ref13.76} dan otras dos representaciones del espectro de brecha de energía

\[\tilde {C} _ {e g}^{\prime} \left( \omega _ {\alpha} \right) = \omega _ {\alpha}^{2} D \left( \omega _ {\alpha} \right) \operatorname {coth} \left( \beta \hbar \omega _ {\alpha} / 2 \right) \left[ \delta \left( \omega - \omega _ {\alpha} \right) + \delta \left( \omega + \omega _ {\alpha} \right) \right] \label{13.92}\]

\[\tilde {C} _ {e g}^{\prime \prime} \left( \omega _ {\alpha} \right) = \omega _ {\alpha}^{2} D \left( \omega _ {\alpha} \right) \left[ \delta \left( \omega - \omega _ {\alpha} \right) + \delta \left( \omega + \omega _ {\alpha} \right) \right]. \label{13.93}\]

Las representaciones en la Ecuación\ ref {13.90},\ ref {13.92}, y\ ref {13.93} no son independientes, sino que pueden relacionarse entre sí a través de

\[\tilde{C}_{e g}^{\prime}\left(\omega_{\alpha}\right)=\operatorname{coth}\left(\beta \hbar \omega_{\alpha} / 2\right) \tilde{C}_{e g}^{\prime \prime}\left(\omega_{\alpha}\right)\]

\[\tilde {C} _ {e g} \left( \omega _ {\alpha} \right) = \left( 1 + \operatorname {coth} \left( \beta \hbar \omega _ {\alpha} / 2 \right) \right) \tilde {C} _ {e g}^{\prime \prime} \left( \omega _ {\alpha} \right) \label{13.95}\]

Es decir, dada la parte real o imaginaria del espectro de correlación de brecha energética, podemos predecir la otra parte. Como veremos, esta relación es una manifestación del teorema de fluctuacióndisipación que abordaremos más adelante. Debido a su independencia sobre la temperatura, la densidad espectral\(\tilde {C} _ {e g}^{\prime \prime} \left( \omega _ {\alpha} \right)\) es la representación comúnmente utilizada.

También de Ecuaciones. \ ref {13.69} y\ ref {13.87} obtenemos la función lineshape como

\[\left.\begin{aligned} g (t) & = \int _ {- \infty}^{+ \infty} d \omega \frac {1} {2 \pi} \frac {\tilde {C} _ {e g} ( \omega )} {\omega^{2}} [ \exp ( - i \omega t ) + i \omega t - 1 ] \\ & = \int _ {0}^{\infty} d \omega \frac {\tilde {C} _ {e g}^{\prime \prime} ( \omega )} {\pi \omega^{2}} \left[ \operatorname {coth} \left( \frac {\beta \hbar \omega} {2} \right) ( 1 - \cos \omega t ) + i ( \sin \omega t - \omega t ) \right] \end{aligned} \right. \label{13.96}\]

La primera expresión relaciona g (t) con la función de correlación de brecha de energía compleja, mientras que la segunda separa las partes real e imaginaria y las relaciona con la parte imaginaria de la función de correlación de brecha de energía.

Acoplamiento a un baño armónico

Más generalmente para problemas de fase condensada, las coordenadas del sistema que observamos en un experimento interactuarán con un continuo de movimientos nucleares que pueden reflejar vibraciones moleculares, fonones o interacciones intermoleculares. Describimos este continuo como distribución continua de osciladores armónicos de frecuencia de modo variable y fuerza de acoplamiento. La Brecha de Energía Hamiltoniana se generaliza fácilmente al caso de una distribución continua de movimientos si caracterizamos estadísticamente la densidad de estados y la fuerza de interacción entre el sistema y este baño. Este método también se conoce como el Modelo Spin-Boson utilizado para tratar un sistema spin-½ de dos niveles que interactúa con un baño armónico cuántico.

Siguiendo nuestra anterior discusión sobre el modelo DHO, la generalización del EG Hamiltoniano al caso multimodo es

\[H _ {0} = \hbar \omega _ {e g} + H _ {e g} + H _ {B} \label{13.97}\]

\[H _ {B} = \sum _ {\alpha} \hbar \omega _ {\alpha} \left( p _ {\sim}^{2} + q _ {\alpha}^{2} \right) \label{13.98}\]

\[H _ {e g} = \sum _ {\alpha} 2 \hbar \omega _ {\alpha} d _ {\alpha} q _ {\alpha} + \lambda \label{13.99}\]

\[\lambda = \sum _ {\alpha} \hbar \omega _ {\alpha} d _ {\alpha}^{2} \label{13.100}\]

Tenga en cuenta que la dependencia del tiempo a\(H_{eg}\) los resultados de la interacción con el baño:

\[H _ {e g} (t) = e^{i H _ {B} t / \hbar} H _ {e g} e^{- i H _ {B} t / \hbar} \label{13.101}\]

Además, dado que los modos armónicos son normales entre sí, la función de desfase y la función de forma de línea se obtienen de la ecuación\ ref {13.102}

\[F(t)=\prod_{\alpha} F_{\alpha}(t) \quad g(t)=\sum_{\alpha} g_{\alpha}(t)\label{13.102}\]

Para un continuo, asumimos que el número de modos es tan numeroso como para ser continuo, y que las sumas en las ecuaciones anteriores pueden ser reemplazadas por integrales sobre una distribución continua de estados caracterizada por una densidad de estados W Z. También la interacción con modos de una frecuencia particular son iguales de manera que simplemente podemos promediar sobre una constante de acoplamiento dependiente de la frecuencia 2 D d Z Z Z. Por ejemplo, la ecuación\ ref {13.102} se convierte

\[g (t) = \int d \omega _ {\alpha} W \left( \omega _ {\alpha} \right) g \left( t , \omega _ {\alpha} \right) \label{13.103}\]

El acoplamiento a un continuo conduce a la desfase resultante de la interacción a un continuo de modos de frecuencia variable. Esto se caracterizará por la amortiguación de la función de correlación de frecuencia de brecha de energía

\[C _ {e g} (t) = \int d \omega _ {\alpha} C _ {e g} \left( \omega _ {\alpha} , t \right) W \left( \omega _ {\alpha} \right) \label{13.104}\]

Aquí\(C _ {e g} \left( \omega _ {\alpha} , t \right) = \left\langle \delta \omega _ {e g} \left( \omega _ {\alpha} , t \right) \delta \omega _ {e g} \left( \omega _ {\alpha} , 0 \right) \right\rangle\) se refiere a la función de correlación de frecuencia de brecha de energía para un modo armónico único dada en la Ecuación\ ref {13.71}. Mientras que la Ecuación\ ref {13.104} expresa la modulación de la brecha de energía en el dominio del tiempo, alternativamente podemos expresar la distribución continua de los modos de baño acoplados en el dominio de la frecuencia:

\[\tilde {C} _ {e g} ( \omega ) = \int d \omega _ {\alpha} W \left( \omega _ {\alpha} \right) \tilde {C} _ {e g} \left( \omega _ {\alpha} \right) \label{13.105}\]

Una integral de un espectro de modo armónico único sobre una densidad continua de estados proporciona una densidad ponderada de acoplamiento de estados que refleja el espectro de acción para la interacción sistema-baño. Esto se evalúa con el espectro de modo armónico único, Ecuación\ ref {13.90}. Vemos que el espectro de la función de correlación para frecuencias positivas está relacionado con el producto de la densidad de estados y el acoplamiento dependiente de la frecuencia

\[\tilde{C}_{e g}(\omega)=\omega^{2} D(\omega) W(\omega)(\bar{n}+1) \quad(\omega>0) \label{13.106}\]

\[\tilde{C}_{e g}(\omega)=\omega^{2} D(\omega) W(\omega) \bar{n} \quad(\omega<0) \label{13.107}\]

Se trata de un espectro de acción que refleja la densidad ponderada de acoplamiento de estados del baño que contribuye al espectro.

En la práctica, la inusualmente simetría de\(\tilde {C} _ {e g} ( \omega )\) y su crecimiento\(\omega^{2}\) hacen difícil trabajar con él. Por lo tanto, elegimos expresar la representación en el dominio de frecuencia de la densidad ponderada por acoplamiento de estados en la Ecuación\ ref {13.106} como una densidad espectral, definida como

\[\left.\begin{aligned} \rho ( \omega ) & \equiv \frac {\tilde {C} _ {e g}^{\prime \prime} ( \omega )} {\pi \omega^{2}} \\ & = \frac {1} {\pi} \int d \omega _ {\alpha} W \left( \omega _ {\alpha} \right) D \left( \omega _ {\alpha} \right) \delta \left( \omega - \omega _ {\alpha} \right) \\ & = \frac {1} {\pi} W ( \omega ) D ( \omega ) \end{aligned} \right. \label{13.108}\]

Esta expresión es real y se define sólo para frecuencias positivas. Note\(\tilde {C} _ {e g}^{\prime \prime} ( \omega )\) es una función impar en\(\infty\), y por lo tanto también lo\(\rho(\infty)\) es.

Ejemplo de densidad espectral usando una densidad óhmica de estados,\(W ( \omega ) = \omega \exp \left[ - \omega / \omega _ {C} \right]\) y un acoplamiento dependiente de frecuencia linealmente variable.

La energía de reorganización se puede obtener desde el primer momento de la densidad espectral

\[\lambda = \hbar \int _ {0}^{\infty} d \omega \omega \rho ( \omega ) \label{13.109}\]

Además, a partir de la ecuación\ ref {13.69} y\ ref {13.105} obtenemos la función lineshape en dos formas

\[\left.\begin{aligned} g (t) & = \int _ {- \infty}^{+ \infty} d \omega \frac {1} {2 \pi} \frac {\tilde {C} _ {e g} ( \omega )} {\omega^{2}} [ \exp ( - i \omega t ) + i \omega t - 1 ] \\[4pt] & = - \frac {i \lambda t} {\hbar} + \int _ {0}^{\infty} d \omega \rho ( \omega ) \left[ \operatorname {coth} \left( \frac {\beta \hbar \omega} {2} \right) ( 1 - \cos \omega t ) + i \sin \omega t \right] \end{aligned} \right. \label{13.110}\]

En esta expresión la dependencia de la temperatura implica que en el límite de temperatura alta,\(g(t)\) dominará la parte real de, como se esperaba para un sistema clásico. Esta es una expresión perfectamente general para la función lineshape en términos de una distribución espectral arbitraria que describe la escala de tiempo y la amplitud de las fluctuaciones de la brecha de energía. Dada una densidad espectral\(\rho(\infty)\), puede calcular varios observables espectroscópicos y otros procesos dependientes del tiempo en un entorno fluctuante.

Ahora, evaluemos el comportamiento de la función lineshape y absorción lineshape para diferentes formas de la densidad espectral. Para que las cosas sean simples, consideraremos el límite de temperatura alta,\(k _ {B} T \ll \hbar \omega\). Aquí

\[\operatorname {coth} ( \beta \hbar \omega / 2 ) \rightarrow 2 / \beta \hbar \omega\]

y podemos descuidar la parte imaginaria de la función de correlación de frecuencia y la función de forma de línea. Estos ejemplos están motivados por las densidades espectrales observadas para procesos aleatorios o ruidosos. Dependiendo del rango de frecuencia y proceso de interés, el ruido tiende a escalar como\(U \approx Z^{-n}\), dónde\(n = 0\),\(1\) o\(2\). Este comportamiento a menudo se describe en términos de una densidad espectral de la forma

\[\rho ( \omega ) \propto \omega _ {c}^{1 - s} \omega^{s - 2} e^{- \omega / \omega _ {c}} \label{13.111}\]

donde\(Z_c\) es una frecuencia de corte, y las unidades son frecuencia inversa. Estas densidades espectrales tienen la propiedad deseada de ser una función impar en\(Z\), y pueden integrarse a un valor finito. El caso\(s = 1\) se conoce como densidad espectral óhmica, mientras que\(s > 1\) es superóhmico y\(s < 1\) subóhmico.

Paso 1

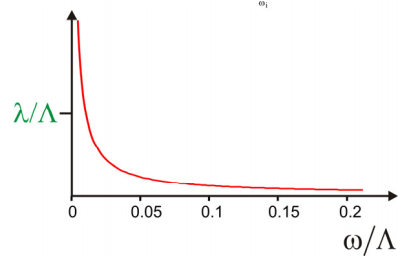
Consideremos primero el ejemplo cuando\(U\) cae como\(1/Z\) con frecuencia, que se refiere a la densidad espectral óhmica con una alta frecuencia de corte. Esta es la densidad espectral que corresponde a una función de correlación de brecha de energía que decae infinitamente rápido:\(C_{e g}(t) \sim \delta(t)\). Para elegir una definición consistente con la ecuación\ ref {13.109}, establecemos

\[\rho ( \omega ) = \lambda / \Lambda \hbar \omega \label{13.112}\]

donde\(\Lambda\) es un límite finito de integración de alta frecuencia que aplicamos para mantener\(U\) bien comportado. \(\Lambda\)tiene unidades de frecuencia, se equipara con el tiempo de correlación inversa para el decaimiento rápido de\(C_{eg}(t)\).

Ahora evaluamos

\[\begin{aligned} g (t) & = \int _ {0}^{\infty} d \omega \frac {2 k _ {B} T} {\Lambda \hbar \omega} \rho ( \omega ) ( 1 - \cos \omega t ) - \frac {i \lambda t} {\hbar} \\ & = \int _ {0}^{\infty} d \omega \frac {2 \lambda k _ {B} T ( 1 - \cos \omega t )} {\omega^{2}} - \frac {i \lambda t} {\hbar} \\ & = \lambda \frac {\pi k _ {B} T} {\Lambda \hbar^{2}} t - \frac {i \lambda t} {\hbar} \end{aligned} \label{13.113}\]

Luego obtenemos la función de desfase

\[F (t) = e^{- \Gamma t} \label{13.114}\]

donde hemos definido la constante de amortiguación exponencial como

\[\Gamma = \lambda \frac {\pi k T} {\Lambda \hbar^{2}} \label{13.115}\]

De esto obtenemos el lineshape de absorción

\[\sigma _ {a b s} \propto \frac {\left| \mu _ {e g} \right|^{2}} {\left( \omega - \omega _ {e g} \right) + i \Gamma} \label{13.116}\]

Así, una densidad espectral que escala como\(1 / \omega\) tiene un baño rápidamente fluctuante y conduce a un lineshape lorentziano homogéneo con un ancho medio\(\Gamma\).

Paso 2

Ahora tomemos el caso de que elegimos una densidad espectral lorentziana centrada en\(Z= 0\). Para mantener la función impar adecuada de\(Z\) y definición de\(O\) escribimos:

\[\rho ( \omega ) = \frac {\lambda} {\hbar \omega} \frac {\Lambda} {\omega^{2} + \Lambda^{2}} \label{13.117}\]

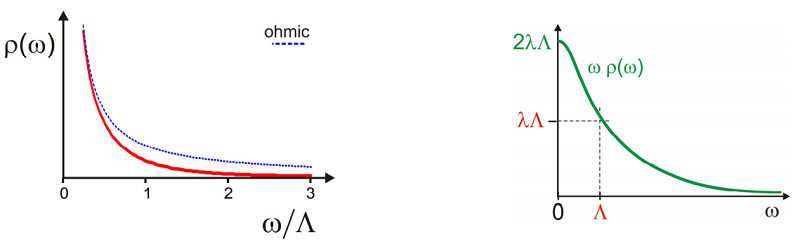
Tenga en cuenta que para frecuencias\(\omega \ll \Lambda\) esta tiene la forma óhmica de la Ecuación\ ref {13.112}. Esta es una densidad espectral que corresponde a una función de correlación de brecha de energía que cae exponencialmente como\(C_{e g}(t) \sim \exp (-\Lambda t)\). Aquí, en el límite de alta temperatura (clásica)\(k T>>\hbar \Lambda\), descuidando la parte imaginaria, encontramos

\[g (t) \approx \frac {\pi \lambda k T} {\hbar^{2} \Lambda^{2}} [ \exp ( - \Lambda t ) + \Lambda t - 1 ] \label{13.118}\]

Esta expresión parece familiar. Si equiparamos

\[\Delta^{2} = \lambda \frac {\pi k T} {\hbar^{2}} \label{13.119}\]

y

\[\tau _ {c} = \frac {1} {\Lambda} \label{13.120}\]

obtenemos la misma función de lineshape que el modelo gaussiano-estocástico clásico:

\[g (t) = \Delta^{2} \tau _ {c}^{2} \left[ \exp \left( - t / \tau _ {c} \right) + t / \tau _ {c} - 1 \right] \label{13.121}\]

Entonces, la interacción de una transición electrónica con un baño armónico conduce a un ensanchamiento de línea que equivale a fluctuaciones aleatorias de la brecha de energía. Como señalamos anteriormente, para el límite homogéneo, nos encontramos\(\Gamma = \Delta^{2} \tau _ {c}\).

Lecturas

1. Mukamel, S., Principios de Espectroscopia Óptica No Lineal. Oxford University Press: Nueva York, 1995; Ch. 7 y Ch. 8.