4.2: Método del Operador de Proyección

En el capítulo 3, exploramos el comportamiento a largo plazo de las funciones de correlación de tiempo, y en la sección anterior, exploramos su comportamiento a corto plazo. Sin embargo, en última instancia estamos interesados en encontrar expresiones para las funciones de correlación de tiempo que se apliquen en todas las escalas de tiempo.

Hay muchas formas diferentes de abordar este problema. En principio, podríamos simplemente calcular la posición y velocidad de cada partícula en el sistema en todo momento. Entonces, cualquier otra variable de espacio de fase\(A(t)\) podría determinarse fácilmente. Sin embargo, esto claramente no es viable para sistemas macroscópicos, que contienen en el orden de partículas\(10^{23}\) individuales.

Otro enfoque, y el que exploraremos aquí, es considerar solo esa parte del sistema que nos importa y tratar a todo el resto como un baño estadístico. Esto se puede lograr usando técnicas de operador de proyección. Para entender este método, es útil considerar una analogía con un espacio vectorial tridimensional. Cualquier vector tridimensional puede proyectarse sobre un vector de interés para encontrar su componente en esa dirección. De manera similar, podemos proyectar la información de posición y velocidad para todo el sistema y tratar el resto como un baño estadístico.\(A(t)\)

Para ilustrar esta idea, deja\(A(t)\) ser la velocidad de una partícula browniana. Siempre podríamos calcular\(A(t)\) determinando las posiciones y velocidades de todas las partículas en el sistema. Sin embargo, esto llevaría mucho tiempo y generaría mucha información innecesaria. En cambio, podemos proyectar la velocidad del sistema sobre la velocidad de la partícula browniana y tratar el resto del sistema como un baño.

Ya hemos resuelto este problema para un caso específico: en el capítulo 1, se utilizó la ecuación de Langevin para describir la evolución de la velocidad de una partícula bajo la influencia de la fricción y una fuerza aleatoria. En esta sección, utilizaremos la técnica del operador de proyección para derivar la Ecuación de Langevin Generalizada. No obstante, primero necesitamos definir algunos términos.

Definiciones

1. El Operador de Proyección Dados los vectores de columna\(A\) y\(B\), la\(B\) proyección de\(A\) on viene dada por la expresión

\[\mathcal{P}_{A} B=\frac{\langle B \mid A\rangle}{\langle A \mid A\rangle} A\]

Por definición,

\[\mathcal{P}_{A}^{2}=\mathcal{P}_{A}\]

Para un sistema de equilibrio, el producto del operador es

\[\langle B \mid A\rangle=\operatorname{Tr} B A^{+} \rho_{e q}\]

o, en la representación del espacio de fase

\[\langle B \mid A\rangle=\int d \Gamma B(\Gamma) A^{+}(\Gamma) \rho_{e q}\]

De igual manera, podemos definir el operador ortogonal\(\mathcal{Q}=\mathcal{P}-1\), que se proyecta sobre un subespacio que es ortogonal a A. 2. Identidad del operador Si\(a\) y\(b\) son operadores, las siguientes son identidades

\[\begin{aligned} &\frac{1}{s-a-b}=\frac{1}{s-a}+\frac{1}{s-a-b} b \frac{1}{s+a} \\ &e^{(a+b) t}=e^{a t}+\int_{0}^{t} e^{(a+b)(t-\tau)} b e^{a \tau} d \tau \end{aligned}\]

4. El operador de Liouville La evolución temporal de un operador A en un sistema con el Hamiltoniano\(\mathcal{H}\) se encuentra utilizando el operador de Liouville\(\mathcal{L}\)

\[\frac{d A}{d t}=i \mathcal{L} A\]

El operador de Liouville es una forma especial de operador llamado “superoperador” porque actúa sobre otros operadores en lugar de sobre funciones. En mecánica cuántica, el operador de Liouville para un sistema con el hamiltoniano\(\mathcal{H}\) se define como

\[i \mathcal{L} A \equiv \frac{1}{i \hbar}[A, \mathcal{H}]\]

donde\([\ldots, \ldots]\) indica el conmutador. En el límite clásico como\(\hbar \rightarrow 0\), esto se convierte

\[i \mathcal{L} A \equiv i\{A, \mathcal{H}\}\]

donde\(\{\ldots, \ldots\}\) está el soporte de Poisson. Una propiedad importante de\(\mathcal{L}\) es que es hermitiana. Esta propiedad queda demostrada en la siguiente prueba

\[\begin{aligned} \langle\mathcal{L} A \mid B\rangle=\operatorname{Tr}\left([A, \mathcal{H}] B^{+} \rho\right) \\ =\operatorname{Tr}\left(A \mathcal{H B}^{+} \rho-\mathcal{H} A B^{+} \rho\right) \\ =\operatorname{Tr}\left(A \mathcal{H} B^{+} \rho-A B^{+} \mathcal{H} \rho\right) \\ =\operatorname{Tr} A\left[\mathcal{H}, B^{+}\right] \rho \\ =\operatorname{Tr} A[\mathcal{H}, B]^{+} \rho \\ =\langle A \mid \mathcal{H} B\rangle \end{aligned}\]

La Ecuación de Langevin Generalizada

La ecuación de Liouville

\[\frac{d}{d t} A(t)=i L A(t)\]

tiene la solución formal

\[A(t)=e^{i \mathcal{L t}} A(0)\]

A partir de esta ecuación queda claro que la función\(e^{i L t}\) actúa como propagador de tiempo de\(A\) desde un valor inicial\(A(0)\). Sin embargo, no es muy útil en esta forma. Utilizaremos el operador de proyección para reescribir esta ecuación de una forma más útil. Para simplificar la notación,\(A(t)\) se escribirá\(A\) a partir de ahora. Comienza por escribir la nueva ecuación de movimiento para\(A(t)\)

\[\frac{d A}{d t}=i \mathcal{L} e^{i \mathcal{L} t} A\]

Insertar la identidad,\(I=(\mathcal{P}+\mathcal{Q})\)

\[\frac{d A}{d t}=e^{i \mathcal{L t}}(\mathcal{P}+\mathcal{Q}) i \mathcal{L} A=e^{i \mathcal{L t}} P i \mathcal{L} A+e^{i \mathcal{L t}} \mathcal{Q} i \mathcal{L} A\]

Empezar por evaluar el primer término. Usando la definición del operador de proyección, podemos reescribir esto como

\[\begin{aligned} e^{i \mathcal{L t}} \operatorname{Pi\mathcal} A=e^{i \mathcal{L} t} \frac{\langle i \mathcal{L} A \mid A\rangle}{\langle A \mid A\rangle} A \\ =i \frac{\langle\mathcal{L} A \mid A\rangle}{\langle A \mid A\rangle} e^{i \mathcal{L t}} A \\ =i \Omega A(t) \end{aligned}\]

donde\(\Omega\) se llama la matriz de frecuencia y se define como

\[\Omega=\frac{\langle\mathcal{L} A \mid A\rangle}{\langle A \mid A\rangle}\]

Para evaluar el segundo término, necesitaremos reescribir el propagador del tiempo en términos de\(\mathcal{P}\) y\(\mathcal{Q}\). Comience insertando la identidad y, a continuación, reescriba la expresión usando la identidad del operador definida en la sección A.2, con\(a=-i \mathcal{Q L}, b=-i P \mathcal{L}\), y\((a+b)=-i \mathcal{L}\)

\[\begin{aligned} e^{i \mathcal{L} t} &=e^{i(\mathcal{P}+\mathcal{Q}) \mathcal{L} t} \\ &=e^{i \mathcal{Q} L t}+\int_{0}^{t} e^{i \mathcal{L}(t-\tau)} i P \mathcal{L} e^{i \mathcal{Q} L t} d \tau \end{aligned}\]

Ahora, aplique esta expansión a\(i \mathcal{Q L} A\)

\[e^{i \mathcal{L t}} i \mathcal{Q L} A=e^{i \mathcal{Q L t}} i \mathcal{Q L} A+\int_{0}^{t} e^{i \mathcal{L}(t-\tau)} i P \mathcal{L} e^{i \mathcal{Q L t}}(i \mathcal{Q L} A) d \tau\]

Para entender esta expresión, comience por examinar el primer término. El operador\(\mathcal{Q}\) proyecta el sistema en los grados de libertad solventes, que son ortogonales a\(A\). Sin embargo, nos interesa principalmente describir solo la propagación en la\(A\) dirección. Por lo tanto, este término da la fuerza aleatoria o ruido en el sistema, que vamos a denotar\(R(t)\)

\[R(t)=e^{i \mathcal{Q} L t} i \mathcal{Q L} A\]

donde\(R(0)=i \mathcal{Q L} A\) y\(e^{i \mathscr{\mathcal { L }} t}\) describe el tiempo de propagación de\(R(t)\). El segundo término en esta expresión describe la fricción en el sistema. Una cosa interesante a tener en cuenta es que la expresión for\(R(t)\) aparece en este término, lo que indica que la fricción y el ruido del sistema están relacionados. Esta relación se denomina teorema de fluctuación-disipación, y se dará más explícitamente más adelante. Usando la definición de\(R(t)\), podemos reescribir el segundo término en la expresión como

\[\int_{0}^{t} e^{i \mathcal{L}(t-\tau)} i P \mathcal{L} e^{i \mathcal{Q} \mathcal{L} t}(i \mathcal{Q} \mathcal{L} A) d \tau=\int_{0}^{t} e^{i \mathcal{L}(t-\tau)} i P \mathcal{L} R(t) d \tau\]

Luego, usa la definición del operador de proyección\(\mathcal{P}\) para escribir

\[\int_{0}^{t} e^{i \mathcal{L}(t-\tau)} \frac{\langle i \mathcal{L} R(t) \mid A\rangle}{\langle A \mid A\rangle} A d \tau\]

Dado que el término de ruido ya\(R(t)\) está proyectado en el espacio ortogonal, siempre podemos operar sobre él\(\mathcal{Q}\) sin cambiar su valor (recuérdalo para cualquier operador de proyección\(\mathcal{P}, \mathcal{P}^{2}=\mathcal{P}\))

\[\int_{0}^{t} e^{i \mathcal{L}(t-\tau)} \frac{\langle i \mathcal{L} Q R(t) \mid A\rangle}{\langle A \mid A\rangle} A d \tau\]

Luego, usa el hecho de que\(\mathcal{Q}\) y\(\mathcal{L}\) son ambos operadores hermitianos para reorganizar la expresión

\[-\int_{0}^{t} e^{i \mathcal{L}(t-\tau)} \frac{\langle R(t) \mid i \mathcal{Q} \mathcal{L} A\rangle}{\langle A \mid A\rangle} A d \tau\]

Por último, utilizar la definición\(R(0)=i \mathcal{Q L} A\) y\(e^{i \mathcal{L}(t-\tau)} A=A(t-\tau)\) escribir la expresión como

\[-\int_{0}^{t} \frac{\langle R(t) \mid R(0)\rangle}{\langle A \mid A\rangle} A(t-\tau) d \tau\]

Definir el núcleo de memoria\(\kappa(t)\) como

\[\kappa(t)=\frac{\langle R(t) \mid R(0)\rangle}{\langle A \mid A\rangle}\]

Este término da el teorema final de fluctuación-disipación. El segundo término puede entonces escribirse de manera simple

\[-\int_{0}^{t} \kappa(t) A(t-\tau) d \tau\]

Con todo esto en la mano, finalmente podemos escribir la ecuación completa de Langevin Generalizado

\[\frac{d A}{d t}=i \Omega A(t)-\int_{0}^{t} \kappa(t) A(t-\tau) d \tau+R(t)\]

donde la matriz de frecuencia es

\[\Omega=\frac{\langle\mathcal{L} A \mid A\rangle}{\langle A \mid A\rangle}\]

la fuerza aleatoria es

\[R(t)=e^{i \mathcal{Q L t}} i \mathcal{Q L} A\]

y el núcleo de memoria, que define el teorema de fluctuación-disipación, es

\[\kappa(t)=\frac{\langle R(t) \mid R(0)\rangle}{\langle A \mid A\rangle}\]

Echemos un vistazo más de cerca a la matriz de frecuencias y al kernel de memoria. Para problemas unidimensionales, la matriz de frecuencias se evaluará a cero. Para entender por qué, recuerda eso\(i \mathcal{L} A=\frac{d A}{d t}\). Esto nos permite reescribir el numerador de la matriz de frecuencia como\(\left\langle\frac{d A}{d t} \mid A\right\rangle\), que es simplemente la derivada de la función de correlación\(C(t)=\langle A(t) \mid A(0)\rangle\), evaluada a cero. Dado que todas las funciones de correlación son pares en el tiempo, la derivada a cero debe ser igual a cero. Esta regla se aplicará a todos los problemas que abordemos en esta sección.

Como se dijo anteriormente, la definición del núcleo de memoria relaciona la fluctuación, o ruido en el sistema, con la disipación de\(A\). El término de fluctuación\(\langle R(t) \mid R(0)\rangle\langle A \mid A\rangle^{-1}\),, será cero cuando el ruido en el sistema sea cero. Esto indica que en un sistema aislado sin ruido,\(A\) decaerá rápidamente a cero.

Aplicaciones de la GLE

1. GLE para el movimiento browniano En el capítulo 1, utilizamos la ecuación de Langevin para explorar el movimiento de una partícula browniana. Aquí, realizaremos el mismo análisis utilizando la ecuación de Langevin Generalizado. Recordemos que el movimiento browniano describe el movimiento discreto y aleatorio que se observa cuando una partícula grande se sumerge en un fluido de partículas más pequeñas. Queremos usar el GLE para describir la velocidad de la partícula grande sin tener que resolver el movimiento de todo el baño.

Comience por escribir el GLE para la velocidad de la partícula. Para este sistema, la matriz de frecuencia\(\Omega\) es cero, por lo que la GLE completa viene dada por

\[\frac{d v}{d t}=-\int_{0}^{t} \gamma(t-\tau) v(\tau) d \tau+\frac{f(t)}{m}\]

donde\(\gamma(t)\) representa el núcleo de memoria y\(\frac{f(t)}{m}=R(t)\) representa la fuerza aleatoria. Para este sistema, el kernel de memoria viene dado por

\[\gamma(t)=\frac{\langle f(t) \mid f(0)\rangle}{m^{2}\langle v \mid v\rangle}\]

El factor de normalización\(\langle v \mid v\rangle^{-1}\) es simplemente el valor promedio de la velocidad al cuadrado,\(\left\langle v^{2}\right\rangle=v_{o}^{2}=\)\(\frac{k_{B} T}{m}\). Por lo tanto podemos escribir esto como

\[\gamma(t)=\frac{\beta}{m}\langle f(t) \mid f(0)\rangle\]

donde\(\beta=k_{B} T^{-1}\). El coeficiente de fricción para el sistema viene dado por\(\xi(t)=m \gamma(t)\). Usando esto, podemos escribir la relación fluctuación-disipación

\[\xi(t)=\beta\langle f(t) \mid f(0)\rangle\]

Podemos usar el GLE para encontrar la función de autocorrelación de velocidad\(C(t)=\langle v(t) v(0)\rangle\) para la partícula browniana. Comience multiplicando el GLE por\(v(0)\) y tomando el promedio térmico.

\[\begin{aligned} \frac{d v}{d t} &=-\int_{0}^{t} \gamma(t-\tau) v(\tau) d \tau+\frac{f(t)}{m} \\ \frac{d v}{d t} v(0) &=-\int_{0}^{t} \gamma(t-\tau) v(\tau) v(0) d \tau+\frac{f(t)}{m} v(0) \\ \left\langle\frac{d v}{d t} v(0)\right\rangle &=-\int_{0}^{t} \gamma(t-\tau)\langle v(\tau) v(0)\rangle d \tau+\frac{v(0)}{m}\langle f(t)\rangle \\ \frac{d C(t)}{d t} &=-\int_{0}^{t} \gamma(t-\tau) C(\tau) d \tau \end{aligned}\]

Aquí hemos utilizado el hecho de que el promedio térmico sobre la fuerza aleatoria\(\langle f(t)\rangle=0\). Esto nos da la ecuación de movimiento para\(C(t)\), que se puede resolver usando la transformación de Laplace. La transformación de Laplace de esta ecuación da

\[s \hat{C}(s)+\hat{\gamma}(s) \hat{C}(s)=C(0)\]

Usando\(C(0)=\langle v(0) v(0)\rangle=v_{o}^{2}\) y reordenando, obtenemos la solución general transformada de Laplace para\(C(t)\)

\[C \hat{(s)}=\frac{v_{0}^{2}}{s+\hat{\gamma}(s)}\]

que se puede resolver para valores especificados de\(\gamma(t)\).

La solución transformada de Laplace para se\(C(t)\) puede utilizar para encontrar una ecuación para la constante de difusión\(D\). La relación Green-Kubo define la constante de difusión como

\[D=\int_{0}^{\infty} C(t) d \tau=\hat{C}(s=0)\]

Usando la solución que derivamos anteriormente

\[D=\frac{v_{0}^{2}}{\hat{\gamma}(0)}=\frac{k_{B} T}{m \hat{\gamma}(0)}\]

Esta es una forma generalizada de la relación de Einstein, que derivamos en el capítulo 1 para la partícula browniana.

La partícula browniana experimenta ruido blanco, que se puede modelar haciendo de la función de memoria una función delta\(\gamma(t)=\gamma_{o} \delta(t)\). Entonces el GLE simplifica a

\[\begin{aligned} \frac{d v}{d t} &=-\int_{0}^{t} \gamma_{o} \delta(t-\tau) v(\tau) d \tau+\frac{f(t)}{m} \\ &=-\gamma_{o} v(t)+\frac{f(t)}{m} \end{aligned}\]

que tiene la solución formal (capítulo 1)

\[v(t)=v(0) e^{-\gamma t}+\frac{1}{m} \int_{0}^{t} e^{-\gamma(t-\tau)} f(t) d \tau\]

y la función de correlación\(C(t)=C(0) e^{-\gamma t}\). Usando la función de memoria de ruido blanco, también podemos reproducir la relación de Einstein del capítulo 1. La transformación de Laplace de\(\gamma(t)=\gamma_{o} \delta(t)\) es\(\hat{\gamma}(s)=\gamma_{o}\). Sustituyendo esto\(\hat{\gamma}(0)\) en la Eq. (4.28) y usando el coeficiente de fricción\(\xi(t)=m \gamma_{o}\) da la relación familiar de Einstein

\[D=\frac{k_{B} T}{m \hat{\gamma}(0)}=\frac{k_{B} T}{\xi}\]

3. Memoria de decaimiento exponencial Además del núcleo de memoria de función delta, que da la dinámica de una partícula browniana, también podemos considerar un caso en el que la fricción tiene la misma fuerza general\(\gamma_{o}\) pero varía con el tiempo. Podemos modelar esto con el kernel de memoria de decaimiento exponencial

\[\gamma(t)=\gamma_{o} \alpha e^{-\alpha t}\]

Este kernel de memoria tiene la propiedad especial de que no importa el valor de\(\alpha\), la integral de la función siempre será igual\(\gamma_{o}\). En el límite como\(\alpha \rightarrow \infty\), esta función se acerca\(\gamma_{o} \delta\left(t^{+}\right)\).

La función de correlación para este kernel de memoria es relativamente fácil de encontrar porque la transformación de Laplace de una función de decaimiento exponencial está bien definida. Para el decaimiento exponencial\(\gamma(t)\) definido anteriormente, la transformada de Laplace es

\[\hat{\gamma}(t)=\frac{\gamma_{o} \alpha}{s+\alpha}\]

Por lo tanto, para resolver la función de correlación, solo necesitamos encontrar el valor de\(\gamma_{o}\). Esto se puede estimar usando la definición del kernel de memoria

\[\gamma(0)=\frac{\langle i \mathcal{Q L} v \mid i \mathcal{Q L} v\rangle}{m^{2}\left\langle v^{2}\right\rangle}\]

Aquí,\(i \mathcal{L} v=\frac{d v}{d t}\) es simplemente la aceleración. Usando la ley de Newton, podemos escribir\(i \mathcal{L} v=\frac{F}{m}=\frac{-1}{m} \frac{\partial U}{\partial x}\), que es el gradiente del potencial, o el componente no aleatorio de la fuerza. Armando todo, encontramos que el kernel de memoria evaluado a cero es

\[\gamma(0)=\frac{\left\langle\partial_{x}^{2} U\right\rangle}{m} \equiv \Omega_{o}^{2}\]

Esta es la curvatura promedio del potencial. Para un oscilador armónico, esta es simplemente la frecuencia promedio.

Ahora podemos usar la transformada de Laplace del núcleo de memoria de decaimiento exponencial para encontrar la función de correlación.

\[\hat{C}(0)=\frac{v_{o}^{2}}{s+\frac{\Omega_{o}^{2}}{s+\alpha}}=v_{o}^{2} \frac{s+\alpha}{s^{2}+s \alpha+\Omega_{o}^{2}}\]

Esto es relativamente fácil de resolver porque es cuadrático. Para generar las soluciones, encuentra los valores propios resolviendo la ecuación cuadrática\(s^{2}+s \alpha+\Omega_{o}^{2}[1]\). Esto da los resultados

\[\begin{aligned} \lambda_{\pm} &=-\frac{\alpha}{2} \pm \sqrt{\frac{\alpha-4 \Omega_{o}^{2}}{4}} \\ C(t) &=v_{o}^{2} \frac{1}{\lambda_{+}+\lambda_{-}}\left(e^{-\lambda+t}-e^{-\lambda_{-} t}\right) \end{aligned}\]

De esta solución surgen algunos resultados interesantes. Podemos ver que si\(\alpha<2 \Omega\), entonces\(\lambda_{\pm}\) son números complejos y\(C(t)\) se vuelve oscilatorio

\[C(t)=v_{o}^{2} \frac{1}{\lambda_{+}+\lambda_{-}}(\cos \Delta t)\]

Podemos examinar estos resultados para diferentes relaciones entre\(\alpha\) y\(\Omega_{o}\).

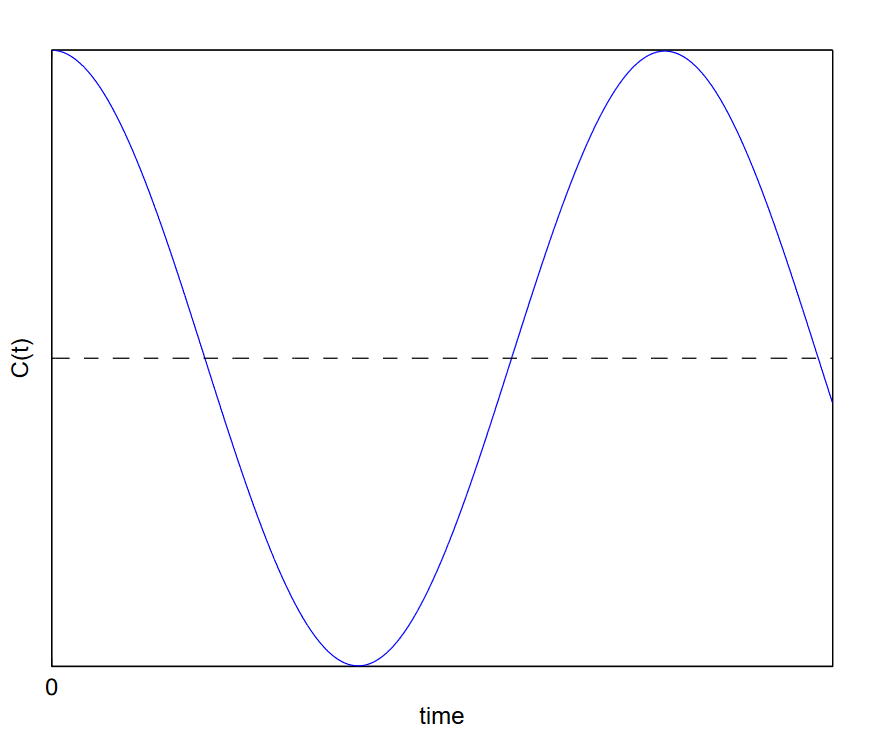
1. Sólidos Cuando\(\alpha \ll \Omega\), el tiempo de decaimiento es mucho más largo que un período de oscilación. La función de correlación muestra oscilaciones persistentes a muchas frecuencias. Prácticamente no hay amortiguación y el decaimiento se produce principalmente a través de la desfase (ver Figura 4.1).

Físicamente, esto representa un sólido. En un sólido, cada partícula individual se bloquea en su posición mediante una fuerte unión entre ella y sus vecinos. Si se altera desde el equilibrio, solo puede vibrar dentro del área pequeña permitida por estos enlaces.

Figura 4.1: Función de correlación de velocidad de un sólido

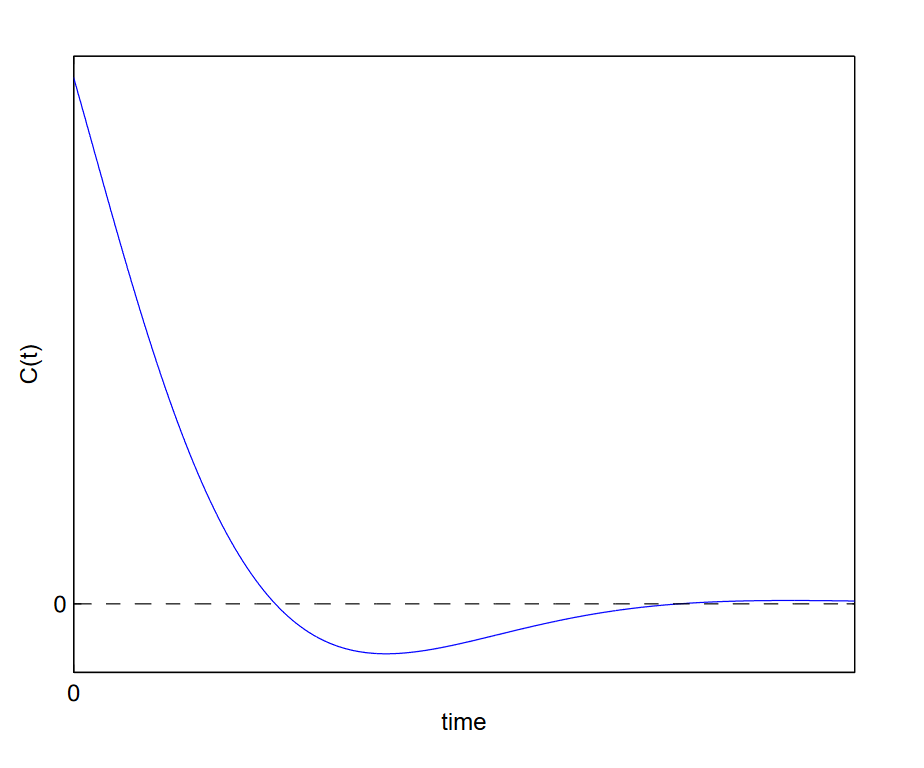
3. Líquidos Cuando\(\alpha l \Omega\), el tiempo de decaimiento es mayor que un período de oscilación. La función de correlación muestra una o dos oscilaciones que se amortiguan rápidamente y una cola de decaimiento de largo tiempo (Figura 4.2).

Físicamente, esto representa un líquido. En tiempos cortos, una molécula en un líquido es “atrapada” dentro de una cubierta de solvatación formada por enlaces intermoleculares débiles. Cuando se le perturba desde el equilibrio, inicialmente vibrará dentro de este caparazón. Sin embargo, en tiempos más largos, esta vibración provocará un reordenamiento de la cubierta de solvatación, permitiendo que la molécula se desplace lejos de su posición inicial. Esto humedece las oscilaciones.

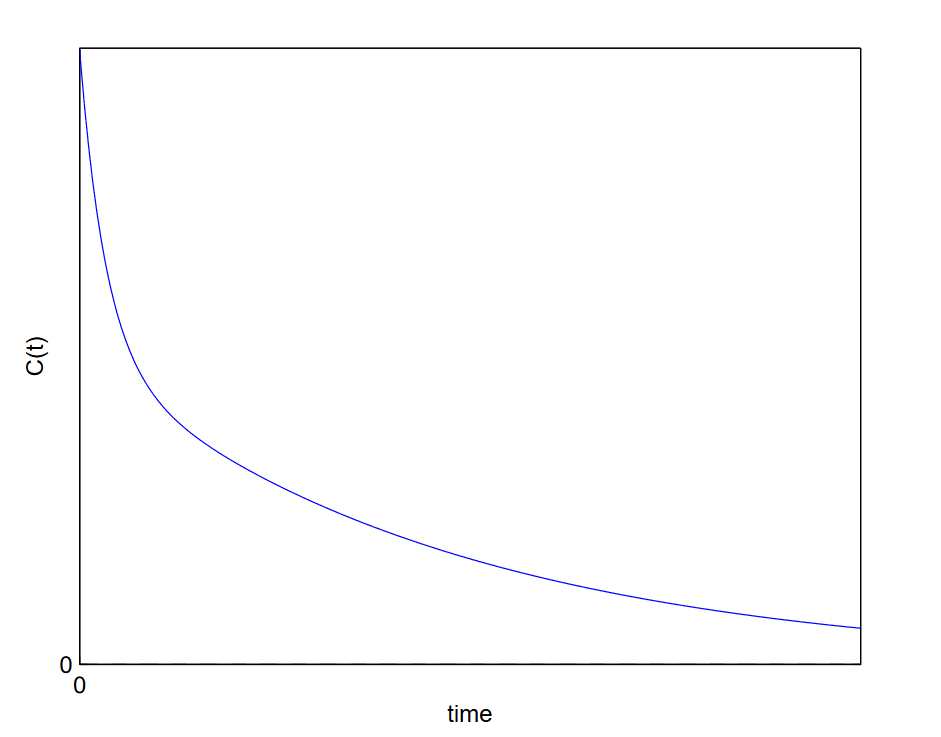
4. Gases Cuando\(\alpha \Omega\), el tiempo de decaimiento es menor que un periodo de oscilación. La función de correlación decae completamente antes de sufrir una oscilación (Figura 4.3).

Físicamente, esto representa un gas. En un gas, las moléculas no están confinadas por enlaces intermoleculares, y la función de correlación se desintegrará sin ninguna oscilación.

4. Constante de Difusión Generalizada Podemos utilizar la GLE para derivar la relación Verde-Kubo para la constante de difusión generalizada. Siguiendo un procedimiento similar al utilizado para la función de correlación de velocidad, podemos mostrar que se da la ecuación de movimiento para la función de dispersión intermedia (que hemos discutido en profundidad en el capítulo 3 y en la sección IC del capítulo 4)

Figura 4.2: Función de correlación de velocidad de un líquido

Figura 4.3: Función de correlación de velocidad de un gas

Sin embargo, este término es simplemente la constante de difusión\(D(\vec{k}, t)\) multiplicada por\(k^{2}\). Por lo tanto, la ecuación de movimiento para la función de dispersión intermedia se puede escribir como

\[\dot{F}(\vec{k}, t)=-k^{2} \int_{0}^{t} D(\vec{k}, \tau) F(\vec{k}, t-\tau) d \tau\]

En el límite de tiempo largo\(t \rightarrow \infty\) y el límite de longitud de onda larga\(k \rightarrow 0\), encontramos la relación Green-Kubo

\[D=\int_{0}^{\infty} D(0, t) d t=\int_{0}^{\infty} C(t) d t\]